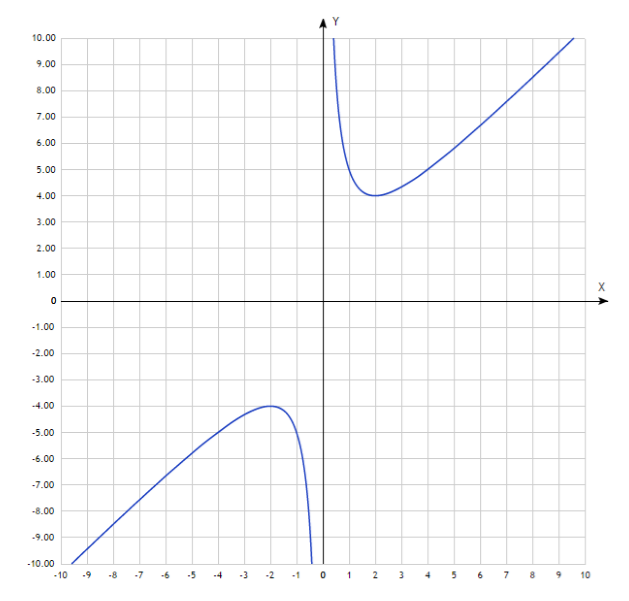
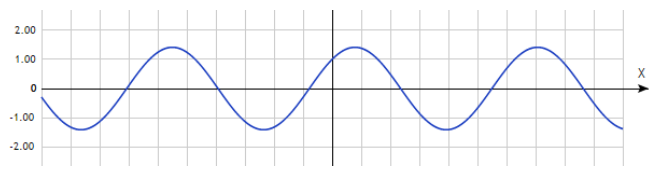
Четная функция симметрична относительно чего

Четные и нечетные функции

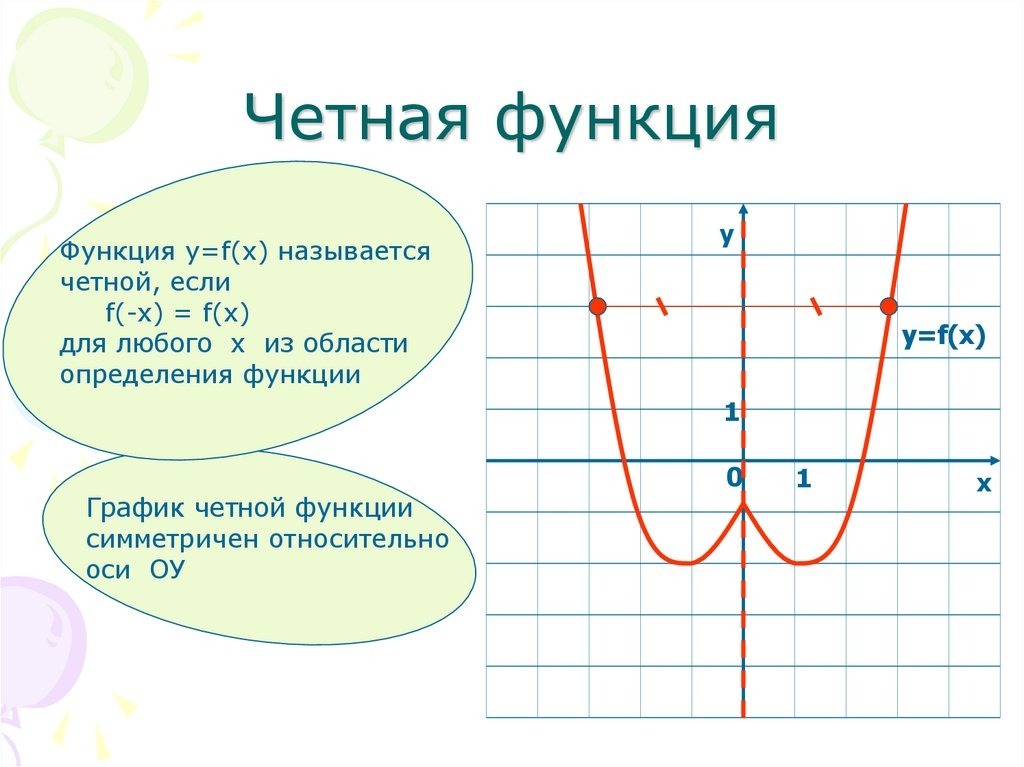
Функция называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

График четной функции симметричен относительно оси ординат.

Например, — четные функции.

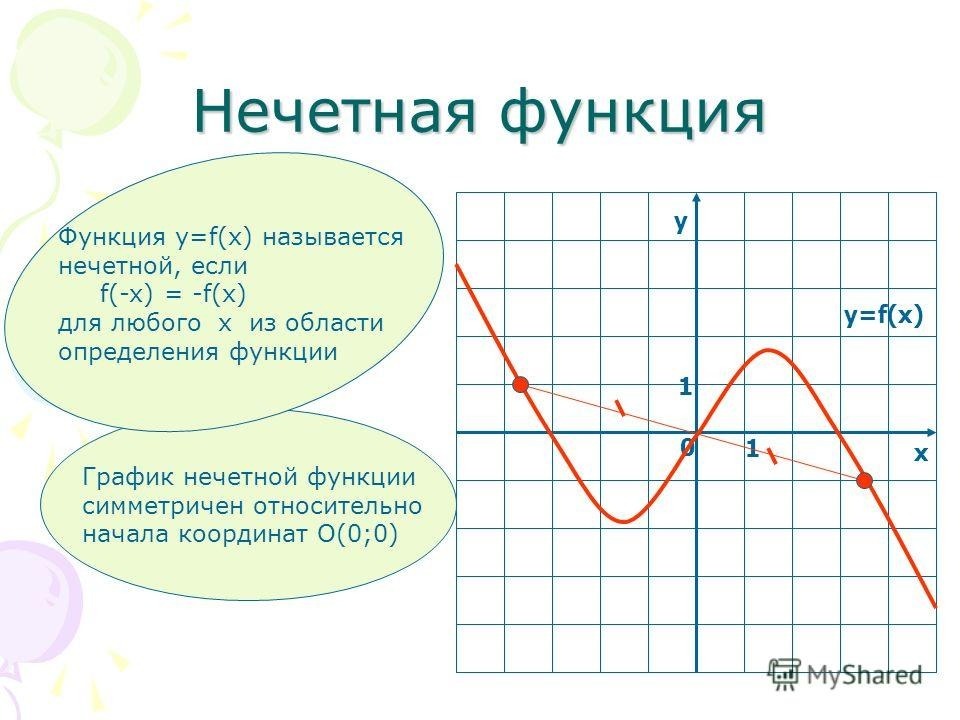
Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

График нечетной функции симметричен относительно начала координат.

Например, — нечетные функции.

Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.

Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:

1. Проверьте, является ли функция четной (нечетной).

Область определения функции

Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.

— значит, функция нечётная, её график симметричен относительно нуля.

2. Проверьте, является ли функция четной (нечетной)

Область определения: все действительные числа.

— чётная, как сумма двух чётных функций.

Её график симметричен относительно оси y.

3. Проверьте, является ли функция четной (нечетной).

Область определения функции симметрична относительно нуля.

— чётная, её график симметричен относительно оси y.

Источник

Понятие четной и нечетной функции

Понятие четности и нечетности функции

Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.

Четная функция

Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

График четной функции симметричен относительно оси Ох.

Нечетная функция

Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)

График нечетной функции симметричен относительно начала координат (точки (0;0)).

Произведение четной и нечетной функции

Произведение четной и нечетной функций есть нечетная функция.

Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)

Исследование функций в примерах

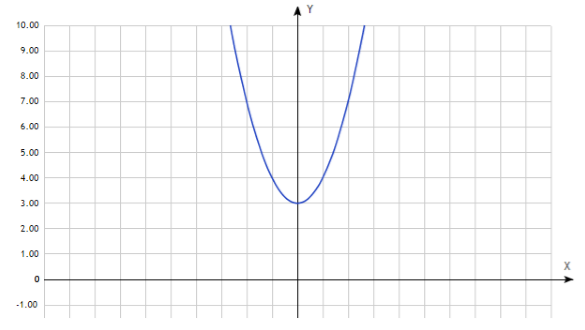
Доказать, что функция \(y=x^2\) четная.

1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.

Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)

1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.

Исследовать на четность и нечетность функции \(f_1(x)=\frac\) и \(f_2(x)=\frac4\)

Рассмотрим первую функцию:

1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.

Рассмотрим вторую функцию:

Источник

Четность и нечетность функции. Период функции. Экстремумы функции

Содержание

Способы задания функции

Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.

Четная и нечетная функция

Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.

Исследуем на четность нижеприведенную функцию:

Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.

Периодическая функция

f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty )

f(x) на (-\infty; x_ <1>) \cup (x_<2>; x_ <3>)

Ограниченность функции

Возрастающая и убывающая функция

Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0 ).

а) Если при x > 0 четная функция возрастает, то убывает она при x

б) Когда при x > 0 четная функция убывает, то возрастает она при x

в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x

Экстремумы функции

Необходимое условие

Достаточное условие

Наибольшее и наименьшее значение функции на промежутке

Источник

Четные и нечетные функции

Вы будете перенаправлены на Автор24

Четные функции

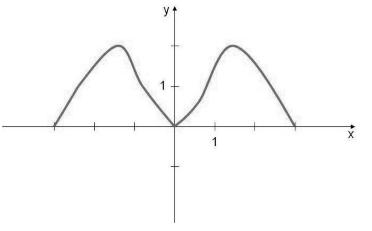
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).

Нечетные функции

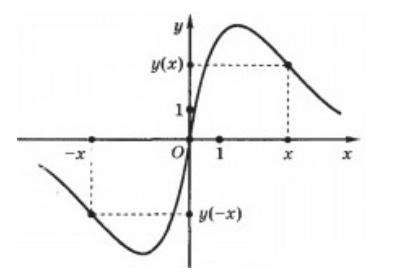
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).

Готовые работы на аналогичную тему

Функция общего вида

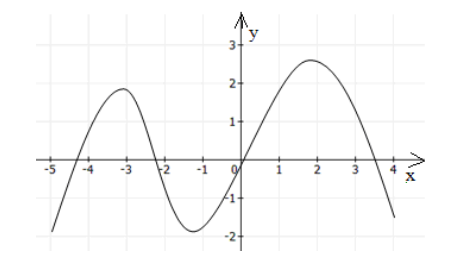
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.

Пример задачи

Исследовать функцию на четность и нечетность и построить их графики.

Изобразим её на графике:

Изобразим её на графике:

Изобразим её на графике:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 07 2021

Источник

Чётная функция

Чётная функция — это функция y=f(x), для любого значения x из области определения которой выполняется равенство:

В некоторых источниках условие симметрии области определения функции относительно нуля включают в определение чётной функции.

Чтобы доказать, что функция y=f(x) чётная, достаточно показать, что равенство f(-x)=f(x) выполняется при любых значениях x из области определения функции.

Доказать, что y=f(x) не является чётной функцией, можно двумя способами:

1) показать, что равенство f(-x)=f(x) не выполнено;

2) показать, что область определения y=f(x) не симметрична относительно нуля.

Примеры чётных функций:

Свойства чётных функций

1) График чётной функции симметричен относительно оси Oy.

Пусть y= f(x) — чётная функция.

Так как y= f(x) — чётная функция, то f(-a)=f(a)=b.

Значит, точка A1 (-a; b ) также принадлежит графику функции y= f(x).

Точки A (a; b) и A1 (-a; b) симметричны относительно оси Оy, то есть ось ординат является для графика функции y= f(x) осью симметрии.

Примеры графиков чётных функций — y=x², y=cos x, y=|х|.

2) Сумма, разность, произведение и частное чётных функций являются чётными функциями.

Пусть f(x) и g(x) — чётные функции, то есть f(-x)= f(x), g(-x)= g(x).

Определить, является ли функция чётной:

Условие y(-x)=y(x) выполнено. Следовательно, данная функция — чётная.

функция y=f(x) — чётная.

g(x) является чётной функцией.

данная функция не является чётной.

Функция не чётная, так как уё область определения — x∈ (-∞;1) и (1; ∞ ) не симметрична относительно точки x=0.

Источник