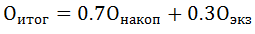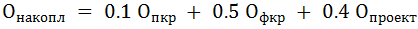Численные методы это что за предмет
Численные методы
Смотреть что такое «Численные методы» в других словарях:
численные методы — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN numerical methods … Справочник технического переводчика
Численные методы — Вычислительная математика раздел математики, включающий круг вопросов, связанных с производством вычислений и использованием компьютеров. В более узком понимании вычислительная математика теория численных методов решения типовых математических… … Википедия
Численные методы оптимизации — [numerical optimization technique] методы приближенного или точного решения математических задач оптимизации, сводящиеся к выполнению конечного числа элементарных операций над числами. (См. например, Градиентные методы). Численные методы предмет… … Экономико-математический словарь
численные методы оптимизации — Методы приближенного или точного решения математических задач оптимизации, сводящиеся к выполнению конечного числа элементарных операций над числами. (См. например, Градиентные методы). Численные методы предмет изучения вычислительной математики … Справочник технического переводчика
численные методы линейной алгебры — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN numerical linear algebra … Справочник технического переводчика
численные методы решения — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN numerical technique … Справочник технического переводчика
ГАЗОВОЙ ДИНАМИКИ ЧИСЛЕННЫЕ МЕТОДЫ — методы решения задач газовой динамики на основе вычислительных алгоритмов. Рассмотрим основные аспекты теории численных методов решения задач газовой динамики, записав газовой динамики уравнения в виде законов сохранения в инерциальной… … Математическая энциклопедия
Имитационные (численные) методы решения моделей — [numerical simulation methods] последовательное преобразование предварительно подготовленных численных значений исследуемых величин до получения искомого значения и его верификации. В частности, к ним относятся численные методы оптимизации. Ср.… … Экономико-математический словарь
имитационные (численные) методы решения моделей — Последовательное преобразование предварительно подготовленных численных значений исследуемых величин до получения искомого значения и его верификации. В частности, к ним относятся численные методы оптимизации. Ср. Аналитические методы решения… … Справочник технического переводчика
Для чего нужен предмет «Численные методы»?
Давайте, я попробую привести несколько примеров, которые сходу приходят на ум. Практически любое моделирование физических процессов заканчивается численными методами. Например моделлирование вихревых потоков в архитекруте или моделлирование воды в современных мультиках. Также в нескольки известных мне алгоритмах машинного зрения.
на этот вопрос сложно отвечать из-за его простоты. Примерно так же дети спрашивают для чего трава зеленая. Начинать им расказывать про фотосинтез?
Эти методы будут вами применяться во всех последующих дисцилинах. Например в оптимизации(неважно чего: процессов, движения или чего то еще, что можно описать уравнениями).
Примерно так же дети спрашивают для чего трава зеленая. Начинать им расказывать про фотосинтез?
думаю, полезно, когда у тебя есть какой-то дискретный сигнал и нужно его так или иначе обработать математически (не знаю как правильно выразиться)
вот однажды я пришел на собеседование и была такая задача
представим, что у нас есть некий девайс с акселерометром-гироскопами и наша задача как-нибудь примерно рассчитать изменение его координат в пространстве.
я не знаю правильного ответа, не уверен что он существует, но я думал так: у нас есть дискретные данные гироскопа/акселерометра, с каким-то шагом по времени, раз так, то мы можем проинтегрировать численно чтобы получить уравнение координаты. или можно построить полином какой-нибудь степени и проинтегрировать аналитически. вот тут как раз вступают в дело численные методы.
можно провести много параллелей с весьма полезными вещами 🙂
без вас бы я второстепенно относился бы к этому предмету.
Введение
Численные методы представляют собой отдельную область математики и применяются в различных прикладных направлениях. В частности, с помощью численных методов решаются и проблемы прикладной оптики. В данном пособии приводится обзор основных численных методов, чаще всего используемых при решении задач прикладной оптики. Особенностью пособия является использование в качестве заданий не просто математических функций, а реальных задач из области прикладной оптики, на примере которых рассматриваются численные методы. Это дает не только хорошее понимание сути самих численных методов, но и особенности их применения на практике.
Процесс решения любой сложной задачи, моделирования какого-то оптического процесса, можно представить как последовательность этапов.
Физическая постановка задачи. На этом этапе необходимо грамотно сформулировать и поставить задачу с точки зрения физики процесса. Для этого необходимо изучить рассматриваемую проблему и обладать знаниями в соответствующей области.
Математическая постановка задачи. На этом этапе нужно переформулировать физическую проблему на математический язык, то есть описывать в виде интегралов, систем уравнений, и т.д. Математическая модель должна корректно описывать основные законы физического процесса. В некоторых случаях на этом этапе можно остановиться, так как если задача простая, то существуют стандартные методы, которые нужно применить для решения этой задачи.
Метод непрерывной математики. На этом этапе оперируют не конечными числами, а функциями, общими величинами, то есть ищут решение проблемы в общем виде, и описывают при помощи математических формул.
Численные методы. Решение проблемы представляют в виде конечных математических операций – сложение, умножение. Численные методы позволяют свести решение задачи к выполнению конечного количества арифметических действий над числами, при этом результаты получаются в виде числовых значений. Чаще всего возможно использование известных стандартных численных методов.
Алгоритмизация. Алгоритмизация служит для упорядочения производимых действий в виде точного формального описания процесса. Алгоритм можно изобразить в виде блок-схемы или описать другим способом.
Программирование. На этом этапе алгоритм реализуется на каком-нибудь языке программирования высокого уровня.
Отладка программы. На этом этапе выполняется поиск ошибок, которые могли появиться на предыдущих этапах. Программа испытывается на решении тестовых задач для получения уверенности в достоверности результатов. Вполне вероятно, что придется вернуться в самое начало, к изменению физической постановки задачи, или какому-то другому этапу.
Проведение расчетов. На этом этапе готовятся исходные данные для расчетов, и проводятся вычисления по отлаженной программе.
Анализ результатов. Результаты расчетов анализируются, оформляется научно-техническая документация.
Все численные методы обладают некоторым набором характеристик. Наиболее важной из них является точность. На всех этапах решения задачи могут возникать погрешности, искажающие результаты вычислений, которые и определяют точность. Причины возникновения вычислительных погрешностей и способы их устранения рассматриваются в Приложении А.
При анализе точности одним из важнейших критериев является сходимость численного метода. Для дискретных методов (методы, которые заключаются в замене задачи с непрерывными функциями на задачу, в которой значения функций заданы в фиксированных точках) сходимость – это стремление значений решения метода к соответствующим значениям решения исходной задачи при стремлении к нулю параметра дискретизации (например, шага интегрирования).
Задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса ее решение существует, единственно и устойчиво. Применять для решения некорректно поставленных задач численные методы, не имеет смысла, поскольку возникающие в расчетах погрешности округления будут сильно возрастать в ходе вычислений, что приведет к значительному искажению результатов.
Устойчивость – это чувствительность метода к неточностям в исходных данных. Задача называется устойчивой, если малые погрешности в исходной величине приводят к малым погрешностям в решении. Отсутствие устойчивости означает, что даже незначительные погрешности в исходных данных приводят к большим погрешностям в решении или даже к неверному результату. О неустойчивых задачах также говорят, что они чувствительны к погрешностям исходных данных.
Таким образом, для получения решения задачи с необходимой точностью ее постановка должна быть корректной, а используемый численный метод должен обладать устойчивостью (корректностью) и сходимостью.
В большинстве случаев, кроме точности (сходимости, устойчивости, корректности) необходимо следить за минимизацией трудоемкости решения. Применительно к вычислительным задачам трудоемкость определяется объёмом памяти, используемым в процессе поиска решения, и временем, необходимым для выполнения вычислений. Время обычно измеряется в количестве элементарных операций (сложения, умножения, и т.д.), которые необходимо выполнить для решения задачи. Эти характеристики желательно уменьшать построением оптимальных алгоритмов вычисления, не потеряв при этом в точности. К сожалению, часто уменьшение трудоемкости и увеличение точности являются взаимоисключающими параметрами, и главной задачей является найти баланс между ними.
Численные методы
Вычислительная математика — раздел математики, включающий круг вопросов, связанных с производством вычислений и использованием компьютеров. В более узком понимании вычислительная математика — теория численных методов решения типовых математических задач.
К задачам вычислительной математики относят:
Основное отличие вычислительной математики заключается в том, что при решении вычислительных задач человек оперирует машинными числами, которые являются дискретной проекцией вещественных чисел на конкретную архитектуру компьютера. Так например если взять машинное число длиной в 8 байт, то в нём можно запомнить только 2 64 разных чисел, поэтому важную роль в вычислительной математике играют оценки точности алгоритмов и их устойчивость к представлениям машинных чисел в компьютере. Именно поэтому, например, для решения линейной системы алгебраических уравнений очень редко используется вычисление обратной матрицы, так как этот метод может привести к ошибочному решению в случае с сингулярной матрицей, а очень распространённый в линейной алгебре метод, основанный на вычислении определителя матрицы и её дополнения требует гораздо больше арифметических операций, чем любой устойчивый метод решения линейной системы уравнений.
Ссылки
Полезное
Смотреть что такое «Численные методы» в других словарях:
численные методы — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN numerical methods … Справочник технического переводчика
Численные методы — в математике, методы приближённого решения математических задач, сводящиеся к выполнению конечного числа элементарных операций над числами. В качестве элементарных операций фигурируют арифметические действия, выполняемые обычно… … Большая советская энциклопедия
Численные методы оптимизации — [numerical optimization technique] методы приближенного или точного решения математических задач оптимизации, сводящиеся к выполнению конечного числа элементарных операций над числами. (См. например, Градиентные методы). Численные методы предмет… … Экономико-математический словарь
численные методы оптимизации — Методы приближенного или точного решения математических задач оптимизации, сводящиеся к выполнению конечного числа элементарных операций над числами. (См. например, Градиентные методы). Численные методы предмет изучения вычислительной математики … Справочник технического переводчика
численные методы линейной алгебры — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN numerical linear algebra … Справочник технического переводчика
численные методы решения — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN numerical technique … Справочник технического переводчика
ГАЗОВОЙ ДИНАМИКИ ЧИСЛЕННЫЕ МЕТОДЫ — методы решения задач газовой динамики на основе вычислительных алгоритмов. Рассмотрим основные аспекты теории численных методов решения задач газовой динамики, записав газовой динамики уравнения в виде законов сохранения в инерциальной… … Математическая энциклопедия
Имитационные (численные) методы решения моделей — [numerical simulation methods] последовательное преобразование предварительно подготовленных численных значений исследуемых величин до получения искомого значения и его верификации. В частности, к ним относятся численные методы оптимизации. Ср.… … Экономико-математический словарь
имитационные (численные) методы решения моделей — Последовательное преобразование предварительно подготовленных численных значений исследуемых величин до получения искомого значения и его верификации. В частности, к ним относятся численные методы оптимизации. Ср. Аналитические методы решения… … Справочник технического переводчика
Численные методы в анализе данных
Содержание
О курсе
Этот курс численных методов похож на классическую вычислительную математику, но в то же время более практический. Студент на этой дисциплине научится владеть основными методами численного дифференцирования, интегрирования, интерполяции и аппроксимации, приближённо искать корни нелинейных уравнений и решать системы дифференциальных уравнений и многое другое. Будет рассказано о применении большинства алгоритмов в практических задачах показа медийной рекламы.
Курс читается с 2016 года.
Учебный план
Предусмотрены лекционные, семинарские занятия, 2 контрольных работы, а также курсовой проект.
Приблизительная программа лекций
Пример практической задачи: показ рекламы в сети Интернет (2 лекции, 2 семинара)
Общая схема процесса. Отличия от традиционной рекламы. Участники процесса. Медийная и контекстная реклама. Рекламные кампании, их параметры. Описание аудитории. Пространство сегментов аудитории. Вероятностное описание посетителей. Оценка профиля посетителя Интернета. Таргет рекламной кампании. Определение вероятности попадания посетителя в целевую аудиторию. Алгоритм показа медийной рекламы с таргетированием. Упрощенная модель показа рекламы с таргетированием в Интернете. Постановка практической задачи. Необходимость применения численных методов решения.
Предмет вычислительной математики (½ лекции)
Специфика машинных вычислений. Элементарная теория погрешностей.
Численное дифференцирование (½ лекции, 1 семинар)
Простейшие формулы численного дифференцирования. Оценка погрешности. Метод неопределенных коэффициентов вывода формул численного дифференцирования. Оптимальный шаг численного дифференцирования.
Приближение функций, заданных на дискретном множестве (2 лекции, 2 семинара)
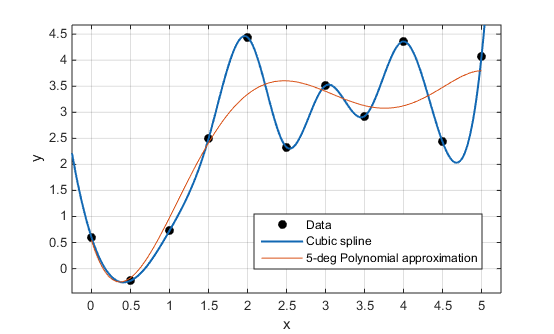
Задача алгебраической интерполяции. Существование и единственность алгебраического интерполяционного полинома. Интерполяционный полином в форме Лагранжа и в форме Ньютона. Остаточный член интерполяции. Интерполяция по чебышёвским узлам. Оценка погрешности интерполяции для функций, заданных с ошибками. Кусочно-многочленная интерполяция. Интерполяция сплайнами.
Численное интегрирование (1 лекция, 1 семинар)
Квадратурные формулы Ньютона-Котеса (прямоугольников, трапеций, Симпсона) и оценка их погрешности. Квадратурные формулы Гаусса.
Решение систем линейных алгебраических уравнений (4 лекции, 3 семинара)
Нормы в конечномерных пространствах. Обусловленность системы линейных алгебраических уравнений. Прямые методы решения: метод Гаусса, метод Гаусса с выбором главного элемента, метод прогонки для систем специального вида. LU-разложение и его связь с методом Гаусса. Итерационные методы решения линейных систем. Метод простых итераций. Необходимое, достаточное условия сходимости метода простых итераций. Методы Якоби, Зейделя. Методы решения, основанные на минимизации функционалов. Переопределенные системы линейных алгебраических уравнений.
Методы численного решения нелинейных уравнений (1 лекция, 1 семинар)
Принцип сжимающих отображений. Метод простых итераций. Условие сходимости метода простых итераций. Метод Ньютона. Порядок сходимости и условия достижения заданной точности итерационных методов. Метод релаксации.
Численные методы решения обыкновенных дифференциальных уравнений (2 лекции, 1 семинар)
Аппроксимация, устойчивость, сходимость. Теорема о связи аппроксимации, устойчивости, сходимости. Численные методы решения задачи Коши для ОДУ. Методы Рунге–Кутты и Адамса решения ОДУ. Численное решение краевых задач для ОДУ. Методы решения линейных и нелинейных краевых задач.
Применение численных методов в модели показа медийной рекламы (2 лекции, 2 семинара)
Применение численного интегрирования, табуляция результата. Использование интерполяции для вычисления функции, использование сплайнов. Численное решение системы линейных алгебраических уравнений для построения сплайна. Применение формул численного дифференцирования для аппроксимации уравнений. Численное решение задачи Коши для модели показа медийной рекламы. Имитационная модель системы показа медийной рекламы. Алгоритмы игры на аукционе RTB (Real-Time Bidding).
Курсовой проект
В курсовом проекте предлагается реализовать имитацию поведения рекламного сервера, описанного в виде системы дифференциальных уравнений. Особое творческое место занимает задача поиска оптимальной функции, влияющей на изменение порога показа рекламы. Подробное описание можно найти тут.
В курсовом проекте есть 4-5 промежуточных дедлайнов (сдаются ассистенту), к которым должны быть готовы определённые части программы и отчёта. За просроченный дедлайн максимальная итоговая оценка за проект снижается на 10%, подробнее тут. В конце предусмотрена итоговая защита проекта.
Активные дедлайны
Правила оценивания
Результирующая оценка по дисциплине рассчитывается по формуле
Накопленная и экзаменационная оценки округляются арифметически.
Накопленная оценка рассчитывается по формуле
Контакты
Канал в telegram для глобальных объявлений
Виктор Лобачёв, лекции и семинары
Александр Самохин, семинары
Марина Самохина, семинары
Максим Каледин, учебный ассистент
Полезные ссылки
Базовый учебник
Лобанов А.И., Петров И.Б. Лекции по вычислительной математике — М.: Интернет–Университет информационных технологий, 2006. — 522с.