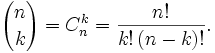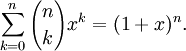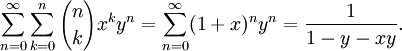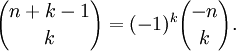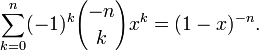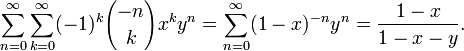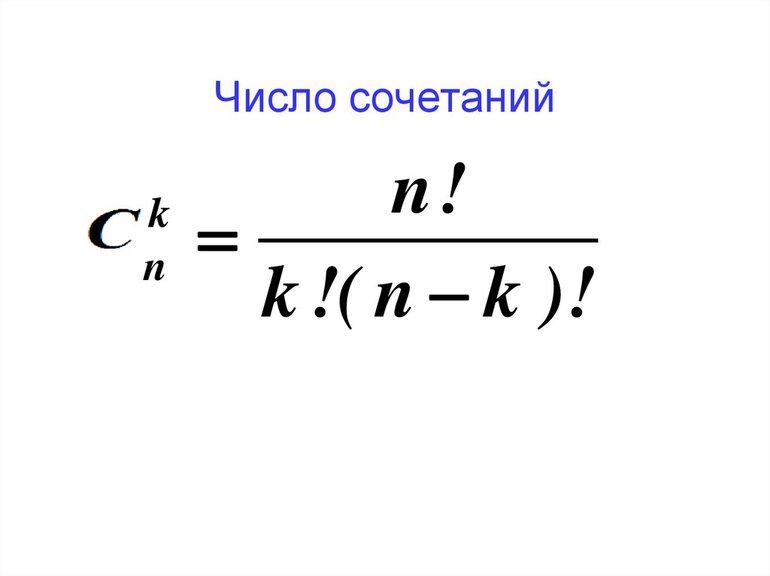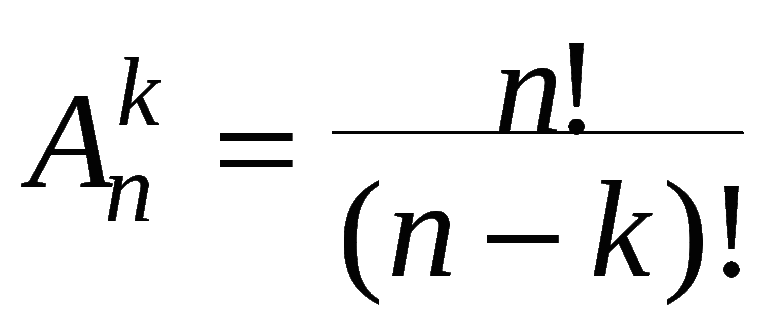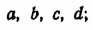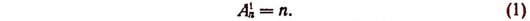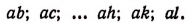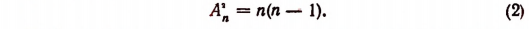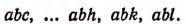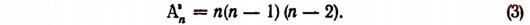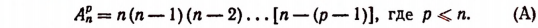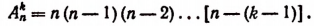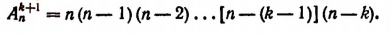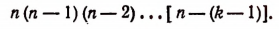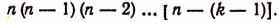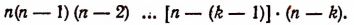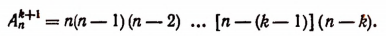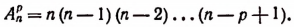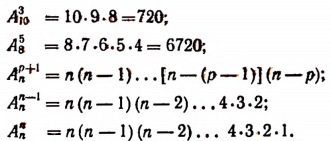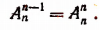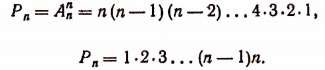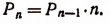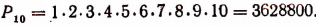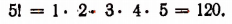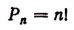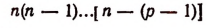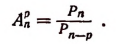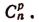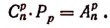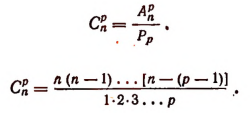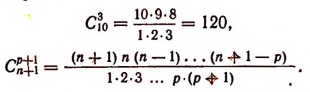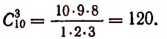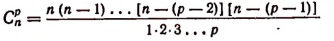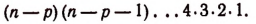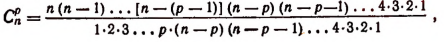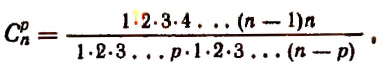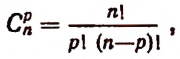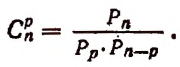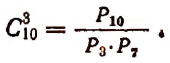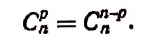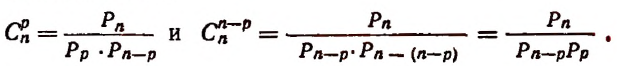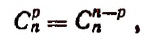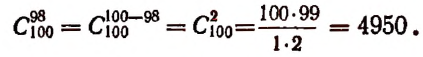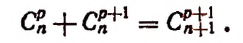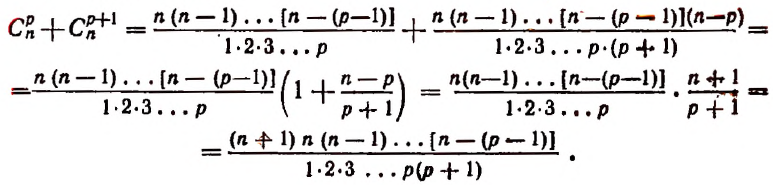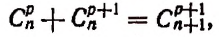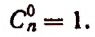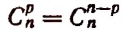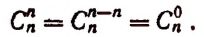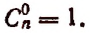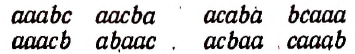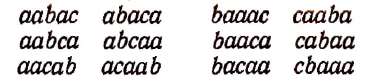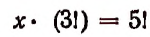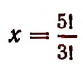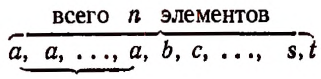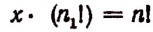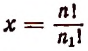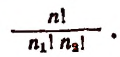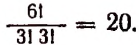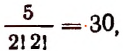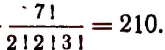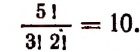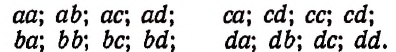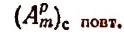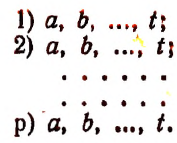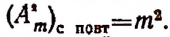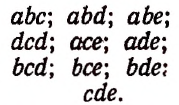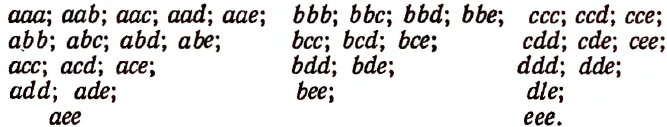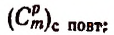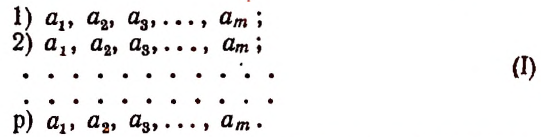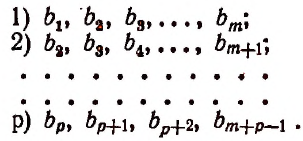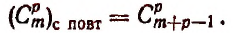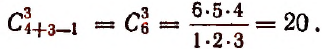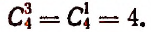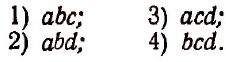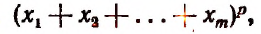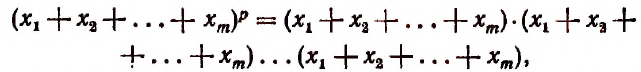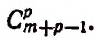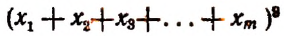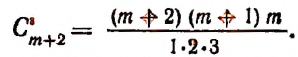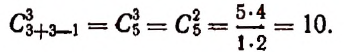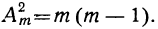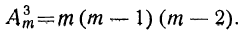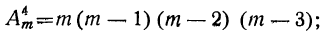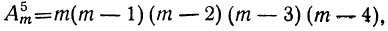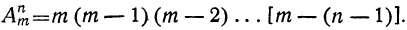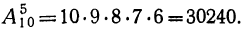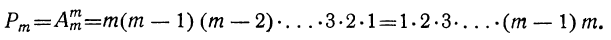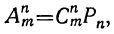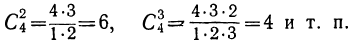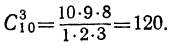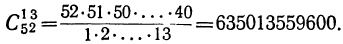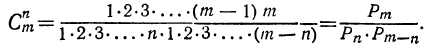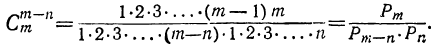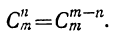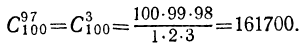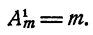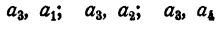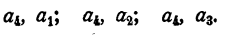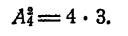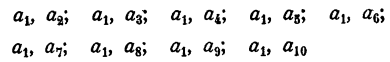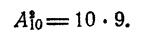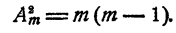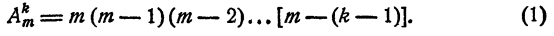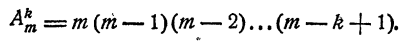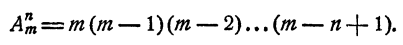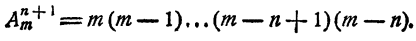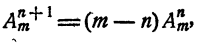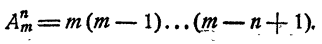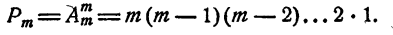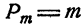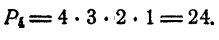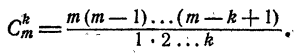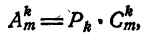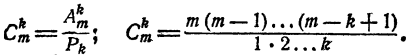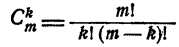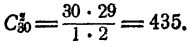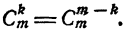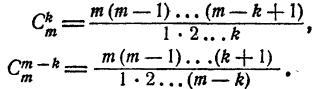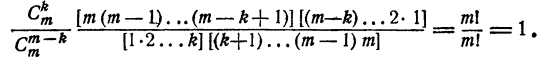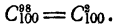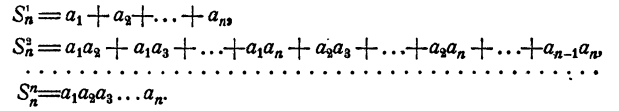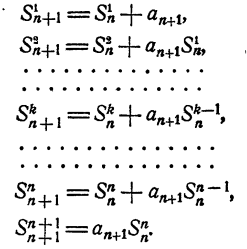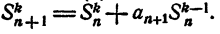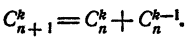Число сочетаний что это

Число сочетаний

Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Явные формулы

При фиксированном n производящей функцией последовательности чисел сочетаний , , , … является:

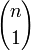
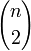
Двумерной производящей функцией чисел сочетаний является

Сочетания с повторениями

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.

Число сочетаний с повторениями из n по k равно биномиальному коэффициенту

При фиксированном значении n производящей функцией чисел сочетаний с повторениями из n по k является:

Двумерной производящей функцией чисел сочетаний с повторениями является:

Ссылки

Полезное

Смотреть что такое «Число сочетаний» в других словарях:

70 (число) — 70 семьдесят 67 · 68 · 69 · 70 · 71 · 72 · 73 40 · 50 · 60 · 70 · 80 · 90 · 100 Факторизация: 2×5×7 Римская запись: LXX Двоичное: 100 0110 … Википедия

ЭКСПОЗИЦИОННОЕ ЧИСЛО — световое число, условное число, однозначно выражающее внеш. условия при фотосъёмке (обычно яркость объекта съёмки и светочувствительность применяемого фотоматериала). Любому значению Э. ч. можно подобрать неск. сочетаний диафрагменное число… … Большой энциклопедический политехнический словарь

двойственное число — Форма числа, выделяющая два предмета как по отношению к единичному предмету, так и по отношению к множеству предметов. В современном русском языке эта форма не существует, но остатки ее влияния сохранились. Так, сочетания два стола (ср. мн. ч.… … Словарь лингвистических терминов

КОМБИНАТОРНЫЙ АНАЛИЗ — комбинаторная математика, комбинаторика, раздел математики, посвященный решению задач выбора и расположения элементов нек рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения… … Математическая энциклопедия

Сочетание — В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания… … Википедия

ВЕРОЯТНОСТЕЙ ТЕОРИЯ — занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера

Комбинаторика — 1) то же, что математический Комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов… … Большая советская энциклопедия

ПАРАДОКС — (греч. paradoxos неожиданный, странный) в широком смысле: утверждение, резко расходящееся с общепринятым, устоявшимся мнением, отрицание того, что представляется «безусловно правильным»; в более узком смысле два противоположных утверждения, для… … Философская энциклопедия

Формула включений-исключений — (или принцип включений исключений) комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом … Википедия

Комбинаторный анализ — математическая теория, занимающаяся определением числа различных способов распределения данных предметов в известном порядке; имеет особенно важное значение в теории уравнений и в теории вероятностей. Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Сочетания и размещения — что это такое и в чем разница

Оба этих понятия – сочетание и размещение – относятся к науке комбинаторике. Это раздел математики, созданный учеными Б. Паскалем и П. Ферма в процессе исследования теории карточных игр. Комбинаторика используется в решении задач особенного рода: когда требуется вычислить количество потенциальных вариантов для какой-либо ситуации. Примером может служить подсчет возможных позиций на шахматной доске после первого хода «черных» и «белых».

О сочетании и размещении говорят, когда из множества необходимо выбрать какое-либо подмножество. Понятия эти весьма близки по своему смыслу, поэтому так трудно бывает понять разницу между ними. Но она существует (причем принципиальная!). Ниже об этом достаточно простым языком написано в статье.

Сочетания

Сочетание – это подмножество, состоящее из К элементов, выбранных из множества, включающего в себя N элементов. При этом выполняется такое условие: N > К.

Важный момент: порядок расположения в данной выборке никакого значение не имеет. То есть комбинации, отличающиеся порядком размещения элементов, но не составом, считаются одинаковыми сочетаниями.

Образно проиллюстрировать понятие можно на примере лотереи. Предположим, человеку предлагается угадать 3 выпавшие цифры из 15-ти. Он выбрал следующий набор – 1, 6, 10. И уже не важно, в каком порядке они выпадут: 1, 6, 10; 1, 10, 6; 10, 1, 6; 10, 6, 1; 6, 10, 1; 6, 1, 10. Главное – состав комбинации. Если он совпадает с загаданным накануне набором цифр, игрок считается победителем.

Сочетания обозначаются следующим образом: С К _N. Где N – количество элементов в множестве, а К – количество объектов в производимой выборке. Для нашего примера N = 15, а К = 3.

Существует формула для определения числа возможных сочетаний в множестве. Выглядит она так: N!/((N-K)!*K!) подставим цифры из нашего примера:

Это означает, что из 15 чисел можно составить 455 различных комбинаций, включающих в себя три разных числа.

Такие подсчеты в нашем примере позволяют определить велики ли шансы субъекта на выигрыш.

Размещения

В самом названии этого термина присутствует корень, позволяющий понять его суть. Размещение – тоже подмножество, выбранное из первоначального множества. Но здесь уже существенное значение имеет место расположения элемента в комбинации. То есть если сочетания могут различаться только составом объектов, то размещения разнятся и составом, и порядком следования элементов.

Получается, что количество размещений всегда превосходит число сочетаний, при условии выборки из одного и того же множества.

Это легко проследить, если сделать выборку трех элементов из множества, состоящего всего из 4 объектов (от 1-го до 4-х).

Сочетаний здесь будет всего 4 (это легко проверить и по приведенной выше формуле):

Размещений же окажется гораздо больше:

123, 132, 321, 312, 231, 213, 234, 243, 324, 342 и т.д.

Существует формула, позволяющая подсчитать возможное количество размещений в представленном множестве:

Для нашего примера посчитаем количество потенциальных размещений:

Получается, что для состоящего из 4-х элементов множества существует 4 сочетания и целых 24 размещения.

Для тех, кто увлекается спортивными ставками, эти знания могут пригодится для того, чтобы рассчитать шансы на выигрыш.

Например, в турнире участвует 6 команд. Необходимо определить количество возможных комбинаций троек призеров кубка.

Обозначим названия команд буквами: А, Б, В, Г, Д, Е.

Сначала определим команду, которая станет золотым призером чемпионата. Таких вариантов, очевидно, 6: А, Б, В, Г, Д, Е.

Затем выбираем один из вариантов (пусть это будет комбинация, в которой золото принадлежит команде А), и определяем для него потенциального серебряного призера. Таких комбинаций уже окажется всего 5, так как одна команда уже записана на 1-м месте: АБ, АВ, АГ, АД, АЕ.

Такую пятерку вариаций можно сформировать для каждой из команд. То есть всего претендентов на серебро оказывается 30 (5*6).

Для каждой двойки первых призеров (чемпион-серебряный призер) можно составить только 4 комбинации с бронзовым призером. Первые два места уже распределены, так что остается 4 команды (6-2). Подберем комбинации для варианта АБ: АБВ, АБГ, АБД, АБЕ.

Мы уже подсчитали выше количество возможных комбинаций для первых двух мест – их оказалось 30. Теперь это число умножаем на 4 – получаем 120.

Выходит, что если в турнире участвует 6 команд, вариантов их размещения по первым трем местам может быть целых 120. Угадать призеров не так просто.

Сочетания и размещения: в чем же разница?

И сочетания, и размещения являются выборкой из определённого множества. Принципиальная разница между понятиями заключается лишь в том, что в случае сочетаний порядок расположения элементов не имеет значения, а в случае размещений он важен. Именно поэтому в пределах одного и того же множества количество сочетаний всегда оказывается меньше числа размещений.

Источник

Краткое описание

Изучение математических правил не может обойти стороной число сочетаний из n по k. Формулы комбинаторики как науки активно используются во всех жизненных отраслях. Этот раздел включён в школьную программу старших классов и вступительные испытания многих вузов России. Удивительная комбинаторика лежит в основе прикладного искусства.

Это направление науки начало активно развиваться ещё шесть веков назад. Достоверно известно, что первые комбинаторные задачи присутствовали в трудах философов и талантливых математиков Средневековья. В те времена представители стремительно развивающегося научного мира всячески пытались найти актуальные методы решения поставленных задач, хотели определить основные правила и понятия, а также утвердить уникальные в своём роде формулы и математические уравнения для тех, кто ещё не знаком с этим научным направлением.

Актуальные формулы и нормы комбинаторики применяются в распространённой теории вероятностей, где специалисты могут быстро и качественно подсчитать процент случайных событий, чтобы в итоге получить закон реального распределения случайных величин. При правильном подходе можно углублённо изучать закономерности тех или иных событий, что очень важно для понимания статистических природных правил, которые неизбежно проявляются в окружающей природе и эксплуатируемой технике.

Ключевые нюансы

Используемое в математике число сочетаний с повторениями можно подробно изучить по книгам и специальным изданиям. Комбинаторика подробно описана в том разделе науки, который занимается многофункциональными операциями с множеством задействованных элементов.

Экспертами было доказано, что это направление затрагивает довольно большой математический пласт, в котором ученикам предлагается изучить, сколько в мире существует различных комбинаций, подчиняющихся определённым условиям. Основной задачей этой науки можно считать требование размещения различных объектов по специальным правилам и последующее нахождение точного количества способов таких расположений.

На просторах интернета можно встретить много различных учебников и другого познавательного материала по информатике/математике для школьников, а также специальные сборники уравнений и сложных примеров для студентов, где в доступном и максимально подробном виде объяснена довольно увлекательная и познавательная комбинаторика. В начальных классах задачи на эту тему решают на специальных кружках, а вот в гимназиях с углублённым изучением точных наук ей посвящают основные уроки. Многоуровневые задачи по комбинаторике включены в программу олимпиады.

Существует ряд базовых понятий, которые нужно усвоить учащимся:

Необходимо отметить тот факт, что за основу может быть взят объект или целое явление, которое попадает в искомое множество. Перестановка затрагивает элементы, которые находятся в большом количестве и определённом порядке. Сочетание — своеобразные подмножества, пребывающие в произвольной форме. Размещение представляет собой упорядоченные подмножества в исходном множестве. Правильно посчитать нужный коэффициент можно при помощи многофункциональных онлайн-калькуляторов, которые обладают всеми необходимыми функциями.

Выборки и подсчёт суммы

Если предположить, что А = — множество из n элементов, то их совокупность будет называться выборкой объёма k из n. В этом случае действует ряд важных правил. Выборка может считаться правильно упорядоченной только в том случае, если итоговая последовательность следования всех задействованных элементов в ней была задана учеником заранее. Исключений не предусмотрено.

Различными выборками называются только те математические примеры, которые отличаются исключительно порядком следования элементов. Если отличия незначительные, тогда ученику предстоит работать с неупорядоченной комбинацией. В отдельных примерах могут допускаться или не должны допускаться повторения задействованных элементов.

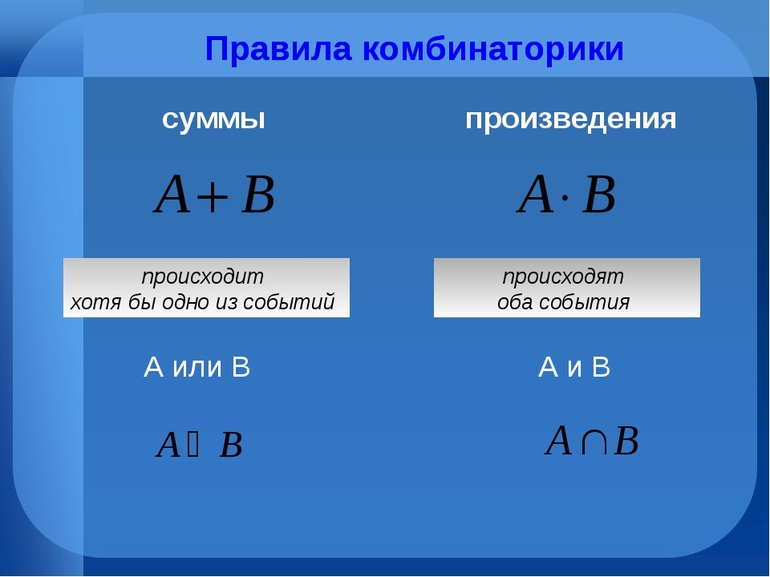
Чаще всего перед учащимися возникает необходимость подсчёта точного числа вероятных выборок с определёнными математическими параметрами. Довольно часто для контроля над вероятными комбинаторными объектами используется два ключевых приёма — правила произведения и суммы. На каждый случай специалисты предусмотрели ряд важных правил, которые призваны обезопасить учащегося от различных ошибок.

Базовое требование математического произведения основано на том, что когда исследуемый объект А может быть выбран различными f способами, то итоговый выбор А и B в указанном ранее порядке может быть осуществлён f * n методами. Правило суммы отличается тем, что если ученик имеет несколько возможностей выбрать точку А, тогда поиск А или В можно будет осуществить по специальной системе f + n.

Действующее правило произведения

Именно это направление в комбинаторике является одним из базовых для решения поставленных задач. При тщательном выборе элемента А из n способов (В из m) правильным считается то утверждение, в соответствии с которым одновременно подобрать пару А и В можно n * m методами, что очень важно. На этот случай действует три основных утверждения:

В эффективности описанных правил можно убедиться, благодаря некоторым примерам. По условиям задачи дано два ромба, три мяча, четыре гантели и пять кубов. Ученику нужно определить, сколькими способами можно будет вытянуть ромб, мяч, гантель и куб. Решение элементарное: 2*3*4*5= 120. Стоит отметить, что в этой задаче может быть задействован факториал, с помощью которого всегда можно вычислить более сложные варианты и решить трудные задачи.

По условиям следующего примера дано два мяча и пять скакалок. Задача состоит в том, чтобы определить, какова вероятность достать 1 скакалку и 1 мяч. Решение: 2*5=10.

Решение примеров комбинированного типа

Если ученик разобрался с основными свойствами сочетаний, то он также должен изучить уравнения всех доступных разновидностей задач с наиболее подходящими методами поиска правильных ответов. Эксперты рекомендуют потренироваться на более запутанных ситуациях, которые встречаются в повседневной жизни каждого человека. Основные категории задач:

Экспертами неоднократно было подтверждено, что комбинаторика является интересной и познавательной наукой, так как в наш век быстрой модернизации инновационных технологий постоянно будут нужны профессиональные специалисты, которые способны в полном объёме предоставить разнообразные решения для тех или иных практических задач.

Доступные размещения с повторениями и без них

Изучаемое число сочетаний без повторений сопряжено с некоторыми дополнительными нюансами. В этом случае в распоряжении учащегося имеется n разных математических элементов. Многих в такой ситуации интересует, сколько именно можно будет составить актуальных k расстановок.

Два базовых подхода считаются различными только при условии, если они отличаются друг от друга минимум одним элементом или состоят из аналогичных элементов, которые расположены в разном порядке. Каждый нюанс должен быть учтён, так как от этого зависит итоговый результат.

Источник

Соединения в комбинаторике с примерами решения и образцами выполнения

Группы, составленные из каких-либо предметов (безразлично какой природы, например букв, чисел, геометрических фигур, цветных флажков и т. п.), называются соединениями.

Сами предметы, из которых составляются соединения, называются элементами.

Различают три основных типа соединений: размещения, перестановки и сочетания.

Размещения

Пусть имеется п каких-либо различных элементов. Ради краткости обозначим их различными буквами:

а; b; с, …; h; k; l.

Определение:

Размещениями из п элементов по р в каждом называются такие соединения, из которых каждое содержит р элементов, взятых из числа данных п элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения.

Примеры:

Из одного элемента а можно составить лишь одно размещение.

Из двух элементов а и b можно составить два размещения по одному элементу и два размещения по два элемента ab, bа.

Из трех элементов а, b, с можно составить три размещения по одному элементу; шесть размещений по два элемента ab, ас, bа, be, са, cb; шесть размещений по три элемента abc, acb, bac, bca, cab, cba.

Из четырех элементов а, b, с, d можно составить 4 размещения по одному элементу:

12 размещений по два элемента:

ab, ас, ad; са, cb, cd;
ba, bc, bd; da, db, dc

24 размещения по три элемента:

abc, abd, acb, acd, adb, adc, bac, bad
bca, bcd, bda, bdc, cab, cad, cba, cbd
cda, cdb, dca, dcb, dba, dbc, dca, dcb

24 размещения по четыре элемента:

abcd, abdc, acbd, acdb, adbc, adcb, bacd, badc
bcad, bcda, bdac, bdca, cabd, cadb, cbad, cbda
cdab, cdba, dcab, dcba, dbac, dbca, dcab, dcba

По поводу размещений могут быть поставлены две основные задачи.

1. Имеется п элементов. Составить из них всевозможные размещения по р в каждом.

2. Имеется п элементов. Не составляя из них всевозможных размещений по р в каждом, определить, сколько таких различных размещений можно составить.

Начиная изложение теории размещений, мы не можем решить вторую задачу вне связи с первой. Но в дальнейшем, когда вторая задача будет решена в общем виде, мы уже не будем нуждаться в составлении самих размещений, а будем прямо подсчитывать число размещений в любом случае с помощью выведенного правила.

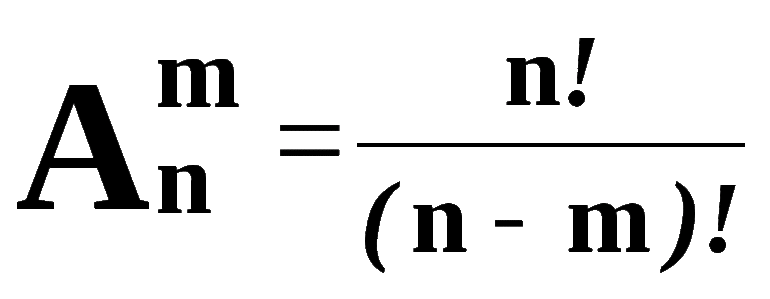
Число размещений из п элементов по р в каждом обозначается символом

Вывод формулы числа размещений

Пусть имеется п элементов а, b, с,…, h, k, l. Очевидно, что размещений из п элементов по одному будет п. Следовательно,

Чтобы определить число размещений из п элементов по два, сначала составим все такие размещения.

Воспользуемся уже имеющимися размещениями по одному:

а, b, с,…, h, k, l

Возьмем из этих размещений только первое, т. е. элемент а, и станем присоединять к нему по очереди каждый из остальных элементов. Тогда получим первую строчку размещений по два:

Поступая также с каждым из остальных размещений по одному, получим записанную ниже колонку всех размещений из n элементов по два:

Число размещений в каждой строке равно n — 1, а всех строк n. Следовательно,

Чтобы найти число размещений по три, воспользуемся уже имеющимися размещениями по два.

Возьмем из предыдущей колонки первое размещение по два и станем присоединять к нему по очереди каждый из (n — 2) оставшихся элементов. Тогда получим первую строчку размещений по три:

Поступая также с каждым из остальных размещений по два, получим записанную ниже колонку всех размещений из n элементов по три:

В каждой строке (n — 2) размещения, а всех строк n(n — 1). Следовательно,

Пользуясь методом математической индукции, можно доказать, что закономерность, наблюдаемая в формулах (1), (2) и (3), обладает общностью, т. е. доказать справедливость формулы

Допустим, что формула (А) справедлива при р = k, т. е. предположим справедливым следующее равенство:

Докажем, что в таком случае будет справедливым и равенство

Мы допустили, что число всех размещений из n элементов по k элементов равно произведению

Возьмем одно из этих размещений k-гo порядка и станем присоединять к нему по очереди каждый из оставшихся (п — k) элементов, не вошедших во взятое нами размещение. Тогда мы получим (п — k) размещений (k + 1)-го порядка.

Таким способом из каждого размещения k-гo порядка можно образовать (п — k) размещений (k + 1)-го порядка.

Но число всех размещений k-гo порядка по нашему предположению равно произведению

Следовательно, из всех размещений k-гo порядка можно составить указанным выше способом столько размещений (k + 1)-го порядка, сколько единиц окажется в произведении

Легко понять, что изложенным способом мы получим все размещения (k + 1)-го порядка, взятые только по одному разу. Поэтому окажется, что

Таким образом, из предположения, что формула (А) верна для р = k, мы пришли к тому, что эта формула оказалась верной и при р = k + 1. Но поскольку формула (А) верна, как это мы видели при р = 1, то, значит, она верна всегда, т. е. при любом натуральном значении р, меньшем или равном п.

Число множителей в правой части формулы (А) равно р. Эту формулу можно записывать и так:

Примеры:

Из последних двух формул следует, что

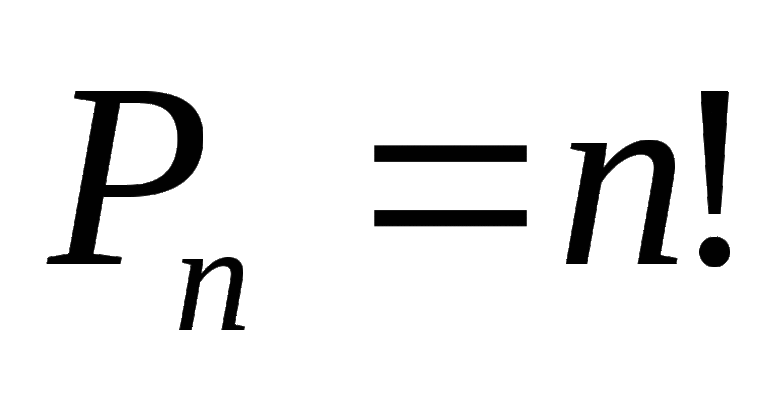
Перестановки

Определение:

Перестановками из п элементов называются такие соединения, из которых каждое содержит все п элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Число перестановок из одного элемента равно единице. Число перестановок из двух элементов a, b равно двум: ab; bа.

Число перестановок из трех элементов a, b, с равно шести: abc, acb; bac; bca; cab; cba.

Число перестановок из n элементов обозначается символом 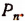Число перестановок из п элементов — это то же самое, что число размещений из п элементов по п в каждом. Поэтому

Число всех перестановок из п элементов равно произведению последовательных натуральных чисел от 1 до п включительно. Из формулы 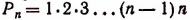следует, что

Примеры:

Отв.

Понятие факториала

Произведение я натуральных чисел от 1 до n обозначается сокращенно n!, т. е.

(читается n факториал).

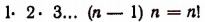
Выражение 5! читается: пять факториал.

2!= 2; 1! = 1.

Формулу числа перестановок теперь можно записать так:

Умножив и разделив произведение

Сочетания

Определение. Сочетаниями из п элементов по р в каждом называются такие соединения, из которых каждое содержит р элементов, взятых из числа данных п элементов, и которые отличаются друг от друга по крайней мере одним элементом.

Из одного элемента можно составить лишь одно сочетание. Из двух элементов а и b можно составить два сочетания по одному элементу а, b и лишь одно сочетание по два элемента ab.

Из трех элементов а, b, с можно составить: 3 сочетания по одному элементу:

3 сочетания по два элемента:

одно сочетание по три элемента:

Из четырех элементов а, b, с, d можно составить: 4 сочетания по одному элементу:

6 сочетаний по два элемента:

4 сочетания по три элемента:

одно сочетание по 4 элемента:

Соединение abc и соединение cab представляют собой одно и то же сочетание. Если же взять abc и abd или bcd, то это будут различные сочетания.

Число сочетаний из п элементов по р в каждом обозначается символом

Вывод формулы числа сочетаний

Если в каждом сочетании из п элементов по р сделать всевозможные перестановки, то образуются всевозможные размещения из п элементов по р. Поэтому

Заметим, что в выражении п (п—1)(n — 2)… каждый последующий множитель на единицу меньше предыдущего. Так, например.

Задача. Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов.

Отв.

Другой вид формулы числа сочетаний

Умножим числитель и знаменатель правой части формулы

Два основных свойства числа сочетаний

Первое свойство:

Доказательство:

что и требовалось доказать.

Пример:

Второе свойство:

Доказательство:

Но последнее выражение как раз и представляет собой 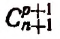. Поэтому

что и требовалось доказать.

Если воспользоваться формулой 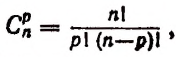то доказательство второго свойства можно изложить так:

Так, например,

Символ 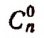не имеет смысла. Но в целях единообразной формы записи, с которой нам придется встречаться, мы примем по определению

При наличии этого определения мы можем формулу

применять и тогда, когда 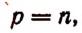т. е. писать

Эта запись будет правильной, так как

и

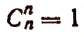
Аналогично этому принимают по определению

хотя символ 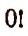сам по себе смысла не имеет.

Соединения с повторениями

Перестановки с повторениями

Пусть мы имеем 5 элементов, среди которых имеется три одинаковых элемента:

Перестановками из этих 5 элементов будут такие соединения, из которых каждое содержит все эти 5 элементов и которые будут отличаться друг от друга, следовательно, лишь порядком расположения Зтих пяти элементов.

Отсюда понятно, что элемент а будет входить в каждое соединение три раза.

Всевозможными перестановками из этих пяти элементов будут следующие:

Эти перестановки будут перестановками с повторениями потому, что в каждое соединение один и тот же элемент а входит три раза, т. е. столько раз, сколько раз он имелся среди данных пяти элементов.

Из написанной выше таблицы видно, что число перестановок из 5 элементов

т. е. перестановок с повторениями, равно 20.

Если же все 5 элементов были бы различными, то, как нам уже известно, число перестановок равнялось бы не 20, а числу 5!, т. е. 120.

Пусть мы не знаем число перестановок с повторениями из 5 элементов

Обозначим это неизвестное число буквой х. Теперь вообразим, что в группе а, а, а, b, с вместо трех одинаковых элементов а, а, а мы взяли три различных элемента 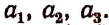Тогда имеющееся число перестановок х увеличится в 3! раза *. Но при этом число всех перестановок окажется равным числу перестановок из 5 различных элементов, т. е. будет равно числу 5! Таким образом,

Формула числа перестановок с повторениями

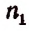
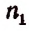
Пусть имеется п элементов, среди которых имеется одинаковых элементов.

одинаковых элементов

Число перестановок с повторениями из этих n элементов обозначим буквой х.

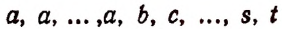
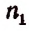
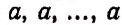
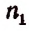
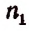
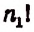
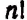
Теперь вообразим, что в группе вместо одинаковых элементов мы взяли различных элементов Тогда имеющееся число перестановок х увеличится во столько раз, сколько перестановок можно сделать из элементов, т. е. увеличится в раз. Но тогда число всех перестановок окажется равным числу перестановок из n различных элементов, т. е. будет равно числу . Поэтому

Если теперь рассматривать как одинаковые еще 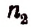элемента то число различных перестановок с повторениями из таких n элементов будет

Примеры:

Отв.

2. Различных перестановок букв можно сделать в слове;

замок — 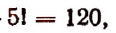ротор —

топор — 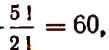колокол —

3. Я помню, что нужный мне телефонный адрес начинается с буквы К и содержит три «четверки» и две «пятерки». Однако расположение этих пяти цифр я позабыл. Спрашивается, сколько надо сделать проб, чтобы с гарантией связаться с нужным мне абонентом. (Предполагается, что на каждый телефонный вызов каждый вызываемый абонент будет отвечать при первом же его вызове.)

Из теории, изложенной выше, видно, что таких проб достаточно сделать

Размещения с повторениями

Сначала поясним на примере, какие соединения называются размещениями с повторениями.

Пусть имеется 4 различных элемента а, b, с, d и пусть требуется составить из этих 4-х элементов размещения с повторениями по два элемента.

Поскольку здесь речь идет о размещениях по два элемента, то, значит, каждое соединение, которое мы будем составлять, должно содержать по два элемента.

Если бы мы составляли размещения без повторений, то все элементы, входящие в любое размещение, обязательно должны были бы быть различными.

Например, размещениями без повторений из 4-х элементов а, b, c, d по два элемента были бы следующие:

Размещениями же с повторениями из этих 4-х элементов по два элемента будут следующие:

Размещение с повторениями из m элементов по элементов может содержать любой элемент сколько угодно раз от 1 до р включительно либо не содержать его вовсе.

Другими словами, каждое размещение с повторениями из m элементов по р элементов может состоять не только из р различных элементов, но из р каких угодно и как угодно повторяющихся элементов.

Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.

Число размещений с повторениями из m элементов по р элементов будем обозначать символом

Формула для числа размещений с повторениями

Пусть мы имеем сколько угодно комплектов m различных элементов:

Пусть теперь требуется узнать, сколько можно составить всевозможных размещений по р элементов с повторениями из различных элементов, если каждый из этих различных элементов имеется в нашем распоряжении в достаточном количестве.

Возьмем р комплектов данных m различных элементов:

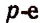
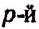
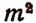
Поставим на первое место какой-либо элемент 1-й строки, на второе место, независимо от этого, какой-либо элемент 2-й строки н т. д. и, наконец, на место какой-либо элемент строки. Соединяя каждый элемент 1-й строки с каждым элементом 2-й строки, получим соединений по два, т. е.

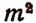
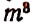
Присоединяя к каждому из этих соединений каждый элемент 3-й строки, получим соединений по 3 н т. д.

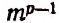
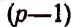
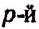
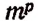
Присоединяя к каждому из соединений по каждый элемент строки, получим соединений по р.

Эти 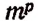соединений по р как раз и будут представлять всевозможные размещения по р элементов с повторениями из m различных элементов.

Примеры:

Отсюда видно, что на каждую из 10 букв — А, Б, В, Г, Д, Е, Ж, И, К, Л — приходится телефонных номеров 100 000. Следовательно, центральная телефонная станция г. Москвы может обслуживать непосредственно не более одного миллиона абонентов.

Сочетания с повторениями

Сначала поясним на примере, какие соединения называются сочетаниями с повторениями.

Пусть имеется 5 различных элементов а, b, с, d, е и пусть требуется составить из этих 5 элементов сочетания с повторениями по 3 элемента.

Поскольку здесь речь идет о сочетаниях по три элемента, то, значит, каждое соединение, которое мы будем составлять, должно содержать по три элемента и одно от другого должно отличаться по крайней мере одним элементом.

Если бы мы составляли сочетания без повторений, то все элементы, входящие в любое сочетание, обязательно должны были бы быть различными.

Например, сочетания без повторений из 5 элементов а, b, с, d, е по три элемента были бы следующие:

Сочетания же с повторениями из этих 5 элементов по три элемента будут следующими:

Сочетание с повторениями из m элементов по элементов может содержать любой элемент сколько угодно раз от 1 до р включительно, либо не содержать его вовсе.

Другими словами, каждое сочетание с повторениями из m элементов по р элементов может состоять не только из р различных элементов, но из р каких угодно и как угодно повторяющихся элементов.

Во всех случаях два соединения по р элементов не считаются различными сочетаниями, если они отличаются друг от друга только порядком расположения элементов.

Число сочетаний с повторениями из m элементов по р элементов будем обозначать символом

Формула числа сочетаний с повторениями

Чтобы составить всевозможные сочетания с повторениями из m различных элементов по р элементов, воспользуемся следующей таблицей:

Из первой строки возьмем какой-либо произвольный элемент; из второй строки возьмем элемент, расположенный либо непосредственно над взятым элементом из первой строки, либо справа от него; из третьей строки возьмем элемент, расположенный либо непосредственно над взятым элементом из второй строки, либо справа от него и т. д.

Совершив этот процесс с каждым элементом первой строки, мы получим всевозможные сочетания с повторениями из m различных элементов по р элементов.

Число всевозможных соединений, которые мы составили указанным выше способом, пользуясь таблицей (I), будет таким же, как если бы мы тем же способом стали бы составлять соединения, пользуясь следующей таблицей:

Но эти последние соединения представляли бы собой всевозможные сочетания без повторений из 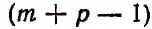различных элементов по р элементов.

Следовательно, число сочетаний с повторениями из m различных элементов по р элементов равно числу сочетаний без повторений из 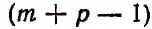различных элементов по р элементов, т. е.

Примеры:

Искомое число будет

Число же различных сочетаний из 4-х элементов а, b, с, d по 3 элемента без повторений равно

2. Найти число неподобных между собой членов разложения

получающихся после возведения в степень.

то искомое число будет равно числу сочетаний с повторениями из m различных элементов по р элементов, т. е. равно

В частности, в разложении

будет неподобных членов

В разложении 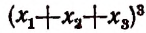неподобных членов будет

(Последний результат проверьте непосредственным возведением в куб многочлена )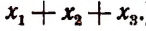

Что такое соединения и математика

Различные группы, составленные из каких-либо предметов и отличающиеся одна от другой или порядком этих предметов, или самими предметами, называются вообще соединениями.

Если, например, из 10 различных цифр: 0, 1, 2, 3, …, 9 будем составлять группы по нескольку цифр в каждой, например такие: 123, 312, 8056, 5630,42 и т. п., то будем получать различные соединения из этих цифр. Из них некоторые, например 123 и 312, различаются только порядком предметов, другие же, например 8056 и 312, разнятся входящими в них предметами (и даже числом предметов).

Соединения могут быть трёх родов: размещения, перестановки и сочетания. Рассмотрим их отдельно.

Размещения

Пусть число предметов, из которых мы составляем различные соединения, равно трём (например, 3 карты); обозначим эти предметы a, b и с. Из них можно составить соединения по одному:
а, b, с
по два:
ab, ас, be, ba, са, cb;
по три:
abc, acb, bас, bca, cab, cba.

Возьмём из этих соединений соединения по 2. Они отличаются одно от другого либо предметами, например ab и ас, либо порядком предметов, например ab и bа, но число предметов в них одно и то же. Такие соединения называются размещениями из трёх элементов по два.

Размещениями из m элементов по n называются такие соединения, из которых каждое содержит n элементов, взятых из данных m элементов, и которые отличаются одно от другого или элементами, или порядком элементов (значит, предполагается, что n ≤ m). Так, написанные выше соединения по 3 будут размещения из трёх элементов по 3 (различаются только порядком), соединения по 2 будут размещения из трёх элементов по 2 (различаются или предметами, или порядком).

Определим число всевозможных размещений, которые можно составить из m элементов по n, не составляя самих размещений. Число это принято обозначать так: 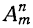(здесь А есть начальная буква французского слова „arrangement“, что значит „размещение“ ). Чтобы найти это число, рассмотрим приём, посредством которого можно составлять всевозможные размещения.

Так как всех элементов m, то из каждого размещения по одному элементу мы получим m — 1 размещений по 2, а всего их будет (m— 1)m. Очевидно, что других размещений по 2 быть не может. Значит:

Чтобы составить теперь размещения по 3, берём каждое из составленных сейчас размещений по 2 и приставляем к нему последовательно по одному все m — 2 оставшихся элементов. Тогда получим следующие размещения по 3:

Так как число всех размещений по 2 равно m (m — 1) и из каждого получается (m — 2) размещения по 3, то всех таких размещений окажется:
(m — 2) [m (m — l)]=m (m — 1) (m — 2).

Таким образом:

Подобно этому получим:


и вообще:

Такова формула числа размещений; её можно высказать так:

Число всевозможных размещений из m элементов по n равно произведению n последовательных целых чисел, из которых большее есть m.

Таким образом: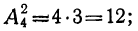
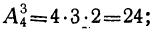
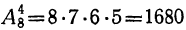
и т. п.

Задачи:

1) В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в день?

Всевозможные распределения уроков в день представляют собой, очевидно, всевозможные размещения из десяти элементов по 5; поэтому всех способов распределения должно быть:

2) Сколько можно образовать целых чисел, из которых каждое выражалось бы тремя различными значащими цифрами?

Искомое число есть число размещений из 9 значащих цифр по 3; следовательно, оно равно 9∙8∙7=504.

3) Сколько можно образовать целых чисел, из которых каждое изображалось бы тремя различными цифрами?

Из 10 цифр: 0, 1, 2, 3,…, 9 можно составить размещений по три 10∙9∙8=720; но из этого числа надо исключить число тех размещений по 3, которые начинаются с цифры 0. Таких размещений будет столько, сколько можно составить размещений по 2 из 9 значащих цифр, т. е. 9∙8=72; следовательно, искомое число 720 — 72=648.

Перестановки

Если размещения из m элементов взяты по m (т. е. различаются только порядком элементов), то такие размещения называются перестановками. Например, перестановки из двух элементов α, b будут размещения из 2 по 2, т. е. ab и bа, перестановки из трёх элементов а, b, с будут размещения из 3 по 3, т. е. abc, acb, bac, bca, cab, cba и т. п.

Так как перестановки из m элементов — это размещения из m по m, то формула числа перестановок будет такая:

Число всевозможных перестановок из m элементов равно произведению натуральных чисел от 1 до m.

Задачи:

1) Сколько девятизначных чисел можно написать девятью разными значащими цифрами?

Искомое число есть
P₉= 1∙2∙3∙4∙5∙6∙7∙8∙9=362880.

2) Сколькими способами можно разместить 12 лиц за столом, на котором поставлено 12 приборов?

Число способов равно:
1∙2∙3∙…∙ 12 = 479001600.

Замечание. Произведение натуральных чисел от 1 до m включительно (обозначается сокращённо так: m!) растёт чрезвычайно быстро с возрастанием m; так, при m = 12 оно даёт 479001600, при m= 100 оно выражается числом, требующим 158 цифр для своего изображения.

Сочетания

Если из всех размещений, которые можно составить из т элементов по n, мы отберём только те, которые одно от другого разнятся по крайней мере одним элементом, то получим соединения, которые называются сочетаниями.

Например, из четырёх элементов а, b, с и d сочетания по 3 будут:
abc, abd, acd, bcd.

Если в каждом из этих сочетаний сделаем всевозможные перестановки, то получим всевозможные размещения из четырёх элементов по 3:

Число таких размещений равно, очевидно, 6∙4=24.

Таким образом, число всех размещений из m элементов по n равно числу всех сочетаний из m элементов по n, умноженному на число всех перестановок, какие можно сделать из n элементов, т. е.

где 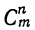означает число всех сочетаний из m по n (С есть начальная буква французского слова „combinaison», что значит „сочетание»).

Отсюда выводим следующую формулу числа сочетаний: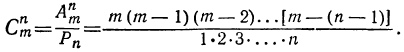

Например:

Примеры:

1) Из 10 кандидатов на одну и ту же должность должны быть выбраны трое. Сколько может быть разных случаев выборов?

Искомое число, очевидно, составляет число всевозможных сочетаний из десяти элементов по 3, т. е.

2) Сколькими способами можно выбрать 13 карт из колоды в 52 карты?

Искомое число представляет собой число сочетаний из 52 по 13, т. е.

Другой вид формулы числа сочетаний

Формулу числа сочетаний можно привести к другому виду, если умножим числитель и знаменатель её на произведение 1∙2∙3… (m — n); тогда в числителе получим произведение m (m — 1) … [m — (n — 1)]∙1 ∙2∙3∙ … ∙(m-n), которое, переставив сомножители, можно написать:
1∙2∙3∙ … ∙(m — n) [m — (n — 1)] … m.

Следовательно:

Свойство сочетаний

Заменив в этой формуле n на m — n, получим:

Сравнивая эту формулу с предыдущей, находим:

К этому выводу приводит и такое простое рассуждение: если из m элементов отберём какие-нибудь n элементов, чтобы составить из них одно сочетание, то совокупность оставшихся элементов составит одно сочетание из m — n элементов. Таким образом, каждому сочетанию из n элементов соответствует одно сочетание из m— n элементов, и наоборот; значит:

Это соотношение позволяет упростить нахождение числа сочетаний из m элементов по n, когда n превосходит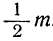. Например:

Соединения и Бином Ньютона

Размещения

Имеется m элементов (т. е. предметов, букв, цифр, чисел и т. д.). Выберем из них какие-нибудь k элементов (k ≤ m) и расположим эти k элементов в каком-нибудь порядке, т. е. так, чтобы было известно, какой элемент находится на первом месте, какой — на втором и т. д.

Определение:

Расположенная совокупность k элементов, взятых из данных m элементов, называется размещением из m элементов по k.

По определению, два размещения из т элементов по k являются различными, если они отличаются или самими элементами, или порядком их расположения.

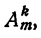
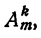
Число всевозможных размещений из т элементов по k обозначается знаком , где m показывает число всех элементов, a k — число элементов, входящих в каждое размещение. Задача состоит в отыскании общей формулы для подсчета . Решение задачи разобьем на две части. В первой части рассмотрим несколько частных случаев с тем, чтобы на основе их построить гипотезу для общего случая. Во второй части проверим гипотезу методом математической индукции.

содержащую еще три размещения. Далее имеем строку

Всего имеем 4 строки, в каждой из которых содержится три размещения из 4 элементов по 2. Таким образом,

Если бы m = 10, то, поступая таким же образом, мы получили бы 10 строк, в каждой из которых содержалось бы по 9 размещений из 10 элементов по 2:

и т. д. Таким образом,

Все это наводит на гипотезу, что при всяком m.

Рассматривая, если потребуется, еще и другие примеры, можно ваметить, что 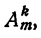равно произведению k последовательных целых чисел, наибольшее из которых m, т. е. при любом m и при любом k (конечно, k ≤ m)

Рассуждения, которые были проведены, не являются доказательством того, что формула (1) верна. Эти рассуждения дали лишь возможность построить гипотезу. Нужно еще доказать, что гипотеза эта верна.

Теорема:

Число размещений из m элементов по k может, быть вычислено по формуле

Доказательство:

Доказательство проводится методом математической индукции, причем индукция ведется по k

При k = 1 утверждение справедливо, так как непосредственно видно, что 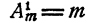и по формуле (1)

Допустим, что утверждение справедливо при k = n, где n

Докажем, что тогда утверждение должно быть справедливым и при k = n + 1, т. е.

Для получения размещений из от элементов по n + 1 возьмем все размещения из m элементов по n и к каждому из них на (n + 1)-е место припишем каждый из остальных n — m элементов. Таким путем получим 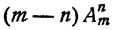размещений.

Если мы теперь докажем, что ни одно размещение из от элементов по n + 1 нами не пропущено и ни одно из этих размещений не выписано дважды, теорема будет доказана.

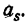
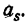
Возьмем произвольное размещение A из m элементов по n + 1. Пусть в размещении А на (n + 1)-м месте находится элемент . Отбросим этот элемент, получим размещение A₁ из m элементов по n. Так как мы брали все размещения из m элементов по n, взято и размещение A₁. К этому размещению на (n + 1)-е место мы приписывали каждый из остальных элементов, значит, приписали и элемент . Выходит, что ни одно размещение из m элементов по n + 1 нами не пропущено.

Допустим теперь, что размещение A из m элементов по n + 1 нами получено дважды. Вычеркнем в каждом из этих размещений элемент, находящийся на последнем месте. Получим одно и то же размещение A₁ из m элементов по n. Выходит, что к одному и тому же размещению A₁, два раза в конце был приписан один и тот же элемент, Это противоречит способу, посредством которого составлялись размещения из от элементов по n + 1.

Утверждение справедливо при k = 1, и из справедливости его при k = n следует его справедливость при k = n + 1.

Пример:

Пример:

Сколько различных двузначных чисел можно записать при помощи цифр 1, 2, 3 и 4, если ни одна цифра не входит в изображение числа дважды?

Решение:

Искомое число равно

Перестановки

Размещения из m элементов по m называются перестановками из от элементов. Таким образом, две различные перестановки из данных m элементов не могут отличаться одна от другой элементами, а отличаются только порядком расположения элементов.

Определение:

Расположенная совокупность m элементов называется перестановкой из m элементов.

Число всевозможных различных перестановок из m элементов обозначается знаком 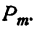. По определению,

Произведение 1.2…m первых m натуральных чисел обозначается m (читается: m факториал). Таким образом,

Пример:

Решение:

Искомое число равно числу всевозможных перестановок из четырех элементов

Сочетания

Определение. Сочетанием из m элементов по k называется совокупность, образованная любыми k элементами из данных m. Два сочетания из m элементов по k считаются различными тогда и только тогда, когда они отличаются по крайней мере одним элементом.

В отличие от размещений, где существенное значение имеет порядок, в котором расположены элементы, в сочетаниях порядок расположения элементов не имеет значения.

Число всевозможных сочетаний из m элементов по k обозначается знаком

Теорема:

Число всевозможных сочетаний из m элементов по k может быть вычислено по формуле

Доказательство:

Предположим, что мы составили таблицу всех сочетаний из m элементов по k. Назовем ее таблицей 1. Возьмем каждое из сочетаний таблицы 1 и всеми возможными способами переставим в нем элементы. Получим всего 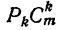размещений, которые и запишем в таблицу 2. Покажем, что в таблице 2 содержатся все размещения из m элементов по k и при этом ни одно размещение не содержится дважды.

Пусть А — произвольное размещение из m элементов по k. Если не обращать внимания на порядок расположения элементов, то А представляет собой некоторое сочетание С из m элементов по k.

Так как в таблице 1 содержатся все сочетания из m элементов no k, в ней содержится и это сочетание С. 3 сочетании С мы переставляли элементы всеми возможными способами. Следовательно, размещение А содержится в таблице 2.

Возьмем теперь два каких-нибудь размещения из таблицы 2. Если они получены из разных сочетаний, то они отличаются друг, от друга элементами. Если они происходят от одного сочетания, они отличаются порядком расположения элементов. В обоих случаях эти размещения различны.

Отсюда вытекает, что

Формула для 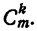может быть преобразована. Умножим числитель и знаменатель на (m — k) Получим

Пример:

В классе 30 учащихся. Сколькими способами можно назначить двух дежурных из них?

Решение:

Искомое число равно числу сочетаний из 30 элементов по 2.

Теорема:

Доказательство:

Эту теорему можно доказать и иначе.

Выбирая какие-нибудь k элементов из данных m, мы составляем некоторое сочетание из m элементов по k. Остальные m — k элементов образуют сочетание из т элементов по m — k.

Таким образом, каждому сочетанию из m элементов по k соответствует одно сочетание из m элементов по m — k и наоборот. Значит число сочетаний из m элементов по k равно числу сочетаний из m элементов по m — k.

Пример:

Некоторые суммы и их свойства

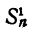
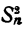
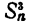
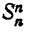
— некоторые числа. Пусть , обозначает сумму всех этих чисел, обозначает сумму всевозможных произведений этих чисел, взятых по два, обозначает сумму всевозможных произведений этих чисел, взятых по три, ит. д, Вообще означает сумму всевозможных произведений этих чисел, взятых по k. Таким образом, обозначает произведение этих чисел

Присоединим к числам (1) еще какое-нибудь число 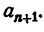. Получим n+1 чисел

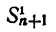
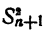
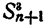
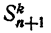
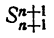
Пусть обозначает сумму всех чисел (2), обозначает сумму всевозможных произведений чисел (2), взятых по два, обозначает сумму всевозможных произведений чисел (2), взятых по три, и т. д. Вообще обозначает сумму всевозможных произведений чисел (2), взятых по k. Таким образом, обозначает произведение чисел (2).

Рассматриваемые суммы обладают следующими свойствами,

Свойство:

Свойство:

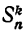
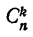
При любом k (1 ≤ k ≤ n) в сумме содержится слагаемых.

Свойство:

Свойства 2 и 3 непосредственно вытекают из способа составления рассматриваемых сумм. Остается доказать справедливость свойства 1.

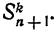
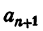
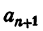
Возьмем какое-нибудь слагаемое, входящее в Такое слагаемое является произведением k чисел, взятых из (2). Возможно одно из двух: либо число в это слагаемое не входит в качестве сомножителя, либо в него сомножителем входит.

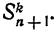
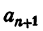
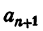
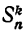
На этом основании разобьем все слагаемые, входящие в , на две группы: к первой группе отнесем те из них, которые не содержат число в качестве сомножителя, ко второй группе отнесем те слагаемые, которые содержат число в качестве сомножителя. Сумма слагаемых первой группы есть , так как эта сумма состоит из всевозможных произведений чисел совокупности (1), взятых по k.

Из суммы, которую составляют слагаемые второй группы, вынесем за скобки 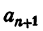. В скобке останется сумма всевозможных произведений чисел совокупности (1), взятых по k — 1.

Следствие:

О произведении двучленов, первые члены которых одинаковы

Рассмотрим произведение n двучленов, имеющих один и тот же первый член:

Источник