Что больше число грэма или бесконечность
10 самых больших и важных чисел
Дети часто задают вопрос: «Какое число самое большое?». Этот вопрос — важный шаг в процессе перехода в мир абстрактных понятий. Ответ, конечно, прост: числа, скорее всего, бесконечны, но есть определенный порог, за которым числа становятся настолько большими, что в них нет смысла, кроме того, что технически они могут существовать. Давайте возьмем десятку гигантских чисел, известных нам, но ограничимся крайне важными понятиями в мире чисел.
Десять в восьмидесятой степени — 1 с 80 нулями — это довольно массивное число, обозначающее примерное число элементарных частиц в известной вселенной, и, говоря элементарные частицы, мы не имеем в виду микроскопические частицы — мы говорим о куда меньших вещах вроде кварков и лептонов — о субатомных частицах. Это число в США и современной Великобритании называют «сто квинквавигинтиллионов». Вроде бы, несложно понять, что это число обозначает количество мельчайших частиц в нашей Вселенной, однако это самое маленькое и простое число в нашем списке.
Один гугол
Слово гугол, несколько измененное, стало часто используемым в современности, благодаря популярной поисковой системе. У этого числа есть интересная история — достаточно просто погуглить. Термин был придуман Милтоном Сироттой в 1938 году, когда ему было 9 лет. И хотя это относительно абстрактное число, и его существование объясняется необходимостью технического существования, ему все-таки нашли применение.
Алексис Лемер поставил мировой рекорд, рассчитав корень тринадцати из стозначного числа. Гугол — это стозначное число, число с сотней нулей. Также предполагается, что от одного до полутора гугол лет с момента Большого Взрыва взорвется самая массивная черная дыра. И тогда Вселенная вступит в так называемую «темную эпоху» — конец той научной вселенной, какой мы ее знаем.
8,5 х 10^185
Длина Планка — это очень маленькая длина, примерно 1,616199 x 10-35, или 0,00000000000000000000000000000616199 метра. В дюймовом кубе этих длин примерно с гугол. Длина и объем Планка играют важную роль в отраслях квантовой физике — например, теории струн — поскольку позволяют производить вычисления на самых мельчайших масштабах. Во вселенной примерно 8,5 x 10^185 объемов Планка. Это достаточно большое число, и ему все же нет практического применения, но оно остается достаточно простым в нашем списке.
2^43,112,609 – 1
Третье по величине число в этом списке — это число всех планковых объемов во Вселенной, и в нем 185 цифр. А в этом числе почти 13 миллионов цифр. Чем это число важно? Это самое большое из известных сегодня простых чисел. Его обнаружили в августе 2008 года в ходе Great Internet Messene Prime Search (GIMPS).
Гуголплекс
Вы наверняка слышали это слово, хотя бы в фильме «Назад в будущее», когда доктор Эммет Браун бормотал «она одна на миллион, одна на миллиард, одна на гуголплекс». Что такое гуголплекс? Помните длину гугола? Единица и сто нулей. А гуголплекс — это десять в степени гугол. Это больше, чем число всех частиц в известной нам части вселенной.
Вы можете отметить, что можно возводить десять в степень гуголплекс и будет еще больше, и так далее, и окажетесь совершенно правы.
Числа Скьюза
Число Скьюза — это верхний предел для математической задачи π(x) > Li(x), хоть и просто выглядящей, но крайне сложной на самом деле. По существу, число Скьюза доказывает, что число x существует и нарушает это правило, если предположить, что гипотеза Римана верна, а число x меньше, чем 10^10^10^36, первое число Скьюза. Даже первое число Скьюза больше гуголплекса. Есть также и самое большое число Скьюза: x меньше, чем 10^10^10^963.
Время возвращения Пуанкаре
Это очень сложная вещь, но основная концепция относительно проста: при наличии достаточного времени, все возможно. Теорема Пуанкаре о возвращении предполагает количество времени, которого было бы достаточно для того, чтобы однажды вся Вселенная вернулась в свое нынешнее состояние, вызванное случайными квантовыми флуктуациями. Короче, «история повторится». Предполагается, что это займет 10^10^10^10^10^1,1 лет.
Число Грэма
В 80-х годах это число попало в Книгу рекордов Гиннесса как самое массивное конечное число, когда-либо использованное в математических доказательствах. Оно было выведено Роном Грэмом как верхний предел для проблем теории Рамси о многоцветных гиперкубах. Число настолько большое, что для его записи используется стрелочная нотация Кнута (метод записи больших чисел) и собственное уравнение Грэма. Метод Кнута и принцип работы стрелок сложно объяснить, но вы можете представить себе это так. 3↑3 превращается в 3^3 или 27, 3↑↑3 превращается в 3^3^3 или 7,625,597,484,987. Вы можете добавить еще одну стрелку к 3↑↑↑3 и выйти на 7,5 триллионов уровней. Само по себе это число значительно больше, чем время возвращения Пуанкаре, поскольку вы можете добавить бесконечное число стрелок, и каждая стрелка будет невероятно увеличивать число.
Число Грэма выглядит так: G=f64(4), где f(n)=3↑^n3. Лучший способ его представить — разложить по полочкам. Первый слой — это 3↑↑↑↑3, что уже невероятно много. Следующий слой — это множество стрелок между тройками. Возьмите эти стрелки и поместите между следующими тройками. Это умножается в 64 раза. Даже сам Грэм не знает первое число, но последние десять вот: 2464195387. Вся наблюдаемая вселенная слишком мала, чтобы вместить в себя обыкновенную десятичную запись числа Грэма.
∞. Бесконечность
Это число известно всем и каждому, оно часто используется для преувеличений — как какой-нибудь «многоллион». Однако это число намного сложнее, чем большинство может представить, и если вы могли представить числа, идущие до этого пункта, именно это число очень странное и противоречивое. Согласно правилам бесконечности, есть бесконечное число нечетных и четных чисел в бесконечности, однако только половина от всех чисел может быть четной. Бесконечность плюс один равна бесконечности, бесконечность минус один равна бесконечности, бесконечность плюс бесконечность равна бесконечности, деленная пополам — тоже бесконечность, бесконечность минус бесконечность — никто не знает, бесконечность, деленная на бесконечность, будет, скорее всего, 1.
Ученые полагают, что в известной вселенной около 10^80 субатомных частиц, но это только известная вселенная. Некоторые предполагают, что вселенная бесконечна. Если это так, то математически достоверно, что есть другая Земля где-то там, где каждый атом складывается таким же образом, как и мы, и наша Земля. Шанс того, что копия Земли существует, невероятно мал, но в бесконечной вселенной это не только может произойти, но и бесконечно много раз.
В бесконечность верят не все. Израильский профессор математики Дорон Зильбергер утверждает, что по его мнению, числа не будут продолжаться вечно, и найдется настолько большое число, что когда вы добавите к нему единицу, вы придете к нулю. И хотя это число едва ли когда будет обнаружено и едва ли кто сможет его вообразить, бесконечность является важной частью математической философии.
Самые большие числа во Вселенной
Гугология — современный термин, однако история изучения самых больших чисел в математике уходит корнями в глубокую древность. Еще Архимед в одном из своих трудов указал, как следует обозначать и записывать гигантские числовые значения — его и называют первым «гугологистом».
Сверхбольшие числа, а вернее, математические объекты, относящиеся к гугологии, называются гугологизмами. Сегодня математики определили их и дали им названия. Это сам гугол — единица со ста нулями, а также гуголплекс, гиггол, гаггол, бугол, число Грэма, траддом, биггол, трултом, тругол и еще — только представьте себе! — несколько тысяч больших чисел.
Наверно, каждый ребенок в детстве задавал родителям вопрос: «Какая самая большая цифра в мире?». Ответ на него будет довольно абстрактный: самые большие числа считаются бесконечными. Они могут быть такими грандиозными, что их практическое применение в реальной жизни и невозможно, и бессмысленно, и единственное, что их оправдывает — сам факт их существования. Однако часть из них может использоваться в космологии — например, для обозначения количества атомов и диаметра видимой части Вселенной, а также в статистической механике.
Гугол
Популярное название поисковой системы выглядит и произносится почти также, как и слово гугол — googol. Число имеет интересную историю: в 2020 году математик Эдвард Казнер гулял по парку с племянниками и обсуждал с ними большие числа. Когда речь зашла о числе со ста нулями, оказалось, что у него нет собственного названия. Тогда один из детей, девятилетний Милтон Сиротта, предложил назвать это число «гугол». Также было предложено название ещё для одного числа: «гуголплекс», численно равного десяти в степени гугол. Так, благодаря этой прогулке, в 1940 году Эдвард Казнер совместно с Джеймсом Ньюманом написал научно-популярную книгу «Новые названия в математике», где и рассказал любителям науки о числах гугол и гуголплекс.
Гугол имеет практическое значение в физике: это обозначение промежутка времени, примерно от 1 до 1.5 гугола лет, которые пройдут со времени Большого взрыва до взрыва самой массивной черной дыры. После этого Вселенная войдет в пятую и последнюю эру своего существования, известную как Эра Темноты, и наступит физический конец ее существования — правда, гипотетический.
Число Грэма
Число Грэма — самая большая цифра в математике. Записать ее проблематично — более того, число невозможно записать даже в форме степеней степеней! Для его записи используется особая формула — нотация Кнута или цепочка Конвея. Число Грэма намного больше гугла и даже гуголплекса (10 в степени гугол). А ведь одного гуглоплекса вполне достаточно, чтобы «вместить» в себя нашу Вселенную. У числа Грэма есть конкретный математический смысл, поэтому оно было занесено в Книгу рекордов Гиннесса как самая большая математическая величина.
10 в 80 степени
Огромное число десять в восьмидесятой степени — это число с 80 нулями после 1. Оно также имеет конкретную область применения, и обозначает примерное количество элементарных частиц во Вселенной. Название числа в современном английском языке — квинквавигинтиллион. Количество элементарных частиц, которые составляют видимую часть Вселенной, может быть невероятно огромным, но это самое маленькое и легкое для понимания число в этом списке.
Как видите, у науки и нашей Вселенной немало загадок, лежащих за гранью человеческого понимания. И большие числа — одни из них. Может быть, их значения когда-то найдет и докажет искусственный интеллект — только времени пройдет не один гугол лет…
Число Грэма и взгляд в бесконечность
Вглядываться в бесконечность можно по-разному. Можно представлять себе всё увеличивающиеся астрономические числа и сопоставлять их с физическими явлениями. Можно всматриваться в выбранную точку фрактала Мандельброта, плавно увеличивая масштаб в 10 198 раз (можно и больше, но в угоду скорости страдает наглядность). Фрактал, сколь малую часть его не бери, остаётся самоподобным и сохраняет дробную структуру.
А можно представлять себе число Грэма так, как его представляет автор статьи «Число Грэма на пальцах». Число Грэма настолько велико, что даже если вы представите себе какое-то чудовищно большое астрономическое число, а потом возведёте его в столь же чудовищную степень, а потом повторите всё это чудовищное число раз — то вы даже не стронетесь с места на шкале того пути, что ведёт к числу Грэма. Чтобы сосчитать до числа Грэма, придётся научиться считать совсем иначе, нежели мы привыкли — представляя, что путь в бесконечность лежит через дописывание нулей к известным нам астрономическим числам. В этой системе счёта загибанию пальца на руке будет соответствовать не прибавление к числу единицы или миллиона, не дописывание нуля или сотен нулей разом, но шаг от сложения к умножению, от умножения к возведению в степень и дальше в невообразимые дали.
Сразу предупреждаю, что все эти упражнения небезыздержечны — не увлекайтесь, берегите своё душевное здоровье. Однако иногда полезно всмотреться в бесконечность, чтобы понять, где ты и что ты ей, как человек, можешь противопоставить.
Для меня в своё время взгляд бесконечность, подобный описанному «на пальцах» числу Грэма, дала функция Аккермана (которую приводят как пример сложной рекурсивной функции в теории алгоритмов). Она тесно связана со стрелочной записью Кнута, используемой в статье про число Грэма.
Если мы возьмём натуральное (т.е. неотрицательное целое) число и применим к нему операцию порядка, равного этому числу, то у нас получится примерно функция Аккермана (на самом деле, она определяется сложнее и от трёх или двух аргументов, но не суть).
Функция Аккермана растёт очень быстро, она растёт невыразимо быстро, она растёт быстрее чего угодно, что вы можете себе представить. Уже на пятом шаге она выходит за границы Вселенной. Но чтобы досчитать до числа Грэма за обозримое число шагов, даже её недостаточно. Нужно взять функцию Аккермана «второго порядка». Т.е. функцию Аккермана от функции Аккермана от функции Аккермана — и так Y раз. Получится эдакая «башенка» функций Аккермана. Вот такая «башенка» высотой в 64 этажа как раз до числа Грэма и досчитает.
Кажется, что осознание невыразимой величины этого числа может раздавить человека. Но не спешите с выводами. Автор упомянутой статьи, пытаясь оценить подступы к этому числу, сравнивает его элементы с числом частиц во Вселенной, сравнивает высоту «башенок» с расстоянием между планетами. Но вся эта кажущаяся с виду невыразимость сводится к числу «полтора». Ладно, пусть «два с половиной».
Поясню. Считать «бесконечность» (в кавычках — ибо любое число всё же конечно) нужно не тем, сколько песчинок она в себе содержит, а тем, сколько раз количество переходит в качество, сколько в ней нетривиальных идей. Посчитаем, сколько нетривиальных идей в числе Грэма. Функция Аккермана с её порядком арифметической операции как аргументом функции — идея раз. Применение функции Аккермана к самой себе — даже на полноценную идею не тянет, так, на половинку (а ведь можно представить и функцию Аккермана третьего порядка, чтобы ещё большее число получить — но тем отчётливее вырожденность идеи). Добавим ещё, собственно, описание задачи, в рамках которой появилось число Грэма (покраска в случайную комбинацию двух цветов диагоналей многомерных гиперкубов), чтобы иметь представление, где остановиться в нашем счёте — и получим две с половиной идеи.
Вроде, с одной стороны, почти необозримая бесконечность — а с другой стороны, тривиальность. Поставьте два зеркала друг напротив друга, встаньте между ними — и вы увидите бесконечное количество всё более тускнеющих отражений. Отражений бесконечное количество, но оригинал у них один — отражаетесь лишь вы сами.
Если в каком-то явлении вы замечаете, что с какого-то момента начинают повторяться лишь ухудшающиеся (в лучшем случае, такие же) копии того, что уже было раньше — то это дурная бесконечность, ложная. Движение по её шкале — лишь видимость жизни, но по сути это западня для вашего сознания.
Или вот был хороший оригинал — и сделали ему сиквел, приквел или ответвление сюжета. Чем наполнить? Известно чем — взять всё то же, что в оригинале, но в бОльших количествах и иначе скомбинированное. Была одна идея, стало полторы. Этих сиквелов можно теперь бесконечное число делать, зарабатывая деньги на тех, кому полюбился оригинал. И опять перед нами дурная бесконечность.
Вообще, возьми любой жанр — и большую часть его составят повторения, ухудшенные копии родоначальника жанра. Если вы чувствуете, что задыхаетесь в засилье этих похожих друг на друга отражений — плывите против течения, ищите источник отражений. Лишь так вы сможете в лабиринте дурной бесконечности отыскать истинный путь.
Неисчислимое: в поисках конечного числа
Древние греки — приверженцы концепций, имеющих строгий логический смысл — всячески избегали концепции бесконечности. Действительно, какое нам дело до бесконечного ряда чисел, если ни записать, ни представить его мы не можем.
В средние века логическую строгость отбросили ради математических результатов и разработали чрезвычайно эффективные алгоритмические методы, оперирующие в вычислениях бесконечностью.
В XX в. стала отчетливо проступать другая проблема. С бесконечностью мы можем разобраться при помощи одного символа (∞), но что делать с числами, которые меньше бесконечности, но при этом невообразимо огромны?
Мы вплотную подошли к числам, едва уступающим «уроборосу», но при этом все еще имеющим теоретическое и практическое значение. Вы, вероятно, могли слышать о числе Грэма, которое является верхней границей для решения определенной проблемы в теории Рамсея. Спустя 88 лет после появления теоремы Рамсея математики готовы отбросить старые методы и пойти еще дальше.
Добро пожаловать в кроличью нору без дна.
Вступление, в котором нужно вспомнить прошлое
В XVII в. математик и философ Блез Паскаль писал о своем страхе перед бесконечностью, о чувстве собственной незначительности при мысли о безбрежных просторах космоса. Интересно, что сказал бы Паскаль о числе Грэма, состоящем из башни чисел высотой от Земли до самой отдаленной звезды, в каждом числе которой прячется своя башня из чисел? Каждый изгиб числа в башне чисел, которая состоит из башни чисел, вмещает в себя башню других чисел — но даже с такой формулировкой мы и близко не подошли к открытию, сделанному Грэмом.
Истоки числа Грэма следует искать в 1928 г., когда молодой математик Фрэнк Рамсей во время работы над статьей о логике заметил удивительную вещь: полная неупорядоченность невозможна. Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высокоупорядоченную структуру.
Догадка, которая была лишь небольшой частью работы о логике, положила начало совершенно новой области математики, называемой теорией Рамсея. Ее часто объясняют на примере вечеринки: предположим, вы хотите найти идеальный баланс между теми, кто знает друг друга, и незнакомцами. Вы рисуете карту отношений всех ваших друзей, связывая двух людей, если они являются друзьями, синей линией, и красной — если они не знакомы друг с другом. Тогда может получиться подобная иллюстрация:
Красота теории Рамсея заключается в том, что задачи в этой области всегда очень легко формулировать. Рассматривая пример с вечеринкой, очень интересно понять, какого количества людей достаточно для образования группы, в которой всегда окажется четверо людей либо знакомых, либо не знакомых друг с другом.
В группе из 17 точек, изображенных на рисунке выше, невозможно найти четыре точки, для которых сеть соединяющих их ребер была бы целиком красной или синей. Поэтому требуется более 17 человек, чтобы среди них обязательно оказалось четверо людей, знакомых или не знакомых друг с другом. На самом деле в группе из 18 человек всегда найдутся либо четверо знакомых, либо четверо не знакомых друг с другом.
Возьмем любое звездное скопление. В нем всегда можно найти группу, которая с очень большой точностью образует какую-нибудь заданную конфигурацию — прямую линию, прямоугольник, ковш.
Математики стараются вычислить, сколь велико должно быть множество звезд, чисел или каких-либо объектов, чтобы можно было гарантировать существование определенной желаемой подструктуры. На решение таких задач часто уходят десятилетия.
Теория Рамсея также имеет большое практическое значение — от организации хорошей вечеринки до построения более совершенных сетей коммуникации и систем передачи и поиска информации. На самом деле очень сложно представить, для каких целей могут послужить многие методы, разработанные для решения задач в теории Рамсея — это самый передовой край математики.
Как и почему Грэм пришел к своему числу
Американский математик Рональд Льюис Грэм (родился в 1935 г.) внес значительный вклад в дискретную математику. Грэм — личность разносторонняя. В свое время он даже был президентом международной ассоциации жонглеров, но прославился исключительно за счет большого положительного целого числа, которое служит верхней границей конкретной проблемы в теории Рамсея.

N-мерный куб всегда содержит 2n вершин. Несмотря на их размерность, n-мерные кубы — это просто графы, вершины которых связаны ребрами
Любой n-мерный куб мы можем превратить в полный граф, просто соединив все вершины. Остальные ребра, сформированные таким образом, находятся внутри или на одной из граней. Представим, что эти края имеют два цвета — красный и синий. Таким образом, Грэм сформулировал интересный вопрос, лежащий в плоскости классической теории Рамсея: при каком минимальном значении N двухцветного k-мерного куба каждая такая раскраска обязательно содержит раскрашенный в один цвет полный подграф с четырьмя вершинами, каждая из которых лежит в одной плоскости?

Полный граф на трехмерном кубе с раскраской ребер в два цвета
В 1971 г. Рональд Грэм и Брюс Ли Ротшильд доказали, что у этой задачи есть решение, и оно представляет собой число, которое больше 6 (нижняя граница), и меньше некоего N. Нижняя граница впоследствии была повышена до 13, а верхняя граница получила название малого числа Грэма. Малое число Грэма меньше числа, попавшего в Книгу рекордов Гиннесса, но это все равно невообразимо огромное число.
В общем-то, задача Грэма не звучит как нечто сверхъестественное — ее может понять и пятиклассник. Но на простые вопросы иногда очень трудно получить ответы. Если решение меньше, чем число Грэма, которое мы знаем, то каков же ответ? Число Грэма, как и некоторые другие большие числа, просто говорит нам, что у некоторой задачи в принципе есть решение, и это решение можно найти. Оптимизировав решение задачи, мы можем сдвинуть число Грэма ближе к 1, и двигать его до тех пор, пока не найдем реального решения.
Как число стало легендой
Итак, Рональд Грэм написал профессиональную математическую работу по теории Рамсея, которая привлекла внимание журналиста Мартина Гарднера. Именно Гарднер ипоспособствовал попаданию числа Грэма в Книгу рекордов Гиннесса, после чего число привлекло внимание широкой общественности.
Проблема, которую Грэм пытался решить, на самом деле была лишь одним конкретным примером применения теории Рамсея. Дальнейшие исследования в этой теории дали математикам бóльшие числа, чем даже число Грэма. Эти числа не являются точным решением проблем, а выступают верхней границей.
Чем же очаровал Грэм людей? Красотой и наглядностью.
Чтобы оперировать гигантскими числами, Грэм использовал быстрорастущие функции. Многие из этих функций знакомы всем — сложение, умножение и возведение в степень. Математики создали новые функции, которые масштабируются намного быстрее.
Для записи числа Грэм использовал стрелочную нотацию Кнута — расширение возведения в степень. Точно так же, как возведение в степень является повторным умножением и обозначается одной стрелкой, направленной вверх, две стрелки вверх обозначают итерационное возведение в степень, три стрелки — повторное итерационное возведение в степень и т.д.
3↑↑5 = 3↑3↑3↑3↑3 = три в степени три в степени 7 625 597 484 987.
Математики поняли, что, имея дело с большими числами, требуется каждый раз использовать новый оператор, который должен быть мощнее предыдущего. ↑↑ — следующий оператором от ↑, так же как ↑ — следующий оператор от умножения, и точно так же, как умножение — это один оператор от сложения. Таким образом, увеличение количества последовательных стрелок увеличивает способность работать с большими числами.
Если добавить еще одну стрелку, то скорость формирования новых чисел значительно возрастет:
3 ↑↑↑ 3 дает нам башню из степеней троек высотой в 7 трлн чисел.
Четыре стрелочки даст число, записать которое будет уже очень трудно. Обратимся к примеру из замечательной статьи «Число Грэма на пальцах»:
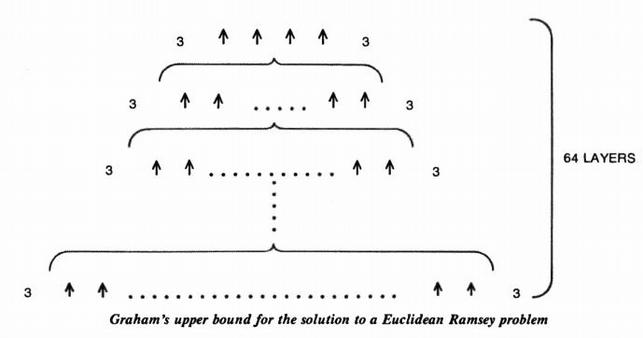
А вот оригинальная иллюстрация, которую Гарднер использовал для объяснения числа Грэма:
Самый верхний уровень равен 3 ↑↑↑↑ 3. Формулу вы видели выше. Под ним находится слой, в котором число стрелочек равно 3 ↑↑↑↑ 3. Далее идет слой, в котором число стрелочек равно числу стрелочек в предыдущем слое. И так до 64-го слоя.
Красота этого выражения в том, что если вы захотите превзойти число Грэма и напишите «супербольшое число = число Грэма + 1», то в математических масштабах ничего не изменится. Все равно что залезть на вершину Эвереста и прыгать на ней — Эверест все равно останется самой высокой горой, на вершину которой вы можете взобраться.
Но где-то в Солнечной системе есть и Олимп, не так ли?
Нотация Бауэрса: начало кроличьей норы
Дальнейшая работа с теорией Рамсея математиков Джозефа Краскала и Харви Фридмана привела к числу TREE(3), у которого даже самая нижняя граница решения является сверхогромной, не говоря о верхней.
Если число Грэма мы хотя бы можем записать, то число TREE(3) невозможно поместить в рамки нотации Кнута. Судите сами:
TREE (3) = … > A A(187196) (4), где даже A 2 (4) больше, чем число атомов во Вселенной, ведь А — функция Аккермана, которая определяется рекурсивно для неотрицательных целых чисел m и n следующим образом:
Используя функцию Аккермана, можно очень легко записать число Грэма ≈ A64(4).
Математики вычислили, что у TREE(3) есть теоретическая граница, которую можно записать с помощью массивной нотации, предложенной в 2002 г. Джонатаном Бауэрсом. В массивной нотации существует пять правил:
Функция возрастает невероятно быстро. Массив из трех элементов <10,100,2>в стрелочной нотации Кнута будет иметь следующий вид: 10 ↑ 2 100.
Тройные массивы Бауэрса полностью идентичны тройным цепочкам обозначения Конвея (еще один метод записи — соединенные горизонтальными стрелками (цепочками) числа, растут быстрее нотации Кнута):
<3,3,3>= 3 → 3 → 3 = 3 ^ (3 ^ (3 ^ (3 ^… 7 625 597 484 987 раз… ^ 3) ^ 3) ^ 3)
Массив из четырех элементов (например <10,100,1,2>) уже больше самого числа Грэма — благодаря хитрости, придуманной Бауэрсом: на четвертом элементе он «оптимизирует» формулу, как раньше мы оптимизировали умножение и возведение в степень, только теперь математик занимается удвоением скобок:
Более подробный разбор этой операции вы можете найти в статье «Bird’s Linear Array Notation».
При этом «самое больше число, использованное в серьезном математическом доказательстве», ограничено между <3,65,1,2>и <3,66,1,2>. Речь сейчас идет только о линейных массивах, а ведь они могут быть и гипермерными. В принципе массив Бауэрса из четырех элементов способен вместить в себя всю нотацию Конвея, а гипермерные массивы (на иллюстрации выше) уже становятся математической гиперигрой.
Красота математики в том, что мы можем работать с данными, которые даже представить невозможно. Любую сложную задачу можно облегчить до невероятно простых значений. Возможно, ответы на некоторые вопросы мы никогда не найдем, но методы, использованные для их решения, могут пригодиться в других областях знаний. Сама проработка этих методов построения иерархий по скорости роста функций совершенствует многие разделы математики.
Бауэрс сделал удачную попытку ответить на вопрос, как с помощью иерархии приемов расширить возможности формальной системы. Фактически мы записываем не само число иносказательным образом, а способ когда-нибудь прийти к этому числу хотя бы в теории.
Нотации Бауэрса стали отличной возможностью подобраться к пониманию функции TREE. Конечно, определить величину TREE(3) мы не можем, но с помощью итерационного «улучшения» нотации, проведенного английским математиком Крисом Бердом, удалось выяснить, что TREE(3) > <3,6,3[1[1¬1,2]2]2>.
TREE(3)
TREE — быстрорастущая функция в теории графов, разработанная математиком Харви Фридманом.
Предположим, что мы имеем последовательность k-пронумерованных деревьев T1, T2,… со следующими свойствами:
BIG FOOT является аналогом числа Райо — его определение почти идентично. BIG FOOT расширяет теорию множеств первого порядка, используя уникальную область дискурса, называемую oodleverse, с использованием языка, называемого first-orderoodletheory (FOOT), и обобщая теорию множеств n-го порядка сколь угодно большого n.
Пусть FOOT(n) обозначает наибольшее натуральное число, однозначно определяемое в языке FOOT не более чем в n символах. BIG FOOT определяется как FOOT 10 (10 100 ), где FOOT a (n) — это FOOT(n) (рекурсия).
BIG FOOT таким образом равен
Поиски конечного числа продолжаются. Будет ли оно когда-нибудь найдено?
Блез Паскаль так описал экзистенциальный ужас, охватывающий его при мысли о безграничности мира: «Вечная тишина этого бесконечного пространства пугает меня». Числа дают нам возможность установить рамки понимания и границы дозволенного, взять под контроль страх уробороса. Они — наше реликтовое излучение, возможность подойти к метафорическому краю мира. Но, как в космосе нельзя долететь до такого места, где будет висеть табличка «конец Вселенной», так и в математике невозможно достичь последнего рубежа. Впрочем, это нам еще предстоит проверить.