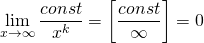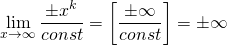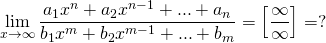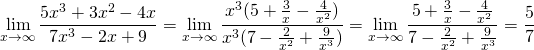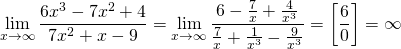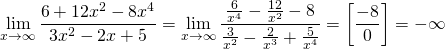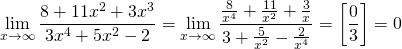Что будет если бесконечность делить на бесконечность
Что будет если бесконечность делить на бесконечность
http://uzdikbalabaksha.kz/index.php/competitions/9-zdik-sport-jirmesi
Здравствуйте! Проголосуйте пожалуйста за детский садик Акбота в городе Акколь! Спасибо огромное .
Так как это полные абстракции («бесконечно большие величины»), то с ними можно производить стандартные математические действия.
Понял
,В МАРТЕ МОЖЕТ СМОГУ НОВЫЙ КУПИТЬ.
Интересно вы рассуждаете. Ну допустим, что профессора не люди, которые никогда не смеются и полностью потеряны. Поэтому вот такой у меня вопрос: А что значит потеряно (или не потеряно) и для кого?
не уверен, что я прав, но по моему любое действия связанное с бесконечностью порождает бесконечность.
Не, бесконечности бывают разные)
Величины могут стремиться к бесконечности с экспоненциальной скоростью, могут с линейной, полиномиальнй и тд. Если взять отношение 2х экспоненциальных величин, или двух линейных и устремить их к бесконечности, то в первом случае может получиться или бесконечнось или константа, а во втором только константа.
но, подождите, здесь берутся величины, которые стремятся к бесконечности, с разной скоростью, или с разной прогрессии в скорости, стремящиеся к бесконечности. Величины ведь только стремятся, но сами не являются бесконечностью. Хотя они могут породить бесконечность, как достигшая величина n в n бесконечной степени.
В пределе они стремятся к бесконечности.
Можно. Но это неопределенность. Дохрена разделить на дофига не имеет отпределенного решения )
Делить возможно нет, а вот прибавлять. Галактики неосязаемы, но их много во вселенной.
тебе оно надо? Тут судьбы людей решаются, а ты со своими бесконечностями)))
Основные неопределенности пределов и их раскрытие
В предыдущей статье мы рассказывали, как правильно вычислять пределы элементарных функций. Если же мы возьмем более сложные функции, то у нас в расчетах появятся выражения с неопределенным значением. Они и называются неопределенностями.
Выделяют следующие основные виды неопределенностей:
Мы перечислили все основные неопределенности. Другие выражения в различных условиях могут принимать конечные или бесконечные значения, следовательно, они не могут считаться неопределенностями.
Раскрытие неопределенностей
Раскрыть неопределенность можно:
С помощью замечательных пределов;
С помощью правила Лопиталя;
Заменив одно бесконечно малое выражение на эквивалентное ему выражение (как правило, это действие выполняется с помощью таблицы бесконечно малых выражений).
Всю информацию, представленную выше, можно наглядно представить в виде таблицы. С левой стороны в ней приводится вид неопределенности, с правой – подходящий метод ее раскрытия (нахождения предела). Этой таблицей очень удобно пользоваться при расчетах, связанных с нахождением пределов.
| Неопределенность | Метод раскрытия неопределенности |
| 1. Деление 0 на 0 | Преобразование и последующее упрощение выражения. Если выражение имеет вид sin ( k x ) k x или k x sin ( k x ) то нужно использовать первый замечательный предел. Если такое решение не подходит, пользуемся правилом Лопиталя или таблицей эквивалентных бесконечно малых выражений |
| 2. Деление бесконечности на бесконечность | Преобразование и упрощение выражения либо использование правила Лопиталя |
| 3. Умножение нуля на бесконечность или нахождение разности между двумя бесконечностями | Преобразование в » open=» 0 0 или » open=» ∞ ∞ с последующим применением правила Лопиталя |
| 4. Единица в степени бесконечности | Использование второго замечательного предела |
| 5. Возведение нуля или бесконечности в нулевую степень | Логарифмирование выражения с применением равенства lim x → x 0 ln ( f ( x ) ) = ln lim x → x 0 f ( x ) |
Разберем пару задач. Эти примеры довольно простые: в них ответ получается сразу после подстановки значений и неопределенности при этом не возникает.
Решение
Выполняем подстановку значений и получаем ответ.
Решение
Значит, мы можем преобразовать предел в следующее выражение:
Далее мы приведем примеры решений задач на раскрытие неопределенностей с использованием метода преобразования. На практике выполнять это приходится довольно часто.
Решение
Выполняем подстановку значений.
В итоге у нас получилась неопределенность. Используем таблицу выше, чтобы выбрать метод решения. Там указано, что нужно выполнить упрощение выражения.
Как мы видим, упрощение привело к раскрытию неопределенности.
Решение
Подставляем значение и получаем запись следующего вида.
Домножение знаменателя выполняется для того, чтобы потом можно было воспользоваться формулой сокращенного умножения (разность квадратов) и выполнить сокращение.
Как мы видим, в результате этих действий нам удалось избавиться от неопределенности.
Важно отметить, что при решении подобных задач подход с использованием домножения используется очень часто, так что советуем запомнить, как именно это делается.
Решение
Выполняем разложение числителя на множители:
Теперь делаем то же самое со знаменателем:
Мы получили предел следующего вида:
Как мы видим, в ходе преобразования нам удалось избавиться от неопределенности.
Решение
Решение
lim x → ∞ x 8 + 11 3 x 2 + x + 1 = » open=» ∞ ∞
lim x → ∞ x 8 + 11 3 x 2 + x + 1 = » open=» ∞ ∞ = lim x → ∞ x 8 + 11 3 x 8 3 x 2 + x + 1 x 8 3 = = lim x → ∞ 1 + 11 x 8 3 1 x 2 3 + 1 x 5 3 + 1 x 8 3 = 1 + 11 ∞ 3 1 ∞ + 1 ∞ + 1 ∞ = 1 + 0 3 0 + 0 + 0 = 1 0 = ∞
Решение
Выводы
В случае с пределом отношений возможны три основных варианта:
Если степень числителя равна степени знаменателя, то предел будет равен отношению коэффициентов при старших степенях.
Если степень числителя будет больше степени знаменателя, то предел будет равен бесконечности.
Если степень числителя меньше степени знаменателя, то предел будет равен нулю.
Другие методы раскрытия неопределенностей мы разберем в отдельных статьях.
Пределы на бесконечность на бесконечность. Примеры.
Рассмотрим пределы на раскрытие неопределенности вида бесконечность на бесконечность.
Сначала учтем следующее:
— если при вычислении предела в числителе дроби стоит число, то
— это предел на неопределенность вида бесконечность, деленная на бесконечность (или просто бесконечность на бесконечность).
Чтобы найти предел, надо раскрыть неопределенность вида бесконечность на бесконечность. Для этого и в числителе, и в знаменателе выносим за скобки степень с наибольшим показателем. Затем сокращаем на нее.
В дальнейшем просто делим почленно числитель и знаменатель (то есть каждое слагаемое) на старшую степень икса.
2)
А теперь сделаем выводы. Пределы на неопределенность бесконечность на бесконечность сводятся к одному из трех вариантов:
Что будет если бесконечность делить на бесконечность
Во всем мире школьников учат, что делить на ноль нельзя. Корень проблемы — в бесконечности. Деление на ноль вызывает бесконечность примерно так же, как доска для спиритических сеансов — духов из другого мира. Это рискованно. Не ходите туда. Философско-математические подробности вышеизложенного — в этой статье, подготовленной по книге «Бесконечная сила».
Бесконечность
Когда-то в далекие доисторические времена кто-то понял, что числа никогда не заканчиваются. Вместе с этой мыслью родилась бесконечность. Это числовой аналог глубин, скрытых в нашей психике, в наших ночных кошмарах о бездонных ямах и в наших надеждах на вечную жизнь.
Насколько велика Вселенная? Сколько длится вечность? Насколько могуществен Бог? Тысячи лет бесконечность сбивает с толку лучшие умы человечества во всех областях мысли — от религии и философии до науки и математики. Ее запрещали, объявляли вне закона и отвергали. Во времена инквизиции монах Джордано Бруно был сожжен заживо на костре за предположение, что Бог в своей бесконечной силе создал бесчисленные миры.
Деление на ноль
Тем, кто не в силах сопротивляться искушению и желает понять, почему в тенях скрывается бесконечность, советуем поделить 6 на какое-нибудь маленькое число, близкое к нулю, но не равное ему, например 0,1. В этом ничего запретного нет. Если разделить 6 на 0,1, получится 60, довольно прилично.
Поделим 6 на еще меньшее число, скажем 0,01; ответ будет больше — 600. Если мы отважимся разделить 6 на число, которое гораздо ближе к 0, допустим, на 0,0000001, то ответ будет еще больше и составит 60 000 000.
Тенденция ясна. Чем меньше знаменатель, тем больше частное. В пределе, когда знаменатель приближается к нулю, частное стремится к бесконечности.
Вот настоящая причина, почему нельзя делить на 0.
Малодушные говорят, что ответ неопределенный. Но на самом деле он бесконечный.
Делить на ноль — это норма. Часть 1
Говорят, можно поделить на ноль если определить результат деления на ноль. Просто нужно расширить алгебру. По странному стечению обстоятельств найти хоть какой-то, а лучше понятный и простой, пример такого расширения не удается. Чтобы исправить интернет нужна либо демонстрация одного из способов такого расширения, либо описание почему это не возможно.
Disclaimer
Цель данной статьи — объяснить «человеческим языком», как работают фундаментальные основы математики, структурировать знания и восстановить упущенные причинно-следственные связи между разделами математики. Все рассуждения являются философскими, в части суждений расходятся с общепринятыми (следовательно, не претендует на математическую строгость). Статья рассчитана на уровень читателя «сдал вышку много лет назад».
Понимание принципов арифметики, элементарной, общей и линейной алгебры, математического и нестандартного анализа, теории множеств, общей топологии, проективной и аффинной геометрии — желательно, но не обязательно.
В ходе экспериментов ни одна бесконечность не пострадала.
Пролог
Выход «за рамки» — это естественный процесс поиска новых знаний. Но не всякий поиск приносит новое знание и следовательно пользу.
1. Вобще-то уже все поделили до нас!
1.1 Аффинное расширение числовой прямой
Слева и справа от нуля функция уходит в разные стороны «небытия». В самом нуле вообще “омут” и ничего не видно.
Вместо того, чтобы бросаться в «омут» с головой, посмотрим что туда втекает и что оттуда вытекает. Для этого воспользуемся пределом — основным инструментом математического анализа. Основная “фишка” в том, что предел позволяет идти к заданной точке так близко, как это возможно, но не “наступить на нее”. Такая себе “оградка” перед “омутом”.

Оригинал
Хорошо, «оградку» поставили. Уже не так страшно. У нас есть два пути к «омуту». Зайдем слева — крутой спуск, справа — крутой подъем. Сколько к “оградке” не иди, ближе она не становится. Пересечь нижнее и верхнее «небытие» никак не выходит. Возникают подозрения, может мы идем по кругу? Хотя нет, числа-то меняются, значит не по кругу. Пороемся в сундучке с инструментами математического анализа еще. Кроме пределов с «оградкой» в комплекте идет положительная и отрицательная бесконечности. Величины совершенно абстрактные (не являются числами), хорошо формализованы и готовы к употреблению! Это нам подходит. Дополним наше «бытие» (множество вещественных чисел) двумя бесконечностями со знаком.
Именно это расширение позволяет брать предел при аргументе стремящемся к бесконечности и получить бесконечность в качестве результата взятия предела.
Есть два раздела математики которые описывают одно и тоже используя разную терминологию.
С геометрической точки зрения выполнено аффинное расширение числовой прямой. То есть привычная последовательность вещественных чисел “сжата” так, чтобы можно было оперировать границами этой последовательности. В качестве границ (условных) введены две абстрактные бесконечно большие величины. Расширение аффинное, но это не значит что оно пришло из Греции, это значит что сохраняется относительное положение точек (в нашем случае чисел) на прямой. Отсюда и следует, что сохраняются отношения “больше” и ”меньше” как для чисел между собой, так и в сравнении с границами.
С точки зрения общей топологии выполнена двухточечная компактификация числовой прямой путем добавления двух идеализированных точек (бесконечностей с противоположным знаком).
1.2 Проективное расширение числовой прямой
Прогуливаясь по графику 
Попробуем состыковать обе границы «бытия» так, как это делали наши предки. Перейдем на одно измерение выше. Отобразим одномерную линию на двумерной плоскости.
После стыковки наличие двух знаковых бесконечностей теряет смысл. Вместо них можно ввести одну общую точку пересечения, беззнаковую бесконечность.
Эта стыковка очень похожа на линию перемены даты находящуюся (в основном), между часовыми поясами UTC+12 и UTC-12 в Тихом океане. Именно там находится телепорт из сегодня во вчера и из сегодня в завтра. У нас же телепорт из сверхмалых в сверхбольшие.
По факту это самостоятельное расширение, проведенное над исходным множеством вещественных чисел. Данное расширение не основывается на рассмотренном ранее аффинном расширении.
С геометрической точки зрения выполнено проективное расширение числовой прямой (есть информация на wolfram.com). То есть введена идеализированная точка которая соединяет оба конца вещественной прямой. Так как расширение не аффинное, сравнение вещественных чисел с бесконечностью не определено.
С точки зрения общей топологии выполнена одноточечная компактификация числовой прямой путем добавления идеализированной точки (бесконечности без знака).
Аналогичным расширением над полем комплексных чисел является широко известная в математических кругах Сфера Римана.
Хорошо, избавились от знака минус. Однако в нуле у нас разрыв второго рода и устранимой точкой разрыва его нельзя считать по определению. Нарушается требование «конечности» предела. Соответственно мы не можем судить о равенстве предела справа и слева.
Но так как приближение к бесконечности выполняется по одинаковым правилам, мы можем утверждать что пределы слева и справа совпадают. Соответственно мы можем принять наш разрыв за точку устранимого разрыва в бесконечности.
Посмотрим внимательнее, как мы оперируем бесконечно большими и малыми величинами. При операциях мы часто пренебрегаем малыми низшего порядка попросту отбрасывая их при записи результата.
Аналогичная ситуация при нахождении производных
Отбрасывая «мелочевку» мы теряем информацию! Это хорошо видно на примере взятия пределов. Рассмотрим две функции, которые стремятся к положительной бесконечности при стремлении аргумента к нулю справа.
Однако одинаковая запись результата взятия предела не свидетельствует о их равенстве. Данные бесконечности разного порядка и это подтверждается отсутствием конечного предела в отношении одной функции к другой.
В нестандартном анализе такие упрощения не допустимы. Поле вещественных чисел расширяется путем введения гиперреальных чисел. Бесконечно малые представлены в виде привычного значения — ноль, но в довесок хранится вся выкинутая “мелочевка”. Для бесконечно больших потенциальная бесконечность (две или одна — неважно), разбивается на множество актуальных бесконечностей. С одной стороны мы усложняем (теряем возможность поглощения/пренебрежения). С другой стороны мы приобретаем возможность сравнения бесконечно малых и бесконечно больших величин. А это значит что мы можем рассматривать бесконечности как числа.
Для дальнейших рассуждений понятие актуальной бесконечности нам больше не потребуется. Мы возвращаемся в привычный мир где будем оперировать понятием бесконечность, подразумевая потенциальную бесконечность.
Хорошо, пределы совпадают. Теперь, похоже, все готово для устранения разрыва между ними.
В математической модели, использующей проективное расширение числовой прямой, деление на ноль определено.
Создается впечатление что наша задача решена. Однако не будем спешить, посмотрим к каким последствиям это привело. В дополнение к делению в системе определены следующие операции (напомним, что бесконечность беззнаковая).
Как следствие, часть тождеств перестает вести себя так как мы привыкли. Однако, они не исчезли бесследно. Дистрибутивный закон работает только справа налево (т.е. в случае, когда правая часть равенства определена). Это один из ярких примеров негативных последствий. Другие же тождества сохранилась в более-менее устойчивой форме.
1.2 Колесо
На введении беззнаковой бесконечности все не остановилось. Для того чтобы выбраться из неопределенностей нужно второе дыхание.
Итак, у нас есть множество вещественных чисел и две неопределенности 1/0 и 0/0. Для устранения первой мы выполнили проективное расширение числовой прямой (то есть ввели беззнаковую бесконечность). Попробуем разобраться со второй неопределенностью вида 0/0. Сделаем аналогично. Дополним множество чисел новым элементом, представляющим вторую неопределенность.
Определение операции деления основано на умножении. Это нам не подходит. Отвяжем операции друг от друга, но сохраним привычное поведение для вещественных чисел. Определим унарную операцию деления, обозначаемую знаком «/».
С точки зрения общей алгебры мы оперировали полем. А в поле, как известно, определены всего две операции (сложение и умножение). Понятие деления выводится через обратные, а если еще глубже, то единичные элементы. Внесенные изменения превращают нашу алгебраическую систему в моноид как по операции сложения (с нулем в качестве нейтрального элемента), так и по операции умножения (с единицей в качестве нейтрального элемента).
В трудах первооткрывателей не всегда используются символы ∞ и ⊥. Вместо этого можно встретить запись в виде /0 и 0/0.
Мир уже не так прекрасен, не правда ли? Все же не стоит спешить. Проверим, справятся ли новые тождества дистрибутивного закона с нашим расширенным множеством 
На этот раз результат намного лучше.
Стоит отметить, существуют и другие алгебраические системы с делением. Например, «луга» (common meadows). Они чуть проще, так как не расширяют пространство, вводя новые элементы. Цель достигается как в колесах, трансформацией операций сложения и умножения, а так же отказом от бинарного деления.
Возможность «передвигать неизвестные» для математики норма. Но все эти обертки не дают ответа на главный вопрос, что же там внутри?