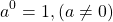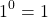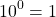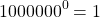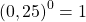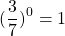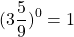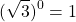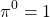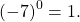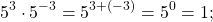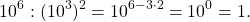Что будет если возвести в нулевую степень
Степень 0
В алгебре возведение с нулевую степень встречается часто. Что такое степень 0? Какие числа можно возводить в нулевую степень, а какие — нет?
Любое число в нулевой степени, за исключением нуля, равно единице:
Таким образом, какое бы число ни возвели в степень 0, результат всегда получится одинаковый — единица.
И 1 в степени 0, и 2 в степени 0, и любое другое число — целое, дробное, положительное, отрицательное, рациональное, иррациональное — при возведении в нулевую степень дает единицу.
Единственное исключение — нуль.
Нуль в нулевой степени не определен, такое выражение не имеет смысла.
То есть в нулевую степень можно возводить любое число, кроме нуля.
Если при упрощении выражения со степенями получается число в нулевой степени, его можно заменить единицей:
Если при упрощении получается переменная или выражение с переменными в нулевой степени, пишем дополнительное условие — основание степени должно быть отличным от нуля:
Число в нулевой степени
Возведение в степень является одним из основных математических действий, без которых невозможны сложные расчеты. При этом отдельного рассмотрения заслуживает нулевая степень числа.
Возведение числа в нулевую степень
Известно, что при x 0 любое x равно 1 (x 0 = 1). Чтобы доказать это, нужно выяснить, откуда собственно взялся этот ноль?
Для этого вспомним формулы сложения и вычитания степеней.
7 3 = 7 2+1 = 7 2 × 7 1 = 7 × 7 × 7, ⇒
7 0 = 7 3-3 = 7 3 ÷ 7 3 = 1
Доказательство получено. Однако есть исключение из этого правила.
Парадокс нуля
Здесь все гораздо сложнее, но не настолько, чтобы не разобраться.
Известно, что 0 x = 0. Например: 0 4 = 0 × 0 × 0 × 0 = 0
Почему же мы часто встречаем выражение 0 0 = 1?
Подберем значения по табл.1.
Таблица 1. Функция ƒ(x) = x x
| x | x x |
| 1 | 1 |
| 0,9 | 0,909 |
| 0,8 | 0,836 |
| 0,7 | 0,779 |
| 0,6 | 0,736 |
| 0,5 | 0,707 |
| 0,4 | 0,693 |
| 0,3 | 0,697 |
| 0,2 | 0,725 |
| 0,1 | 0,794 |
| 0,01 | 0,955 |
| 0,001 | 0,993 |
Как видим, с определенного момента значение x x растет вместе с уменьшением x. В этом нет ничего сверхъестественного, это всего лишь пример действия формулы
Изобразим это на графике

Таким образом, делаем предположение, что это выражение является пределом.
Выразить это можно так:
Проверим, вычислив это значение.
Преобразуем основание выражения. Получаем:
x x = (e ln x ) x = e x ln x
Получаем следующее выражение:
Пользуемся правилом Лопиталя:
Официальная позиция современной математики гласит, что выражение 0 0 — представляет собой неопределенность, то есть не имеет точного значения.
Однако на практике, при расчетах, его значение подстраивается под конкретные требования. И чаще всего в этих случаях оно равно единице. Чтобы лучше разобраться с темой нулевой степени, советуем посмотреть видео ниже.
Числа. Степень числа.
То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5 6 и говорят «пять в шестой степени».
Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.
В общем виде степень с основанием «a» и показателем «n» записывается так
Возвести число a в степень n – значит найти произведение n множителей, каждый из которых равен а
Если основание степени «а» равно 1, то значение степени при любом натуральном n будет равно 1. Например, 1 5 =1, 1 256 =1
Если возвести число «а» возвести в первую степень, то получим само число a: a 1 = a
Особыми считают вторую и третью степень числа. Для них придумали названия: вторую степень называют квадратом числа, третью – кубом этого числа.
-при нахождении степени положительного числа получается положительное число.
-при вычислениях нуля в натуральной степени получаем ноль.
— при вычислении степени отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.
Если решить несколько примеров на вычисление степени отрицательных чисел, то получится, что если мы вычисляем нечётную степень отрицательного числа, то в результате будет число со знаком минус. Так как при умножении нечётного количество отрицательных сомножителей получаем отрицательное значение.
Если же мы рассчитываем четную степень для отрицательного числа, то в результате будет положительное число. Так как при умножении чётного количества отрицательных сомножителей получаем положительное значение.
Свойства степени с натуральным показателем.
Чтобы умножить степени с одинаковыми основаниями мы основания не меняем, а показатели степеней складываем:
Чтобы разделить степени с одинаковыми основаниями основание не меняем, а показатели степеней вычитаем:
При расчетах возведения степени в степень основание не меняем, а показатели степеней умножаем друг на друга.
например: (2 3 ) 2 = 2 3·2 = 2 6
Если необходимо рассчитать возведение в степень произведения, то в эту степень возводится каждый множитель
При выполнении расчетов по возведению в степень дроби мы в данную степень возводим числитель и знаменатель дроби
Последовательность выполнения расчетов при работе с выражениями содержащими степень.
При выполнении расчетов выражений без скобок, но содержащих степени, в первую очередь производят возведение в степень, потом действия умножение и деление, и лишь потом операции сложения и вычитания.
Если необходимо вычислить выражение содержащие скобки, то сначала в указанном выше порядке делаем вычисления в скобках, а потом оставшиеся действия в том же порядке слева направо.
Очень широко в практических вычислениях для упрощения расчетов используют готовые таблицы степеней.
Что будет если возвести в нулевую степень
Ответы:
если учесть, что a^x=e^x*ln(a), то получается, что таки 0^0=1 (предел, при х->0)
хотя и ответ «неопределенность» тоже приемлем
Ноль в математике это не пустота, это число очень близкое к «ничему», точно также как и бесконечность только на оборот
Распишите:
0^0 = 0^(a-a) = 0^a * 0^(-a) = 0^a / 0^a = 0 / 0
Получается в этом случае мы делим на ноль, а эта операция над полем вещественных чисел не определена.
Для ответа необходимо авторизироваться
Похожие вопросы:
RPI.su — самая большая русскоязычная база вопросов и ответов. Наш проект был реализован как продолжение популярного сервиса otvety.google.ru, который был закрыт и удален 30 апреля 2015 года. Мы решили воскресить полезный сервис Ответы Гугл, чтобы любой человек смог публично узнать ответ на свой вопрос у интернет сообщества.
Все вопросы, добавленные на сайт ответов Google, мы скопировали и сохранили здесь. Имена старых пользователей также отображены в том виде, в котором они существовали ранее. Только нужно заново пройти регистрацию, чтобы иметь возможность задавать вопросы, или отвечать другим.
Чтобы связаться с нами по любому вопросу О САЙТЕ (реклама, сотрудничество, отзыв о сервисе), пишите на почту admin@rpi.su. Только все общие вопросы размещайте на сайте, на них ответ по почте не предоставляется.
Чему будет равняться ноль, если его возвести в нулевую степень?
Из свойств степеней: a^n / a^m = a^(n-m) если n=m, результат будет единица кроме естественно a=0, в этом случае (поскольку ноль в любой степени будет нулём) имело бы место деление на ноль, поэтому 0^0 не существует
Счёт на разных языках
Названия числительных от 0 до 9 на популярных языках мира.
| Язык | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Английский | zero | one | two | three | four | five | six | seven | eight | nine |
| Болгарский | нула | едно | две | три | четири | пет | шест | седем | осем | девет |
| Венгерский | nulla | egy | kettõ | három | négy | öt | hat | hét | nyolc | kilenc |
| Голландский | nul | een | twee | drie | vier | vijf | zes | zeven | acht | negen |
| Датский | nul | en | to | tre | fire | fem | seks | syv | otte | ni |
| Испанский | cero | uno | dos | tres | cuatro | cinco | seis | siete | ocho | nueve |
| Итальянский | zero | uno | due | tre | quattro | cinque | sei | sette | otto | nove |
| Литовский | nulis | vienas | du | trys | keturi | penki | ðeði | septyni | aðtuoni | devyni |
| Немецкий | null | ein | zwei | drei | vier | fünf | sechs | sieben | acht | neun |
| Русский | ноль | один | два | три | четыре | пять | шесть | семь | восемь | девять |
| Польский | zero | jeden | dwa | trzy | cztery | piêæ | sze¶æ | siedem | osiem | dziewiêæ |
| Португальский | um | dois | três | quatro | cinco | seis | sete | oito | nove | |
| Французский | zéro | un | deux | trois | quatre | cinq | six | sept | huit | neuf |
| Чешский | nula | jedna | dva | tøi | ètyøi | pìt | ¹est | sedm | osm | devìt |
| Шведский | noll | ett | tva | tre | fyra | fem | sex | sju | atta | nio |
| Эстонский | null | üks | kaks | kolm | neli | viis | kuus | seitse | kaheksa | üheksa |
Отрицательная и нулевая степень числа
Нулевая, отрицательная и дробная степень
Нулевой показатель
Возвести данное число в некоторую степень значит повторить его сомножителем столько раз, сколько единиц в показателе степени.
Согласно этому определению, выражение: a 0 не имеет смысла. Но чтобы правило деления степеней одного и того же числа имело значение и в том случае, когда показатель делителя равен показателю делимого, введено определение:
Нулевая степень любого числа будет равна единице.
Отрицательный показатель
Пример 1. Если данное число состоит из 5 сотен, 7 десятков, 2 единиц и 9 сотых долей, то его можно изобразить так:
Пример 2. Если данное число состоит из a десятков, b единиц, c десятых и d тысячных долей, то его можно изобразить так:
Действия над степенями с отрицательными показателями
При умножении степеней одного и того же числа показатели складываются.
При делении степеней одного и того же числа из показателя делимого вычитается показатель делителя.
Чтобы возвести в степень произведение, достаточно возвести в эту степень каждый сомножитель отдельно:
Чтобы возвести в степень дробь, достаточно возвести в эту степень отдельно оба члена дроби:
При возведении степени в другую степень показатели степеней перемножаются.
Дробный показатель
Если k не есть число кратное n, то выражение: 
Благодаря введению нового символа, извлечение корня всегда может быть заменено возведением в степень.
Действия над степенями с дробными показателями
Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для целых показателей.
При доказательстве этого положения, будем сначала предполагать, что члены дробей: 

В частном случае n или q могут равняться единице.
При умножении степеней одного и того же числа дробные показатели складываются:
При делении степеней одного и того же числа с дробными показателями из показателя делимого вычитается показатель делителя:
Чтобы возвести степень в другую степень в случае дробных показателей, достаточно перемножить показатели степеней:
Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:
Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.
Почему число в степени 0 равно 1?
Можно ли 0 возводить в квадрат
Содержание статьи
Можно ли ноль возводить в квадрат?
Интересный вопрос: можно ли ноль возводить в квадрат? Что получится, если выполнить это, казалось бы, простое действие? Ведь целое число, возведенное в квадрат должно увеличиться, если это не единица.
Теоретически, ноль можно возводить в любую степень. Ведь при умножении любого числа на ноль, получается ноль. А возведение в квадрат – это умножение числа на само себя.
Но в математике ноль возводить в степень не принято, так как это действие не имеет никакого смысла. В нулевую степень можно возводить числа, а вот сам ноль в степени не возводится. Бывает, что при выполнении упрощения выражения со степенями получается, что ноль остается в какой-то степени.
В школьной программе такие примеры если и встречаются, то очень редко. Исключительно для того, чтобы проверить знания учеников и их смекалку. Ведь если на экзамене попадется такой пример, где ноль будет возведен в квадрат, ученик можно вспомнить про правило с возведением числа в нулевую степень, и написать, что получится единица.
Не существует такого числа, которое при умножении на ноль даст отличный от нуля результат.
Ноль в квадрате, как и в любой другой степени, всегда будет равен нулю.
Нулевая степень числа
А вот любое число, возведенное в нулевую степень, будет равно единице. И это тоже нужно знать, как и то простое правильно, что нельзя делить на ноль.