для определения высоты дерева можно использовать зеркало так как показано на рисунке 203
Для определения высоты дерева можно использовать зеркало
Что ты хочешь узнать?
Ответ
тр.EFD (по двум углам) и
отсюда EF=153*4=612см.
Ответ: 612см.
Подробное решение номер 581 по геометрии для учащихся 7 класса, авторов Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдин 2016
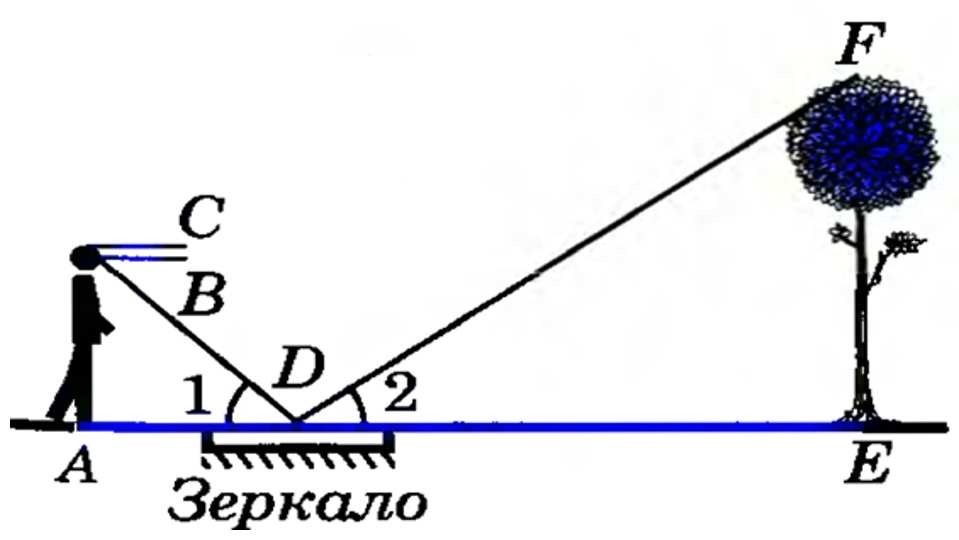
581 Для определения высоты дерева можно использовать зеркало так, как показано на рисунке 203. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека (точку В). Определите высоту дерева, если АС =165 см, ВС =12 см, AD = 120 см, DE = 4,8 м, ∠l = Z2.
решите пожалуйста! для определения высоты дерева можно использовать зеркало так, как показано на данном ниже рисунке. луч СЕ, отражаясь от зеркала в точке Е, попадает в глаз человека — точку А. определите высоту дерева, если АВ=160 см, ВЕ=240 см, ДЕ= 9 м
Лучший ответ:
Углу AEB= углу CED = a т.к. отражается от зеркала
CD-? высота дерева
tg(a)=AB/BE; tg(a) =CD/ED, отсюда AB/BE=CD/ED
выразим в метрах
АВ =160 см = 1.6 м
ВЕ =240 см = 2.4 м
CD=ED*(AB/BE)= 9*(1.6/2.4)=6 м высота дерева
Другие вопросы:
Аллотропию имеет S, N, C, P
Решите уравнение (/-это дробь) 3.557 Х/2 =4
Выпишите номера идиоадаптации 1)возникновение теплокровности у птиц2)отсутствие хлорофила у повилики3)образование у насекомых крыльев разной формы4)разная окраска цветов у покрыосеменных растений5)отсутствие крыльев у тлей6)появление спорового размножения7)появление легочного дыхания8)формирование иголок у кактусов9)плохо развитые глаза у крота10)образование плоской формы тела у камбалы11)появление хитинового покрова у членистоногих 12)формирование длинного языка у хамелеона 13)отсутствие органов чувств у бычьего цепня14)исчезновение пищиварительной системы у ленточных червей 15)внутренне оплодотворение у пресмыкающихся
Презентация «Подобные треугольники. Решение практических задач»
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
«Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение». В. Произволов
ТЕМА УРОКА: Подобие треугольников. Решение практических задач.
Верно ли утверждение? Два треугольника подобны, если их углы соответственно равны и сходственные стороны пропорциональны. ДА Два равносторонних треугольника всегда подобны. ДА
ДА Верно ли утверждение? Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
ЗАДАЧА №2 Подобны ли треугольники, изображенные на рисунке? Вычислите A. Подобны по II признаку. A = 61 º
K ЗАДАЧА №3 Докажите, что ΔDLK ̴ ΔQRS. Подобны по III признаку. ( ))
В книге Жюля Верна повествуется о событиях, происходящих на вымышленном острове, где остановился капитан Немо на своей подводной лодке «Наутилус». Основными персонажами являются пятеро американцев, которые оказываются на необитаемом острове в Южном полушарии. «ТАИНСТВЕННЫЙ ОСТРОВ»
500 15 Шест = 12футов (воткнул в песок на 2 фута) ИЗМЕРЕНИЕ ВЫСОТЫ ГРАНИТНОЙ СТЕНЫ
Длина тени дерева равна 10,2 м, а длина тени человека, рост которого 1,7 м, равна 2,5 м. Найдите высоту дерева. ЗАДАЧА №580 D E A B C
Для определения высоты дерева можно использовать зеркало так, как показано на рисунке. Луч света FD, отражаясь от зеркала в точке D, попадает в глаза человека ( точку В). Определите высоту дерева, если АС = 165 см, ВС = 12 см, АD = 120 см, DЕ =4,8 м, 1 = 2. ЗАДАЧА №581
На рисунке показано, как можно определить ширину ВВ1 реки, рассматривая два подобных треугольника. Определите ширину реки, если АС = 100м, АС1 = 32м, АВ1 = 34м. ЗАДАЧА №583 В1 В C1 C A
№ 1. Человек ростом 1,7 м стоит на некотором расстоянии от столба, на котором висит фонарь на высоте 5,1 м, при этом длина его тени – 10 м. Найдите расстояние от человека до фонаря (в метрах). № 2. Проектор полностью освещает экран А высотой 90 см, расположенный на расстоянии 240 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран В высотой 180 см, чтобы он был полностью освещен, если настройки проектора останутся неизменными. № 582. ДОМАШНЕЕ ЗАДАНИЕ
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-1457872
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
СК предложил обучать педагогов выявлять деструктивное поведение учащихся
Время чтения: 1 минута
В Башкирии школьные каникулы продлили до 14 ноября
Время чтения: 1 минута
Роспотребнадзор продлил действие санитарных правил для школ
Время чтения: 1 минута
В Воронежской области ввели масочный режим в школах
Время чтения: 2 минуты
Жириновский предложил ввести в школах уроки полового воспитания
Время чтения: 1 минута
Кабмин утвердил список вузов, в которых можно получить второе высшее образование бесплатно
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
№581. Для определения высоты дерева можно использовать зеркало так, как показано на рисунке 203
№579. Для определения высоты столба A1C1, изображенного на рисунке 199, использован шестПодробнее
Измерение высоты дереваПодробнее
№580. Длина тени дерева равна 10,2 м, а длина тени человека, рост которого 1,7 м, равнаПодробнее
Геометрия 8 класс. Задача № 581Подробнее
№583. На рисунке 204 показано, как можно определить ширину ВВ1 реки, рассматривая дваПодробнее
Номер 581 Геометрия 7 9 класс АтанасянПодробнее
Определение высоты сооруженияПодробнее
Определение высоты столбаПодробнее
2,4 дерево определение, оценка высотыПодробнее
География 5-6к. (28 параграф + итог 7 темы) Урок-практикумПодробнее
Геометрия Найдите высоту дерева, если длина его тени равна 8,4 м, а длина тени от вертикальногоПодробнее
География 5-6к. (30 параграф) + Итог 8 темы Урок-практикумПодробнее
Находим значение на графике функцииПодробнее
№582. Для определения расстояния от точки А до недоступной точки В на местности выбрали точку СПодробнее
Сваи в ЛИРА-САПР. КЭ-57 и ручной расчет.Подробнее
Для определения высоты дерева можно использовать зеркало так, как показано на рисунке. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека (точку В). Определите высоту дерева, если АС= 165 см, ВС= 12 см, AD=120 см, DE = 4,8 м, ∠1=∠2.
тр.EFD (по двум углам) и
отсюда EF=153*4=612см.
Ответ: 612см.
Найдем скалярное произведение векторов:
Найдем длины векторов:
|a| = √( ax ² + ay ² + az ²) = √( 1 ² + 1 ² + (-2) ²) = √(1 + 1 + ) = √6
|b| = √ bx ² + by ² + bz ² = √( (-3) ² + 3 ² + (-1) ²) = √(9 + 9 + 1) = √19
Найдем угол между векторами:
cos α = ( a · b) |a||b
| cos α = 2 /( √6*√19) = 2/ √114 ≈ 0.187317.
Ответ: 7. AB=BC=14 см или AB=BC=24 см, AC = 14 cм или AC = 32 см
Объяснение:
Периметр треугольника равен сумме длин всех его сторон.
AB=BC (по свойству равнобедренного треугольника)
Возьмём два случая
1 случай. AB=BC (по свойству равнобедренного треугольника), AB=BC=14см, значит сторона AC равна PΔABC-(AB+BC)
2 случай. AC = 14 cм, а AB=BC возьмём за x, получаем равенство: