если диск вращается вокруг неподвижной оси так что его угловая координата определяется уравнением
Диск радиусом 10 см вращается вокруг неподвижной оси так, что его угловая координата определяется уравнением φ = А + Вt+ Сt2+Dt3, где В = 1 рад/с, С = 1 рад / с2, D= 1 рад/с3.






Описание и исходные данные задания, 50% решения + фотография:
Диск радиусом 10 см вращается вокруг неподвижной оси так, что его угловая координата определяется уравнением φ = А + Вt+ Сt2+Dt3, где В = 1 рад/с, С = 1 рад / с2, D= 1 рад/с3. Определите для точек на ободе диска к концу второй секунды после начала движения: 1) тангенциальное ускорение aт; 2) нормальное ускорение an; 3) полное ускорение a.
Дано: φ= A+Вt+Сt2+Dt3 B=1 рад/с, C=1 рад/с2, D=1 рад/с3 t=2 c R=10 см=0,1 м
Нормальная составляющая ускорения аn: Угловая скорость по определению Найдем первую производную от : Для момента времени t=2 c.
Я и моя команда оказывает помощь в учёбе по любым предметам и заданиям любой сложности.
Решение задач является неотъемлемой частью обучения в любом учебном заведении, и я смогу помочь в решение задач по любым предметам.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Если диск вращается вокруг неподвижной оси так что его угловая координата определяется уравнением
Условие и решение задач
1. Координата x движущейся частицы меняется позакону x = A cos(2pt/T), А= 8 см. Найти выражения для проекций на ось x скорости v и ускорения a частицы, составляющую vx средней скорости частицы на интервале времени от t1 = 0 до t2= T/8.
→ Перейти к решению задачи
4. Радиус-вектор,определяющий положение движущейся частицы меняется по закону r =3t 2 i + 2t j + k, где i, j, k орты осей x, y, z. Найти модуль скорости v в момент времени t = 1 с.
→ Перейти к решению задачи
7. В момент t = 0 частица вышла из начала координат в положительном направлении оси х. Ее скорость меняется со временем по закону v = v0 (1 — t/τ), где v0 — вектор начальной скорости, модуль которого v0=10,0 см/с, τ = 5,0 с. Найти координату x частицы в моменты времени 6,0, 10 и 20 с.
→ Перейти к решению задачи
10. Материальная точка движется в плоскости x0y по закону x = Asinwt,y = A(1+coswt),где A и w положительные константы. Найдите уравнение кривой, описывающей траекторию частицы, изобразите ее вид и направление движения частицы.
→ Перейти к решению задачи
12. С вышки бросили камень в горизонтальном направлении. Через t=4 с камень упал на землю на расстоянии L = 40 м от основания вышки. Определите начальную v0 и конечную vf скорости камня.
→ Перейти к решению задачи
13. Камень брошен со скоростью v0 = 30 м/с под углом 60 0 кгоризонту. Определите радиус кривизны траектории в верхней ее точке.
→ Перейти к решению задачи
14. Шарик падает с нулевой начальной скоростью на гладкую наклонную плоскость, составляющую угол α с горизонтом. Пролетев расстояние h, он упруго отражается от плоскости. На каком расстоянии от места падения шарик отразится второй раз?
→ Перейти к решению задачи
15. На гладкую горизонтальную плоскость помещены три тела массами т1, т2 и т3,связанные нитями между собой и с телом массой М, привязанное к нити, перекинутой через блок. Найтиускорение а системы. Найти натяжениявсех нитей. Трением в блоке, массами блоков и нитей пренебречь.
→ Перейти к решению задачи
17. Движущаяся частица претерпевает упругое соударение с покоящейся частицей такой же массы. Доказать, что после столкновения, если оно не было центральным, частицы разлетятся под прямым углом друг к другу. Как будут двигаться частицы после центрального соударения?
→ Перейти к решению задачи
20. Диск вращается вокруг неподвижной оси так, что его координата определяется уравнением φ = 0,5t 2 (рад). Найдите касательное ускорение его точек, отстоящих от оси вращения на 80 см.
→ Перейти к решению задачи
22. Частица движется по окружности радиусом 2 см, при этом зависимость ее пути от времени задана уравнением s = 0,1 t 3 (см). Найдите касательное ускорение частицы в тот момент времени, когда ее линейная скорость стала 0,3 м/с.
→ Перейти к решению задачи
24. Нормальное ускорение частицы, движущейся по окружности радиусом 4 м, задается уравнением аn = 1 + 6t + 9t 2 (м/с 2 ). Вычислите касательное ускорение частицы через 1 с после начала движения.
→ Перейти к решению аналогичной задачи
25. Диск вращается вокруг неподвижной оси так, что его угловая координата определяется уравнением φ = 0,5 t 2 (рад). Вычислите полное ускорение точек, отстоящих от оси вращения на 80 см к концу второй секунды движения.
→ Перейти к решению задачи
26. Колесо радиусом 10 см вращается так, что линейная скорость точек на его ободе задана уравнением v= 3t+ t 2 (см/с)Найдите угол между вектором полного ускорения и радиусом колеса спустя 1 с после начала движения.
→ Перейти к решению задачи
35. Модуль импульса частицы массой 2 кг изменяется по закону р = 10 Cos πt (кгм/с). В начальный момент времени радиус-вектор частицы равен нулю. Найдите модуль радиус-вектора частицы через 1/3 секунды.
→ Решение отсутствует / Предложить свой вариант решения
36. Если путь частицы массой 2кг изменяется по закону s = 5 Sin πt (см). Найдите ближайший момент времени от начала еедвижения, когда модуль импульса частицы становится максимальным.
→ Перейти к решению задачи
38. Частица массой 1 кг в начальный момент времени имеет радиус-вектор r0 = 2 i+ 3 j, где i, j орты осей x, y. На нее действует сила F= 1,5y 2 i+ 3x 2 j – 0,2(x 2 +y 2 )k. Найдите модуль этой силы в начальный момент времени.
→ Перейти к решению задачи
39. Десять шариков массами 100 г, 200 г, …,1000 г укреплены в указанном порядке на невесомом стержне длиной 90 см. На каком расстоянии от центра самого легкого шарика будет находиться центр масс системы, если расстояние между соседними шариками 10 см?
→ Перейти к решению задачи
40. В двух вершинах равностороннего треугольника помещены шарики с массами m каждый, а в третьей вершине – с массой 2m. Где будет находиться центр масс данной системы.
→ Перейти к решению задачи
41. Автобус массой 5 т начинает двигаться от остановки так, что его скорость в зависимости от пройденного пути изменяется по закону v = √ s (м/с). Найдите суммарную работу всех сил, действующих на автобус за первые 15 с от начала движения.
→ Перейти к решению задачи
42. Воздушный поток (ρ = 1,29 кг/м 3 ) сечением 0,55 м 2 имеет скорость 20м/с. Чему будет равна мощность этого потока?
→ Перейти к решению задачи
44. Шар массой 2 кг движется со скоростью 8 м/с и догоняет шар массой 3 кг, который движется со скоростью 4 м/с. Найдите работу деформации шаров при их центральном неупругом ударе.
→ Решение отсутствует / Предложить свой вариант решения
45. В боковой поверхности сосуда с жидкостью,стоящего на горизонтальной плоскости, имеется малое отверстие. Высота неизменного уровня жидкости над этим отверстием составляет 36 см, а расстояние от отверстия до дна сосуда 144 см. Найдите дальность горизонтального полета струи жидкости из этого отверстия.
→ Решение отсутствует / Предложить свой вариант решения
49. Материальная точка движется в плоскости x0y по закону x = Asinwt,y = Bcoswt,где A, B и w положительные константы, A = B = 5 cм. Найдите уравнение кривой,описывающей траекторию частицы, изобразите ее вид и направление движения частицы.
→ Перейти к решению задачи
50. Материальная точка движется по дуге окружности радиуса R по закону L = A sinwt,где L смещение из начального положения, отсчитываемое вдоль дуги, A и w положительные константы. Найдите полное ускорение частицы в точке L = 0.
→ Перейти к решению задачи
55. Частица движется по окружности радиуса R = 15см с постоянным тангенциальным ускорением at. Найдите это ускорение, еслиизвестно, что к концу пятого оборота после начала движения скорость частицы стала равной v = 79.2 см/с.
→ Перейти к решению задачи
57. Найти работу, которую нужно совершить, чтобы увеличить скорость движения тела от v1= 2 м/с до v2= 6 м/с на пути s = 15 м. На всем пути действуетпостоянная сила трения Fтр=2 Н. Масса тела m = 1 кг.
→ Перейти к решению задачи
58. Находясь под действием постоянной силы с компонентами (3, 10, 8) Н частица переместилась из точки 1 с координатами (1, 2, 3) м в точку 2 с координатами (3, 2, 1) м. Какая совершилась при этом работа? Как изменилась кинетическая энергия частицы?
→ Перейти к решению задачи
60. Лодка длиной L0 наезжает,двигаясь по инерции, на отмель и останавливается из-за трения, когда половина ее длины оказывается на суше. Какова была начальная скорость лодки v? Коэффициент трения равен μ.
→ Решение отсутствует / Предложить свой вариант решения
61. Лодка массы М с находящимся в ней человеком массы т неподвижно стоит на спокойной воде. Человек начинает идти вдоль по лодке со скоростью u относительно лодки. С какой скоростью w будет двигаться человек относительно воды? С какой скоростью v будет при этом двигаться лодка относительно воды? Сопротивление воды движению лодки не учитывать.
→ Перейти к решению задачи
62. Человек прошел вдоль по лодке, описанной в предыдущей задаче, путь l. Каковы при этом будут смещения лодки S1 и человека S2 относительно воды?
→ Перейти к решению задачи
63. Две пружины жесткостью 4×10 2 Н/м и 6×10 2 Н/м соединены последовательно. Определить работу по растяжению обеих пружин, если вторая пружина растянута на 3 см. Определить также коэффициент жесткости системы двух пружин.
→ Перейти к решению задачи
64. Математический маятник (груз малых размеров налегком подвесе длиной l) находится вположении равновесия. Определить какую минимальную скорость u надо сообщить грузу, чтобы он мог совершить полный оборот, для двух случаев: а) груз подвешен на жестком стержне; б) на нити.
→ Перейти к решению задачи
65. Два идеально упругих шарика массами m1 и m2 вдоль одной и той же прямой со скоростями v1 и v2. Во время столкновения шарики начинают деформироваться, и часть кинетической энергии переходит в потенциальную энергию деформации. Затем деформация уменьшается, и запасенная потенциальная энергия вновь переходит в кинетическую. Найти значение потенциальной энергии деформации в момент, когда она максимальна.
→ Перейти к решению задачи
67. Два шарика падают в воздухе. Шарики сплошные, сделаны из одного материала, но диаметр одного из шариков вдвое больше другого. В каком соотношении будут находиться скорости шариков при установившемся (равномерном) движении? Считать, что сила сопротивления воздуха пропорциональна площади поперечного сечения движущегося тела и квадрату его скорости.
→ Перейти к решению задачи
70. Железный шарик (ρ = 7900 кг/м 3 ) диаметром 5 мм падает в касторовом масле ( ρ = 900 кг/м 3 | ŋ = 1 Пас). Вычислите число Рейнольдса при установившемся движении шарика.
→ Перейти к решению задачи
| 🎓 Заказ №: 21947 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Решение Уравнение для угловой скорости движения по окружности получается из заданного уравнения движения дифференцированием по времени. 2 B 2Ct 3Dt dt d (1) Связь между линейной и угловой скоростью имеет вид: R (2) Подставим (1) в (2): B Ct Dt R 2 2 3 (3) Производная от линейной скорости по времени дает выражение для модуля тангенциального ускорения.
Готовые задачи по физике которые сегодня купили:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Если диск вращается вокруг неподвижной оси так что его угловая координата определяется уравнением
вращается вокруг неподвижной оси
Сравните кинетическую энергию диска, вращающегося вокруг неподвижной оси и катящегося по горизонтальной плоскости. Линейная скорость точек на ободе диска одинакова.
Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = At 2 (А = 0,5 рад/с 2 ). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное аτ, нормальное аn и полное а ускорения.
Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = At 2 (А = 0,1 рад/с 2 ). Определите полное ускорение а точки на ободе диска к концу второй секунды после начала движения, если линейная скорость той точки в этот момент равна 0,4 м/с.
Сплошной шар диаметром 20 см и массой 35 кг вращается вокруг неподвижной оси, проходящей через его центр, с частотой 5 об/с. На шар подействовал постоянный вращающий момент, вследствие чего шар сделал 200 об за 15 с. Найти величину вращающего момента.
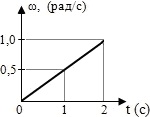
Маховик вращается вокруг неподвижной оси по закону, представленному на графике. Вращающий момент равен 10 Н·м. Определить момент инерции маховика.
| 🎓 Заказ №: 21911 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Решение Уравнение для угловой скорости движения по окружности получается из заданного уравнения движения дифференцированием по времени. 2 B 2Ct 3Dt dt d (1) Связь между линейной и угловой скоростью имеет вид: R (2) Подставим (1) в (2): B Ct Dt R 2 2 3 (3) Производная от линейной скорости по времени дает выражение для модуля тангенциального ускорения. DR RDt dt d a 2 6 (4) Скорость движения по окружности связана с нормальным ускорением соотношением: R an 2 (5)

Готовые задачи по физике которые сегодня купили:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института