если дискриминант отрицательный в неравенстве что делать

Дискриминант

Дискриминантом квадратного трехчлена называют выражение \(b^<2>-4ac\), где \(a, b\) и \(c\) – коэффициенты данного трехчлена.

Например, для трехчлена \(3x^2+2x-7\), дискриминант будет равен \(2^2-4\cdot3\cdot(-7)=4+84=88\). А для трехчлена \(x^2-5x+11\), он будет равен \((-5)^2-4\cdot1\cdot11=25-44=-19\).

Дискриминант и корни квадратного уравнения

Значение дискриминанта показывает количество корней квадратного уравнения:
— если \(D\) положителен – уравнение будет иметь два корня;
— если \(D\) равен нулю – только один корень;
— если \(D\) отрицателен – корней нет.

Если дискриминант положителен

В этом случае корень из него – это некоторое положительное число, а значит \(x_<1>\) и \(x_<2>\) будут различны по значению, ведь в первой формуле \(\sqrt\) прибавляется, а во второй – вычитается. И мы имеем два разных корня.

Пример: Найдите корни уравнения \(x^2+2x-3=0\)
Решение:

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Найдем корни уравнения

Получили два различных корня из-за разных знаков перед \(\sqrt\)

Если дискриминант равен нулю

А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.

То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.

Пример: Найдите корни уравнения \(x^2-4x+4=0\)
Решение:

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Находим корни уравнения

Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.

Если дискриминант отрицателен

В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.

Пример: Найдите корни уравнения \(x^2+x+3=0\)
Решение

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Находим корни уравнения

Оба корня содержат невычислимое выражение \(\sqrt<-11>\), значит, и сами не вычислимы

То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение \(x^2+x+3\) получился ноль.

Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.

Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!

Источник

Метод интервалов, решение неравенств

Определение квадратного неравенства

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

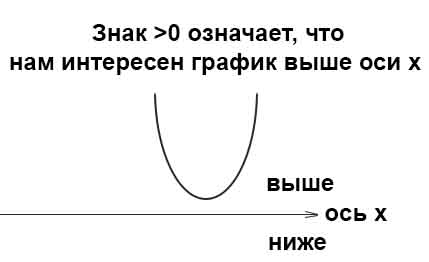
Квадратное неравенство выглядит так:

Квадратное неравенство можно решить двумя способами:

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Неравенство примет вид:

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Источник

Неравенства. Квадратные неравенства.

Квадратными неравенствами обозначают неравенства типа

В результате можем иметь нижеследующие варианты:

1) При D = 0 у квадратного уравнения один корень:

.

2) При D>0 у квадратного уравнения два корня. Парабола пересекает ось х в двух точках с абсциссами:

Если необходимо указать отрезок, на котором квадратный трехчлен положителен, то это отрезок расположен там, где парабола расположена над осью x. По аналогии если необходимо найти отрицательные значения, то берем отрезок, где парабола расположена под осью x

При решении неравенства ax 2 +bx +c > 0 не требуется тщательно строить параболу у= ax 2 +bx +c по точкам (к примеру, вовсе нет необходимости вычислять вершину параболы, точку пересечения с осью у и т. д.). Допустимо упрощенно изобразить кривую. Точность необходима только при вычислении корней уравнения ax 2 +bx +c=0 (при D > 0).

Источник

Квадратные неравенства

Чтобы решить квадратные неравенства вспомним, что такое квадратичная функция?
Квадратичная функция – это функция записанная формулой : y=ax 2 +bx+c, где x – независимая переменная, a, b и c – некоторые числа, при этом a≠0.
Графиком квадратичной функции является парабола.

В зависимости от значения a ветви графика направлены вверх или вниз:

Квадратные неравенства имеют вид.

ax 2 +bx+c>0
ax 2 +bx+c 2 +bx+c≥0
ax 2 +bx+c≤0

Чтобы начать решать квадратные неравенства, необходимо знать как решаются квадратные уравнения?
А также для графического метода решения неравенства, необходимо знать алгоритм построения квадратичной функции или параболы?

Как решать квадратные неравенства?

Решение квадратных неравенств рассмотрим на примерах. Для начала разберем случаи, когда у квадратного уравнения дискриминант меньше нуля (нет корней).

Пример:

Дискриминант меньше нуля —236, следовательно у уравнения нет корней, а это значит, что весь график параболы находится выше оси х, потому что а=3>0 (ветви параболы смотрят вверх)

Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x 2 +2x+20>0.

Получили верное неравенство 25>0, следовательно так как у нас нет корней уравнения нам подойдут все точки числовой прямой.

Пример:

Рассмотрим этот же пример со знаком неравенства меньше 0

Дискриминант меньше нуля —236, следовательно у уравнения нет корней, значит парабола не пересекает ось x. Весь график параболы находится выше оси х, потому что а=3>0.

А знак уравнения меньше 2 +2x+20 2 +2•1+20 2 +x-2 2 +x-2=0

Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.

Знак уравнения меньше 2 +x-2 2 +(-3)-2 2 +(0)-2 2 +(2)-2 2 +x-2>0

Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.

Знак уравнения больше >0. Нам в ответ необходимо записать часть параболы, которая находится выше оси x. Визуально графически можно оценить по картинке, нам подходят интервалы (-∞;-2) и (1;+∞).

Также можно решить методом интервалов. Ось x делится на три участка.

Получили верное неравенство 4>0, следовательно этот интервал (-∞; 2) подходит.

Второй участок (-2; 1). На этом участке можно взять число 0.

Третий участок (1; +∞). На этом участке возьмем число 2.

Получили верное неравенство 4>0, следовательно этот интервал (1; +∞) подходит.

Источник

Квадратные неравенства.
Метод интервалов

Прежде чем разбираться, как решать квадратное неравенство, давайте рассмотрим, какое неравенство называют квадратным.

Неравенство называют квадратным, если старшая (наибольшая) степень неизвестного « x » равна двум.

Потренируемся определять тип неравенства на примерах.

Как решить квадратное неравенство

В предыдущих уроках мы разбирали, как решать линейные неравенства. Но в отличие от линейных неравенств квадратные решаются совсем иным образом.

Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.

Что такое метод интервалов

Методом интервалов называют специальный способ решения квадратных неравенств. Ниже мы объясним, как использовать этот метод и почему он получил такое название.

Чтобы решить квадратное неравенство методом интервалов нужно:

Мы понимаем, что правила, описанные выше, трудно воспринимать только в теории, поэтому сразу рассмотрим пример решения квадратного неравенства по алгоритму выше.

Требуется решить квадратное неравенство.

Переходим к п.2. Необходимо сделать так, чтобы перед « x 2 » стоял положительный коэффициент. В неравенстве « x 2 + x − 12 » при « x 2 » стоит положительный коэффициент « 1 », значит, снова нам ничего делать не требуется.

Согласно п.3 приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.

x_1;2 =

x_1;2 =

x_1;2 =

Теперь по п.4 отметим полученные корни на числовой оси в порядке возрастания.

Помните, что, исходя их того, какое перед нами неравенство (строгое или нестрогое) мы отмечаем точки на числовой оси разным образом.

Теперь, как сказано в п.5, нарисуем «арки» над интервалами между отмеченными точками.

Проставим знаки внутри интервалов. Справа налево чередуя, начиная с « + », отметим знаки.

Нам осталось только выполнить пункт 6, то есть выбрать нужные интервалы и записать их в ответ. Вернемся к нашему неравенству.

Запишем полученный ответ квадратного неравенства.

Именно из-за того, что при решении квадратного неравенства мы рассматриваем интервалы между числами, метод интервалов и получил свое название.

После получения ответа имеет смысл сделать его проверку, чтобы убедиться в правильности решения.

Выберем любое число, которое находится в заштрихованной области полученного ответа −4 и подставим его вместо « x » в исходное неравенство. Если мы получим верное неравенство, значит мы нашли ответ квадратного неравенства верно.

Возьмем, например, из интервала число « 0 ». Подставим его в исходное неравенство « x 2 + x − 12 ».

Мы получили верное неравенство при подстановке числа из области решений, значит ответ найден правильно.

Краткая запись решения методом интервалов

Сокращенно запись решения квадратного неравенства методом интервалов будет выглядеть так:

x 2 + x − 12 2 + x − 12 = 0

x_1;2 =

x_1;2 =

Ответ: −4

Другие примеры решения квадратных неравенств

Рассмотрим решение других примеров квадратных неравенств. Требуется решить квадратное неравенство:

В правой части неравенство уже стоит ноль. При « x 2 » стоит « 2 » ( положительный коэффициент), значит можно сразу переходить к поиску корней.

x_1;2 =

Ответ: x ≤ 0 ; x ≥

Рассмотрим пример, где перед « x 2 » в квадратном неравенстве стоит отрицательный коэффициент.

По п.2 общих правил решения методом интервалов нам нужно сделать так, чтобы перед « x 2 » стоял положительный коэффициент. Для этого умножим все неравенство на « −1 ».

Можно переходить к п.4 и п.5. Приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение. Затем расположим полученные корни на числовой оси и проведем между ними «арки».

x_1;2 =

x_1;2 =

0″ />

При определении того какие интервалы нам нужно брать в ответ, исходить нужно из самого последнего изменения неравенства перед нахождением его корней.

В нашем случае самая последняя версия неравенства перед поиском корней уравнения это « x 2 + 3x − 4 ≤ 0 ».

Значит для ответа нужно выбирать интервалы со знаком « − ».

0″ /> Ответ: −4 ≤ x ≤ 1

К сожалению, при решении квадратного неравенства не всегда получаются два корня и все идет по общему плану выше. Возможны случаи, когда получается один корень или даже ни одного корня.

Как решить квадратные неравенства в таких случаях, мы разберем в следующем уроке «Квадратные неравенства с одним корнем или без корней».

Источник