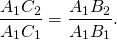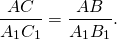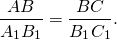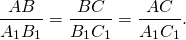если два угла одного треугольника соответственно равны двум углам другого треугольника то такие

Первый признак подобия треугольников

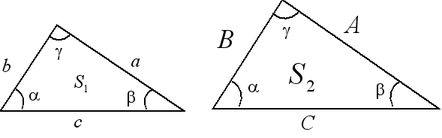
(Первый признак подобия треугольников — подобие треугольников по двум углам)

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Дано: ΔABC, ΔA₁B₁C₁,

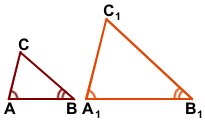
1) По теореме о сумме углов треугольника

2) На луче A₁B₁ отложим отрезок A₁B₂, A₁B₂=AB.

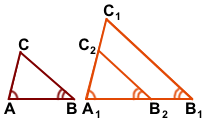
3) Через точку B₂ проведем прямую B₂C₂, параллельную прямой B₁C₁.

Из равенства треугольников следует равенство соответствующих сторон: A₁C₂=AC.

7) Аналогично доказывается, что

8) Таким образом, в треугольниках ABC и A₁B₁C₁:

Что и требовалось доказать.

При решении задач чаще других используется именно 1-й признак подобия треугольников.

Источник

Признаки равенства треугольников

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Источник

Если два угла одного треугольника соответственно равны двум углам другого треугольника то такие

Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его медианой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны» — верно по признаку подобия треугольников.

2) «Вертикальные углы равны» — верно, это теорема планиметрии.

3) «Любая биссектриса равнобедренного треугольника является его медианой» — неверно, это утверждение справедливо только для равностороннего треугольника.

Заметим, что признак подобия треугольников в учебнике геометрии сформулирован так: «если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны». В утверждении номер 1 опущено слово «соответственно», что не меняет сути.

Укажите номера верных утверждений.

1) Существует квадрат, который не является прямоугольником.

2) Если два угла треугольника равны, то равны и противолежащие им стороны.

3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Существует квадрат, который не является прямоугольником» — некорректное утверждение, корректное — «Существует прямоугольник, который не является квадратом».

2) «Если два угла треугольника равны, то равны и противолежащие им стороны» — верно, т. к. треугольник, два угла которого равны является равнобедренным, причём равные стороны лежат напротив равных углов.

3) «Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны» — верно, это теорема планиметрии.

Укажите номера верных утверждений.

1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

2) В любом прямоугольнике диагонали взаимно перпендикулярны.

3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части» — верно по свойству равнобедренного треугольника.

2) «В любом прямоугольнике диагонали взаимно перпендикулярны» — неверно, это утверждение справедливо только для прямоугольника, у которого все стороны равны, то есть для квадрата.

3) «Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу» — верно, т. к. окружность — множество точек, находящихся на заданном расстоянии от данной точки.

Источник

Признаки равенства и подобия треугольников

Признаки равенства треугольников

Равными называют треугольники, у которых соответствующие стороны равны.

Теорема (первый признак равенства треугольников).
Если две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу, заключенному между ними, другого треугольника, то такие треугольники равны.

Теорема (второй признак равенства треугольников).
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Теорема (третий признак равенства треугольников).
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Признаки подобия треугольников

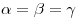
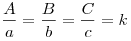
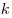
Подобными называются треугольники, у которых углы равны, а сходственные стороны пропорциональны: , , где — коэффициент подобия.

I признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны.

II признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

III признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Следствие: Площади подобных треугольников относятся как квадрат коэффициента подобия: .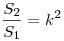

Источник

Треугольник.

Треугольником называется геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки, образующие треугольник, называются сторонами треугольника, а их общие концы — вершинами треугольника.

Площадь треугольника через сторону и высоту, проведенную к этой стороне:

Площадь треугольника через радиус вписанной окружности и полупериметр :

Площадь треугольника через радиус вневписанной окружности и полупериметр:

Площадь треугольника через радиусы вневписанных окружностей и радиус вписанной окружности:

Площадь треугольника через радиус описанной окружности и стороны:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через высоту и сторону:

Площадь треугольника через длины сторон и полупериметр (формула Герона):

Интересная теорема об отношении площадей треугольников, имеющих равный угол:

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Замечательные точки треугольника

Инцентр треугольника — точка пересечения биссектрис треугольника. Инцентр является центром вписанной окружности.

Центроид треугольника — точка пересечения медиан треугольника.

Ортоцентр треугольник — точка пересечения прямых, содержащих высоты треугольника.

Про другие замечательные точки и прямые треугольника вы можете прочитать здесь.

Источник