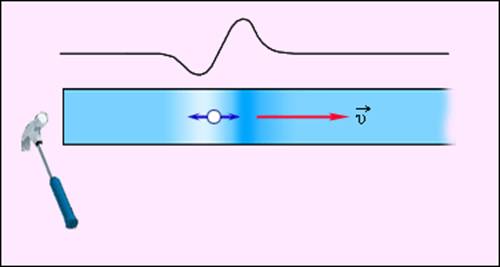
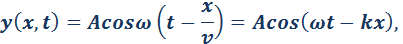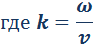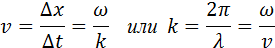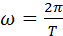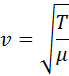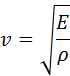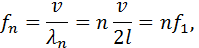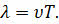если колебания происходят вдоль направления распространения волны то такая волна называется
Механические волны
1.В каких направлениях совершается колебание частиц среды в продольной волне?
А. Во всех направлениях
Б. Только по направлению распространения волны.
В. Только перпендикулярно направлению распространения волны.
2. По поверхности озера распространяется волна со скоростью 4,2 м/с. Какова частота колебания бакена, если длина волны 3 м?
А. 1,4 Гц. Б. 2,4 Гц. В. 3,4 Гц.
3.Человек, стоящий на берегу, определил, что расстояние между следующими друг за другом гребнями волн 8 м и за одну минуту мимо него проходит 45 волновых гребней. Определите скорость расстояния волн.
А. 12 м/с. Б. 10 м/с. В. 6 м/с.
4.От чего зависит скорость распространения волны?
А. От вида веществ и его состояния.
В. От длины волны л.
5. Если колебания происходят вдоль направления распространения волны, то такая вона называется:
6. Какие волны возникают в воздушном столбе внутри духовой трубы, когда музыкант дует в трубу?
7.Волны, возбуждаемые смычком в струне, являются:
8. Какие из поперечных свойств относятся к механическим волнам?
А. Волны переносят энергию.
Б. Волны переносят вещество.
В. Источником волн являются колеблющиеся тела.
9. Какие из перечисленных свойств относятся к продольным волнам?
А. Эти волны могут распространяться только в газах.
Б. Частицы среды при колебаниях смещаются вдоль направления распространения волны.
В. Эти волны представляют собой чередующиеся разряжения и сжатия.
10. Продольные волны могут распространяться
1. В каких направлениях совершаются колебание частиц среды в поперечной волне?
А. Во всех направлениях.
Б. Только по направлению распространения волны.
В. Только перпендикулярно направлению распространения волны.
2. Лодка качается на волнах, распространяющихся со скоростью 2,5 м/с. Расстояние между двумя ближайшими гребнями волн 10 м. Определите частоту колебаний лодки.
А. 0,5 Гц. Б. 0,25 Гц. В. 1,5 Гц.
3. С какой скоростью распространяется волна, если за 20 с тоски волны совершили 50 колебаний? Длина волны равна 2 м.
А. 5м/с. Б. 2 м/с. В. 1м/с.
4. От чего зависит длина волны?
Б. От среды, в которой распространяется.
В. От частоты вибрации.
5. Если колебания происходят перпендикулярно направлению распространения волны, то такая волна называется:
6.Какие волны возникают в струнах при игре на гитаре?
7.Волны возбуждаемые смычком в воздухе, при игре на скрипке, является:
8. Какие из перечисленных свойств относятся к поперечным волнам?
А. Эти волны представляют собой чередующиеся сжатия и разрежения.
Б. Эти волны могут распространяться только в твердых телах.
В. В этой волне колебания совершаются перпендикулярно направлению распространения волны.
9. Колебания, распространяющиеся в пространстве с течением времени называются:
10. Поперечные волны могут распространяться
Если колебания происходят вдоль направления распространения волны то такая волна называется
Пусть колеблющееся тело находится в среде, все частицы которой связаны между собой. Соприкасающиеся с ним частицы среды придут в колебательное движение, в результате чего в прилегающих к этому телу участках среды возникают периодические деформации (например, сжатие и растяжение). При деформациях в среде появляются упругие силы, которые стремятся вернуть частицы среды в первоначальное состояние равновесия.
Таким образом, периодические деформации, которые появились в каком-нибудь месте упругой среды, будут распространяться с некоторой скоростью, зависящей от свойств среды. При этом частицы среды не вовлекаются волной в поступательное движение, а совершают колебательные движения около своих положений равновесия, от одних участков среды к другим передается только упругая деформация.
Процесс распространения колебательного движения в среде называется волновым процессом или просто волной. Иногда эту волну называют упругой, потому что она обусловлена упругими свойствами среды.
В зависимости от направления колебаний частиц по отношению к направлению распространения волны, различают продольные и поперечные волны. Интерактивная демонстрация поперечной и продольной волны
Продольная волна – это волна, в которой частицы среды колеблются вдоль направления распространения волны.
Продольную волну можно наблюдать на длинной мягкой пружине большого диаметра. Ударив по одному из концов пружины, можно заметить, как по пружине будут распространяться последовательные сгущения и разрежения ее витков, бегущие друг за другом. На рисунке точками показано положение витков пружины в состоянии покоя, а затем положения витков пружины через последовательные промежутки времени, равные четверти периода.
Рассмотрим подробнее процесс образования поперечных волн. Возьмем в качестве модели реального шнура цепочку шариков (материальных точек), связанных друг с другом упругими силами. На рисунке изображен процесс распространения поперечной волны и показаны положения шариков через последовательные промежутки времени, равные четверти периода.
В начальный момент времени (t0 = 0) все точки находятся в состоянии равновесия. Затем вызываем возмущение, отклонив точку 1 от положения равновесия на величину А и 1-я точка начинает колебаться, 2-я точка, упруго связанная с 1-й, приходит в колебательное движение несколько позже, 3-я — еще позже и т.д. Через четверть периода колебания ( t 2 = T 4 ) распространятся до 4-й точки, 1-я точка успеет отклониться от своего положения равновесия на максимальное расстояние, равное амплитуде колебаний А. Через половину периода 1-я точка, двигаясь вниз, возвратится в положение равновесия, 4-я отклонилась от положения равновесия на расстояние, равное амплитуде колебаний А, волна распространилась до 7-й точки и т.д.
Демонстрация распространения поперечной волны
Вид волны зависит от вида деформации среды. Продольные волны обусловлены деформацией сжатия — растяжения, поперечные волны — деформацией сдвига. Поэтому в газах и жидкостях, в которых упругие силы возникают только при сжатии, распространение поперечных волн невозможно. В твердых телах упругие силы возникают и при сжатии (растяжении) и при сдвиге, поэтому в них возможно распространение как продольных, так и поперечных волн.
Как показывают рисунки, и в поперечной и в продольной волнах каждая точка среды колеблется около своего положения равновесия и смещается от него не более чем на амплитуду, а состояние деформации среды передается от одной точки среды к другой. Важное отличие упругих волн в среде от любого другого упорядоченного движения ее частиц заключается в том, что распространение волн не связано с переносом вещества среды.
Следовательно, при распространении волн происходит перенос энергии упругой деформации и импульса без переноса вещества. Энергия волны в упругой среде состоит из кинетической энергии совершающих колебания частиц и из потенциальной энергии упругой деформации среды.
Механические волны
Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.
Механические волны бывают разных видов. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.
Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной. Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.
Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.
Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.
Распространение поперечного волнового импульса по натянутому резиновому жгуту
Распространение продольного волнового импульса по упругому стержню
Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами. В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной модели твердое тело можно представить как совокупность шариков и пружинок (рис. 2.6.3).
Простейшая одномерная модель твердого тела
В этой модели инертные и упругие свойства разделены. Шарики обладают массой m, а пружинки – жесткостью k. С помощью такой простой модели можно описать распространение продольных и поперечных волн в твердом теле. В продольных волнах шарики испытывают смещения вдоль цепочки, а пружинки растягиваются или сжимаются. Такая деформация называется деформацией растяжения или сжатия. В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением.
Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
Продольные волны – это периодические сгущения и разрежения среды. Поэтому такие волны могут существовать в любых телах – твердых, жидких, газообразных. Поперечные волны могут существовать лишь в твердых телах. Это объясняется тем, что для распространения такой волны необходимо «жесткое» расположение частиц среды, чтобы между ними могли возникать силы упругости.
Если в одномерной модели твердого тела один или несколько шариков сместить в направлении, перпендикулярном цепочке, то возникнет деформация сдвига. Деформированные при таком смещении пружины будут стремиться возвратить смещенные частицы в положение равновесия. При этом на ближайшие несмещенные частицы будут действовать упругие силы, стремящиеся отклонить их от положения равновесия. В результате вдоль цепочки побежит поперечная волна.
В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появится. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах.
Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой f и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.
Смещение y (x, t) частиц среды из положения равновесия в синусоидальной волне зависит от координаты x на оси OX, вдоль которой распространяется волна, и от времени t по закону:
– так называемое волновое число, ω = 2πf – круговая частота.
На рис. 2.6.4 изображены «моментальные фотографии» поперечной волны в два момента времени: t и t + Δt. За время Δt волна переместилась вдоль оси OX на расстояние υΔt. Такие волны принято называть бегущими (в отличие от стоячих волн, см. далее).
«Моментальные фотографии» бегущей синусоидальной волны в момент времени t и t + Δt
Длиной волны λ называют расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за период Т, следовательно, λ = υT, где υ – скорость распространения волны.
Для любой выбранной точки на графике волнового процесса (например, для точки A на рис. 2.6.4) с течением времени t изменяется координата x этой точки, а значение выражения ωt – kx не изменяется. Через промежуток времени Δt точка A переместится по оси OX на некоторое расстояние Δx = υΔt. Следовательно:
Таким образом, бегущая синусоидальная волна обладает двойной периодичностью – во времени и пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны λ. Волновое число 
Обратим внимание на то, что уравнение
описывает синусоидальную волну, распространяющуюся в направлении, противоположном направлению оси OX, со скоростью 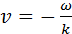
В бегущей синусоидальной волне каждая частица среды совершает гармонические колебания с некоторой частотой ω. Поэтому, как и в случае простого колебательного процесса, средняя потенциальная энергия, запасенная в некотором объеме среды, равна средней кинетической энергии в том же объеме и пропорциональна квадрату амплитуды колебаний.
Отсюда следует, что при распространении бегущей волны возникает поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.
Бегущие волны распространяются в средах с определенными скоростями, зависящими от типа волны, а также от инертных и упругих свойств среды.
Скорость поперечных волн в натянутой струне или резиновом жгуте зависит от погонной массы μ (т. е. массы единицы длины) и силы натяжения T:
Скорость распространения продольных волн в безграничной среде определяется плотностью среды ρ (т. е. массой единицы объема) и модулем всестороннего сжатия B, который равен коэффициенту пропорциональности между изменением давления Δp и относительным изменением объема ΔV / V, взятому с обратным знаком:
Выражение для скорости распространения продольных волн в безграничных средах имеет вид
Например, при температуре 20 °С скорость распространения продольных волн в воде υ ≈ 1480 м/с, в различных сортах стали υ ≈ 5–6 км/с.
При распространении продольных волн в упругих стержнях в формулу для скорости волн вместо модуля всестороннего сжатия B входит модуль Юнга E :
Для стали отличие E от B невелико, для других материалов оно может составлять 20–30 % и даже больше.
Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.
Если волны, бегущие по струне во встречных направлениях, имеют синусоидальную форму, то при определенных условиях они могут образовать стоячую волну.
Пусть струна длины l закреплена так, что один из ее концов находится в точке x = 0, а другой – в точке x1 = L (рис. 2.6.5). В струне создано натяжение T.
Образование стоячей волны в струне, закрепленной на обоих концах
По струне одновременно распространяются в противоположных направлениях две волны одной и той же частоты:
В точке x = 0 (один из закрепленных концов струны) падающая волна y1 в результате отражения порождает волну y2. При отражении от неподвижно закрепленного конца отраженная волна оказывается в противофазе с падающей. Согласно принципу суперпозиции, который является экспериментальным фактом, колебания, вызванные встречными волнами в каждой точке струны, складываются. Таким образом, результирующее колебание в каждой точке равно сумме колебаний, вызванных волнами y1 и y2 в отдельности. Следовательно,
Это и есть стоячая волна. В стоячей волне существуют неподвижные точки, которые называются узлами. Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями.
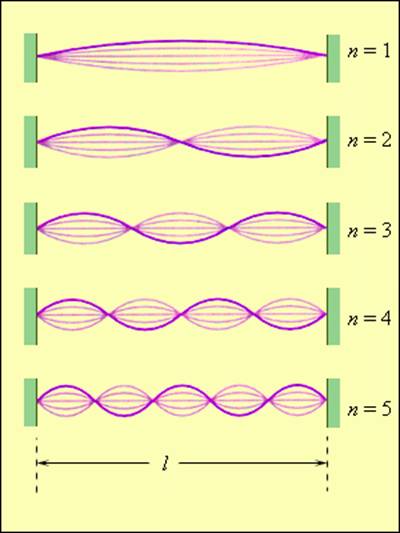
Оба неподвижных конца струны должны быть узлами. Приведенная выше формула удовлетворяет этому условию на левом конце (x = 0). Для выполнения этого условия и на правом конце (x = L), необходимо чтобы kL = nπ, где n – любое целое число. Это означает, что стоячая волна в струне возникает не всегда, а только в том случае, если длина L струны равняется целому числу длин полуволн:
Набору значений λn длин волн соответствует набор возможных частот fn:
где 
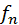
В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не транспортируется в другие части струны. В каждом таком отрезке происходит периодическое (дважды за период T) превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Но в отличие от груза на пружине или маятника, у которых имеется единственная собственная частота
струна обладает бесконечным числом собственных (резонансных) частот fn. На рис. 2.6.6 изображены несколько типов стоячих волн в струне, закрепленной на обоих концах.
Первые пять нормальных мод колебаний струны, закрепленной на обоих концах
В соответствии с принципом суперпозиции стоячие волны различных типов (т. е. с разными значениями n) могут одновременно присутствовать в колебаниях струны.
Волновые явления. Характеристики волны
Урок 17. Физика 11 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Волновые явления. Характеристики волны»
Помимо обычного колебательного движения в узкой области пространства, возможно ещё и распространение этих колебаний в среде. Вы знаете, что отдельные частицы любого тела — твёрдого, жидкого или газообразного — взаимодействуют друг с другом. Поэтому если какая-либо частица тела начинает совершать колебательные движения, то в результате взаимодействия между частицами это движение начинает с некоторой скоростью распространяться во все стороны.
Процесс распространения колебаний в пространстве с течением времени называется волновым процессом. А последовательное возникновение колебаний в точках, удалённых от источника, называется волной.
Наиболее отчётливо главные особенности волнового движения можно увидеть, если рассматривать волны на поверхности воды. Например, если мы бросим камень в воду, то в месте его падения по воде пойдут круги — это волны. Если на пути такой волны поместить поплавок, то он начнёт колебаться вверх-вниз, оставаясь при этом практически на месте. Из такого простого наблюдение вытекает одно из важнейших свойств волн: при возбуждении волны происходит процесс распространения колебаний, но не перенос вещества.
Колеблющееся тело, возбуждающее волновое движение частиц среды, называется источником волны или вибратором.
Механизм образования волны можно представить следующим образом. Источник колебаний (например, камертон) воздействует на частицы упругой среды, соприкасающиеся с ним, и заставляет их совершать вынужденные колебания. Среда вблизи источника деформируется, и в ней возникают силы упругости, препятствующие деформации. Если частицы среды сближаются, то возникающие силы их отталкивают, а если удаляются друг от друга, то, наоборот, притягивают. Постепенно силы будут действовать на все более удалённые от источника частицы среды, приводя их в колебательное движение. В результате оно будет распространяться в виде волны.
Механические волновые явления имеют огромное значение в повседневной жизни людей. К этим явлениям относится не только распространение звуковых колебаний, благодаря которым мы можем слышать на расстоянии. Мелкая рябь на поверхности озера и огромные океанские волны — это тоже механические волны, хотя и иного типа.
Мы будем рассматривать только бегущие волны. Их основное отличие от других волн заключается в том, что они, распространяясь в пространстве, переносят энергию без переноса вещества.
В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают два вида волн: продольные и поперечные.
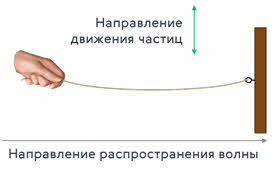
Поперечной называется волна, если частицы среды совершают колебания в направлении, перпендикулярном к направлению распространения волны.
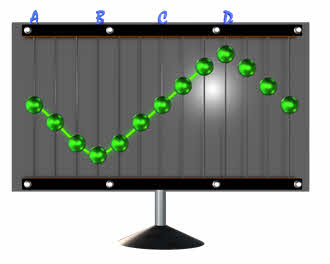
Рассмотрим подробнее процесс образования поперечных волн на примере волновой машины. В качестве колеблющихся частиц здесь выступают шарики, связанные друг с другом системой пружин (они спрятаны сзади). Источником колебаний будет выступать наша рука, вращающая рукоятку. Предположим, что вызванные нами колебания будут происходить вдоль оси игрек по гармоническому закону.
Обозначим буквами А, В, С и так далее частицы, отстоящие друг от друга на расстоянии в четверть периода, то есть на расстоянии, проходимом волной за одну четвёртую часть периода колебаний, совершаемых частицами. Будем считать, что волна распространяется вдоль оси икс слева направо. Заставим первую частицу двигаться вверх. Из-за возникающих сил упругости она потянет за собой остальные частицы. Однако на возникновение деформации и сил упругости потребуется некоторое время. Поэтому спустя четверть периода частица А достигнет своего крайнего верхнего положения. В этот момент своё движение вверх начнёт частица В. Спустя ещё четверть периода первая частица будет проходить положение равновесия, двигаясь в направлении сверху вниз. Частица В достигнет своего крайнего верхнего положения. И в этот момент начнёт своё движение вверх частица, обозначенная нами буквой С. Спустя ещё четверть периода первая частица закончит полный цикл колебания и будет находиться в таком же состоянии движения, как и в начальный момент. А вся волна к этому моменту времени, достигнет частицы D. Теперь все наши частицы расположены так, что образуют волну, состоящую из впадины и горба. В дальнейшем, благодаря силам взаимодействия каждая частица в цепочке будет повторять движение первой, но с некоторым запаздыванием, которое будет тем больше, чем дальше находится частица от источника волны.
Отметим, что поперечные волны возникают только в твёрдых телах, так как сдвиг слоёв относительно друг друга в газах и жидкостях не приводит к появлению сил упругости.
Но колебания частиц среды могут происходить не только перпендикулярно, но и вдоль направления распространения волны. Такие волны называются продольными.
Пронаблюдать закономерности продольных волн мы можем также на волновой машине, заставив шарики-частицы двигаться не вверх-вниз, а вправо-влево. Как видно, при прохождении продольной волны в среде создаются чередующиеся сгущения и разрежения частиц, перемещающиеся в направлении распространения волны с некоторой конечной скоростью.
Так как растягиваться и сжиматься может любая среда, то продольные механические волны могут распространяться в любых средах — твёрдых, жидких и газообразных.
На основании рассмотренных нами опытов мы можем сделать несколько очень важных выводов:
Во-первых, смещение каждой точки от положения равновесия происходит с течением времени периодически.
Во-вторых, смещения всех точек в каждый момент времени периодически изменяются от точки к точке, то есть являются периодической функцией координат.
А в-третьих, колебания частиц среды, в которой распространяется волна, являются вынужденными колебаниями, частота которых равна частоте колебаний источника волны.
Однако скорость распространения волны зависит от среды, в которой она распространяется. В основном это связано с тем агрегатным состоянием, в котором находится вещество. Напомним, что в твёрдых телах частицы расположены близко друг к другу и связь между ними велика. Следовательно, и скорость распространения волны в твёрдых телах будет самой высокой. В жидкостях частицы расположены дальше друг от друга и слабее взаимодействуют друг с другом. Поэтому скорость волн в них будет меньше, чем в твёрдых телах, но гораздо больше, чем в газах, так как в последних взаимодействие между частицами практически отсутствует.
Все время, пока существует волна, частицы среды совершают колебания около своих положений равновесия и смещаются от него не более чем на амплитуду. При этом различные частицы колеблются со сдвигом по фазе, за исключением тех, положения равновесия которых находятся друг от друга на расстоянии υТ. Так вот, расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны. Очевидно, что длина волны равна тому расстоянию, на которое распространяется волна за период:
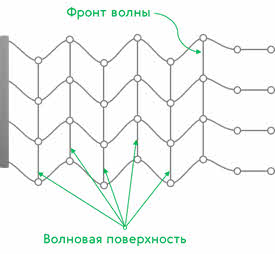
Необходимо помнить, что в действительности колеблются не только частицы, расположенные вдоль оси, а совокупность частиц, заключённых в некотором объёме. Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к данному моменту времени, называется фронтом волны (или волновым фронтом). Он представляет собой ту поверхность, которая отделяет часть пространства, уже вовлечённую в волновой процесс, от области, в которой колебания ещё не возникли
Геометрическое место точек, колеблющихся в одинаковой фазе, образуют волновую поверхность. Её можно провести через любую точку пространства, охваченного волновым процессом. Поэтому волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени только один. Кроме этого, волновой фронт всё время движется в то время, как волновые поверхности остаются неподвижными.
Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой систему параллельных друг другу плоскостей, перпендикулярных к направлению распространения волны. Такие волны можно получить на поверхности воды в плоской ванночке с помощью колебаний плоского стержня.
В сферической волне волновые поверхности представляют собой концентрические сферы. Такая волна распространяется с одинаковой скоростью по всем направлениям. Сферическую волну может создать пульсирующий в однородной упругой среде шар.
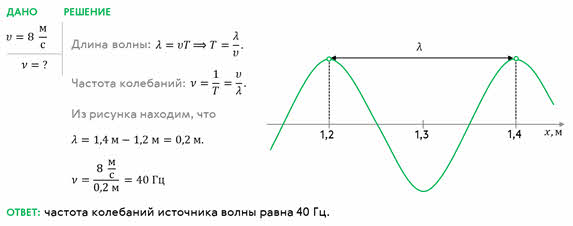
А теперь, для закрепления нового материала решим с вами такую задачу. На рисунке изображён участок натянутого резинового шнура, по которому распространяется поперечная волна со скоростью 8 м/с. Определите частоту колебаний её источника.
В заключение отметим, что некоторые волновые процессы, наблюдаемые в природе, нередко переносят огромную энергию и являются причиной разрушений. К ним, например, относятся морские волны и, особенно, цунами. А также сейсмические волны, распространяющиеся в земной коре при землетрясениях или мощных взрывах.