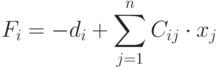если на каком либо шаге не удается отыскать ненулевой ведущий элемент то это значит

Компьютерное моделирование и решение линейных и нелинейных многомерных систем

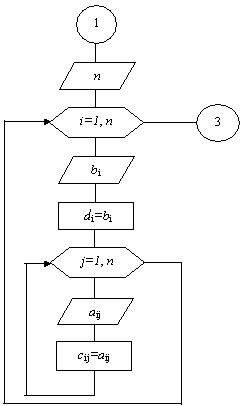
Блок 2. С помощью двух вложенных циклов с управляющими переменными i=1,n и j=1,k организуем ввод коэффициентов a_i,j и свободных членов b_i исходной системы. Для того, чтобы в дальнейшем можно было выполнить в блоке 9 проверку результата, в алгоритме предусмотрено сохранение значений a_i,j и b_i исходной системы с помощью переприсвоений: c_ij=a_ij и d_i=b_i

Блок 4. На каждом шаге прямого хода выполняем поиск ненулевого ведущего элемента.

Поиск ненулевого ведущего элемента ведётся в следующем порядке:

а) На каждом k-ом шаге прямого хода ведущий элемент каждой строки сравнивается с нулём;

б) Если в k-ой строке имеется нулевой ведущий элемент, то в k-ом столбце в цикле осуществляется поиск ненулевого элемента.

г) Если ненулевой ведущий элемент не найден, то коду ошибки kо присваиваем значение 1 и расчёт прекращается.

Если корни системы найдены, то F_i – это число, близкое к нулю.

Блок 9 в алгоритме метода Гаусса рекомендуется использовать только в процессе отладки метода.

В дальнейшем, при использовании метода Гаусса при решении различных прикладных задач, особенно в тех случаях, когда метод Гаусса используется внутри другого метода, блок 9 можно опустить, а в блоке 2 при вводе данных исходные значения коэффициентов системы и её свободных членов можно не сохранять.

Источник

Если на каком либо шаге не удается отыскать ненулевой ведущий элемент то это значит

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.

Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Система линейных уравнений вида (4.1) называется нормальной, если выполняются два следующих условия.

1. Матрица А коэффициентов при неизвестных симметрична, т.е.

2. Квадратичная форма U, соответствующая матрице А, n n U = ij j a xi x (4.49) i=1 j = положительно определена (т.е. принимает при любых значениях аргументов xi неотрицательные значения, причем обращается в нуль, только когда все аргументы xi равны нулю).

Если матрица коэффициентов А = [ aij ] неособенная (т.е. det A 0), то система линейных уравнений общего вида (4.1) может быть приведена к нормальному виду. Для этого обе части матричного уравнения (4.3) надо умножить слева на транспонированную матрицу А = [ aji ]:

Пример 5. Рассмотрим следующую систему трех линейных уравнений:

Легко видеть, что для уравнений системы (4.52) выполнены условия (4.44), поэтому возможно решить данную систему итерационным методом. Используем метод Зейделя.

Приведем систему (4.52) к виду (4.35), необходимому для проведения итераций:

Так как выполнение условий (4.44) обеспечивает сходимость при любом начальном приближении, в качестве такового выберем нулевое:

( ( ( x10) =0; x20) =0; x30) =0. Подставим эти значения в правую часть первого уравнения системы (4.53) и легко получим первое приближение первого ( корня x11) =0,88889. При вычислении первого приближения второго ( ( корня x21) используем уже полученное значение x11) :

( ( ( x21) = 0,57142 + 0,28571 x11) + 0,14286 x30) = 0,82539.

Продолжим итерации методом Зейделя, а результаты запишем в таблицу 4.2.

В том, что точным решением системы (4.52) является x1 = x2 = x3 = 1, легко убедиться подстановкой полученных значений в исходную систему.

Таблица 4.Номер x1 x2 xитерации 0 0 0 1 0,88889 0,82539 1,2 0,95238 0,99773 1,3 0,99874 1,00061 0,4 1,00014 1,00003 0,5 1,00001 0,999999 0,6 1,000000 1,000000 1, Из таблицы 4.2 видно, что значения всех трех корней быстро сходятся к единице. Точность до шестого знака после запятой достигается на шестой итерации.

Глава 5. ВЫЧИСЛЕНИЕ ДЕТЕРМИНАНТОВ Каждая квадратная матрица A характеризуется определенным числом det A, которое называется детерминантом или определителем этой матрицы. Порядок детерминанта совпадает с порядком соответствующей матрицы.

Как следует из предыдущей главы, при решении системы линейных уравнений полезно (или даже необходимо) знать численное значение детерминанта матрицы коэффициентов при неизвестных. Значения детерминантов матриц требуются и в других прикладных задачах физики. Поэтому целесообразно в этой главе рассмотреть вопрос о вычислении детерминантов.

В линейной алгебре величина детерминанта определяется индуктивно. Квадратная матрица порядка n = 1 состоит из единственного элемента a11. Детерминант такой матрицы принимается равным этому элементу. Детерминант квадратной матрицы порядка n = 2 определяется следующей формулой:

В линейной алгебре доказана теорема, что детерминант n-го порядка может быть вычислен по следующей формуле:

n i+ j det A = (-1) aijMij, (5.2) j=где номер строки может принимать любое значение i = 1, …, n.

Формула (5.2) называется разложением детерминанта по минорам i-й строки. Справедлива и другая формула вычисления детерминанта n-го порядка разложением по минорам j-го столбца:

n i+ j det A = (-1) aijMij, (5.3) i=где номер j может быть выбран любым из множества: 1, …, n.

Таким образом, для вычисления одного детерминанта n-го порядка необходимо вычислить n детерминантов (n – 1)-го порядка. Для вычисления каждого минора можно вновь применить формулу (5.2). В результате, чтобы вычислить один детерминант n-го порядка этим методом приходится рассчитать n!/2 детерминантов 2-го порядка.

Кроме того, необходимо выполнить умножения миноров на коэффициенты aij исходной матрицы и провести суммирования по формулам (5.2) или (5.3). Ясно, что для высокого порядка вычисление детерминантов разложением по минорам является длительной операцией даже при использовании персональных компьютеров.

В линейной алгебре также используется метод выражения детерминантов непосредственно через коэффициенты матрицы aij без промежуточного вычисления миноров. Этот метод можно представить состоящим из следующих этапов.

После перебора всех перестановок индексов. все полученные произведения суммируются. Заметим, что количество перестановок равно n!.

Справедливость такого представления для детерминанта 2-го порядка видна непосредственно из формулы (5.1). Детерминант 3-го порядка, построенный последним методом, дает следующее выражение:

Пример 1. Необходимо вычислить детерминант следующей матрицы размера 44:

Иначе можно детерминанты 3-го порядка предварительно разложить и свести к вычислению нескольких детерминантов 2-го порядка. Если проводить разложение по минорам нижних строк, то (из-за того, что a= 0) для вычисления первого и третьего детерминантов в (5.6) потребуется вычислить только по два детерминанта 2-го порядка.

Описанный алгоритм может быть запрограммирован и реализован на персональном компьютере. Нетрудно подсчитать, что для вычисления детерминанта n-го порядка необходимо выполнить nn! умножений и n! сложений (или вычитаний). Следовательно, метод разложения по минорам практически не пригоден для вычисления детерминантов высоких порядков.

Более эффективный метод (требующий гораздо меньшего количества операций) базируется на следующей теореме линейной алгебры. Если к элементам любой строки (или любого столбца) детерминанта прибавить соответствующие элементы другой строки (или столбца), умноженные на произвольный множитель, то величина детерминанта не изменится. В частности, подобными операциями исходная квадратная матрица приводится к треугольному виду. Способ приведения квадратной матрицы к треугольному виду аналогичен процедуре прямого хода в методе Гаусса при решении системы линейных уравнений.

Процедура начинается с выбора ведущего элемента. Это может быть любой коэффициент ai1, не равный нулю. Переставляя строки (или столбцы) детерминанта, всегда можно ведущим элементом сделать коэффициент a11. При этом следует помнить, что при перестановке двух строк (или двух столбцов) знак детерминанта изменяется на противоположный.

Затем коэффициент a11 выносится из первого столбца в качестве общего множителя детерминанта. Вычитаем из элементов aij каждого jго столбца (j 2) соответствующие элементы ai1 первого столбца, умноженные на a1j. Преобразование элементов можно записать в виде:

det A = a11 n-1, (5.8) (1 (1 ( a22) a23). a21) n (1 (1 ( a32) a33). a31) n где n-1 = (5.9).

Следующий шаг заключается в применении к новому детерминанту n-1 той же процедуры. Выбирается новый ведущий элемент, не равный нулю. Переставляя при необходимости строки или столбцы нового (детерминанта, делаем ведущим элемент a22). Выносим его из первого столбца нового детерминанта в качестве общего множителя. Процедура продолжается, причем на каждом шаге данного алгоритма уменьшается порядок детерминанта. Преобразования элементов приводят к тому, что первая строка каждого нового детерминанта начинается с единицы.

Остальные элементы этой строки – нули.

В результате, если на каждом шаге удается найти ненулевой ведущий элемент, искомый детерминант n-го порядка представится в виде произведения этих ведущих элементов:

(1 (n det A = a11 a22). ann-1). (5.10) Этот способ вычисления детерминанта называется методом Гаусса.

Если на каком-либо шаге не удается отыскать ненулевой ведущий элемент, то это значит, что детерминант исходной матрицы равен нулю.

В терминологии матричной алгебры можно сказать, что проведенное преобразование исходной квадратной матрицы к треугольной позволяет выразить ее детерминант в виде произведения диагональных элементов полученной треугольной матрицы.

Можно подсчитать, что количество арифметических операций для вычисления детерминанта n-го порядка методом Гаусса не превышает n3. Следовательно, метод Гаусса предпочтительнее рассмотренных выше уже при n > 5.

Пример 2. Вычислим детерминант (5.5), приведенный в примере данной главы, но на этот раз используем метод Гаусса, изложенный выше.

Первый ведущий элемент a11 = 5. Преобразуем 2-ю строку данной матрицы по формуле (5.7):

j a(1 (1 (a22) =1–(–1)(–4)/5=1/5, a23) =1–(–1)0/5=1, a24) =–1 – (–1) 2/5=–3/5.

Аналогично преобразуются 3-я и 4-я строки данной матрицы:

j j j j (1 (a22) a22) Следующий детерминант получает вид:

(a33) 1 (1 (2 (Искомый детерминант равен det A = a11 a22) a33) a44) =5 (–20) = –6.

5 Конечно, детерминант 2 можно было бы сосчитать по формуле (5.1) (и представить результат в виде произведения det A = a11 a22) 2.

Искомое значение det A = –6 достигается еще быстрее.

Глава 6. ОБРАЩЕНИЕ МАТРИЦ Как известно из линейной алгебры, обратной матрицей A-1 по отношению к данной A называется матрица, которая будучи умноженной на A как справа, так и слева, дает единичную матрицу E:

E = [ ij ], (6.2) где 1 (i = j) ij = 0 (i j). (6.3) Матрицы, обратные данным, используются во многих прикладных задачах, в т.ч. и физических. Следовательно, существует потребность в методах, позволяющих вычислять элементы обратной матрицы, выражая их через элементы исходной.

В курсе линейной алгебры доказано, что обратная матрица A-существует, если исходная матрица A является неособенной, т.е. ее детерминант не равен нулю (det A 0). Методы вычисления детерминантов приведены в предыдущей главе.

Одна из теорем линейной алгебры утверждает, что обратная матрица A-1 может быть представлена как транспонированная матрица алгебраических дополнений исходной A, причем каждый элемент этой транспонированной матрицы должен быть поделен на детерминант det A. Алгебраическое дополнение Aij любого элемента матрицы aij выражается через его минор Mij:

Aij = (-1)i+j Mij. (6.4) Таким образом, обратная матрица A-1 выражается в следующем виде:

A11 A21. An A A22. An- A-1 =, (6.5).

1n A A1n. Ann где использовано обозначение = det A.

В принципе обратную матрицу можно вычислить по формуле (6.5).

За годы развития прикладной математики было разработано много различных способов обращения матриц: разбиение на клетки, окаймление, представление произведением треугольных матриц (LUфакторизация), схема Халецкого, и т.д. Эффективность некоторых методов повышается при специфическом виде обращаемой матрицы.

Для плохо обусловленных матриц, т.е. тех, у которых число обусловленности (4.32) много больше единицы, разработаны специальные методы обращения, обеспечивающие достаточную точность вычислений.

В эпоху распространения персональных компьютеров одним из широко используемых методов обращения хорошо обусловленных матриц является метод Гаусса.

n ik a xkj = ij (i, j = 1, …, n), (6.6) k =где ij – символ Кронекера (6.3).

Система (6.6) содержит n2 уравнений и является линейной относительно искомых неизвестных xij. Нетрудно заметить, что совокупность уравнений (6.6) состоит из n линейных систем, которые имеют одну и ту же матрицу коэффициентов при неизвестных (4.2).

Друг от друга системы уравнений отличаются векторами свободных членов ij, причем в каждой системе только один свободный член равен единице (остальные равны нулю). Каждой j-й набор свободных членов определяет j-й столбец xij (i = 1, …, n) искомой обратной матрицы A-1.

Поиск элементов xij обратной матрицы A-1 решением системы уравнений (6.6) эффективно осуществить алгоритмом Гаусса, который ранее успешно применялся в главах 4 и 5. Наличие нескольких столбцов свободных членов при неизменной матрице коэффициентов при неизвестных в системе уравнений (6.6) обусловливает некоторую специфику применения метода Гаусса к решению данной задачи обращения матрицы.

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Источник

Если на каком либо шаге не удается отыскать ненулевой ведущий элемент то это значит

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.

Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Решить систему (4.1) означает отыскать числа xi (i = 1, 2. n), которые при подстановке в (4.1) обращают все уравнения в тождества.

Набор этих чисел называется корнями системы (4.1).

Коэффициенты при неизвестных образуют квадратную матрицу A размером n n:

a11 a12. a1n a a22. a2n A =. (4.2).

na an2. ann Свободные члены и корни представляются столбцами или nмерными векторами b и x. Тогда систему (4.1) можно записать более кратко в матричном представлении:

A x = b (4.3) В линейной алгебре доказана следующая теорема: если детерминант (определитель) матрицы A не равен нулю, то система уравнений (4.1) имеет единственное решение. Т.е. при det A 0 существует только один набор чисел xi (i = 1, 2. n), который обращает в тождество систему (4.1). Следовательно, если мы ищем единственное решение системы уравнений (4.1), то прежде чем ее решать, необходимо убедиться, что детерминант матрицы коэффициентов при неизвестных не равен нулю.

Способам вычисления детерминантов посвящена глава 5.

Многочисленные способы решения системы линейных уравнений принято подразделять на две группы: прямые методы и итерационные.

Прямые методы позволяют найти решение с помощью определенного конечного количества операций. В итерационных методах решение ищется как предел последовательных приближений, где число итераций зависит от задаваемой погрешности корней. В §§4.1 – 4.4 рассмотрены простейшие прямые методы, итерационным методам посвящен §4.5.

Предположим, что условие det A 0 для системы (4.1) выполнено.

Тогда, согласно известной теореме матричной алгебры, для матрицы A существует обратная матрица A-1, для которой справедливы равенства:

Умножим слева обе части уравнения (4.3) на обратную матрицу A-1.

Принимая во внимание (4.4), получим:

Таким образом, умножение обратной матрицы A-1 на вектор (столбец) свободных членов b дает единственное решение: вектор корней x исходной системы (4.1). С точки зрения математики проблема решена.

Однако получение обратной матрицы в явном виде сопряжено с практическими трудностями. С ростом числа n требуемый объем вычислений резко возрастает. Заметим, что умножение матрицы на вектор представляет собой простую задачу, легко решаемую программным путем.

Задаче вычисления обратной матрицы посвящена глава 6. Далее в настоящей главе рассматриваются элементарные методы решения систем линейных уравнений, не требующие вычисления обратной матрицы.

§ 4.2. Метод Крамера Известно, что обратную матрицу можно представить в виде отношения:

Подставим (4.6) в уравнение (4.5) и умножим матрицу A* слева на столбец свободных членов b. В результате получим новый n-мерный вектор, компоненты которого i выражаются следующими суммами:

Можно доказать, что каждая величина i (i = 1, 2. n) равна детерминанту матрицы, которая получается из исходной A заменой i-го столбца на столбец свободных членов b:

a. an,i-1 bn an,i+1. ann n Для доказательства достаточно непосредственно вычислить детерминант матрицы (4.8) известным методом разложения по минорам i-го столбца, который описан в главе 5.

Следовательно, деление каждого числа i на детерминант матрицы (4.2) даст нам значение i-го корня исходной системы (4.1):

xi = i /, i =1, 2. n. (4.9) Описанная процедура вычисления корней системы линейных уравнений называется методом Крамера. В этом методе решение системы (4.1) полностью сводится к вычислению детерминантов, способы расчета которых подробно изложены в следующей главе.

Следует заметить, что в тех случаях, когда детерминант близок к нулю, метод Крамера может дать большую ошибку в значениях найденных корней, что непосредственно следует из формулы (4.9).

Конечно, погрешность вычисления корня существенно зависит и от величины соответствующего детерминанта i, стоящего в числителе формулы (4.9). Системы уравнений (4.1), у которых детерминант матрицы коэффициентов при неизвестных близок к нулю, требуют для своего решения специальных методов, которые не включены в настоящее учебное пособие.

Важнейшим недостатком алгоритма Крамера является большое количество необходимых арифметических операций. Из формул (4.9) ясно, что для решения данной системы (4.1) приходится вычислять (n+1) детерминантов, каждый порядка n. Рациональные методы расчета детерминантов рассматриваются в следующей главе. Пока заметим, что для вычисления детерминанта n-го порядка способом разложения по минорам требуется произвести n!(n – 1) умножений и примерно столько же делений. Следовательно, при решении системы линейных уравнений 40-го порядка методом Крамера придется выполнить 4140!39 умножений и сложений. Так как 40! 81047, то можно оценить, что при использовании самых быстродействующих компьютеров необходимое время решения во много раз превышает время существования нашей Вселенной. Кроме того, при выполнении процессором большого количества операций накапливается значительная погрешность результата, так как в каждой операции над реальными числами проводится округление.

При решении систем линейных уравнений для n = 2 и n = 3 метод Крамера легко реализуется и без использования компьютера. Для больших значений n целесообразно применять более эффективные методы.

§ 4.3. Метод Гаусса Метод Гаусса отличается сравнительно малым объемом вычислений и простотой алгоритма, что позволяет легко его программировать. Этот метод заключается, в сущности, в последовательном исключении неизвестных.

Процедура вычисления корней системы линейных уравнений состоит из двух частей: прямого хода и обратного хода.

Прямой ход состоит из отдельных шагов.

Очевидно, что все коэффициенты ai1 (i = 1. n) не могут равняться нулю. Равенство нулю всех ai1 (i = 1. n) означает наличие в матрице A нулевого столбца и равенство нулю детерминанта матрицы. В этом случае единственное решение системы отсутствует.

Уравнение с ведущим элементом делится на коэффициент a11 0 и приобретает вид:

n a1 j bx1 + x =. (4.10) a11 j aj=Теперь уравнение (4.10) умножается на коэффициент a21 и вычитается из 2-го уравнения исходной системы (4.1). Слагаемое, содержащее x1, исчезает из 2-го уравнения.

n (2), ij j a x = bi(2) i = 3. n. (4.14) j=В системе (4.14) введены новые обозначения:

(n ( ann-1) xn = bnn-1). (4.16) Таким образом, исходная система уравнений приведена к эквивалентной (т.е. имеющей те же корни), имеющей треугольную матрицу коэффициентов при неизвестных. При этом были преобразованы и свободные члены.

Заметим, что коэффициенты при неизвестных и свободные члены преобразовывались по идентичным рекуррентным формулам. Поэтому целесообразно предварительно построить расширенную матрицу размером n (n + 1), присоединив справа к квадратной матрице коэффициентов при неизвестных (n + 1)-й столбец свободных членов.

Тогда элементы расширенной матрицы сij ( i = 1. n, j = 1, …, (n + 1)) будут преобразовываться по рекуррентному закону:

После преобразования коэффициентов при неизвестных и свободных членов реализуется обратный ход.

На первом шаге обратного хода из уравнения (4.16) сразу вычисляется n-й корень системы (4.1):

Далее последовательно используются уравнения, полученные ранее на каждом шаге прямого хода. На предпоследнем шаге обратного хода вычисляется x2 с помощью уравнения (4.13). Значения корней xi (i = 3. n) уже получены в предыдущих шагах. На последнем (n-м) шаге вычисляется x1 с помощью уравнения (4.10).

Таким образом, исходная система линейных уравнений (4.1) полностью решена.

Примечание. В линейной алгебре доказано, что если det A 0, то на каждом шаге прямого хода найдется хотя бы один ведущий коэффициент, не равный нулю. Следовательно, можно специально не вычислять предварительно детерминант матрицы коэффициентов при неизвестных. Если на каком-либо шаге прямого хода не найдется ненулевой ведущий коэффициент, то это значит, что det A = 0 и система не имеет единственного решения.

Полезно сравнить количество вычислений, необходимых для решения системы линейных уравнений (4.1) методом Крамера и методом Гаусса, т.е. сравнить эффективности двух рассмотренных методов.

Если детерминанты вычислять методом разложения по минорам (см.

главу 5), то для расчета одного детерминанта n-го порядка приходится совершать количество операций умножения и деления, равное (n – 1) (n2+n+3) / 3. Это значит, что для решения системы из n линейных уравнений методом Крамера необходимо выполнить (n + 1) (n – 1) (n2 + n + 3) / 3 + n операций умножения и деления. Иначе говоря, число требуемых операций имеет порядок n4.

Можно вычислить, что при решении системы линейных уравнений n-го порядка методом Гаусса в прямом ходе выполняется n (n+1) (n+2) / 3 операций умножения и деления и столько же операций вычитания.

Таким образом, количество арифметических операций при решении системы линейных уравнений в методе Гаусса на порядок меньше, чем в методе Крамера. Это значит, что уже при n 4 целесообразно использовать метод Гаусса.

Проиллюстрируем метод Гаусса примером, причем для экономии места ограничимся системой из трех уравнений.

Пример 1. Дана следующая система уравнений:

Возьмем в качестве первого ведущего коэффициента a11 = 2.

Поделим на него первое уравнение. Затем исключим x1 из второго и третьего уравнений вычитанием преобразованного первого, домноженного на 2 и 3 соответственно. В результате первого шага прямого хода система принимает вид:

Затем исключается x2 из третьего уравнения сложением его с преобразованным вторым, умноженным на 4. Второй (и последний в данном примере) шаг прямого хода заканчивается получением треугольной матрицы коэффициентов при неизвестных:

Обратный ход начинается с вычисления x3 из последнего уравнения преобразованной системы: x3 = 3. Подставив полученное значение x3 во второе уравнение, получаем x2 = 2. Наконец, подстановка значений x3 и x2 в первое уравнение дает x1=1.

Подставив найденные значения корней в исходную систему, убеждаемся в правильности найденного решения.

§ 4.4. Уточнение корней и число обусловленности Погрешность, накапливающаяся при вычислениях, приводит к тому, что любой метод (Гаусса, Крамера и т.д.) дает не точное, а приближенное значение корней решаемой системы линейных уравнений.

Сначала рассмотрим случай, когда исходные данные: коэффициенты матрицы А и свободные члены имеют достаточную точность (например, все значащие цифры являются верными, а погрешность не превышает единицы младшего разряда). В этом случае необходимо оценить погрешность, которая накапливается в процессе выполнения алгоритма.

Для этого после решения системы следует полученные значения корней подставить в исходную систему (4.1) и вычислить левые части уравнений. Если они совпадут с соответствующими свободными членами (в пределах допустимых погрешностей), то решение можно полагать удовлетворительным. Если же наблюдается значимое расхождение, то необходимо применить более точный метод решения системы уравнений (4.1) или использовать процедуру уточнения корней.

Обозначим через x вектор точных значений корней, x(1) – вектор приближенных значений корней, полученных в ходе решения. Тогда точное решение можно представить в виде:

x = x(1) +, (4.20) где – вектор погрешностей. Каждая компонента вектора представляет собой разность между точным значением i-го корня и его приближенным значением i = xi – xi(1) (i = 1, …, n). (4.21) Подставляя (4.20) в исходную систему (4.3), получим новую систему линейных уравнений:

Полученные приближенные значения корней x(1) подставляются в (4.23) и вычисляются компоненты вектора невязок. Далее решается система уравнений (4.22), которая содержит исходную матрицу коэффициентов при неизвестных (4.2), а в качестве свободных членов используются вычисленные невязки (4.22). Решение системы проводится любым доступным способом, например тем же методом Гаусса. Результатом решения являются значения поправок (4.21) к приближенным значениям корней x(1). Суммы xi(1) + i (i = 1, …, n) (4.24) представляют собой уточненные значения корней исходной системы линейных уравнений (4.3).

Заметим, что при вычислении поправок также накапливается некоторая погрешность. Строго говоря, суммы (4.24) являются не точными решениями исходной системы (4.3), а вторым приближением.

Поэтому при необходимости процедуру уточнения корней можно повторить. Разумеется, в качестве оценки точности полученного решения используются относительные погрешности xi(1) /i.

Современные компьютеры обеспечивают высокую точность вычислений (т.е. малую погрешность округления арифметической операции), но при большом размере исходной системы линейных уравнений (4.1) рекомендуется провести процедуру уточнений корней.

Модификацией метода Гаусса, которая позволяет уменьшать накопление погрешностей в процессе решения, является так называемый метод главных элементов.

Как и в предыдущем параграфе, строится расширенная матрица из n строк и (n + 1) столбцов, т.е. к матрице коэффициентов при неизвестных присоединяется справа столбец свободных членов.

Источник