если проецирующие лучи перпендикулярны плоскости проекций то такое проецирование называется

Если проецирующие лучи перпендикулярны плоскости проекций то такое проецирование называется

Контрольные задания по теме: эпюр № 6

Для наглядного изображения предметов (изделий или их составных частей) рекомендуется применять аксонометрические проекции, выбирая в каждом отдельном случае наиболее подходящую из них.

Сущность метода аксонометрического проецирования заключается в том, что заданный предмет вместе с координатной системой, к которой он отнесен в пространстве, параллельным пучком лучей проецируется на некоторую плоскость. Направление проецирования на аксонометрическую плоскость не совпадает ни с одной из координатных осей и не параллельно ни одной из координатных плоскостей.

Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям. Под коэффициентом искажения понимается отношение величины изображения в аксонометрической проекции к величине изображения в ортогональной проекции.

В зависимости от соотношения коэффициентов искажения аксонометрические проекции подразделяются на:

— изометрические, когда все три коэффициента искажения одинаковы (k_x=k_y=k_z);

— диметрические, когда коэффициенты искажения одинаковы по двум осям, а третий не равен им (k_x= k_z ≠k_y);

— триметрические, когда все три коэффициенты искажения не равны между собой (k_x≠k_y≠k_z).

В зависимости от направления проецирующих лучей аксонометрические проекции подразделяются на прямоугольные и косоугольные. Если проецирующие лучи перпендикулярны аксонометрической плоскости проекций, то такая проекция называется прямоугольной. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая. Если проецирующие лучи направлены под углом к аксонометрической плоскости проекций, то такая проекция называется косоугольной. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

В прямоугольной изометрии углы между осями равны 120°. Действительный коэффициент искажения по аксонометрическим осям равен 0,82, но на практике для удобства построения показатель принимают равным 1. Вследствие этого аксонометрическое изображение получается увеличенным в 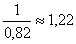раза.

Изометрические оси изображены на рисунке 57.

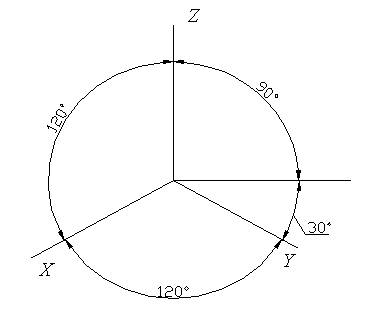
Рисунок 57

Рисунок 58

Построение изометрической проекции шестиугольника представлено на рисунке 59. Для этого необходимо отложить по оси X радиус описанной окружности шестиугольника в обе стороны относительно начала координат. Затем, по оси Y отложить величину размера под ключ, из полученных точек провести линии параллельно оси X и отложить по ним величину стороны шестиугольника.

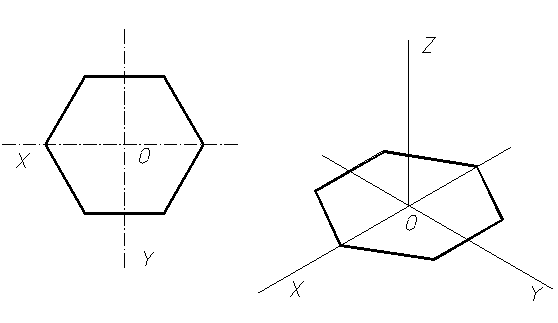
Рисунок 59

Построение окружности в прямоугольной изометрической проекции

Наиболее сложной плоской фигурой для вычерчивания в аксонометрии является окружность. Как известно, окружность в изометрии проецируется в эллипс, но построение эллипса довольно сложно, поэтому ГОСТ 2.317-69 рекомендует вместо эллипсов применять овалы. Существует несколько способов построения изометрических овалов. Рассмотрим один из наиболее распространенных.

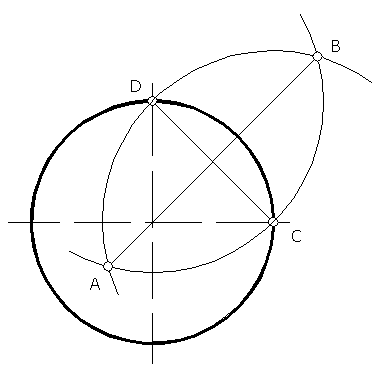
Рисунок 60

Установив направление большой и малой осей овала в зависимости от того, какой координатной плоскости принадлежит окружность, по размерам большой и малой оси проводят две концентрические окружности, в пересечении которых с осями намечают точки О₁, О₂, О₃, О₄, являющиеся центрами дуг овала (рисунок 61).

Для определения точек сопряжения проводят линии центров, соединяя О₁, О₂, О₃, О₄. из полученных центров О₁, О₂, О₃, О₄ проводят дуги радиусами R и R₁. размеры радиусов видны на чертеже.

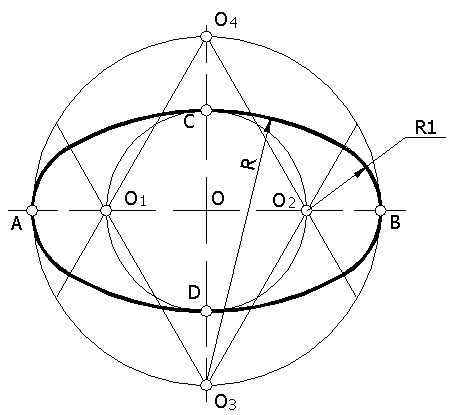
Рисунок 61

Направление осей эллипса или овала зависит от положения проецируемой окружности. Существует следующее правило: большая ось эллипса всегда перпендикулярна к той аксонометрической оси, которая на данную плоскость проецируется в точку, а малая ось совпадает с направлением этой оси (рисунок 62).

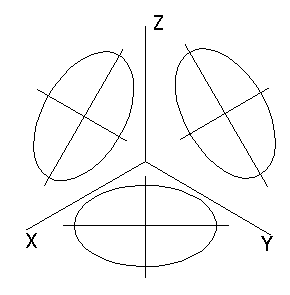
Рисунок 62

Штриховка и изометрической проекции

Линии штриховки сечений в изометрической проекции, согласно ГОСТ 2.317-69, должны иметь направление, параллельное или только большим диагоналям квадрата, или только малым.

Прямоугольной диметрией называется аксонометрическая проекция с равными показателями искажения по двум осям X и Z, а по оси Y показатель искажения в два раза меньше.

По ГОСТ 2.317-69 применяют в прямоугольной диметрии ось Z, расположенную вертикально, ось Х наклонную под углом 7°, а ось Y-под углом 41° к линии горизонта. Показатели искажения по осям X и Z равны 0,94, а по оси Y-0,47. Обычно применяют приведенные коэффициенты k_x=k_z=1, k_y=0,5, т.е. по осям X и Z или по направлениям им параллельным, откладывают действительные размеры, а по оси Y размеры уменьшают в два раза.

Для построения осей диметрии пользуются способом, указанным на рисунке 63, который заключается в следующем:

На горизонтальной прямой, проходящей через точку О, откладывают в обе стороны восемь равных произвольных отрезков. Из конечных точек этих отрезков вниз по вертикали откладывают слева один такой же отрезок, а справа – семь. Полученные точки соединяют с точкой О и получают направление аксонометрических осей X и Y в прямоугольной диметрии.

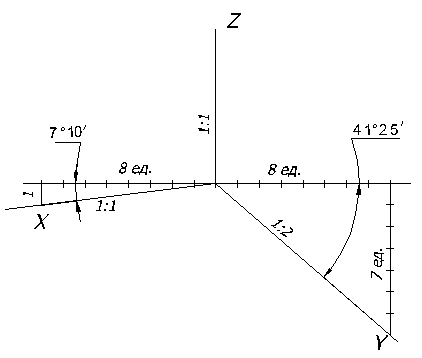
Рисунок 63

Построение диметрической проекции шестиугольника

Рассмотрим построение в диметрии правильного шестиугольника, расположенного в плоскости П₁ (рисунок 64).

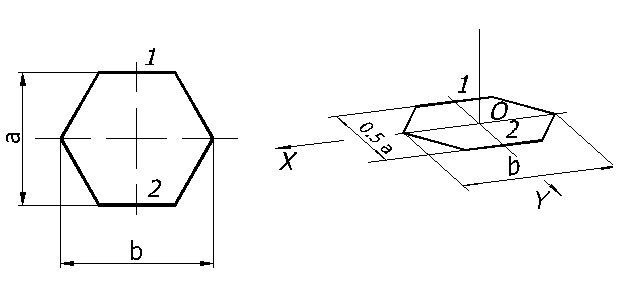
Рисунок 64

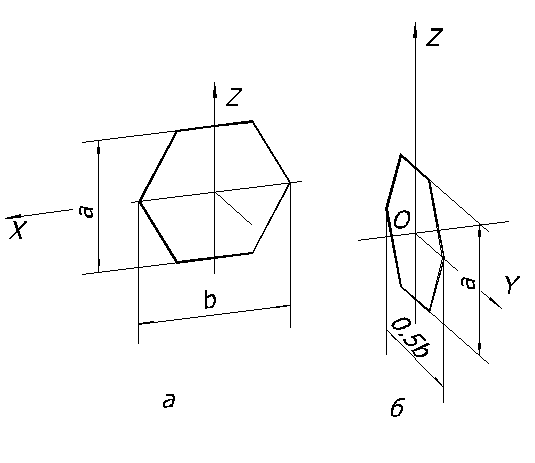
Рисунок 65

Построение окружности в диметрии

В прямоугольной диметрии все окружности изображаются эллипсами,

На практике эллипс заменяется четырехцентровым овалом. Рассмотрим построение овала, заменяющего проекцию окружности, лежащей в горизонтальной и профильной плоскостях (рисунок 66).

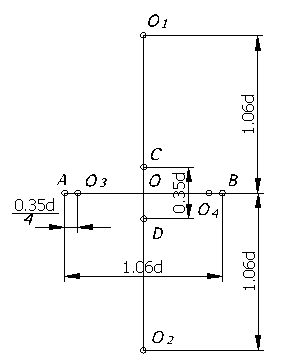
Рисунок 66

Затем, из точек О1 и О2 проводим дуги, радиус которых равен расстоянию до точек С и D, а из точек О3 и О4 – радиусом до точек А и В (рисунок 67).

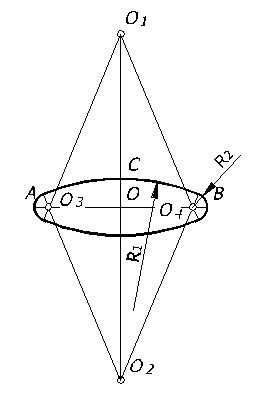
Рисунок 67

Построение овала, заменяющего эллипс, от окружности, расположенной в плоскости П₂, рассмотрим на рисунке 68. Проводим оси диметрии: Х, Y, Z. Малая ось эллипса совпадает с направлением оси Y, а большая перпендикулярна к ней. На осях Х и Z от начала откладываем величину радиуса окружности и получаем точки M, N, K, L, являющиеся точками сопряжения дуг овала. Из точек M и N проводим горизонтальные прямые, которые в пересечении с осью Y и перпендикуляром к ней дают точки О₁, О_2, О_3, О₄ – центры дуг овала (рисунок 68).

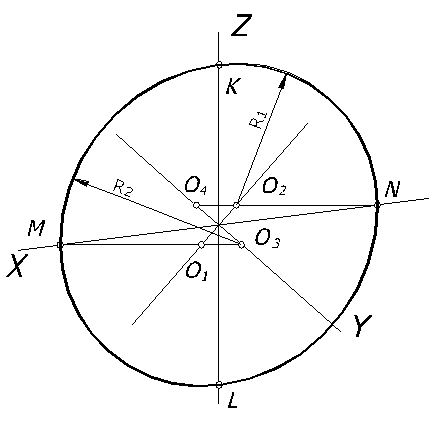
Рисунок 68

Штриховка а прямоугольной диметрии

Линии штриховки разрезов и сечений в аксонометрических проекциях выполняются параллельно одной из диагоналей квадрата, стороны которого расположены в соответствующих плоскостях параллельно аксонометрическим осям (рисунок 69).

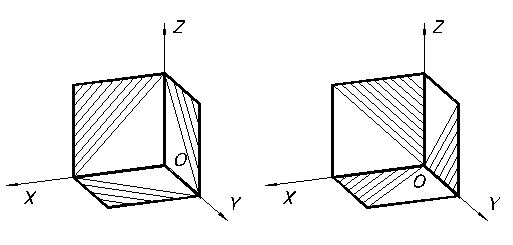
Рисунок 69

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Если проецирующие лучи перпендикулярны плоскости проекций то такое проецирование называется

Описанные построения выражают суть операции, называемой центральным проецированием точек пространства на плоскость.

В евклидовом пространстве существуют точки, которые не имеют центральных проекций, и наоборот в плоскости П_i есть точки, которые в пространстве не имеют оригиналов (точки D и F).

Точка D_i проекции прямой m_i не имеет оригинала на прямой m, так как проецирующий луч SD_i параллелен прямой.

Для исключения подобных случаев евклидово пространство расширяют введением несобственных (бесконечно удаленных) точек. Такое пространство называется расширенным евклидовым пространством.

Проецирующие лучи, проведенные через все точки кривой n , образуют проецирующую коническую поверхность N (рис.2). Проекция криволинейной фигуры, таким образом, представляет собой линию пересечения проецирующей поверхности N и плоскости проекций П _i .

Рисунок 2. Центральное проецирование линии

Рисунок 3. Центральное проецирование поверхности

Центральное проецирование есть наиболее общий случай проецирования геометрических объектов на плоскости.

Основными и неизменными его свойствами (инвариантами) являются следующие:

1) проекция точки – точка;

2) проекция прямой – прямая;

3) если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.

По принципу центрального проецирования работают фотоаппараты и кинокамеры. Упрощенная схема работы человеческого глаза близка к этому виду проецирования: роль центра проецирования выполняет оптический центр хрусталика, роль проецирующих прямых – лучи света; плоскостью проекций служит сетчатка глаза. Поэтому изображения, построенные по принципу центрального проецирования, наиболее наглядны и их широко используют в своей работе художники, архитекторы, дизайнеры и многие другие специалисты.

Частный случай центрального проецирования – параллельное проецирование , когда центр проецирования удален в бесконечность, при этом проецирующие лучи можно рассматривать как параллельные проецирующие прямые. Положение проецирующих прямых относительно плоскости проекций определяется направлением проецирования S (рис.4). В этом случае полученное изображение называют параллельной проекцией объекта.

При параллельном проецировании сохраняются свойства центрального и добавляются следующие:

проекции параллельных прямых параллельны между собой;

отношение отрезков прямой равно отношению их проекций;

отношение отрезков двух параллельных прямых равно отношению их проекций.

Рисунок 4. Параллельное проецирование

Прямоугольное (ортогональное) проецирование является частным случаем параллельного.

Проекция объекта, полученная с использование этого метода, называется ортогональной .

Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и кроме того, справедлива теорема о проецировании прямого угла: если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол .

К проекционным изображениям в начертательной геометрии предъявляются следующие основные требования:

1. Обратимость – восстановление оригинала по его проекционным изображениям (чертежу) – возможность определять форму и размеры объекта, его положение и связь с окружающей средой.

2. Наглядность – чертеж должен создавать пространственное представление о форме предмета.

3. Точность – графические операции, выполненные на чертеже, должны давать достаточно точные результаты.

4. Простота – изображение должно быть простым по построению и допускать однозначное описание объекта в виде последовательности графических операций.

Источник

Тема 5 «Проецирование» (для специальности «Дизайн» СПО)

Ищем педагогов в команду «Инфоурок»

Тема 5: «Проецирование»

5.1 Проекционное черчение

5.2 Аксонометрические проекции

5.3 Построение овала (аксонометрическая проекция окружности)

5.4 Построение разверток

5.5 Графическая работа №5 «Проецирование геометрических тел» (рекомендации по выполнению)

5.1 Проекционное черчение

Чтобы построить изображение предмета по методу проекций, необходимо через точки на предмете (например, через его вершины) провести воображаемые лучи до встречи их с плоскостью. Лучи, которые проецируют предмет на плоскость, называются проецирующими.

Рисунок 5.1- Центральное проецирование на плоскости

Рисунок 5.2- Перспектива

Также примерами центральной проекции являются кинокадры, тени, отброшенные от предмета лучами электрической лампочки, рисовании с натуры.

Рисунок 5.3 – Прямоугольное и косоугольное проецирование

Если проецирующие лучи составляют с плоскостью проекций прямой угол, то такие проекции называют прямоугольными.

Чертежи в системе прямоугольных проекций дают полное представление о форме и размерах предмета. Их легче выполнять, чем аксонометрические проекции (косоугольное проецирование).

Метод прямоугольного проецирования на две взаимно перпендикулярные плоскости был разработан французским ученым-геометром Гаспаром Монжем в конце XVIII века. Поэтому такой метод иногда называют методом Монжа. Г. Монж положил начало развитию новой науки об изображении предметов – начертательной геометрии.

Правила изображения предметов, а также расположения этих изображений на чертежах для всех отраслей промышленности и строительства устанавливает ГОСТ 2.305-68*. Изображения предметов должны выполняться по методу прямоугольного проецирования. Изображаемый предмет считается расположенным между наблюдателем и соответствующей плоскостью проекций.

Что нужно знать для успешного выполнения чертежей?

Всякий предмет, имеющий плоские поверхности, ограничивается вершинами, ребрами и гранями (рис. 5.4). Следовательно, чтобы научиться изображать на чертежах разнообразные предметы, нужно знать, как в прямоугольных проекциях изображаются вершины (точки), ребра (отрезки прямых линий) и грани предметов (части плоскости).

Рисунок 5.4 – Предмет как совокупность точек, ребер, граней

За основные плоскости проекций принимают шесть граней куба, на которые может быть спроецирован любой предмет (рис. 5.5).

Рисунок 5.5 – Плоскости проекций

Рассмотрим проецирование точки А на три взаимно перпендикулярные плоскости.

Вторую плоскость проекций ( V) располагают вертикально. Вертикальных плоскостей может быть несколько, поэтому плоскость проекций, расположенную перед зрителем, называют фронтальной (от французского слова «фронталь», что означает «лицом к зрителю»). Полученную на эту плоскость проекцию предмета называют фронтальной.

Рисунок 5.6 – Прямоугольное проецирование точки А

Линии пересечения плоскостей являются осями проекций ox, оу, oz (рис. 7). Обратим внимание на то, что проекции а’ и а, а’ и а» , а и а» лежат на прямых, называемых линиями проекционной связи. Такая зависимость в расположении проекции точки называется проекционной связью и при выполнении чертежей должна обязательно соблюдаться. Чертеж, состоящий из нескольких прямоугольных проекций, называется чертежом в системе прямоугольных проекций, или ортогональным чертежом.

Рассмотрим примеры расположения отрезков и плоских изображений к основным плоскостям проекций (рис.5.8):

Рисунок 5.8 – Проецирование плоской фигуры на три плоскости проекции

Рисунок 5.9 – Проецирование объемного тела на одну плоскость проекции

5.2 Аксонометрические проекции

Аксонометрические проекции представляют собой наглядное и достаточно точное изображение предметов. Слово «аксонометрия» — греческое. Оно состоит из двух слов: ахсоп — ось и metreo — измерение, что означает измерение по осям (или измерение параллельно осям).

Аксонометрические проекции любого предмета начинают строить с осей. Различные способы построения осей фронтальной диметрической и изометрической проекций показаны на рис. 5.10.

Рисунок 5.10 – Построение осей

Рисунок 5.11 – Виды аксонометрических проекций (положение осей)

Рисунок 5.12 – Построение аксонометрической проекции куба

Задание для самостоятельной работы:

Задание 5.1: Выполнить построение плоских фигур, лежащих в горизонтальной плоскости проекций по таблице 5.1. Доработать чертежи, из оснований построить четырехугольную и шестиугольную пирамиды, треугольную призму. Примеры построения геометрических тел представлены на рисунках 5.13-5.15.

Таблица 5.1 – Построение аксонометрических проекций плоских фигур

Рисунок 5.13 – Комплексный чертеж четырехугольной пирамиды

Рисунок 5.14 – Комплексный чертеж треугольной призмы

Рисунок 5.15 – Комплексный чертеж цилиндра и конуса

Комплексным чертежом называют изображения предмета, составленные из двух или более связанных между собой ортогональных проекций изображаемого геометрического образа (рис. 5.16).

Так строят чертежи в прямоугольных проекциях. Используя размеры детали и перенося их с имеющихся видов на достраиваемый, можно построить чертеж детали любой сложности.

Задание для самостоятельной работы:

Задание 5.2: Построить фронтальную диметрическую проекцию детали по рисунку 5.17 и изометрическую проекцию самостоятельно.

Рисунок 5.17 – Построение аксонометрической проекции

по комплексному чертежу

Примеры построения проекций ребер, граней, образующих форму геометрических тел показаны на рисунке 5.18.

Рисунок 5.18 – Проецирование ребер, граней, образующих форму геометрических тел

Рисунок 5.19 – Схема построения аксонометрической проекции точки по ее координатам

Задания для самостоятельной работы:

Задание 5.3: Построить изометрическую проекцию детали и проекцию точки а по комплексному чертежу, представленному на рисунке 5.20. Параметры детали ( b =10; h =35; l =40; D =30). Проекцию точки а выполнять по схеме, представленной на рисунке 5.19. Построение овала см. в разделе 5.3.

Рисунок 5.20 – Комплексный чертеж детали

Задание 5.4: Выполнить по образцу рис.5.21 чертежи геометрических тел, найти проекции точек м и к (координаты см. на рисунке).

Рисунок 5.21 – Задание для самостоятельной работы

5.3 Построение овала (аксонометрическая проекция окружности)

Рисунок 5.22 – Примеры построения овала

5.4 Построение разверток

Построение разверток поверхностей имеет большое практическое значение, так как яв­ляется важнейшим технологическим этапом в тех ви­дах производства, которые связаны с листовыми материалами.

Без растяжения и сжатия можно совместить с плоскостью, не получив ни складок, ни разрывов, поверхности только нескольких видов геометриче­ских тел: многогранников (в том числе призм и пи­рамид), цилиндров и конусов. Такие развертки называют точными.

Для всех других поверхностей (сфера, тор и др.) строят условные развертки. Их точность не столь вы­сока; здесь возможно использование растяжения или сжатия (механическим, температурно-влажностным и др. воздействием).

Развертка — плоская фигура, полученная совмещением поверхностей геометрического тела с плоскостью. Все многогранные поверхности относятся к развертываемым. Их можно сов­местить с плоскостью без образования складок и разрывов. Кривые поверхности не развертываются. Их раз­вертки строят приближенно, заменяя кривую поверхность много­гранной, цилиндрической или конической. К развертываемым от­носятся лишь некоторые линейчатые, например цилиндр и конус.

Линии сгиба на развертке изображают штрихпунктирной линией с двумя точками, контур развертки обводят сплошной толстой основной линией. Над изображением наносят специальный знак. От линий сгиба проводят ли­нии-выноски и пишут на полке: «Линии сгиба».

Рисунок 5.23 – Чертежи разверток поверхностей геометрических тел

Для выполнения упаковки в форме куба и пирамиды, необходимо выполнить чертежи разверток правильных выпуклых многогранников: куба (гексаэдра), тетраэдра (четырехгранника) и октаэдра (восьмигранника), и т.д.

Рисунок 5.24 – Примеры разверток упаковок

5.5 Графическая работа №5 «Проецирование геометрических тел» (рекомендации по выполнению)

Целью данной работы является приобретение навыков вычерчивания комплексных чертежей, построения аксонометрических проекций и разверток поверхностей геометрических тел.

Пример оформления Графической работы №5 представлен на рисунке 5.26.

Работа выполняется на чертежной бумаге формата А3 (297×420 мм). Размещение листа может быть альбомным или книжным (по усмотрению студента, выполняющего работу).

Рекомендации по выполнению работы:

Задание: Выполнить графическую работу в соответствии с образцом. Образец выполнения работы представлен на рисунке 5.25. Варианты параметров для выполнения задания представлены в приложении А данного пособия.

Рисунок 5.25 – Образец выполнения Графической работы №5

Рисунок 5.26 – Пример оформления Графической работы №5

Вопросы для самоконтроля:

Что такое проецирование? Назовите виды проецирования.

Какое проецирование называется ортогональным?

Дайте названия плоскостям проекций, что они означают?

В каком случае отрезок проецируется в точку?

В каком случае отрезок проецируется в натуральную величину?

Что означает понятие «аксонометрия»?

Какие виды аксонометрических проекций бывают?

Как иначе называется аксонометрическая проекция окружности?

Что такое «развертка»?

Какой линией обозначаются сгибы на развертках?

Источник