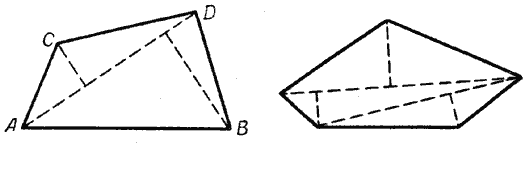
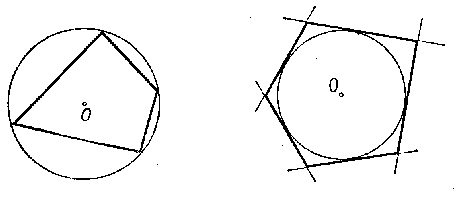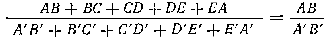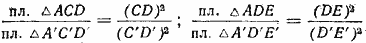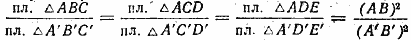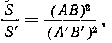если у двух многоугольников равны все их соответственные стороны то такие многоугольники равны

Математика

Подобные многоугольники. Подобными называются такие одноименные многоугольники, у которых соответственные углы равны и соответственные стороны пропорциональны.

Соответственными сторонами подобных многоугольников называются стороны, соединяющие равные углы.

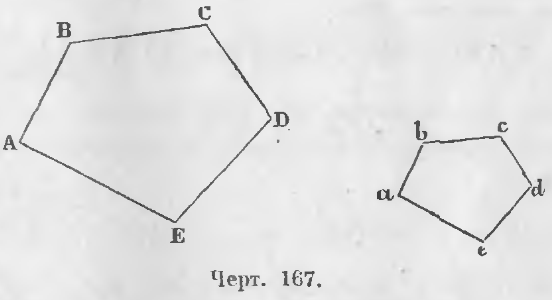
Два многоугольника ABCDE и abcde (черт. 167) подобны, если

∠A = ∠a, ∠B = ∠b, ∠C = ∠c, ∠D = ∠d, ∠E = ∠e и
AB/ab = BC/bc = CD/cd = DE/de = EA/ea

Отношение подобия. Отношение двух соответствующих сторон называется отношением подобия.

Теорема 108. Периметры подобных многоугольников относятся как соответственные стороны.

Дано. Обозначим периметры двух подобных многоугольников (черт. 167) через P и p.

P = AB + BC + CD + DE + EA
p = ab + bc + cd + de + ea

Требуется доказать, что P/p = AB/ab.

Доказательство. Из самого определения подобия двух многоугольников ABCDE и abcde (черт. 167) вытекают равенства:

AB/ab = BC/bc = CD/cd = DE/de = EA/ea

На основании той теоремы, что сумма предыдущих относится к сумме последующих как предыдущий член относится к последующему, имеет место равенство:

(AB + BC + CD + DE + EA) / (ab + bc + cd + de + ca) = AB/ab

откуда P/p = AB/ab (ЧТД).

Теорема 109. Подобные многоугольники разбиваются диагоналями на треугольники подобные и одинаково расположенные.

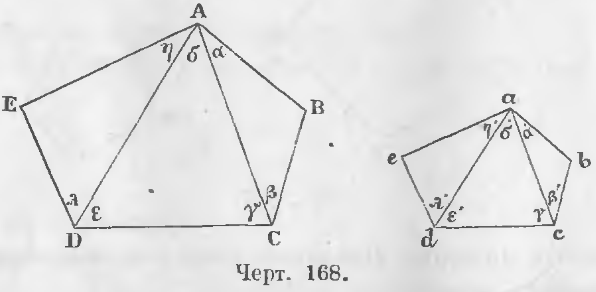
Дано. Разобьем подобные многоугольники ABCDE и abcde диагоналями AC, AD, ac, ad на одинаково расположенные треугольники (черт. 168).

Требуется доказать, что

Доказательство. Из подобия многоугольников следует, что углы равны и стороны пропорциональны.

∠A = ∠a, ∠B = ∠b, ∠C = ∠c, ∠D = ∠d, ∠E = ∠e и
AB/ab = BC/bc = CD/cd = DE/de = EA/ea

1) Треугольники ABC и abc подобны, ибо

2) Точно также треугольники ACD и acd подобны, ибо

∠ γ = ∠ γ’ и
AC/ac = CD/cd

3) Наконец треугольники ADE и ade подобны, ибо

Из этой теоремы вытекает следствие. В подобных многоугольниках стороны пропорциональны диагоналям.

Теорема 110 (обратная 109). Два многоугольника, состоящие из одинаково расположенных подобных треугольников, подобны.

Требуется доказать, что многоугольники ABCDE и abcde подобны.

Доказательство. Из подобия треугольников ABC и abc следует, что углы

B = b, α = α’, β = β’ и
AB/ab = BC/bc = AC/ac (1)

Из подобия треугольников ACD и acd следует, что углы

γ = γ’, δ = δ’ и
AC/ac = CD/cd = AD/ad (2)

Из подобия треугольников ADE и ade следует, что

η = η’, λ = λ’, E = e и
AD/ad = AE/ae = DE/de (3)

Из равенства для углов выходит, что

B = b
A = α + δ + η = α’ + δ’ + η’ = a
E = e
D = ε + λ = ε’ + λ’ = d
C = β + γ = β’ + γ’ = c

Из сравнения равенств (1), (2) и (3) вытекает, что

AB/ab = BC/bc = CD/cd = DE/de = AE/ae

следовательно многоугольники ABCDE и abcde подобны (ЧТД).

Источник

ВОПРОСЫ

1. Какая фигура ограничивает многоугольник?

Многоугольник ограничивает замкнутая ломаная.

2. Могут ли звенья ломаной, ограничивающей многоугольник, пересекаться?

Звенья ломаной, ограничивающей многоугольник, пересекаться не могут.

3. Какие элементы многоугольника вы знаете?

Элементы многоугольника: стороны, углы, вершины.

4. Как называют и обозначают многоугольник?

5. Что называют периметром многоугольника?

Сумму длин всех сторон многоугольника называют его периметром.

6. Какие многоугольники называют равными?

Два многоугольника называют равными, если они совпадают при наложении.

7. Какие фигуры называют равными?

Две фигуры называют равными, если они совпадают при наложении.

РЕШАЕМ УСТНО

1. Сумму чисел 24 и 18 уменьшите на 33.

2. Разность чисел 30 и 14 увеличьте в 3 раза.

3. Произведение чисел 12 и 5 увеличьте на 19.

4. Частное чисел 189 и 9 уменьшите в 7 раз.

5. Укажите среди данных отрезков равные, если: АВ = 5 см 3 мм, CD = 4 м 5 см, PK = 45 см, EF = 2 дм 8 мм, TQ = 53 мм, MN = 208 мм.

УПРАЖНЕНИЕ

321. Назовите вершины и стороны пятиугольника, изображённого на рисунке 109.

322. Начертите: 1) четырёхугольник; 2) пятиугольник; 3) шестиугольник; 4) семиугольник.

323. Вычислите периметр пятиугольника, стороны которого равны 2 см, 4 см, 5 см 5 мм, 6 см, 7 см.

325. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 110.

326. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 111.

328. Стороны пятиугольника пронумеровали. Первая сторона равна 4 см, а каждая следующая сторона на 2 см длиннее предыдущей. Вычислите периметр пятиугольника.

330. Как, используя шаблон угла, градусная мера которого 130, построить угол, градусная мера которого равна 20?

331. Как построить угол, градусная мера которого 10, используя шаблон угла, градусная мера которого равна: а) 190; б) 70?

332. Существует ли многоугольник с периметром, равным 1 000 000 см, который можно целиком расположить в квадрате со стороной 1 см?

УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ

333. Сравните:

334. Выполните сложение, выбирая удобный порядок вычислений:

ЗАДАЧА ОТ МУДРОЙ СОВЫ

337. Лимоны одинаковой массы продают поштучно. Масса каждого лимона составляет целое количество граммов. Купили больше двух, но меньше семи лимонов. Масса всей покупки составляет 850 г. Какова масса одного лимона?

Источник

Понятие площади многоугольника (окончание)

Вывод этих формул основан на свойствах площадей, которые мы сейчас рассмотрим.

Прежде всего отметим, что если два многоугольника равны, то единица измерения площадей и её части укладываются в таких многоугольниках одинаковое число раз, т. е. имеет место следующее свойство:

Далее, пусть многоугольник составлен из нескольких многоугольников так, что внутренние области любых двух из этих многоугольников не имеют общих точек, как показано на рисунке 178. Очевидно, величина части плоскости, занимаемой всем многоугольником, является суммой величин тех частей плоскости, которые занимают составляющие его многоугольники. Итак:

Свойства 1 0 и 2 0 называют основными свойствами площадей. Напомним, что аналогичными свойствами обладают длины отрезков.

Наряду с этими свойствами нам понадобится ещё одно свойство площадей.

Если площади двух многоугольников равны, то эти многоугольники называются равновеликими. Если один многоугольник разрезан на несколько многоугольников и из них составлен другой многоугольник, то такие многоугольники называются равносоставленными. Например, прямоугольник со сторонами, равными 2 см и Зсм (см. рис. 177, а), равносоставлен с прямоугольником со сторонами, равными 1 см и 6 см. Ясно, что любые два равносоставленных многоугольника равновеликие (см. основные свойства площадей). Оказывается, что верно и обратное утверждение: если два многоугольника равновеликие, то они равносоставленные. Это утверждение называется теоремой Бойяи — Гервина. Венгерский математик Ф. Бойяи доказал эту теорему в 1832 г., а немецкий математик-любитель П. Гервин независимо от Ф. Бойяи доказал её в 1833 г.

Источник

Многоугольники

Часть плоскости, ограниченная замкнутой ломаной линией, называется многоугольником.

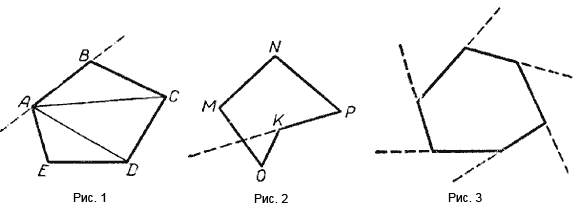
Отрезки этой ломаной линии называются сторонами многоугольника. АВ, ВС, CD, DE, ЕА (рис. 1) — стороны многоугольника ABCDE. Сумма всех сторон многоугольника называется его периметром.

Многоугольник называется выпуклым, если он расположен по одну сторону от любой своей стороны, неограниченно продолженной за обе вершины.

Многоугольник MNPKO (рис. 1) не будет выпуклым, так как он расположен не по одну сторону прямой КР.

Мы будем рассматривать только выпуклые многоугольники.

Углы, составленные двумя соседними сторонами многоугольника, называются его внутренними углами, а вершины их — вершинами многоугольника.

Отрезок прямой, соединяющий две несоседние вершины многоугольника, называется диагональю многоугольника.

АС, AD — диагонали многоугольника (рис. 2).

Углы, смежные с внутренними углами многоугольника, называются внешними углами многоугольника (рис. 3).

В зависимости от числа углов (сторон) многоугольник называется треугольником, четырёхугольником, пятиугольником и т. д.

Два многоугольника называются равными, если их можно совместить наложением.

Вписанные и описанные многоугольники

Если все вершины многоугольника лежат на окружности, то многоугольник называется вписанным в окружность, а окружность — описанной около многоугольника (рис).

Если все стороны многоугольника являются касательными к окружности, то многоугольник называется описанным около окружности, а окружность называется вписанной в многоугольник (рис).

Подобие многоугольников

Два одноимённых многоугольника называются подобными, если углы одного из них соответственно равны углам другого, а сходственные стороны многоугольников пропорциональны.

Одноимёнными называются многоугольники, имеющие одинаковое число сторон (углов).

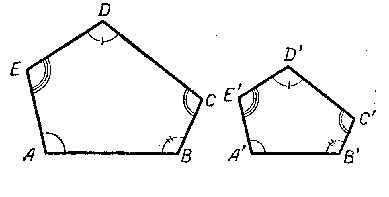
Сходственными называются стороны подобных многоугольников, соединяющие вершины соответственно равных углов (рис).

Так, например, чтобы многоугольник ABCDE был подобен многоугольнику A’B’C’D’E’, необходимо, чтобы: ∠A = ∠A’ ∠B = ∠B’ ∠С = ∠С’ ∠D = ∠D’ ∠Е = ∠Е’ и, кроме того, AB /_A’B’ = BC /_B’C’ = CD /_C’D’ = DE /_D’E’ = EA /_E’A’.

Отношение периметров подобных многоугольников

Сначала рассмотрим свойство ряда равных отношений. Пусть имеем, например, отношения: 2 /₁ = 4 /₂ = 6 /₃ = 8 /₄ =2.

Найдем сумму предыдущих членов этих отношений, затем — сумму их последующих членов и найдём отношение полученных сумм, получим:

То же самое мы получим, если возьмём ряд каких-нибудь других отношений, например: 2 /₃ = 4 /₆ = 6 /₉ = 8 /₁₂ = 10 /₁₅= 2 /₃ Найдем сумму предыдущих членов этих отношений и сумму последующих, а затем найдём отношение этих сумм, получим:

В том и другом случае сумма предыдущих членов ряда равных отношений относится к сумме последующих членов этого же ряда, как предыдущий член любого из этих отношений относится к своему последующему.

Мы вывели это свойство, рассмотрев ряд числовых примеров. Оно может быть выведено строго и в общем виде.

Теперь рассмотрим отношение периметров подобных многоугольников.

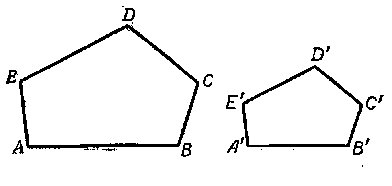
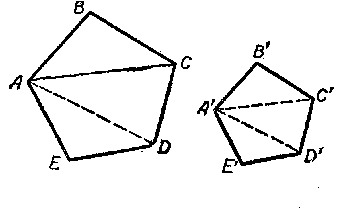
Пусть многоугольник ABCDE подобен многоугольнику A’B’C’D’E’ (рис).

Из подобия этих многоугольников следует, что

На основании выведенного нами свойства ряда равных отношений можем написать:

Следовательно, периметры подобных многоугольников относятся как их сходственные стороны.

Отношение площадей подобных многоугольников

Пусть ABCDE и A’B’C’D’E’ — подобные многоугольники (рис).

;

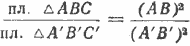
Так как вторые отношения этих пропорций равны, что вытекает из подобия многоугольников, то

Используя свойство ряда равных отношений получим:

, или

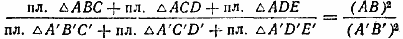
где S и S’ — площади данных подобных многоугольников.

Следовательно, площади подобных многоугольников относятся как квадраты сходственных сторон.

Полученную формулу можно преобразовать к такому виду: S /_S’ = ( AВ /_A’В’ ) 2

Площадь произвольного многоугольника

Пусть требуется вычислить площадь произвольного четырёхугольника АВDС (рис).

Проведём в нём диагональ, например АD. Получим два треугольника АВD и АСD, площади которых вычислять умеем. Затем находим сумму площадей этих треугольников. Полученная сумма и будет выражать площадь данного четырёхугольника.

Если нужно вычислить площадь пятиугольника, то поступаем таким же образом: из одной какой-нибудь вершины проводим диагонали. Получим три треугольника, площади которых можем вычислить. Значит, можем найти и площадь данного пятиугольника. Так же поступаем при вычислении площади любого многоугольника.

Площадь проекции многоугольника

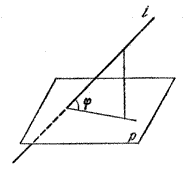
Напомним, что углом между прямой и плоскостью называется угол между данной прямой и ее проекцией на плоскость (рис.).

Теорема. Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла, образованного плоскостью многоугольника и плоскостью проекции.

Каждый многоугольник можно разбить на треугольники, сумма площадей которых равна площади многоугольника. Поэтому теорему достаточно доказать для треугольника.

Пусть ΔАВС проектируется на плоскость р. Рассмотрим два случая:

а) одна из сторон ΔАВС параллельна плоскости р;

б) ни одна из сторон ΔАВС не параллельна р.

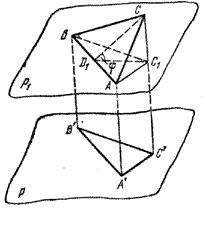
Рассмотрим первый случай: пусть [АВ] || р.

По свойству проекции имеем ΔАВС₁ (cong) ΔА’В’С’, и поэтому

Проведем [CD₁] ⊥ [AB] и отрезок D₁C₁. Тогда [D₁C₁] ⊥ [AB], a \( \overbrace\) = φ есть величина угла между плоскостью ΔАВС и плоскостью р₁. Поэтому

и, следовательно, S_{Δ A’B’C’} = S_{Δ ABC} cos φ.

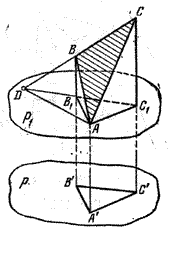
Перейдем к рассмотрению второго случая. Проведем плоскость р₁ || р через ту вершину ΔАВС, расстояние от которой до плоскости р наименьшее (пусть это будет вершина А).

Спроектируем ΔАВС на плоскости р₁ и р (рис.); пусть его проекциями будут соответственно ΔАВ₁С₁ и ΔА’В’С’.

S_{Δ A’B’C’} = S_{ΔAB 1 C 1} = S_{ΔADC 1} — S_{ΔADB 1} = ( S_ΔADC — S_ΔADB) cos φ = S_{Δ ABC} cos φ

Источник

Многоугольники. Равные фигуры

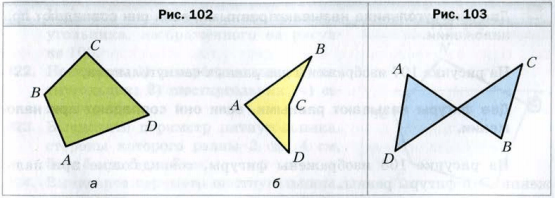
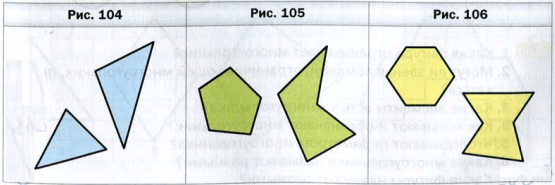
На рисунках 102 и 103 изображены три фигуры, каждая из которых ограничена замкнутой ломаной, состоящей из четырех звеньев AB, BC, CD, DA.

Фигуры, изображенные на рисунке 102, называют четырехугольниками.

На рисунке 104 изображены треугольники, на рисунке 105 − пятиугольники, на рисунке 106 − шестиугольники.

Все эти фигуры являются примерами многоугольников. Фигура, изображенная на рисунке 103, многоугольником не является.

Каждый многоугольник имеет вершины и стороны. Так, на рисунке 102, a точки A, B, C, D − вершины четырехугольника, отрезки AB, BC, CD, DA − его стороны, а углы A, B, C, D − углы четырехугольника.

Многоугольник называют и обозначают по его вершинам. Для этого надо последовательно записать или назвать все его вершины, начиная с любой.

Изображенные на рисунке 102 четырехугольники можно назвать, например, так : ABCD, или BCDA, или DCBA и т.п.

Сумму длин всех сторон многоугольника называют его периметром.

Два многоугольника называют равными, если они совпадают при наложении.

На рисунке 107 изображены два равных семиугольника.

Две фигуры называют равными, если они совпадают при наложении.

На рисункее 108 изображены фигуры, совпадающие при наложении. Эти фигуры равны.

Источник