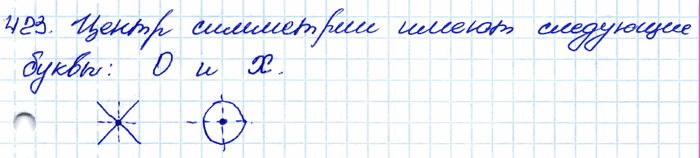если в четырехугольнике две диагонали равны и перпендикулярны то такой четырехугольник квадрат
Если в четырехугольнике две диагонали равны и перпендикулярны то такой четырехугольник квадрат
Укажите номер верного утверждения.
1) Если в параллелограмме две стороны равны, то такой параллелограмм является ромбом.
2) Если в четырёхугольнике две диагонали равны и перпендикулярны, то такой четырёхугольник — квадрат.
3) Если в ромбе диагонали равны, то такой ромб является квадратом.
4) Углы при меньшем основании трапеции тупые.
Проверим каждое из утверждений.
1) «Если в параллелограмме две стороны равны, то такой параллелограмм является ромбом» — неверно, поскольку у любого параллелограмма противоположные стороны равны, однако он не обязан быть ромбом. Правильно утверждение: параллелограмм является ромбом, только если смежные стороны равны.
2) «Если в четырёхугольнике две диагонали равны и перпендикулярны, то такой четырёхугольник — квадрат» — неверно, поскольку существуют четырёхугольники с равными взаимно перпендикулярными диагоналями, но не являющиеся квадратами. Правильное утверждение: Если в четырёхугольнике две диагонали равны и перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник — квадрат.
3) «Если в ромбе диагонали равны, то такой ромб является квадратом» — верно.
4) «Углы при меньшем основании трапеции тупые» — неверно, например, у прямоугольной трапеции только один угол при меньшем основании тупой.
Геометрия 8 класс Атанасян Задачи 399-423
Упражнения 399 — 423 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат (46. Прямоугольник. 47. Ромб и квадрат. 48. Осевая и центральная симметрии). Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия 8 класс Атанасян
Глава 5. § 3. Прямоугольник, ромб, квадрат
Задачи №№ 399 — 423:
Задача № 399. □ Докажите, что параллелограмм, один из углов которого прямой, является прямоугольником.
Задача № 400. □ Докажите, что если в четырёхугольнике все углы прямые, то четырёхугольник — прямоугольник.
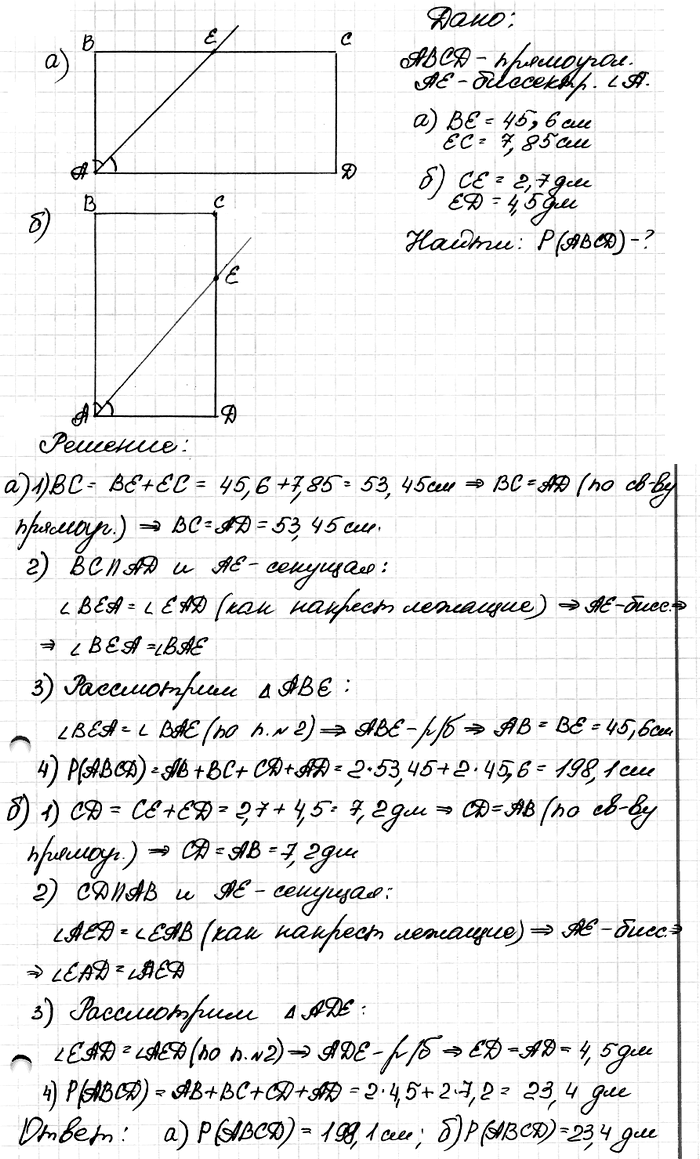
Задача № 401. Найдите периметр прямоугольника ABCD, если биссектриса угла А делит сторону: а) ВС на отрезки 45,6 см и 7,85 см; б) DC на отрезки 2,7 дм и 4,5 дм.
Задача № 402. □ Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что треугольники AOD и АОВ равнобедренные.
Задача № 403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если ∠CAD = 30°, АС = 12 см.
Задача № 404. □ Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
Задача № 405. □ В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы, которые диагонали ромба образуют с его сторонами.
Задача № 406. Найдите периметр ромба ABCD, в котором ∠B = 60°, АС= 10,5 см.
Задача № 407. Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 45°.
Задача № 408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ делит его угол пополам.
Задача № 409. □ Докажите, что ромб, у которого один угол прямой, является квадратом.
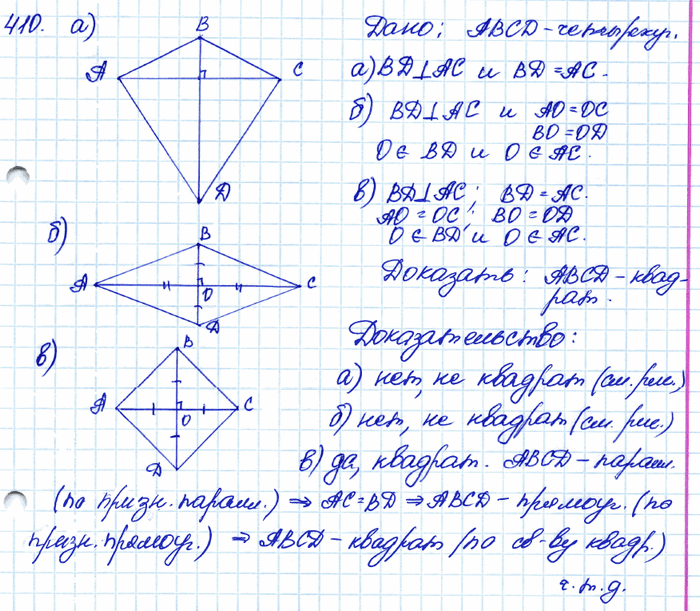
Задача № 410. □ Является ли четырёхугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину?
Задача № 411. □ В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырёхугольник — квадрат.
Задача № 412. Даны равнобедренный прямоугольный треугольник АВС с прямым углом С, катетом АС = 12см и квадрат CDEF, такой, что две его стороны лежат на катетах, а вершина Е — на гипотенузе треугольника. Найдите периметр квадрата.
Задача № 413. □ Постройте прямоугольник: а) по двум смежным сторонам; б) по стороне и диагонали; в) по диагонали и углу между диагоналями.
Задача № 414. □ Постройте ромб: а) по двум диагоналям; б) по стороне и углу.
Задача № 415. □ Постройте квадрат: а) по стороне; б) по диагонали.
Задача № 416. □ Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой.
Задача № 417. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?
Задача № 419. □ Докажите, что прямая, проходящая через середины противоположных сторон прямоугольника, является его осью симметрии.
Задача № 420. □ Докажите, что прямая, содержащая биссектрису равнобедренного треугольника, проведённую к основанию, является осью симметрии треугольника.
Задача № 421. □ Даны точки А, В и М. Постройте точку, симметричную точке М относительно середины отрезка АВ.
Задача № 422. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?
Задача № 423. Какие из следующих букв имеют центр симметрии: А, О, М, X, К?
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат. Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.
Параллелограмм: свойства и признаки
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные занятия по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Итоговый тест по геометрии. 8 класс.
Какие из следующих утверждений верны? В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
1) Через точку, не лежащую на данной прямой можно провести прямую параллельную этой прямой.
2) Если диагонали параллелSограмма равны, то этот параллелограмм является ромбом.
3) Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
1) Площадь треугольника меньше произведения двух его сторон.
2) Средняя линия трапеции равна сумме её оснований.
3) Серединные перпендикуляры к сторонам треугольника, пересекаются в точке, являющейся центром окружности вписанной в треугольник.
1) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
2) В тупоугольном треугольнике все углы тупые.
3) Все углы ромба равны.
1) Боковые стороны любой трапеции равны.
2) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
3) Диагональ трапеции делит её на два равных треугольника.
1) Любой прямоугольник можно вписать в окружность.
2) Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.
3) Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
1) Площадь трапеции равна произведению основания трапеции на высоту.
2) Любой квадрат является прямоугольником.
3) Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то этот четырёхугольник является квадратом.
1) Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом.
2) Диагональ равнобедренной трапеции делит её на два равных треугольника.
3) Средняя линия трапеции равна сумме её оснований.
1) В любой ромб можно вписать окружность.
2) Около любого ромба можно описать окружность.
3) Тангенс любого острого угла меньше единицы.
1) Все квадраты имеют равные площади.
2) Любой прямоугольник является квадратом.
3) Около любого прямоугольника можно описать окружность.
Квадрат, его свойства и признаки.
Ищем педагогов в команду «Инфоурок»
Квадрат, его свойства и признаки.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Для квадрата можно ввести несколько определений. Самое ёмкое мы уже привели. Но можно определить квадрат следующим образом:
Квадратом называется четырёхугольник, у которого все стороны равны, а углы прямые.
Квадратом называется параллелограмм, у которого все стороны и углы равны.
Квадратом называется ромб, у которого все углы прямые.
Поскольку квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает теми же свойствами, что и все перечисленные четырёхугольники.
У квадрата диагонали пересекаются и точкой пересечения делятся пополам.
У квадрата диагонали взаимно перпендикулярны.
У квадрата диагонали являются биссектрисами его углов.
У квадрата диагонали равны.
У квадрата стороны являются высотами.
Каждая диагональ квадрата делит его на равные прямоугольные треугольники.
Теперь определим признаки квадрата.
ТЕОРЕМА ( I признак). Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Так как – прямоугольник, то у него противолежащие стороны равны.
– квадрат (по определению), ч.т.д.
ТЕОРЕМА ( II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
по свойству диагоналей прямоугольника, значит, – медиана (по опред-нию).
ТЕОРЕМА ( III признак). Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
ТЕОРЕМА ( IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.
ТЕОРЕМА ( V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
ТЕОРЕМА ( VI признак). Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
2. Так как , то параллелограмм является квадратом (по V признаку квадрата), ч.т.д.
ТЕОРЕМА ( VII признак). Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
1. Так как , то четырёхугольник является ромбом (по V признаку ромба).
Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
Если в ромбе диагонали равны, то этот ромб является квадратом.
Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
В четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что отрезки, соединяющие середины противоположных сторон, равны.
В равнобедренный прямоугольный треугольник, каждый катет которого равен см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.
В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них втрое больше другой и что диагональ квадрата равна дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна см.
Через вершины квадрата проведены прямые, параллельные его диагоналям. Определите вид образованного ими четырёхугольника и вычислите его периметр, если диагональ квадрата равна см.
Найдите периметр квадрата по данным на рисунке.