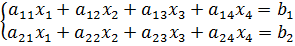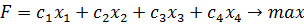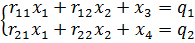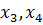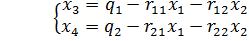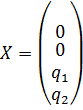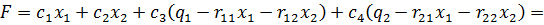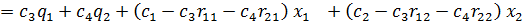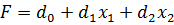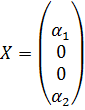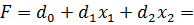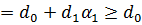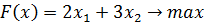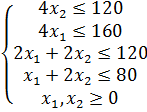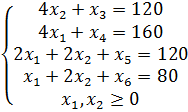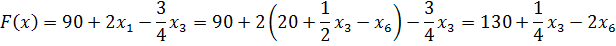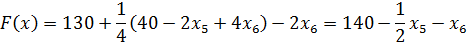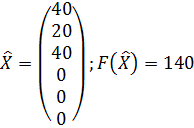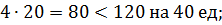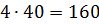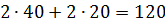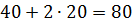если в индексной строке нет отрицательных значений это значит
Симплекс-метод



Каждое оптимальное решение задач линейного программирования находится в угловой точке области ограничений. При малом количестве переменных и ограничений таких точек немного, и вполне возможно вручную найти координаты всех этих точек и подсчитать в них значение целевой функции.
Любое базисное решение, с помощью которого переходят к наиболее оптимальному его варианту, называется опорным решением.
Основные этапы реализации симплекс-метода:
1) указывается способ приведения неканонической задачи к канонической;
2) указывается способ выбора любого опорного решения;
3) устанавливаются критерии оптимальности опорного решения;
4) приводится способ перехода от одного опорного решения к другому, более близкому к оптимальному.
Рассмотрим каноническую задачу линейного программирования для случая, когда значение целевой функции максимизируется:
С помощью элементарных преобразований систему можно привести к виду
В качестве базисных переменных выберем
И тогда базисное решение системы имеет вид
Итак,
Представим все результаты в виде симплекс-таблицы:
| Базис | Цена | План | 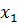 | 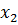 | 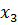 | 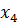 |
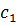 | 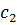 | 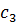 | 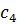 | |||
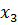 | 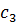 | 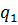 | 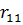 | 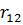 | ||
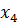 | 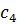 | 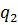 | 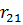 | 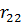 | ||
| F | 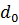 | 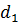 | 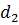 |
Последняя строка в таблице называется индексной строкой.
По индексной строке симплекс-таблицы можно определить, является ли данное решение оптимальным.
Теорема I. Критерий оптимальности плана.
Если в индексной строке симплекс-таблицы нет положительных элементов, то базисный план, соответствующий этой таблице, оптимален.
Доказательство. Действительно, при любых отрицательных 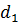
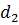
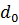
Пусть теперь 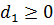
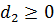
Подставим его в целевую функцию:
Так как нашлось решение, дающее большее значение целевой функции, то при наших предположениях о знаке 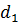
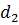
Теорема 2. Критерий улучшения опорного плана.
Если в индексной строке имеется хотя бы один положительный элемент и в столбце над ним также имеется хотя бы один положительный элемент, то базисный план может быть улучшен, т.е. можно найти такое базисное решение, при котором значение целевой функции будет больше.
Теорема 3. Критерий отсутствия оптимального плана.
Если в индексной строке симплекс-таблицы имеется положительное число, а в столбце над ним нет ни одного положительного элемента, то задача оптимального плана не имеет.
Аналогичные теоремы можно привести и для случая, когда целевая функция минимизируется.
Теорема 4. Если в индексной строке симплекс-таблицы нет отрицательных элементов, то базисный план оптимален.
Теорема 5. Если в индексной строке симплекс-таблицы имеется хотя бы одно отрицательное число, а в столбце над ним имеется хотя бы одно положительное, то базисный план может быть улучшен.
Теорема 6. Если в индексной строке симплекс-таблицы имеется отрицательное число, а в столбце над ним нет ни одного положительного элемента, то задача оптимального плана не имеет.
Замечание. Переход к новому базису осуществляется с помощью линейных операций над уравнениями системы.
1. Привести задачу линейного программирования к канонической, вводя балансовые переменные.
2. Занести данные математической модели в симплекс-таблицу.
2.2. Число базисных переменных должно совпадать с числом уравнений в системе ограничений.
2.3. Если в первоначальной таблице нет достаточного количества базисных переменных, над строками выполняются соответствующие элементарные преобразования.
3. Сделать анализ индексной строки:
3.1. Если в индексной строке имеются только отрицательные числа (только положительные) и нули, то данная таблица представляет собой оптимальный план решения задачи на максимум (на минимум): базисным переменным ставится в соответствие число из столбца «План», все остальные переменные обращаются в ноль.
3.2. Если в индексной строке имеется хотя бы одно положительное (отрицательное) число, а в столбце над ним найдется хотя бы один положительный элемент, то базисный план может быть улучшен. Улучшение производится путем перевода основных переменных в базисные с помощью элементарных преобразований над строками расширенной матрицы системы.
3.3. Если в индексной строке имеется хотя бы одно положительное (отрицательное) число, а в столбце над ним нет ни одного положительного элемента, то задача оптимального решения не имеет.
Пример. Для изготовления шкафов и буфетов деревообрабатывающий завод использует древесину четырех видов.
| Вид древесины | Запас | Количество древесины на единицу продукции |
| Шкаф | Буфет | |
| Прибыль |
В таблице указаны запасы древесины, технологические коэффициенты и прибыль от продажи одного буфета и шкафа.
Составить такой план выпуска изделий, при котором прибыль предприятия будет максимальной.
Приведем задачу к канонической, введя балансовые переменные:
Заполним первую симплекс-таблицу. В базис отправлены балансовые переменные, так как их столбцы представляют собой единичные базисные векторы. В индексной строке имеется два положительных числа и над ними также есть положительные элементы. То есть, данный план может быть улучшен. Выберем наибольшее из положительных чисел в индексной строке и отметим его (это число 3). А в столбце над ним найдем такое число, для которого отношение плановой цифры к нему будет наименьшим (это число 4).
| Б | Ц | П | 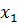 | 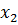 | 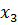 | 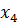 | 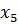 | 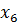 | 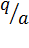 | д |
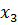 | 30(min) | |||||||||
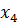 | ||||||||||
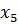 | +I*(-1/2) | |||||||||
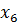 | +I*(1/2) | |||||||||
| F | 3 |
Чтобы получить элементы индексной строки, подставим в целевую функцию новый базисный вектор:
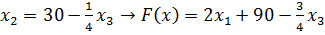
| Б | Ц | П | 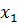 | 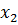 | 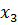 | 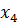 | 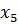 | 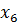 | 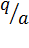 | д |
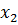 | 1/4 | |||||||||
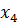 | 160:4=40 | |||||||||
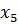 | -1/2 | 60:2=30 | +IV*(-4) | |||||||
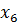 | -1/2 | 20:1=20 | +IV*(-4) | |||||||
| F | 2 | -3/4 |
Видим, что в индексной строке появилось отрицательное число (-3/4). Но еще остался положительный элемент (2). И в столбце 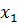
| Б | Ц | П | 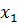 | 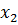 | 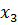 | 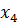 | 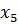 | 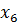 | д |
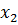 | 1/4 | +III*(1/2) | |||||||
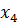 | +III*(-4) | ||||||||
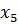 | 1/2 | ||||||||
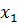 | -1/2 | +III | |||||||
| F | 1/4 | -2 |
Отмечаем, что в индексной строке имеется положительное число, также и в столбце над ним есть положительные элементы. Преобразуем столбец по известному алгоритму.
| Б | Ц | П | 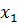 | 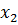 | 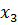 | 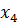 | 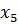 | 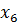 | д |
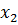 | -1/2 | +III*(1/2) | |||||||
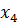 | -4 | +III*(-4) | |||||||
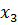 | -4 | ||||||||
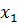 | -1 | +III | |||||||
| F | -1/2 | -1 |
В индексной строке только отрицательные числа и нули. Следовательно, план в данной таблице оптимален. Целевая функция будет принимать значение 140 при значениях переменных базисного столбца, равных соответствующим значениям столбца «План».
Проведем экономический анализ задачи. Подставим полученные значения переменных в систему ограничений;
Видим, что при плане изготовления 40 шкафов и 20 буфетов древесина II, III, IV видов будет использована полностью, а 40 единиц древесины I вида останется. Этот остаток и соответствует балансовой переменной
Замечание. Так как в задаче всего две основных переменных, она могла быть решена и графически (см. пример 1 п. 3.1).
Задачи линейного программирования могут иметь не единственное решение.
Теорема (о бесконечном множестве оптимальных планов)
Если в индексной строке симплекс-таблицы, содержащей оптимальный план, имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то задача линейного программирования имеет бесконечное множество оптимальных планов.
Подробный разбор симплекс-метода
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание: Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
Замечание: ≥0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение: Точка называется угловой точкой, если представление
возможно только при
.
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е.
– не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение: Пусть есть система m уравнений и n неизвестных (m
Симплексный метод решения задач линейного программирования
При графическом методе решения задач ЛП мы фактически из множества вершин, принадлежащих границе множества решений системы неравенств, выбрали такую вершину, в которой значение целевой функции достигало максимума (минимума). В случае двух переменных этот метод совершенно нагляден и позволяет быстро находить решение задачи.
Если в задаче три и более переменных, а в реальных экономических задачах как раз такая ситуация, трудно представить наглядно область решений системы ограничений. Такие задачи решаются с помощью симплекс-метода или методом последовательных улучшений. Идея метода проста и заключается в следующем.
Рассмотрим симплексный метод на конкретном примере задачи о составлении плана.
Еще раз заметим, что симплекс-метод применим для решения канонических задач ЛП, приведенных к специальному виду, т. е. имеющих базис, положительные правые части и целевую функцию, выраженную через небазисные переменные. Если задача не приведена к специальному виду, то нужны дополнительные шаги, о которых мы поговорим позже.
Рассмотрим задачу о плане производства, предварительно построив модель и приведя ее к специальному виду.
Эта задача имеет специальный вид (с базисом, правые части неотрицательны). Ее можно решить симплекс-методом.
II этап. Проверка опорного плана на оптимальность.
Данной таблице 3.4 соответствует следующий опорный план:
Возможны различные ситуации.
1. В индексной F-строке нет отрицательных элементов. Значит, план оптимален, можно выписать решение задачи. Целевая функция достигла своего оптимального значения, равного числу, стоящему в правом нижнем углу, взятому с противоположным знаком. Переходим к IV этапу.
2. В индексной строке есть хотя бы один отрицательный элемент, в столбце которого нет положительных. Тогда делаем вывод о том, что целевая функция F→∞ неограниченно убывает.
3. В индексной строке есть отрицательный элемент, в столбце которого есть хотя бы один положительный. Тогда переходим к следующему III этапу. пересчитываем таблицу, улучшая опорный план.
III этап. Улучшение опорного плана.
Из отрицательных элементов индексной F-строки выберем наибольший по модулю, назовем соответствующий ему столбец разрешающим и пометим «↑».
Чтобы выбрать разрешающую строку, необходимо вычислить отношения элементов столбца свободных членов только к положительным элементам разрешающего столбца. Выбрать из полученных отношений минимальное. Соответствующий элемент, на котором достигается минимум, называется разрешающим. Будем выделять его квадратом.
Выбрав разрешающий элемент, делаем перечет таблицы по правилам:
1. В новой таблице таких же размеров, что и ранее, переменные разрешающей строки и столбца меняются местами, что соответствует переходу к новому базису. В нашем примере: х1 входит в базис, вместо х5, которая выходит из базиса и теперь свободная (табл. 3.6).
2. На месте разрешающего элемента 2 записываем обратное ему число ½.
3. Элементы разрешающей строки делим на разрешающий элемент.
4. Элементы разрешающего столбца делим на разрешающий элемент и записываем с противоположным знаком.
5. Чтобы заполнить оставшиеся элементы таблицы 3.6, осуществляем пересчет по правилу прямоугольника. Пусть мы хотим посчитать элемент, стоящий на месте 50.
Соединяем этот элемент мысленно с разрешающим, находим произведение, вычитаем произведение элементов, находящихся на другой диагонали получившегося прямоугольника. Разность делим на разрешающий элемент.
Итак, 




После пересчета таблицы убеждаемся, что в индексной строке нет отрицательных элементов, следовательно, задача решена, базисный план оптимален.
IVэтап. Выписывание оптимального решения.
— необходимо в план выпуска включить 20 изделий типа А, 40 изделий типа В, при этом прибыль будет максимальной и будет равна 220 руб.
В конце этого параграфа приведем блок-схему алгоритма симплекс-метода, которая в точности повторяет этапы, но, возможно, для некоторых читателей будет более удобна в пользовании, т. к. стрелочки указывают четкую направленность действий.
Ссылки над прямоугольниками в блок-схеме показывают, к какому этапу или подпункту относится соответствующая группа преобразований. правило нахождения первоначального опорного плана будет сформулировано в пункте 3.7.