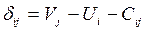если в транспортной задаче объем спроса равен объему предложения то такая задача называется
Тест с ответами Линейное программирование
I вариант.
1. Модель – это
а) аналог (образ) оригинала, но построенный средствами и методами отличными от оригинала +
б) подобие оригинала
в) копия оригинала
2. Экономико-математическая модель – это
а) математическое представление экономической системы (объектов, задачи, явлений, процессов и т. п.) +
б) качественный анализ и интуитивное представление объектов, задач, явлений, процессов экономической системы и ее параметров
в) эвристические описание экономической системы (объектов, задачи, явлений, процессов и т. п.)
3. Метод – это
а) подходы, пути и способы постановки и решения той или иной задачи в различных областях человеческой деятельности +
б) описание особенностей задачи (проблемы) и условий ее решения
в) требования к условиям решения той или иной задачи
4. Выберите неверное утверждение
а) ЭММ позволяют сделать вывод о поведении объекта в будущем
б) ЭММ позволяют управлять объектом +
в) ЭММ позволяют выявить оптимальный способ действия
г) ЭММ позволяют выявить и формально описать связи между переменными, которые характеризуют исследования
5. Экономико-математическая модель межотраслевого баланса – это
а) макроэкономическая, детерминированная, имитационная, матричная модель
б) микроэкономическая, детерминированная, балансовая, регрессионная модель
в) макроэкономическая, детерминированная, балансовая, матричная + модель
г) макроэкономическая, вероятностная, имитационная, матричная модель
6. Найти экстремум функции f(x) при выполнении ограничений Ri(x) = ai, φ (x) ≤ bj, наложенных на параметры функции – это задача
а) условной оптимизации +
б) линейного программирования
в) безусловной оптимизации
г) нелинейного программирования
д) динамического программирования
7. Задача, включающая целевую функцию f и функции Ф, входящие в ограничения, является задачей линейного программирования, если
а) все Ф и f являются линейными функциями относительно своих аргументов +
б) все Ф являются линейными функциями относительно своих аргументов, а функция f – нелинейна
в) функция f является линейной относительно своих аргументов, а функции Ф – нелинейны
г) только часть функций Ф и функция f являются линейными относительно своих аргументов
8. Множество всех допустимых решений системы задачи линейного программирования
а) является
б) выпуклым +
в) вогнутым
г) одновременно выпуклым и вогнутым
9. Если задача линейного программирования имеет оптимальное решение, то целевая функция достигает нужного экстремального значения в одной из:
а) вершин многоугольника (многогранника) допустимых решений +
б) внутренних точек многоугольника (многогранника) допустимых решений
в) точек многоугольника (многогранника) допустимых решений
10. В задачах линейного программирования решаемых симплекс-методом искомые переменные должны быть
а) Неотрицательными +
б) положительными
в) свободными от ограничений
г) любыми
11. Симплексный метод решения задач линейного программирования включает:
а) определение одного из допустимых базисных решений поставленной задачи (опорного плана)
б) определение правила перехода к не худшему решению
в) проверку оптимальности найденного решения
г) определение одного из допустимых базисных решений поставленной задачи (опорного плана), определение правила перехода к не худшему решению, проверка оптимальности найденного решения +
12. Задача линейного программирования не имеет конечного оптимума, если
а) в точке А области допустимых значений достигается максимум целевой функции F
б) в точке А области допустимых значений достигается минимум целевой функции F
в) система ограничений задачи несовместна
г) целевая функция не ограничена сверху на множестве допустимых решений +
13. При приведении задачи линейного программирования (ЛП) к виду основной задачи ЛП ограничения вида «
Если в транспортной задаче объем спроса равен объему предложения то такая задача называется
Авторизация
Сайты партнеры:
Для быстрого поиска по странице используйте комбинацию клавиш Ctrl+F и в появившемся окне напечатайте слово запроса (или первые буквы)
Линейное программирование
Модель – это
аналог (образ) оригинала, но построенный средствами и методами отличными от оригинала
подобие оригинала
копия оригинала
Экономико-математическая модель – это
математическое представление экономической системы (объектов, задачи, явлений, процессов и т. п.)
качественный анализ и интуитивное представление объектов, задач, явлений, процессов экономической системы и ее параметров
эвристические описание экономической системы (объектов, задачи, явлений, процессов и т. п.)
Метод – это
подходы, пути и способы постановки и решения той или иной задачи в различных областях человеческой деятельности
описание особенностей задачи (проблемы) и условий ее решения
требования к условиям решения той или иной задачи
ЭММ позволяют
сделать вывод о поведении объекта в будущем
управлять объектом
выявить оптимальный способ действия
выявить и формально описать связи между переменными, которые характеризуют исследования
Экономико-математическая модель межотраслевого баланса – это
макроэкономическая, детерминированная, имитационная, матричная модель
микроэкономическая, детерминированная, балансовая, регрессионная модель
макроэкономическая, детерминированная, балансовая, матричная модель
макроэкономическая, вероятностная, имитационная, матричная модель
Найти экстремум функции f(x) при выполнении ограничений Ri(x) = ai, φ (x) ≤ bj, наложенных на параметры функции – это задача
условной оптимизации
линейного программирования
безусловной оптимизации
нелинейного программирования
динамического программирования
Задача, включающая целевую функцию f и функции Ф, входящие в ограничения, является задачей линейного программирования, если
все Ф и f являются линейными функциями относительно своих аргументов
все Ф являются линейными функциями относительно своих аргументов, а функция f – нелинейна
функция f является линейной относительно своих аргументов, а функции Ф – нелинейны
только часть функций Ф и функция f являются линейными относительно своих аргументов
Множество всех допустимых решений системы задачи линейного программирования является
выпуклым
вогнутым
одновременно выпуклым и вогнутым
Если задача линейного программирования имеет оптимальное решение, то целевая функция достигает нужного экстремального значения в одной из
вершин многоугольника (многогранника) допустимых решений
внутренних точек многоугольника (многогранника) допустимых решений
точек многоугольника (многогранника) допустимых решений
В задачах линейного программирования решаемых симплекс-методом искомые переменные должны быть
Неотрицательными
положительными
свободными от ограничений
любыми
Симплексный метод решения задач линейного программирования включает
определение одного из допустимых базисных решений поставленной задачи (опорного плана)
определение правила перехода к не худшему решению
проверку оптимальности найденного решения
определение одного из допустимых базисных решений поставленной задачи (опорного плана), определение правила перехода к не худшему решению, проверка оптимальности найденного решения
Графический способ решения задачи линейного программирования – это
построение прямых, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств
нахождение полуплоскости, определяемой каждым из ограничений задачи
нахождение многоугольника допустимых решений
построение прямой F = h = const >= 0, проходящей через многоугольник решений
построение вектора C, перпендикулярного прямой F = h = const
передвижение прямой F = h = const в направлении вектора C (в сторону увеличения h), в результате чего находят либо точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве допустимых решений
определение координат точки максимума функции и вычисление значения целевой функции в этой точке
Задача линейного программирования не имеет конечного оптимума, если
в точке А области допустимых значений достигается максимум целевой функции F
в точке А области допустимых значений достигается минимум целевой функции F
система ограничений задачи несовместна
целевая функция не ограничена сверху на множестве допустимых решений
Постановка статической транспортной задачи линейного программирования. Сущность и алгоритм метода потенциалов решения транспортной задачи линейного программирования в матричной постановке
Страницы работы
Содержание работы
44. Постановка статической транспортной задачи линейного программирования. Сущность и алгоритм метода потенциалов решения транспортной задачи линейного программирования в матричной постановке
В процессе решения транспортной задачи линейного программирования (ТЗЛП) составляется оптимальный план перевозок груза в замкнутой транспортной системе, состоящей из нескольких поставщиков и потребителей. Каждый поставщик в такой транспортной системе соединен с каждым потребителем транспортной связью. Каждая транспортная связь характеризуется опр-ой дальностью или стоимостью (оценкой) перевозки по ней единицы груза.
В процессе реш ТЗ требуется максимальные объемы перевозок перерасн-ть между наиболее дешевыми транс.связями так, чтобы полностью вывезти продукцию от всех поставщиков и удовлет-ть спрос всех потребителей.
Необходимым условием решения ТЗЛП является закрытость или замкнутость моделируемой транспортной системы. В замкнутой задаче объемы спроса равны объемам потребления. Если это условие нарушается, то транспортная задача называется «открытой» и приводится к задаче закрытого типа путем введения в транспортную систему дополнит. (фиктивного) поставщика или потребителя. Этому фиктивному поставщику или потребителю приписываются соответственно недостающий объем предложения или спроса, в результате чего система становится закрытой. Кроме того, естественным ограничением в ТЗЛП является условие неотрицательности объемов перевозок.
Идея метода потенциалов заключается в том, что отличия затрат на перевозку по разным транспортным связям можно представить как разность потенциалов, причем эта разность потенциалов будет тем больше, чем сильнее различаются величины затрат.
Алгоритм метода потенциалов, применяемого при решении транспортной задачи линейного программирования (ТЗЛП), состоит из следующих действий:
2) построение начального (базисного) плана перевозок. Для построения базисного плана в ТЗЛП существует несколько методов, наиболее распространенными из которых являются метод «северо-западного угла» и метод наименьшей стоимости. По методу «северо-западного угла» распределение объемов перевозок начинается с верхней левой клетки матрицы. В нее помещается минимальное из двух значений: объем производства первого поставщика; объем спроса первого потребителя. Если объем предложения первого поставщика превышает спрос первого потребителя, то излишки продукции отправляются второму потребителю. И наоборот, если объем спроса первого потребителя превосходит возможности первого поставщика, то недостающий объем поставляется от второго поставщика. Объемы производства остальных поставщиков распределяются аналогичным образом. Метод наименьшей стоимости отличается от метода «северо-западного угла» тем, что перевозки в нем в первую очередь распределяются по клеткам с наименьшей оценкой. Количество заполненных перевозками клеток должно быть на единицу меньше суммы количества поставщиков и потребителей. В противном случае возникает случай вырождения, затрудняющий решение ТЗЛП, поэтому необходимо так перераспределить перевозки в базисном плане, чтобы их количество удовлетворяло указанному условию;
3) построение системы потенциалов( это условные числа, приписываемые каждому поставщику и потребителю). Потенциалы связаны со стоимостью существующих в плане перевозок. Потенциал рассчитывается как сумма потенциалов строки и стоимости перевозки для занятой клетки. И наоборот ( 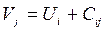
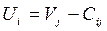
4) расчет разности потенциалов (положительных сдвижек) для клеток, не загруженных перевозками (свободных клеток). Величина положительной сдвижки равна разности между потенциалом строки, потенциалом столбца и оценки свободной клетки, находящейся на их пересечении. Если положительные сдвижки (значение которых больше 0) отсутствуют, то оптимальный план перевозок найден;
6) проверить правильность вычислений. Для этого достаточно сравнить суммарные затраты на перевозку груза по новому плану с затратами базисного (или предыдущего) плана перевозок. Уменьшение затрат является признаком правильности вычислений. Итерации повторяются с пункта 3 до тех пор, пока имеется хотя бы одна положительная сдвижка.
Теория линейное программирование — тест с ответами
Математика дается не всем. Но сдавать её нужно чтобы получить за нее зачет или какую либо оценку. Сейчас чаще всего проводится проверка знаний в виде тестирования. Мы собрали частые вопросы встречающиеся в тестах на этой странице. Обратите внимание что правильные варианты ответов выделены символом [+].
Если в прямой задаче, какое либо ограничение является неравенством, то в двойственной задаче соответствующая переменная
[-] в) свободна от ограничений
Транспортная задача является задачей …. Программирования
Если в транспортной задаче объем спроса равен объему предложения, то такая задача называется
Если в транспортной задаче объем запасов превышает объем потребностей, в рассмотрение вводят
[-] а) фиктивный пункт производства
[+] б) фиктивный пункт потребления
[-] в) изменения структуры не требуются
Методы теории игр предназначены для решения задач
[+] а) с конфликтными ситуациями в условиях неопределенности
[-] б) с полностью детерминированными условиями
[-] в) статистического моделирования
Стратегия игрока – это совокупность правил, определяющих выбор его действий при
[+] а) каждом ходе в зависимости от сложившейся ситуации в одном сеансе игры
[-] в) всех сеансах игры
Нижняя цена игры – это
[+] а) максимин, т.е. максимальный выигрыш по всем стратегиям одного из игроков среди минимальных значений выигрышей каждой его стратегии
[-] б) гарантированный выигрыш одного из игроков при любой стратегии другого игрока
[-] в) минимакс, т.е. минимальный проигрыш по всем стратегиям одного из игроков среди максимальных значений проигрышей каждой его стратегии
Верхняя цена игры – это
[+] а) минимакс, т.е. минимальный проигрыш по всем стратегиям одного из игроков среди максимальных значений проигрышей каждой его стратегии
[-] б) гарантированный проигрыш одного из игроков при любой стратегии другого игрока
[-] в) максимин, т.е. максимальный выигрыш по всем стратегиям одного из игроков среди минимальных значений выигрышей каждой его стратегии
Решение игры в чистых стратегиях определяется
[-] а) ценой игры, равной нижней цене игры
[-] б) ценой игры, равной верхней цене игры
[-] в) наличием седловой точки
[+] г) всем перечисленным в ответах на это задание
Решение игры в смешанных стратегиях определяется
[+] а) вероятностью выбора каждой из активных (полезных) стратегий, совокупный выигрыш которых представляет случайную величину с математическим ожиданием равным цене игры
[-] б) ценой игры, равной нижней цене игры
[-] в) ценой игры, равной верхней цене игры
[-] г) наличием седловой точки
Задача, процесс нахождения решения которой является многоэтапным, относится к задачам
[-] а) линейного программирования
[+] в) динамического программирования
[-] г) нелинейного программирования
д) параметрического программирования
Определите, что включает симплексный метод решения задач линейного программирования:
[-] а) определение одного из допустимых базисных решений поставленной задачи (опорного плана)
[-] б) определение правила перехода к не худшему решению проверку оптимальности найденного решения
[+] в) определение одного из допустимых базисных решений поставленной задачи (опорного плана), определение правила перехода к не худшему решению, проверка оптимальности найденного решения
Выберите правильный вариант. Задача линейного программирования не имеет конечного оптимума, если:
[-] а) в точке А области допустимых значений достигается максимум целевой функции F
[-] б) в точке А области допустимых значений достигается минимум целевой функции F
[-] в) система ограничений задачи несовместна
[+] г) целевая функция не ограничена сверху на множестве допустимых решений
Как называется модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой уравнений?
Что должно быть в линейных оптимизационных моделях, решаемых с помощью геометрических построений число переменных?
[-] г) не больше числа ограничений +2
Отметьте, какое максимальное значение может достигать задача линейного программирования?
[-] а) только в одной точке
[+] в) во множестве точек
[-] г) в одной или двух точках
д) в одной или во множестве точек
Выберите верный вариант. Если в прямой задаче, какое либо ограничение является неравенством, то в двойственной задаче соответствующая переменная:
[-] в) свободна от ограничений
Вставьте пропущенное слово. Транспортная задача является задачей ___________ программирования.
Как называется задача, если в транспортной задаче объем спроса равен объему предложения:
Выберите верный вариант. Если в транспортной задаче объем запасов превышает объем потребностей, в рассмотрение вводят:
[-] а) фиктивный пункт производства
[+] б) фиктивный пункт потребления
[-] в) изменения структуры не требуются
Тест по разделу МДК 02.01.01 «Линейное программирование»
Ищем педагогов в команду «Инфоурок»
1. Модель – это
1) аналог (образ) оригинала, но построенный средствами и методами отличными от оригинала +
2) подобие оригинала
3)копия оригинала
2. Экономико-математическая модель – это
1) математическое представление экономической системы (объектов, задачи, явлений, процессов и т. п.) +
2) качественный анализ и интуитивное представление объектов, задач, явлений, процессов экономической системы и ее параметров
3) эвристические описание экономической системы (объектов, задачи, явлений, процессов и т. п.)
3. Метод – это
1) подходы, пути и способы постановки и решения той или иной задачи в различных областях человеческой деятельности +
2) описание особенностей задачи (проблемы) и условий ее решения
3) требования к условиям решения той или иной задачи
4. Задача, включающая целевую функцию f и функции Ф, входящие в 1) ограничения, является задачей линейного программирования, если
1) все Ф и f являются линейными функциями относительно своих аргументов +
2) все Ф являются линейными функциями относительно своих аргументов, а функция f – нелинейна
3) функция f является линейной относительно своих аргументов, а функции Ф – нелинейны
4) только часть функций Ф и функция f являются линейными относительно своих аргументов
5. Множество всех допустимых решений системы задачи линейного программирования является
1) выпуклым +
2) вогнутым
3) одновременно выпуклым и вогнутым
6. Если задача линейного программирования имеет оптимальное решение, то целевая функция достигает нужного экстремального значения в одной из
1) вершин многоугольника (многогранника) допустимых решений +
2) внутренних точек многоугольника (многогранника) допустимых решений
3) точек многоугольника (многогранника) допустимых решений
7. В задачах линейного программирования решаемых симплекс-методом искомые переменные должны быть
1) неотрицательными +
2) положительными
3) свободными от ограничений
4) любыми
8. Симплексный метод решения задач линейного программирования включает
1) определение одного из допустимых базисных решений поставленной задачи (опорного плана)
2) определение правила перехода к не худшему решению
проверку оптимальности найденного решения
3) определение одного из допустимых базисных решений поставленной задачи (опорного плана), определение правила перехода к не худшему решению, проверка оптимальности найденного решения +
9. Графический способ решения задачи линейного программирования – это
1) построение прямых, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств
2) нахождение полуплоскости, определяемой каждым из ограничений задачи
3) нахождение многоугольника допустимых решений
4) построение прямой F = h = const >= 0, проходящей через многоугольник решений
5) построение вектора C, перпендикулярного прямой F = h = const
6) передвижение прямой F = h = const в направлении вектора C (в сторону увеличения h), в результате чего находят либо точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве допустимых решений
7) определение координат точки максимума функции и вычисление значения целевой функции в этой точке
8) все перечисленные ответы в этом задании +
10. Задача линейного программирования не имеет конечного оптимума, если
1) в точке А области допустимых значений достигается максимум целевой функции F
2) в точке А области допустимых значений достигается минимум целевой функции F
3) система ограничений задачи несовместна
4) целевая функция не ограничена сверху на множестве допустимых решений +
11. Модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой уравнений, называется
1) стандартной
2) канонической +
3) общей
4) основной
5) нормальной
12. В линейных оптимизационных моделях, решаемых с помощью геометрических построений число переменных должно быть
1) не больше двух +
2) равно двум
3) не меньше двух
4) не больше числа ограничений +2
5) сколько угодно
13. Задача линейного программирования может достигать максимального значения
1) только в одной точке
2) в двух точках
3) во множестве точек +
4) в одной или двух точках
5) в одной или во множестве точек
14. Если в прямой задаче, какое либо ограничение является неравенством, то в двойственной задаче соответствующая переменная
1) неотрицательна +
2) положительна
3) свободна от ограничений
4) отрицательная
15. Транспортная задача является задачей …. Программирования
1) динамического
2) нелинейного
3) линейного +
4) целочисленного
5) параметрического
16. Если в транспортной задаче объем спроса равен объему предложения, то такая задача называется
1) замкнутой
2) закрытой +
3) сбалансированной
4) открытой
5) незамкнутой
17. Если в транспортной задаче объем запасов превышает объем потребностей, в рассмотрение вводят
1) фиктивный пункт производства
2) фиктивный пункт потребления +
3) изменения структуры не требуются