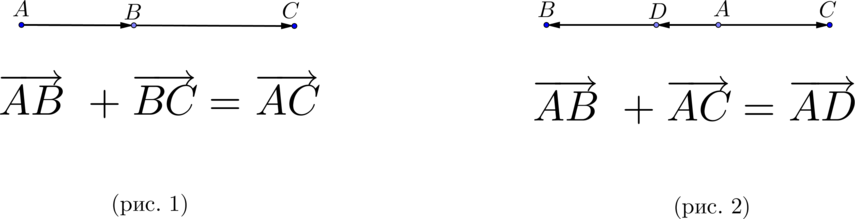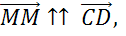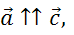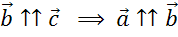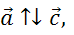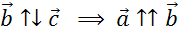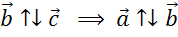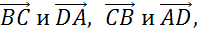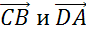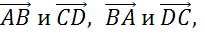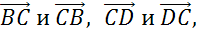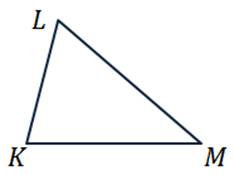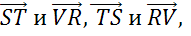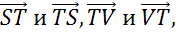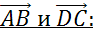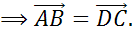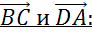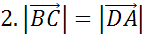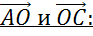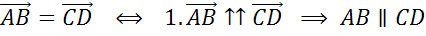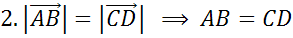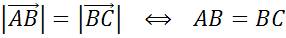если векторы сонаправлены и их длины равны то такие векторы называют
Вектор. Виды векторов.
Вектор — в самом элементарном случае это математический объект, который характеризуется
величиной и направлением.
В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая
из его граничных точек является началом, а какая — концом.
У вектора есть длина и определенное направление. Графически вектора изображаются как
направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.
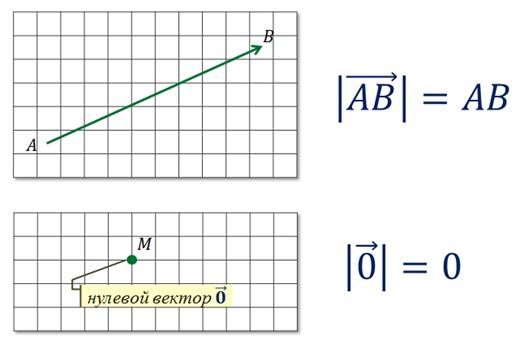
Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.
Как видно на рисунке, начало отрезка – это точка А, концом отрезка является
точка В, а непосредственно вектор обозначен через 
вектора существенное значение, если переместить стрелку на другую
сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора
удобно сравнивать с движением физического тела: подумайте, ехать на
рыбалку и с рыбалки – разница огромная.

Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть
разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.
Виды векторов.
Единичным называется вектор, длина которого равна 1.
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.
У такого вектора конец и начало совпадают.
Нулевой вектор обычно обозначается как 
Коллинеарные вектора – вектора, которые параллельны одной прямой
или которые лежат на одной прямой.
Сонаправленные вектора. Два коллинеарных вектора a и b называются
сонаправленными векторами только тогда, когда их направления
соответствуют друг другу: a↑↑b

Противоположно направленные вектора – два коллинеарных вектора
a и b называются противоположно направленными векторами, только
когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной
плоскости или те, которые лежат на общей плоскости.
В любое мгновение существует плоскость одновременно параллельную
двум любым векторам, поэтому два произвольных вектора являются

Равные вектора. Вектора a и b будут равными, если они будут лежать на
одной либо параллельных прямых и их направления и длины одинаковые.
То есть, такой вектор можно перенести параллельно ему в каждое место
Таким образом, два вектора равны, если они коллинеарные, сонаправленые
и имеют одинаковые длины:

Для координатного представления векторов огромное значение
оказывает понятие проекции вектора на ось (направленную
прямую).
проекциями точек начала и конца вектора на заданную прямую,
при этом проекции добавляется знак “+”, но когда направление
проекции соответственно направлению оси, иначе — знак “–”.

Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция
вектора на ось, которая перпендикулярна ему = 0.
Когда работают с векторами, зачастую вводят так называемую
декартову систему координат и уже в этой системе находят
координаты вектора по базисным векторам.
Разложение по базису геометрически можно показать проекцией
вектора на координатные оси. Когда известны координаты начала и
конца вектора, то координаты данного вектора получают вычитая
из координат конца вектора координат начала вектора.

За базис зачастую выбираются координатные орты, которые обозначаются как 
осям x, y, z. Исходя из этого, вектор 
Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование
из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,
кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только
те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).
Векторы. Начальные сведения
Определения
Если длина вектора равна нулю (совпадают начало и конец), то такой вектор называют нулевым.
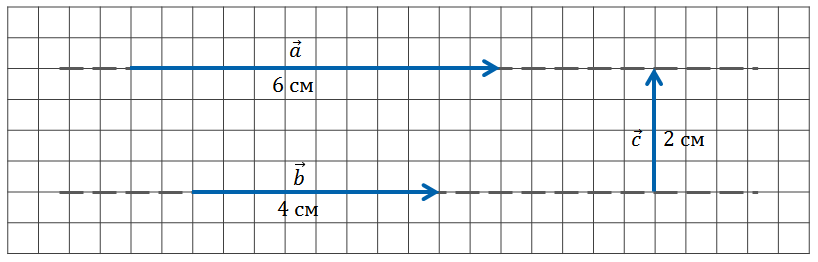
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых ( \(\overrightarrow a, \overrightarrow b\) и \(\overrightarrow c\) ).
В противном случае векторы называются неколлинеарными (например, \(\overrightarrow a\) и \(\overrightarrow d\) ).
Векторы называются равными, если они сонаправлены и их длины равны.
Правила сложения коллинеарных векторов:
\(\blacktriangleright\) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).
\(\blacktriangleright\) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).
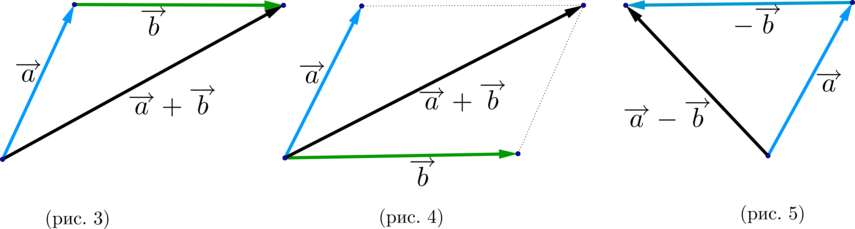
Правила сложения неколлинеарных векторов \(\overrightarrow \) и \(\overrightarrow\) :
\(\blacktriangleright\) Правило треугольника (рис. 3).
\(\blacktriangleright\) Правило параллелограмма (рис. 4).
Определение
Вектор \(\overrightarrow <-b>\) – это вектор, противоположно направленный с вектором \(\overrightarrow \) и совпадающий с ним по длине.
Свойства сложения векторов
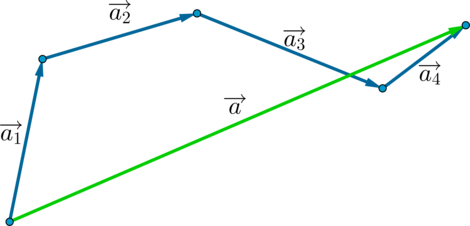
Замечание
Для того, чтобы сложить несколько вектором, можно отложить их последовательно: каждый следующий от конца предыдущего. Тогда суммой этих векторов будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего: \[\overrightarrow
Определение
Свойства произведения вектора на число
1. Сочетательный закон: \(k(\lambda\overrightarrow )=(k\lambda)\overrightarrow \) ;
Теорема
Векторы, имеющие равные длины
Рассмотрим векторы, имеющие равные длины. Если такие векторы сонаправлены, их называют равными.
У равных векторов совпадает и длина и направление.
Векторы, направленные в противоположные стороны, даже, если у них будут равные длины, равными назвать не получится.
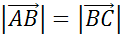
Если совпадает только одна характеристика — длина, то векторы называют равными по модулю.
Равные векторы
Если два вектора равны (т. е. одинаковые), то у них одинаковые:
Рассмотрим рисунок 1. На рисунке представлены векторы, обозначенные красным и зеленым цветом. Видно, что векторы имеют равные координаты — проекции на оси. Длины проекций для этих векторов: на ось Ox = 2, на ось Oy = 3. Если векторы имеют равные соответственные проекции (координаты), то эти векторы равны.
Примечание:
Когда векторы равны, вместо одного из них мы можем использовать второй вектор. Если нам будет удобнее работать со вторым вектором.
Противоположно направленные векторы
Вектор можно развернуть в противоположную сторону. С точки зрения математики, для этого достаточно перед вектором дописать знак минус.
Пример 1:
Когда векторы обозначают двумя буквами, то:
Вектор \( \left(-\overrightarrow
На языке математики это записывают так: \( \left(-\overrightarrow
Для вектора \( \overrightarrow
А для вектора \(\overrightarrow
Когда даны координаты вектора, то, чтобы его развернуть в противоположную сторону, нужно изменить знак каждой его координаты на противоположный.
Пример 2:
Примечание:
Если равны только длины векторов, а направлены они в противоположные стороны, знак равенства между ними записать не получится. Такие векторы не равны!
Физика, равные по модулю противоположно направленне векторы
В физике, в третьем законе Ньютона, идет речь о равных по модулю и противоположно направленных векторах.
Чтобы приравнять такие векторы, необходимо перед одним из них записать знак минус:
Равенство векторов
Урок 2. Геометрия 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Равенство векторов»
Вы уже знакомы с понятием вектора, знаете, что каждый вектор характеризуется направлением и длиной, которая равна длине соответствующего отрезка.
Также с прошлых уроков вам известно, что любая точка плоскости тоже является вектором, нулевым вектором. Длина нулевого вектора всегда равна нулю.
Обладая всеми этими знаниями, мы можем приступить к изучению равных векторов.
Но перед этим введём понятие коллинеарных векторов.
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.
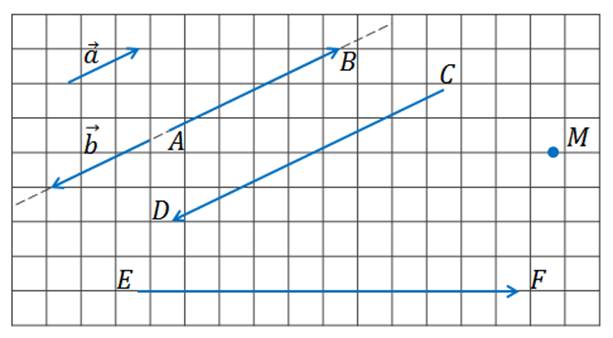
Посмотрим на рисунок и найдём на нём коллинеарные векторы.
Векторы 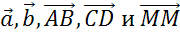
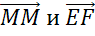
А вот, например, векторы 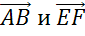
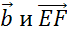
Рассмотрим два коллинеарных вектора 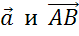
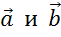
Запомните, в первом случае векторы называют сонаправленными и обозначают их таким знаком 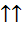
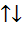
Если говорить о нулевом векторе, то стоит вспомнить, что его начало совпадает с концом. Поэтому он не имеет какого-то определённого направления. Другими словами, любое направление можно считать направлением нулевого вектора. Поэтому нулевой вектор будет сонаправлен с любым вектором. Например, векторы 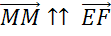
Для ненулевых коллинеарных векторов можно выделить следующие свойства.
Если вектор 
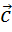

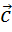


Если вектор 
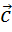

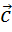


Если вектор 
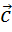

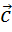


Итак, мы ввели понятие коллинеарных векторов. Узнали, какие векторы называются сонаправленными, а какие — противоположно направленными.
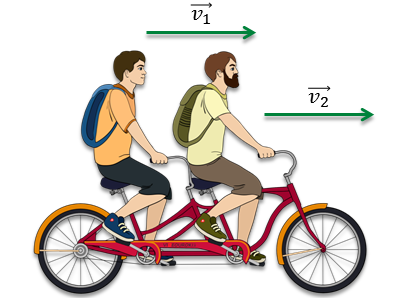
А теперь рассмотрим такой пример. На велосипеде-тандеме едут два туриста. Каждый из них движется в одном и том же направлении и с одной и той же скоростью.
Скорость каждого туриста является векторной величиной, и мы можем изобразить её в виде вектора.
Так как направления движения совпадают и скорости равны, то векторы будут иметь одинаковые направления и равные длины.
Этот пример даёт нам понять, как дать определение равным векторам.
Векторы называют равными, если они сонаправлены и их длины равны.
Равенство векторов обозначают так 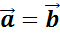
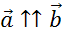
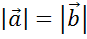
Приступим к решению задач.
Задача. Начертить векторы 

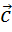


а векторы 
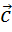


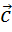
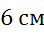
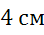
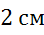
Чтобы векторы 



Вектор 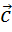

Перейдём к следующей задаче.
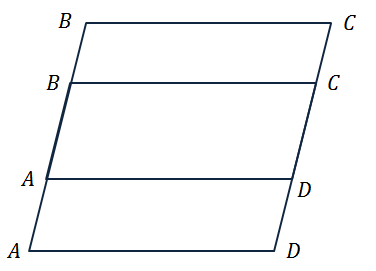
Задача. Выписать пары коллинеарных векторов, которые определяются сторонами:
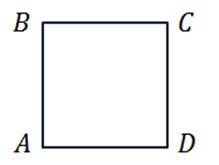
а) квадрата 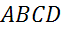
б) треугольника 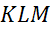
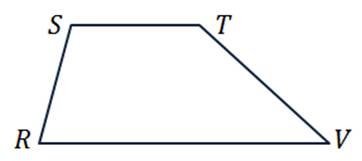
в) трапеции 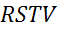
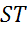
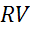
Изобразим квадрат ABCD. Коллинеарные векторы лежат на одной прямой или на параллельных прямых.
Рассмотрим параллельные стороны BC и АD. Можем записать такие пары коллинеарных векторов: 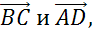
Рассмотрим параллельные стороны AB и CD. Можно записать следующие пары коллинеарных векторов: 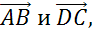
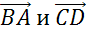
Также коллинеарными будут векторы 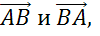
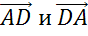
Получили 12 пар коллинеарных векторов.
В следующем пункте изобразим треугольник KLM.
Никакие из его сторон не параллельны. Но коллинеарными будут векторы, лежащие на одной стороне: 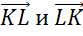
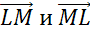
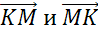
Получили 3 пары коллинеарных векторов.
В последнем пункте изобразим трапецию PSTV так, чтобы стороны ST и PV являлись её основаниями.
Параллельных сторон видим только две, поэтому запишем следующие пары коллинеарных векторов: 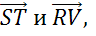
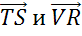
Также коллинеарными будут векторы, лежащие на одной стороне: 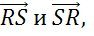
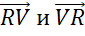
Получили 8 пар коллинеарных векторов.
Рассмотрим следующую задачу.
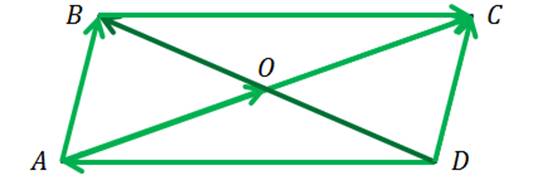
Задача. Диагонали параллелограмма 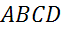
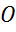
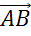
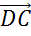
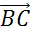
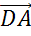
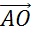
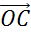
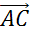
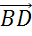
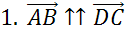
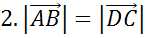
Следующая пара векторов
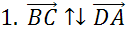
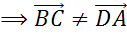
Далее обратим внимание на пару векторов
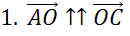
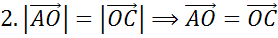
Последней рассмотрим пару векторов
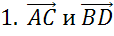
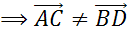
Задача. Определить вид четырёхугольника 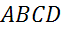
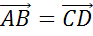
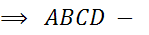
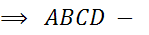
Подведём итоги урока.
Сегодня мы познакомились с понятием коллинеарных векторов. Так называют ненулевые векторы, которые лежат на одной прямой либо на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.
При этом среди коллинеарных векторов мы выделили два случая: сонаправленные векторы (они имеют одинаковое направление) и противоположно направленные векторы (они имеют противоположные направления).
Опираясь на эти знания, мы дали определение равным векторам.
Векторы называют равными, если они сонаправлены и их длины равны.
Эти знания очень важны, они пригодятся вам при решении задач и при дальнейшем изучении векторов.