Гомеоморфно что это значит
Гомеоморфизм
Смотреть что такое «Гомеоморфизм» в других словарях:
гомеоморфизм — гомеоморфизм … Орфографический словарь-справочник
гомеоморфизм — сущ., кол во синонимов: 1 • гомеоморфность (1) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
гомеоморфизм — Морфологическое и иное сходство различных организмов, не связанных между собой непосредственным родством, обусловленное обитанием в сходных условиях; Г. является одним из проявлений конвергенции. [Арефьев В.А., Лисовенко Л.А. Англо русский… … Справочник технического переводчика
Гомеоморфизм — Не следует путать с гомоморфизмом. Классический пример гомеоморфизма: кружка и тор топологически эквивалентны Гомеоморфизм (греч … Википедия
Гомеоморфизм — Митчерлих считал первоначально, что соответственные углы изоморфных кристаллов абсолютно тождественны. Волластон, однако, уже ранее показал, что ромбоэдрические углекислые шпаты, признанные Митчерлихом изоморфными, обладают близко похожими, но не … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
гомеоморфизм — гомеоморфизм, гомеоморфизмы, гомеоморфизма, гомеоморфизмов, гомеоморфизму, гомеоморфизмам, гомеоморфизм, гомеоморфизмы, гомеоморфизмом, гомеоморфизмами, гомеоморфизме, гомеоморфизмах (Источник: «Полная акцентуированная парадигма по А. А.… … Формы слов
ГОМЕОМОРФИЗМ — взаимно однозначное соответствие между двумя топологич. пространствами, при к ром оба взаимно обратных отображения, определяемые этим соответствием, непрерывны. Эти отображения наз. гомеоморфными, или топологическими, отображениями, а также… … Математическая энциклопедия
гомеоморфизм — гомеоморф изм, а … Русский орфографический словарь
Гомеоморфизм
Гомеоморфи́зм (греч. ομοιο — похожий, μορφη — форма) — это взаимно-однозначное и непрерывное отображение, обратное к которому тоже непрерывно. Иными словами, это биекция, связывающая топологические структуры двух пространств (в силу непрерывности биекции, образы и прообразы отображения являются открытыми множествами, определяющими топологии соответствующих пространств).
Пространства, связанные гомеоморфизмом, топологически неразличимы.
Содержание
Определение
Пусть 




Пространства 

Теорема о гомеоморфизме
Пусть 



Пример
Произвольный открытый интервал 


См. также
Литература
Полезное
Смотреть что такое «Гомеоморфизм» в других словарях:
гомеоморфизм — гомеоморфизм … Орфографический словарь-справочник
гомеоморфизм — сущ., кол во синонимов: 1 • гомеоморфность (1) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
гомеоморфизм — Морфологическое и иное сходство различных организмов, не связанных между собой непосредственным родством, обусловленное обитанием в сходных условиях; Г. является одним из проявлений конвергенции. [Арефьев В.А., Лисовенко Л.А. Англо русский… … Справочник технического переводчика
Гомеоморфизм — (от Гомео. и греч. morphe вид, форма) одно из основных понятий топологии. Две фигуры (точнее, два топологических пространства) называются гомеоморфными, если существует взаимно однозначное непрерывное отображение любой из них на другую … Большая советская энциклопедия
Гомеоморфизм — Митчерлих считал первоначально, что соответственные углы изоморфных кристаллов абсолютно тождественны. Волластон, однако, уже ранее показал, что ромбоэдрические углекислые шпаты, признанные Митчерлихом изоморфными, обладают близко похожими, но не … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
гомеоморфизм — гомеоморфизм, гомеоморфизмы, гомеоморфизма, гомеоморфизмов, гомеоморфизму, гомеоморфизмам, гомеоморфизм, гомеоморфизмы, гомеоморфизмом, гомеоморфизмами, гомеоморфизме, гомеоморфизмах (Источник: «Полная акцентуированная парадигма по А. А.… … Формы слов
ГОМЕОМОРФИЗМ — взаимно однозначное соответствие между двумя топологич. пространствами, при к ром оба взаимно обратных отображения, определяемые этим соответствием, непрерывны. Эти отображения наз. гомеоморфными, или топологическими, отображениями, а также… … Математическая энциклопедия
гомеоморфизм — гомеоморф изм, а … Русский орфографический словарь
ГОМЕОМОРФИЗМ
— взаимно однозначное соответствие между двумя топологич. пространствами, при к-ром оба взаимно обратных отображения, определяемые этим соответствием, непрерывны. Эти отображения наз. гомеоморфными, или топологическими, отображениями, а также гомеоморфизмами, а о пространствах говорят, что они принадлежат одному топологическому типун наз. гомеоморфными, или топологически эквивалентными. Они являются изоморфными объектами в категории топологич. пространств и непрерывных отображений. Следует отличать Г. от уплотнения (в к-ром непрерывность обязательна только в одну сторону); однако уплотнение бикомпакта на хаусдорфово пространство является Г.
Примеры. 1) Функция 
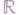
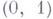
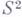
Термин «Г.» был введен А. Пуанкаре (Н. Poincare) в 1895 (см. [3]) в применении к (кусочно) дифференцируемым отображениям областей и подмногообразий пространства 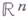
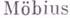

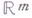

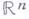
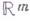
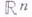



Другая проблема состоит в топологической характер и заци и отдельных пространств и классов пространств (т. е. их указания характеристических топологич. свойств, формулируемых на языке аксиом топологии). Она решена, напр., для одномерных многобразий, двумерных многообразий, канторова множества, кривой Серпинского, кривой Менгера, псевдодуги, пространства Бэра и др. Универсальный метод для топологич. характеризации пространств дают спектры. С их помощью получена теорема Александрова о Г. (см. [4]). Последовательностью измельчающихся подразделений охарактеризована сфера и вообще класс локально евклидовых пространств (см. [5]). Посредством спектров дано описание локально бикомпактных групп (см. [6]). Другой метод состоит в рассмотрении различных алгебраич. структур, связанных с отображениями. Так, бикомпактное пространство совпадает с пространством максимальных идеалов алгебры действительных функций, заданных на нем.
Многие пространства характеризуются полугруппой непрерывных отображений в себя (см. Гомеоморфизмов группа). В общей топологии дается топологич. описание многих классов топологич. пространств. Представляет интерес также характеризация пространств внутри данного класса. Напр., очень полезно описание сферы как компактного многообразия, покрытого двумя открытыми клетками. Мало разработан вопрос об алгоритмич. распознавании пространств. Напр., он не решен (к 1977) для сферы 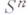
Еслп два пространства гомеоморфны, то для установления Г. общее значение имеет лишь метод спектров (и измельчающихся подразделений). С другой стороны, в том случае, когда построена классификация, вопрос решается сравнением инвариантов. На практике установление Г. часто оказывается очень трудной геометрич. задачей, к-рую приходится решать специальными средствами. Так, Г. евклидова пространства и нек-рых его факторпространств устанавливается с помощью псевдоизотопии.
ГОМЕОМОРФИЗМ
— взаимно однозначное соответствие между двумя топологич. пространствами, при к-ром оба взаимно обратных отображения, определяемые этим соответствием, непрерывны. Эти отображения наз. гомеоморфными, или топологическими, отображениями, а также гомеоморфизмами, а о пространствах говорят, что они принадлежат одному топологическому типун наз. гомеоморфными, или топологически эквивалентными. Они являются изоморфными объектами в категории топологич. пространств и непрерывных отображений. Следует отличать Г. от уплотнения (в к-ром непрерывность обязательна только в одну сторону); однако уплотнение бикомпакта на хаусдорфово пространство является Г.
Примеры. 1) Функция устанавливает Г. между числовой прямой и интервалом ; 2) замкнутый круг гомеоморфен любому замкнутому выпуклому многоугольнику; 3) трехмерное проективное пространство гомеоморфно группе вращений пространства R 3 вокруг начала и также пространству единичных касательных векторов к сфере ; 4) все бикомпактные нульмерные группы со счетной базой гомеоморфны канторову множеству; 5) бесконечномерные и сепарабельные банаховы пространства и даже пространства Фреше гомеоморфны между собой; 6) сфера и тор негомеоморфны.
Другая проблема состоит в топологической характер и заци и отдельных пространств и классов пространств (т. е. их указания характеристических топологич. свойств, формулируемых на языке аксиом топологии). Она решена, напр., для одномерных многобразий, двумерных многообразий, канторова множества, кривой Серпинского, кривой Менгера, псевдодуги, пространства Бэра и др. Универсальный метод для топологич. характеризации пространств дают спектры. С их помощью получена теорема Александрова о Г. (см. [4]). Последовательностью измельчающихся подразделений охарактеризована сфера и вообще класс локально евклидовых пространств (см. [5]). Посредством спектров дано описание локально бикомпактных групп (см. [6]). Другой метод состоит в рассмотрении различных алгебраич. структур, связанных с отображениями. Так, бикомпактное пространство совпадает с пространством максимальных идеалов алгебры действительных функций, заданных на нем.
Многие пространства характеризуются полугруппой непрерывных отображений в себя (см. Гомеоморфизмов группа). В общей топологии дается топологич. описание многих классов топологич. пространств. Представляет интерес также характеризация пространств внутри данного класса. Напр., очень полезно описание сферы как компактного многообразия, покрытого двумя открытыми клетками. Мало разработан вопрос об алгоритмич. распознавании пространств. Напр., он не решен (к 1977) для сферы при
Еслп два пространства гомеоморфны, то для установления Г. общее значение имеет лишь метод спектров (и измельчающихся подразделений). С другой стороны, в том случае, когда построена классификация, вопрос решается сравнением инвариантов. На практике установление Г. часто оказывается очень трудной геометрич. задачей, к-рую приходится решать специальными средствами. Так, Г. евклидова пространства и нек-рых его факторпространств устанавливается с помощью псевдоизотопии.
Гомеоморфно что это значит
Равносильное определение: непрерывным называется отображение, при котором прообразы замкнутых множеств замкнуты.
Упражнение. Проверьте эквивалентность двух определений непрерывного отображения.
Также нам потребуется определение отображения, непрерывного в точке.
Числовая прямая является метрическим пространством с метрикой вида поэтому, выбрав окрестности точек в виде открытых шаров (которые в данном случае являются открытыми интервалами), получим определение функции, непрерывной в точке.
Можно доказать, что отображение топологических пространств непрерывно тогда и только тогда, когда оно непрерывно в каждой точке.
Теперь обратимся к простейшим свойствам непрерывных отображений топологических пространств.
Теорема 1. Тождественное отображение топологического пространства в себя непрерывно.
Теорема 3. Отображение вложения подпространства в топологическое пространство непрерывно.
Теорема 4. Композиция непрерывных отображений топологических пространств непрерывна.
Для доказательства рассмотрим непрерывные отображения топологических пространств и и их композицию
Теперь обратимся к понятию категории.
Для любого неодноточечного пространства постоянное отображение не является гомеоморфизмом (оно не взаимно однозначно и тем более не обратимо).
Приведем примеры гомеоморфных топологических пространств, известных из других курсов геометрии.
Обратное отображение плоскости на параболоид имеет вид:
Оба отображения заданы непрерывными функциями и, следовательно, непрерывны, что и доказывает гомеоморфизм.
2. Трехосный эллипсоид гомеоморфен сфере.
Каноническое уравнение трехосного эллипсоида имеет вид:
Уравнение сферы с центром в начале координат: Отображение эллипсоида на сферу, осуществляющее гомеоморфизм, задается в координатах следующим образом:
Аналогично, в силу непрерывности обратного отображения прообраз при отображении любого открытого в множества также открыт:
Доказанное означает, что если некоторое топологическое утверждение верно для одного из двух гомеоморфных топологических пространств, то такое же утверждение верно для другого. Гомеоморфные пространства топологически неразличимы, поэтому о них говорят, что они имеют один топологический тип.
Отношение гомеоморфности в классе топологических пространств рефлексивно, симметрично и транзитивно, то есть является отношением эквивалентности (докажите!)
Топологические пространства могут быть негомеоморфными, но локально гомеоморфными. Таковы, например, тор (компактное пространство) и евклидова плоскость (некомпактное пространство.)




