Граф что это в информатике это

Неориентированный граф

В математической теории графов и информатике граф — это совокупность объектов со связями между ними.

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — это связи, созданные гиперссылками (см. Тематическая карта).

Содержание

Определения

Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Приводимые ниже определения — наиболее часто встречаемые.

V (а значит и E ) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становятся ложными в случае бесконечных множеств.

Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.

Два ребра называются смежными, если они имеют общую концевую вершину.

Два ребра называются кратными, если множества их концевых вершин совпадают.

Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Ориентированный граф

Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v 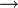w ведёт от вершины v к вершине w.

Смешанный граф

Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.

Прочие связанные определения

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Ориентированным путём в орграфе называют конечную последовательность вершин v_i 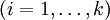, для которой все пары (v_i,v_{i + 1}) являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:

Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v », является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.

Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов

Ребро графа называется мостом, если его удаление увеличивает число компонент.

Дополнительные характеристики графов

Способы представления графа в информатике

Матрица смежности

Матрица смежности — таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).

Недостатком являются требования к памяти — очевидно, квадрат количества вершин.

Матрица инцидентности

Данный способ является самым ёмким (размер пропорционален | E | | V | ) и неудобным для хранения, но облегчает нахождение циклов в графе.

Список рёбер

Список рёбер — это тип представления графа в памяти, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.

Обобщение понятия графа

Простой граф является одномерным симплициальным комплексом.

Более абстрактно, граф можно задать как тройку , где V и E — некоторые множества (вершин и рёбер, соотв.), а — функция инцидентности (или инцидентор), сопоставляющая каждому ребру (упорядоченную или неупорядоченную) пару вершин u и v из V (его концов). Частными случаями этого понятия являются:

Под данное выше определение не подходят некоторые другие обобщения:

Литература

См. также

Ссылки

Популярные программы для визуализации графов

Источник

Информатика. 9 класс

На прошлом уроке мы уже говорили о том, что одним из методов познания является моделирование, рассматривали различные классификации моделей и выделили в качестве предмета нашего рассмотрения информационные модели. Среди них можно выделить графические информационные модели, к которым относятся карты, чертежи, схемы, диаграммы, графики и предмет сегодняшнего рассмотрения — графы.

Если рассматривать группу объектов вместе с имеющимися между ними связями как единое целое, то можно говорить о системе. Мы можем графически изобразить объекты системы вершинами, а связи между ними линиями (рёбрами). В этом случае мы получим информационную модель системы в форме графа.

Если рёбра графа имеют направление, то оно отображается стрелками, а граф называется ориентированным (направленным).

Вершины графа могут отображаться точками, кругами, прямоугольниками и т.д.

Если вершины или ребра графа характеризуются некоторой дополнительной информацией — весом вершины или ребра, то такой граф называют взвешенным.

С помощью взвешенных графов удобно изображать дороги между населенными пунктами. Например, в приведенном примере указана протяжённость дорог в километрах.

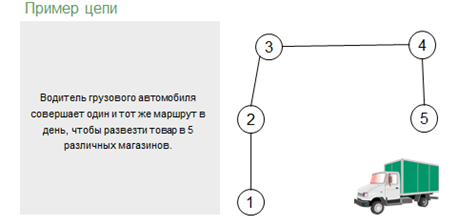
Проведём путь, проходящий по вершинам и ребрам графа так, чтобы любое ребро входило в него не более одного раза. Такой путь называется цепью. Цепь, у которой совпадают начальная и конечная вершины, называется циклом.

Граф с циклом называется сетью . Если персонажей некоторого литературного произведения, мультфильма или сериала представить вершинами графа, а связи между ними изобразить рёбрами, то получится граф, который называют семантической сетью.

Информационные модели в виде графов широко используются в повседневной жизни.

Например, при проектировании нового жилого района можно здания обозначить как вершины графа, а дороги, коммуникации и т.д. — ребрами графа. По таким графам удобно, например, прогнозировать загрузку дорог и находить оптимальные транспортные маршруты. Другим примером является схема метрополитена. Вершинами в графе в этом случае являются станции метро.

Граф, в котором отсутствуют циклы, называется деревом.

В этом случае между любыми двумя вершинами существует только один путь.

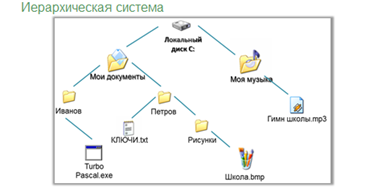
С помощью дерева удобно представлять иерархическую систему.

У дерева выделяется одна главная вершина, которую называют корнем.

Каждая вершина дерева, исключая корень, может иметь только одного предка (вершина верхнего уровня), но при этом может порождать множество потомков, отображаемых вершинами нижнего уровня. Вершины, у которых отсутствуют порожденные вершины, называются листьями.

Одним из известных применений графов является генеалогическое или родословное дерево, на котором отображаются родственные связи.

Существуют задачи, которые удобно решать с помощью графов.

Например, если мы хотим отобразить все возможные варианты трехзначных чисел, которые могут получиться из цифр 7 и 8.

С помощью графов удобно решать задачи на определение выигрышной стратегии игроков.

Задача на анализ информации, представленной в виде графа, является одной из предлагаемых на государственной итоговой аттестации по информатике.

Итак, сегодня вы узнали о том, какие бывают графы и из каких элементов они состоят, для каких целей создаются. Получили представление об ориентированных и неориентированных графах, деревьях. Научились решать задачи на определение количества путей в графе, используемые при государственной итоговой аттестации. Закрепите полученные знания на практике, выполнив упражнения.

Вводятся понятия — Граф. Вершина, ребро, путь. Ориентированные и неориентированные графы. Длина (вес) ребра и пути. Дерево. Корень, лист, вершина.

1. Обсуждение различных графических информационных моделей. На этом этапе происходит коллективное обсуждение существующих технологических решений для создания графических информационных моделей;

2. Определяется необходимость рассмотрения группы объектов вместе с существующими между ними связями, т.е. системы. Затем — возможность получения информационной модели системы в форме графа. Рассматриваются различные варианты отображения графов;

3. Определение понятий — Граф. Вершина, ребро, путь. Ориентированные и неориентированные графы. Длина (вес) ребра и пути. Дерево. Корень, лист, вершина.

4. Исследование различных возможных путей, проходящих по вершинам и ребрам графа. Цепь. Цикл.

5. Реализация интерактивного элемента с целью проверки первичного усвоения нового материала;

6. Определение сети. Исследование возможных вариантов применения информационных моделей в форме графов в повседневной жизни;

7. Определение Дерева. Корень, Предки, Потомки, Листья. Исследование возможностей, предоставляемых различными сервисами для построения генеалогического дерева;

8. Использование графов для графического представления решения различных задач. Задача о построении дерева возможных трёхзначных чисел.

Разбор задачи демонстрационного варианта ФИПИ-2017 на анализ информации, представленной в виде схем

Источник

Граф что это в информатике это

Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер.

Классификация графов

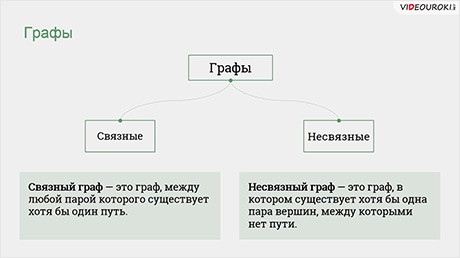
В связном графе между любой парой вершин существует как минимум один путь.

В несвязном графе существует хотя бы одна вершина, не связанная с другими.

Графы также подразделяются на

В ориентированном графе ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами.

В неориентированном графе по каждому из ребер можно осуществлять переход в обоих направлениях.

Частный случай двух этих видов – смешанный граф. Он характерен наличием как ориентированных, так и неориентированных ребер.

Способы представления графа

Граф может быть представлен (сохранен) несколькими способами:

Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Размер массива зависит от количества вершин и/или ребер в конкретном графе.

Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1.
Число строк матрицы смежности равно числу столбцов и соответствует количеству вершин графа.

Когда из одной вершины в другую проход свободен (имеется ребро), в ячейку заносится 1, иначе – 0. Все элементы на главной диагонали равны 0 если граф не имеет петель.

Матрица инцидентности (инциденции) графа — это матрица, количество строк в которой соответствует числу вершин, а количество столбцов – числу рёбер. В ней указываются связи между инцидентными элементами графа (ребро(дуга) и вершина).

В неориентированном графе если вершина инцидентна ребру то соответствующий элемент равен 1, в противном случае элемент равен 0.

Матрица инцидентности для своего представления требует нумерации рёбер, что не всегда удобно.

Список смежности (инцидентности)
Если количество ребер графа по сравнению с количеством вершин невелико, то значения большинства элементов матрицы смежности будут равны 0. При этом использование данного метода нецелесообразно. Для подобных графов имеются более оптимальные способы их представления.

По отношению к памяти списки смежности менее требовательны, чем матрицы смежности. Такой список можно представить в виде таблицы, столбцов в которой – 2, а строк — не больше, чем вершин в графе.
В каждой строке в первом столбце указана вершина выхода, а во втором столбце – список вершин, в которые входят ребра из текущей вершины.

Преимущества списка смежности:

Недостатки списка смежности:

Алгоритмы обхода графов

Основными алгоритмами обхода графов являются

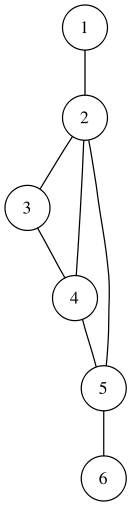
Поиск в ширину подразумевает поуровневое исследование графа:

Вершины просматриваются в порядке возрастания их расстояния от корня.
Алгоритм прекращает свою работу после обхода всех вершин графа, либо в случае выполнения требуемого условия (например, найти кратчайший путь из вершины 1 в вершину 6).
Каждая вершина может находиться в одном из 3 состояний:

Фиолетовый – рассматриваемая вершина.

Применения алгоритма поиска в ширину

Алгоритм поиска в ширину работает как на ориентированных, так и на неориентированных графах.
Для реализации алгоритма удобно использовать очередь.

Реализация на C++ (с использованием очереди STL)

Результат выполнения

Задача поиска кратчайшего пути
Реализация на С++

Поиск в глубину – это алгоритм обхода вершин графа.

Поиск в ширину производится симметрично (вершины графа просматривались по уровням). Поиск в глубину предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность продвижения означает, что следующим шагом будет переход на последний, имеющий несколько вариантов движения (один из которых исследован полностью), ранее посещенный узел (вершина).

Отсутствие последнего свидетельствует об одной из двух возможных ситуаций:

Каждая вершина может находиться в одном из 3 состояний:

Фиолетовый – рассматриваемая вершина.

Применения алгоритма поиска в глубину

Алгоритм поиска в глубину работает как на ориентированных, так и на неориентированных графах. Применимость алгоритма зависит от конкретной задачи.
Для реализации алгоритма удобно использовать стек или рекурсию.

Реализация на C++ (с использованием стека STL)

Результат выполнения

Задача поиска лексикографически первого пути на графе.
Реализация на C++

Результат выполнения

Поиск в глубину также может быть реализован с использованием рекурсивного алгоритма.

Реализация обхода графа в глубину на C++ (с использованием рекурсии)

Источник

Структурные модели систем. Графы

Урок 3. Информатика 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Структурные модели систем. Графы»

Вспомним ключевые термины прошлого урока.

Системный анализ – это исследование реальных объектов и явлений с точки зрения системного подхода, состоящее из этапов анализа и синтеза.

Модель «чёрного ящика» – это указание входов и выходов системы, а также зависимости между ними.

Модель состава – это своеобразный список элементов системы.

На данном уроке мы с вами узнаем, что такое структурная модель системы, что используется для её отображения, а также вспомним, из чего состоят графы.

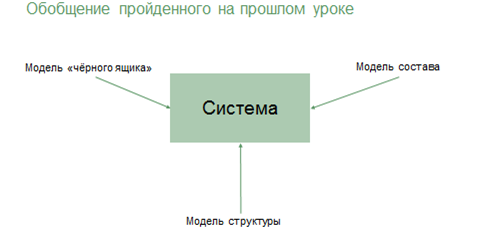
Если обобщить всё пройдённое на прошлом уроке, можно сказать, что модель «чёрного ящика», модель состава и модель структуры полностью описывают систему и образуют ещё одну модель, которая называется структурной моделью системы или структурной схемой. На структурной схеме отражается состав системы и её внутренние связи. Для отображения структурной схемы системы используются графы.

Граф – это совокупность объектов со связями между ними.

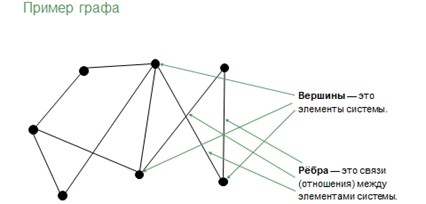
Графически это будет выглядеть следующим образом: вершины (точки) – это элементы системы, а ребра (линии между ними) – это связи (отношения) между элементами системы.

Примером графа является схема движения автобусов в городе, где вершины – это остановки, а рёбра – это пути передвижения автобусов. С помощью такой схемы проще определить на каком автобусе нужно доехать с одной остановки до другой.

Графы бывают ориентированными и неориентированными.

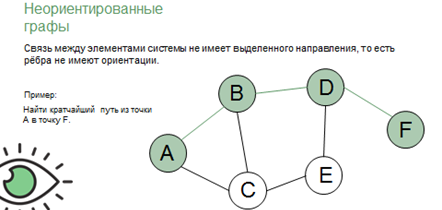
В неориентированных графах связь между элементами системы не имеет выделенного направления, то есть рёбра не имеют ориентации. Примером неориентированного графа будет являться решение задачи на нахождение кратчайшего пути. Граф для решения одной из таких задач, условием которой является нахождение кратчайшего пути из точки A в точку F, будет выглядеть следующим образом.

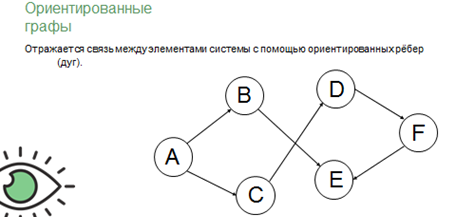
В ориентированных графах наоборот отражается связь между элементами системы с помощью ориентированных рёбер (стрелок). Такие рёбра называются дугами.

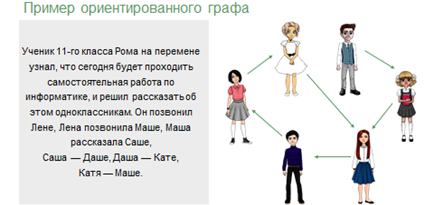
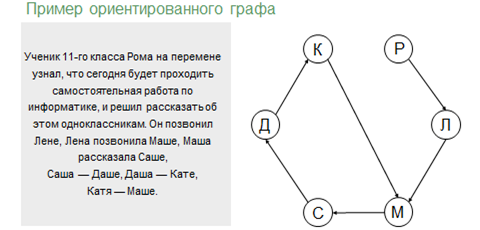
Так же с помощью дуг указывается не только наличие связи, но и какой из двух элементов является «началом» связи, а какой «концом». К примеру ориентированного графа можно отнести графическое изображение следующего условия: ученик 11 класса Рома на перемене узнал, что сегодня будет проходить самостоятельная работа по информатике, и решил рассказать об это одноклассникам. Он позвонил Лене, Лена позвонила Маше, Маша рассказала Саше, Саша – Даше, Даша – Кате, Катя – Маше.

Изобразим каждого учащегося как вершины графа, название которых будут отмечены первыми буквами имён, а звонки или разговоры дугами. Начало дуги будет находиться у вершины учащегося, который рассказывал про самостоятельную, а конец – у вершины того, кому рассказывали. Таким образом, мы получим ориентированный граф.

В ориентированном графе связями между вершинами будут дуги, а в неориентированном – рёбра.

Ещё графы бывают взвешенными. Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.

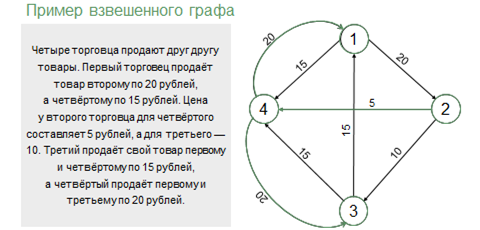
Нарисуем взвешенный граф на основе следующего условия: четыре торговца продают друг другу товары. Первый торговец продаёт товар второму по 20 рублей, а четвёртому по 15 рублей. Цена товара у второго торговца для четвёртого составляет 5 рублей, а для третьего – десять. Третий продаёт свой товар первому и четвёртому по 15 рублей, а четвёртый продаёт первому и третьему по 20 рублей. Для обозначения рыночных отношений между торговцами будем использовать дуги, а для указания веса, будем писать его над каждой дугой.

Для начала рисуем все вершины и обозначим их цифрами от одного до четырёх. Затем, по условию задачи первый торговец продаёт свой товар второму и четвёртому. Проведём стрелку от первого ко второму и от первого к четвёртому. Затем над каждой из них запишем соответствующую цену. Таким же образом оформляем весь граф. С помощью данного графа мы можем увидеть, что, например, для четвёртого торговца выгоднее продать товар первому и третьему, а купить у второго. И так далее.

Так же графы бывают связными и несвязными.

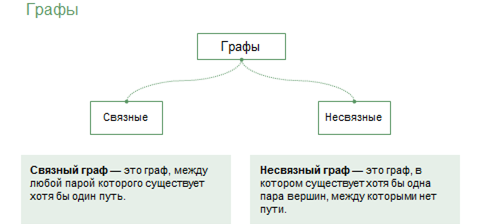
Связный граф – это граф, между любой парой которого существует хотя бы один путь.

Примерами связных графов являются все вышерассмотренные графы.

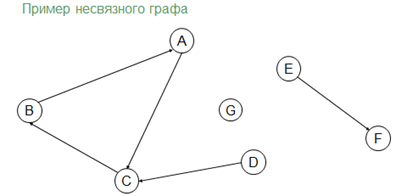
Несвязный граф – это граф, в котором существует хотя бы одна пара вершин, между которыми нет пути. Такие вершины называются несвязными. Например, на показанном графе несвязными вершинами является G и любая другая вершина данного графа.

Следующее понятие, с которым мы должны познакомиться: цепь. Итак, цепь – это путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза. То есть, при построении пути, по одному и тому же ребру можно пройти только один раз.

Например, водитель грузового автомобиля совершает один и тот же маршрут в день, чтобы развезти товар в пять различных магазинов. Давайте построим с помощью графа путь водителя. Обозначим вершинами все пять магазинов, и пронумеруем их от одного до пяти. Далее, водитель заехал в первый магазин, выгрузил необходимый товар и поехал во второй магазин. Изобразим ребром путь от первого магазина ко второму. Затем поехал в третий, четвёртый и пятый. Также изобразим данные пути с помощью рёбер. Обратите внимание, что водитель проезжает по каждому ребру только один раз. Данный граф будет являться примером цепи.

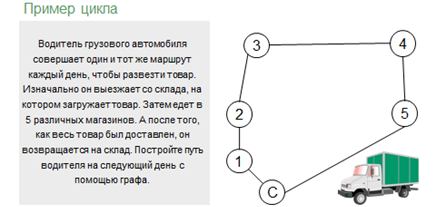
Цикл – это цепь, в которой начальная и конечная вершины совпадают.

Разберём пример, похожий на предыдущий, но с некоторыми изменениями. Водитель грузового автомобиля совершает один и тот же маршрут каждый день, чтобы развезти товар. Изначально он выезжает со склада, на котором загружает товар. Затем едет в пять различных магазинов. А после того, как весь товар был доставлен, он возвращается на склад. Давайте снова построим путь водителя на следующий день с помощью графа. Обозначим вершинами склад и все пять магазинов, где цифры от одного до пяти будут обозначать магазины, а склад обозначим буквой «С». Изначально водитель заезжает на склад, затем едет в первый магазин, чтобы выгрузить необходимый товар. Обозначим этот путь ребром. Далее он едет из первого магазина во второй. Также изобразим ребром этот путь. Затем водитель едет в третий, четвёртый и пятый магазины. Снова изобразим данные пути с помощью рёбер. Из пятого магазина он едет на склад. Отметим этот путь на нашем графе. Обратите внимание, что водитель проезжает по каждому ребру только один раз и в конце возвращается в первоначальную вершину – на склад. Данный граф будет являться примером цикла.

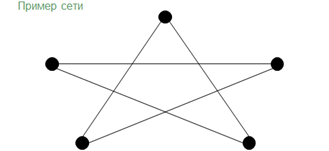
Сеть – это граф с циклом.

В качестве примера сюда можно отнести пятиконечную звезду, но прежде чем проводить ребра, обозначим точкой каждую из вершин. Затем начиная с нижней соединим их.

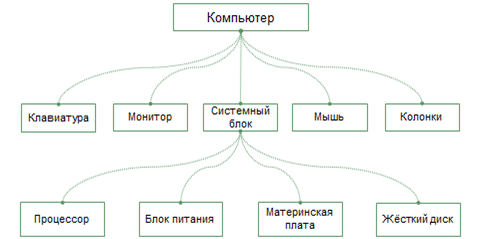
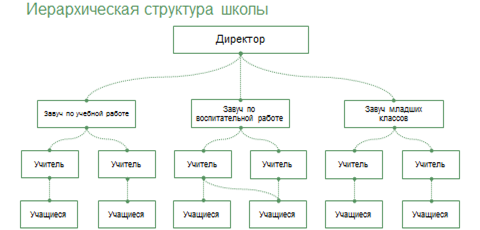
На практике часто приходится строить системы с иерархической системой. Такой граф называется деревом.

Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину. Отличительная особенность дерева: между любыми двумя его вершинами существует единственный путь.

Корень дерева – это единственная главная его вершина.

Каждая вершина дерева (кроме корня) имеет только одного предка. Обозначенный предком объект входит в один класс высшего уровня. Любая вершина дерева может порождать несколько потомков.

Потомки – это вершины, которые соответствуют классам нижнего уровня. Такой принцип связи называется «один-ко-многим».

Листья – это вершины, которые не имеют потомков.

Разберёмся более подробно на примере.

Давайте построим иерархическую структуру школы. Во главе будет находиться директор и соответственно он будет корневой вершиной нашего дерева. Далее на втором уровне будут находиться завуч по учебной работе, завуч по воспитательной работе, завуч младших классов, далее учителя и учащиеся. В данной структуре мы можем видеть, что Потомками являются все, кроме директора, предками – все, кроме учащихся, а листьями – учащиеся, так как в данной структуре у них нет потомков.

· Структурная модель системы отражает состав и внутренние связи системы.

· Граф – это графическое отображение структурной модели; состоит из вершин и линий (рёбер и дуг).

· Дерево – это ориентированный граф системы с иерархической структурой; связь – «один ко многим».

Источник