Граф имеет 4 ребра чему равна сумма степеней вершин в этом графе
Степень вершины (теория графов)
Содержание
Лемма о рукопожатиях
По формуле суммы степеней для графа 
то есть сумма степеней вершин любого графа равна удвоенному числу его рёбер. Кроме того, формула утверждает, что в любом графе число вершин нечётной степени чётно. Данное утверждение (и сама формула) известны как лемма о рукопожатиях. Название происходит от известной математической задачи: необходимо доказать, что в любой группе число людей, пожавших руку нечётному числу других чётно.
Последовательность степеней вершин
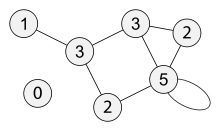
Последовательность степеней вершин неориентированного графа является невозрастающей последовательностью. [2] Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа, поэтому у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристкой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.
Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической (англ. graphical sequence ). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа. Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары, к оставшимся незаполненными вершинам следует добавить петли.
Сложнее реализовать простой граф с заданной последовательностью. Теорема Эрдёша — Галлаи утверждает, что невозрастающая последовательность di (при i = 1,…,n) может быть последовательностью простого графа только если её сумма чётна и выполняется неравенство
Например, последовательность (3, 3, 3, 1) не может являться последовательностью простого графа; она удовлетворяет неравенству Эрдёша — Галлаи только при k равном 1, 2 или 4, но не при k равном 3.
С. Л. Хакими доказал, что (d1, d2, …, dn) есть последовательность степеней простого графа только если существует (d2 − 1, d3 − 1, …, dd1+1 − 1, dd1+2, dd1+3, …, dn). Этот факт позволил разработать простой алгоритм нахождения простого графа с заданной реализуемой последовательностью:
Проблема нахождения или оценки числа графов по заданной последовательности относится к области перечисления графов.
Частные значения
Общие свойства
См. также
Примечания
Источники
Полезное
Смотреть что такое «Степень вершины (теория графов)» в других словарях:
Дуга (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Цикл (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Дерево (теория графов) — У этого термина существуют и другие значения, см. Дерево (значения). Дерево это связный ациклический граф.[1] Связность означает наличие путей между любой парой вершин, ацикличность отсутствие циклов и то, что между парами вершин… … Википедия
Графов теория — раздел конечной математики (См. Конечная математика), особенностью которого является геометрический подход к изучению объектов. Основное понятие теории граф. Граф задаётся множеством вершин (точек) и множеством рёбер (связей), соединяющих … Большая советская энциклопедия
Глоссарий теории графов — Эта страница глоссарий. См. также основную статью: Теория графов Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице) … Википедия
Словарь терминов теории графов — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия
Практическое применение раскраски графов — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Раскраска графов практически применяется (постановку задачи различиных раскрасок здесь обсуждаться не будет) дл … Википедия
Теоремы теории графов — Здесь собраны теоремы из теории графов. Содержание 1 Лемма о рукопожатиях 2 Существование эйлерова пути и цикла … Википедия
Вершина (граф) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Длина пути в орграфе — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Содержание урока
Матрица смежности графа
Матрица смежности графа
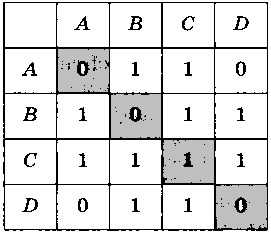
Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).
Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).
Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?
В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.
Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).
Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?
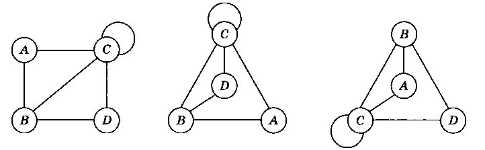
Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).
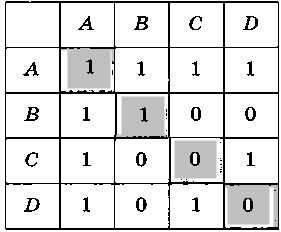
Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.
Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?
Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?
Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?
Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?
Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?
Следующая страница 
Cкачать материалы урока
Сумма степеней всех вершин в графе равна удвоенному количеству ребер в нем!
Графы!
Вводное.
Суть вы поняли! Кстати, карта метро – уже готовый граф.
Основные понятия, которые нам нужны.
Вершины графа – это те самые точки, которые мы соединяем. Города, числа, люди и так далее.
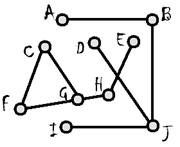
Степень вершины – число ребер, выходящих из нее. Например, в графе, который нарисован справа, вершины A, I, E и D имеют степень 1, потому что из них выходит всего по одному ребру, вершины B, H, F и С имеют степень 2, а вершины G и J имеют степень 3.
Если в графе всего N вершин, то максимальная степень вершины в нем может быть равна N-1 – когда одна вершина соединена со всеми остальными. Минимальная, разумеется, может быть равна 0.
Путь в графе – последовательность вершин, в которой любые две соседние вершины соединены между собой ребром. На данной картинке, например, A B J I – путь.
Цикл в графе – путь, у которого первая вершина совпадает с последней. На картинке – C G F C.
Связный граф – граф, в котором от любой до любой другой существует путь (то есть можно «дойти» по ребрам). Например, граф справа не связный, ведь от A до E, например, не добраться.
1) Нарисуйте граф с 6 вершинами и степенями вершин 2,2,3,3,4,4
2) Попробуйте нарисовать граф с 7 вершинами и степенями 6,6,4,4,2,1,1. Почему не получается?
Основное соображение.
Но! Поскольку каждое ребро выходит ровно из двух вершин, мы и учли его дважды. Например, ребро между А и Б мы подсчитали и в степени А, и в степени Б. Следовательно, наше полученное число следует еще разделить пополам, и тогда мы получим реальное количество ребер. То есть
Сумма степеней всех вершин в графе равна удвоенному количеству ребер в нем!
Приятное следствие: сумма степеней вершин графа всегда четна. Потому что она равна удвоенному числу ребер. И этим тоже следует активно пользоваться.
Примеры того, как помогают решать задачи эти соображения.
Пример №1: Могут ли все вершины в графе иметь степень 2, а одна вершина – степень 3?
Ответ: Нет, не могут. Сумма степеней – какое-то количество двоек и одна тройка – безусловно нечетна. А она не может быть нечетной, потому что равна удвоенному количеству ребер.
Пример №2: В графе сто вершин и а) каждая соединена с каждой; б) у каждой степень равна 50; в) степень 25 из них равна 4, 25 – 8, а у 50 – 6. Сколько ребер в графе?
Решите это сами:
3) Известно, что в графе все степени вершин равны, самих вершин 24, а ребер – 60. Чему равна степень любой вершины этого графа?
4) Докажите, что в любом графе какие-то две вершины имеют одинаковую степень.
5*) В компании из k человек каждый имеет ровно трех знакомых, любые двое незнакомых имеют общего знакомого и есть трое попарно знакомых. Найдите наибольшее возможное значение k.
6) В стране есть несколько аэропортов, каждый из которых соединён авиалиниями ровно с пятью другими. Однажды из-за сильного снегопада бóльшую часть аэропортов пришлось закрыть. После этого оказалось, что из каждого работающего аэропорта можно вылететь только в три других, а закрытыми оказались 26 авиалиний. (Авиалиния закрывается, если закрывается хотя бы один из двух аэропортов, которые она соединяет.)
а) Докажите, что число работающих после снегопада аэропортов чётно.
б*) Докажите, что число закрывшихся аэропортов делится на 4.
в*) Сколько авиалиний не закрылось из-за снегопада?
Делимость и остатки.
С остатками все просто. Любое натуральное число от деления на любое другое дает какой-то остаток (иногда этот остаток равен 0, и тогда мы говорим, что одно число делится на другое). Например, 10 дает остаток 1 от деления на 3 и остаток 2 от деления на 8. И, к слову, оно же дает остаток 10 от деления на 11, 25, 26, 100, 413… и так далее. В общем, на любое число, которое больше, чем оно само.
«Степень вершины и подсчет числа ребер графа». 7-й класс
Класс: 7
Презентация к уроку
Профиль класса: общеобразовательный.
Тип урока: изучение и первичное закрепление новых знаний.
Давайте вспомним основные понятия теории графов. Для этого проведем разминку по типу незаконченного предложения (Презентация, сл.: 2, 3, 4). Каждый ученик имеет карточки с пропущенными словами в предложение. Учитель зачитывает предложение, останавливаясь перед пропущенным словом, и выбирает ученика, который в свою очередь должен поднять карточку. Далее этот ученик читает дальше предложение, также останавливаясь перед пропущенным словом, и уже сам выбирает одноклассника для ответа и т. д. по цепочке.
Проверим в классе решение домашней задачи (Презентация, сл.: 5, 6, 7). Один ученик выходит к доске и рисует граф. Далее мы вместе проверяем ребра (дороги между городами), считаем количество выходящих ребер из каждой вершины и смотрим связи между городами.
Сегодня на уроке мы продолжим изучение графов, познакомимся с понятием “степень вершины графа” и сформулируем определение связности графа (обратим внимание на наш граф из домашнего задания и определим, является ли он связным или нет и почему). Рассмотрим утверждение о количестве ребер графа, и проверим в соответствие с этим утверждением, правильно ли мы посчитали количество ребер графа в домашней задаче. И рассмотрим теорему о четности числа нечетных вершин графа.
Количество ребер, выходящих из одной вершины, называют степенью этой вершины. Для петли будем считать, что это ребро выходит из вершины дважды (Презентация, сл. 8).
Запишем определение в рабочую тетрадь и зарисуем представленный граф, для данного графа посчитаем степень каждой вершины. Ребята смотрят на слайд и работают самостоятельно, далее вслух зачитаем степень каждой вершины.
Вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной (Презентация, сл. 9).
Запишем определение в тетрадь и перечислим через запятую сначала четные вершины, а потом нечетные вершины для уже нарисованного графа. Проверим задание вслух.
Количество ребер графа равно половине суммы степеней его вершин. Пусть граф имеет n вершин, тогда число ребер равно:
Запишем утверждение в рабочую тетрадь и посчитаем количество ребер графа в домашней задачке. Проверим ответ в классе. Рассмотрим задачу и ее решение на подсчет числа ребер графа без построения. (Презентация, сл. 11).
Сформулируем теорему о количестве вершин нечетной степени любого графа и запишем формулировку в рабочую тетрадь. (Презентация, сл. 12).
Теорема. Количество вершин нечетной степени любого графа всегда четно.
Доказательство: Количество ребер графа равно половине суммы степеней его вершин.
Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной.
А это возможно только в том случае, если граф содержит четное число нечетных вершин.
Разберем доказательство и проверим теорему на нашей домашней задачке.
Рассмотрим несколько задач.
Задача. В государстве 50 городов, из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
Решение. Подсчитаем общее количество выходящих дорог из городов: 50 * 4 = 200. Однако, мы понимаем, что при подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 100.
Задача. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей?
Ответ. Нет (теорема о четности числа нечетных вершин).
Сегодня мы с вами познакомились с новыми определениями, связанными с понятием графа, рассмотрели утверждение, которое помогает быстро подсчитывать число ребер графа, и сформулировали теорему, которая значительно упрощает решение многих задач. В частности, поучительная сторона этой теоремы заключается в исследовании и ответе на вопрос, возможно или нет решение данной задачи, прежде чем приступать за ее решение.
В качестве домашнего задания ученики получать карточки с тремя задачами (Презентация, сл. 13).
Граф имеет 4 ребра чему равна сумма степеней вершин в этом графе
Задачи
Построим граф, вершинами которого являются города, а ребрами — существующие авиалинии. Вспомним признак делимости на 3: натуральное число делится нацело на 3 тогда и только тогда, когда сумма его цифр делится на 3. Заметим, что если название города делится на 3, то он соединен авиалиниями только с городами, названия которых тоже делятся на 3. Наоборот, те города, названия которых не делятся на 3, не могут быть соединены авиалиниями с городами, названия которых делятся на 3. Поэтому города 3, 6 и 9 образуют одну компненту связности графа, в которую никакие другие города не входят. Это означает, что из города 1 в город 9 добраться по воздуху нельзя.
Упражнение: А какие еще компоненты связности есть в этом графе?
Теорема 1. Количество ребер в любом графе равно половине суммы степеней его вершин.
Докажите эту теорему самостоятельно по аналогии с задачей 5.
6. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?
Подсказка: попытайтесь посчитать количество телефонных проводов.
При решении всех последующих задач мы будем пользоваться этой теоремой. Любое решение следует начинать с выбора вершин и ребер графа. Попробуйте решить эти задачи самостоятельно, не ссылаясь на теорему, а заново проводя ее доказательство в каждом конкретном случае.
8. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 — по 4 друга, а 10 — по 5 друзей?