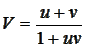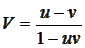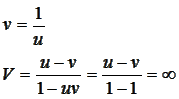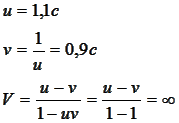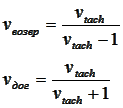Импульс тахиона что это
Коротко про тахионы
В общепринятой картине мира, в которой правит та самая Теория Относительности — «ТО», скорость света «С» считается предельной скоростью, и эту же величину приписывают предельной скорости взаимодействия, протекания всех процессов во вселенной. Та же ТО утверждает зависимость энергии и массы тела от скорости – знаменитое уравнение E=m*c2.
Т.е. для объекта, обладающего массой, и достигшего С, время попросту остановится, а масса и энергия станут бесконечными, что сами понимаете весьма нежелательно на практике как и любой парадокс).
Поэтому все частицы движущиеся со скоростью света, общее название «люксоны», среди них и фотоны, рассматриваются как частицы не имеющие массы покоя. Попросту говоря с нулевой массой, ведь на сколько нуль не умножай – нулем и останется, а значит и парадокса не произойдет. Ура!
Для частиц с досветовыми скоростями тоже нашли парочку замысловатых слов «тардио́ны» или «брадио́ны», и им даже разрешили иметь массу покоя, т.к. они световых скоростей не достигают, а значит правильных теорий не нарушают…
Но физики — ребята творческие, и стоит им что-то незыблемое постановить, как тут же возникает соблазн это опровергнуть. Что в принципе и понятно, потому что любая теория это вовсе не абсолютный закон, а лишь предположение, дополненное расчетами, и в различной степени подтверждаемое или опровергаемое опытным путем.
Однако, по каким то загадочным причинам, принято крайне щепетильно считаться с Теорией Относительности. И зачем то выверять соответствуют ли ей новые теории или данные полученные экспериментально… Не смотря на то, что это тоже всего лишь теория.
Поэтому когда в 1967 американский физик Джеральд Фейнберг рискнул удивить мир новой, сверхсветовой частицей, то он не стал лезть на рожон, и сразу математически доказал, что существование её вовсе не противоречит ТО!
И все остались довольны.
Назвал он этот класс частиц «тахионами».
Их скорость всегда быстрее света, но для этого им приходится иметь некую «мнимую» массу (что это значит, а главное – кто её «мнит», наверно, не скажет даже физик), и свойство терять скорость при поглощении энергии, тогда как все «нормальные» частицы ускоряются.
Все это конечно плачевно сказалось на тахионах, т.к. пришлось признать что их время течет вспять, и то что тахионы не могут доносить информацию, т.к. это к примеру, нарушило бы принцип причинности, и вообще не могут как либо взаимодействовать с частицами нашего мира, т.к. их скорость выше скорости взаимодействия в нашей вселенной. Они просто выпадают из нашей пространственно-временной и причинно-следственной структуры!
По этой причине, обнаружение и фиксация таких частиц представляются скорее всего невозможными… Пока не найдется новый сообразительный физик, конечно!
Чему равна скорость тахиона?
Относится к разделу Наука
Чему равна скорость тахиона?
Путенихин П.В.
m55@mail.ru
Если применить к сверхсветовому объекту преобразования Лоренца, неизбежно возникает противоречивая ситуация. Например, скорость тахиона в соответствии с этими преобразованиями становится зависимой от скорости ИСО, из которой за ним наблюдают, приводя во всех случаях к неизбежному «путешествию в прошлое». Никакое движение в прошлое невозможно, это не физичное явление.
Рассмотрим движение тахиона в некой движущейся ИСО. Для определения его скорости применим лоренцево правило сложения скоростей. Особенностью любой заданной наперёд скорости тахиона в этом случае является то, что всегда существует ИСО, в которой эта скорость становится неограниченность сверху, то есть бесконечно большой или мгновенной. Найдём скорость такой ИСО, в которой скорость тахиона будет равна бесконечности:
u – скорость исходной ИСО;
V – скорость тахиона в системе покоя этой ИСО;
v – скорость искомой ИСО, в которой V становится бесконечно большой.
Мы используем систему измерений, в которой скорость света равна единице. Легко заметить из уравнения, что парадокс возникает в случае разнонаправленного движения двух систем, то есть искомая ИСО движется со скоростью v в отрицательном направлении, поэтому:
Скорость тахиона окажется равной бесконечности, если скорость v этой системы отсчета будет равна:
При этом скорость тахиона u в исходной системе отсчета может быть любой, лишь бы больше скорости света, пусть даже на незначительную величину. Например:
Эти аналитические выкладки можно наглядно изобразить на динамических диаграммах Минковского.
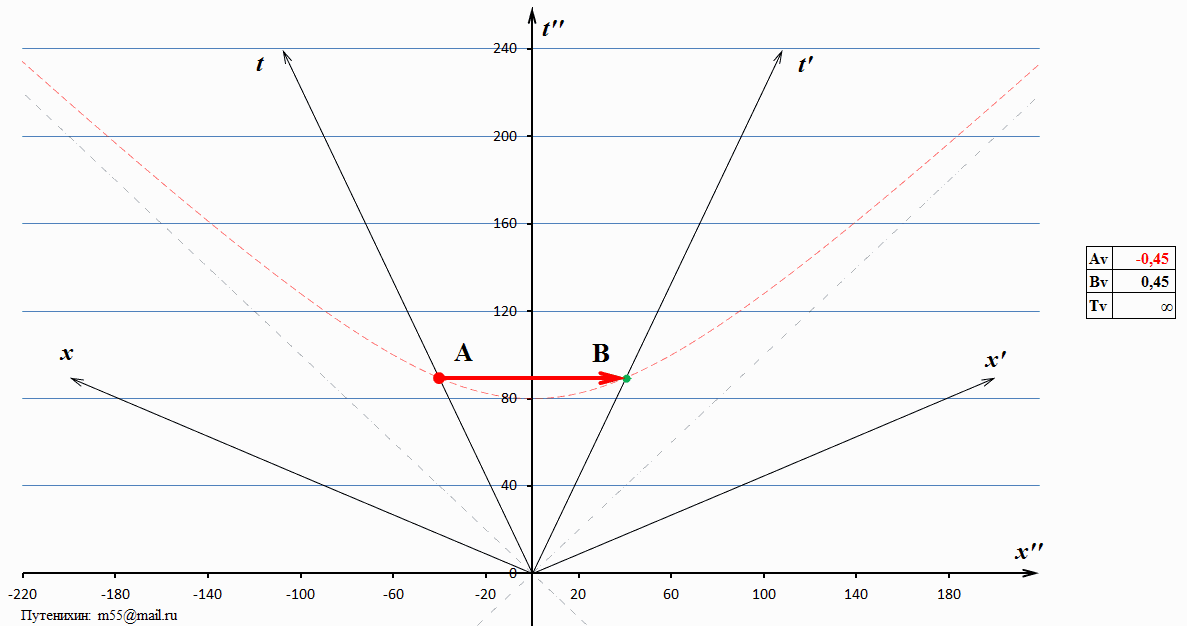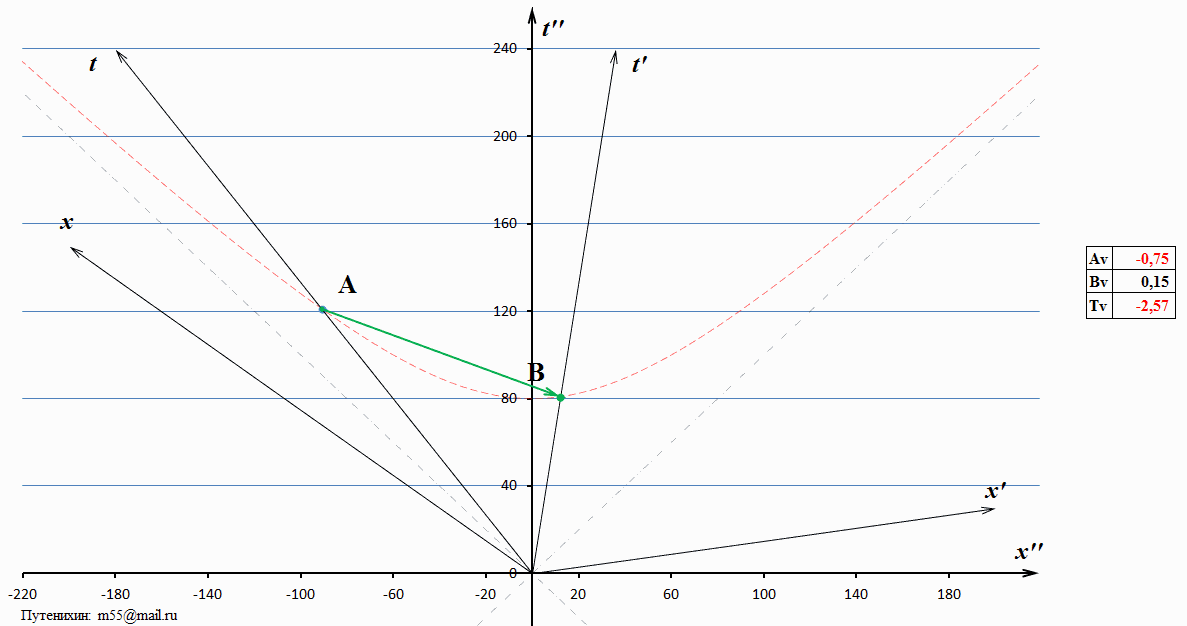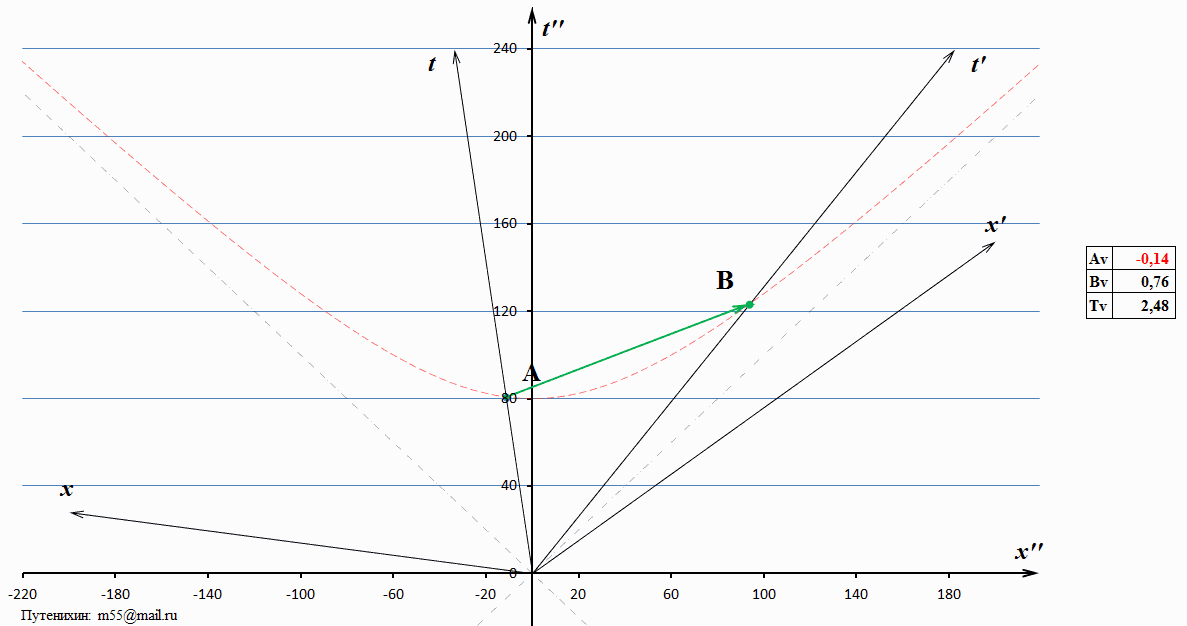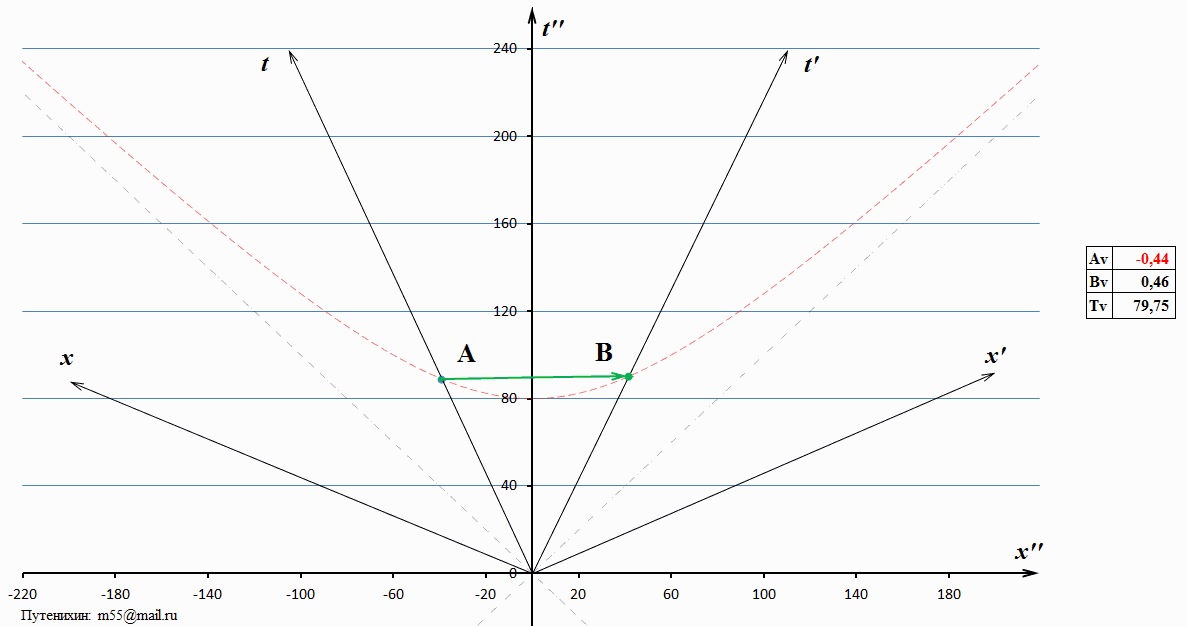
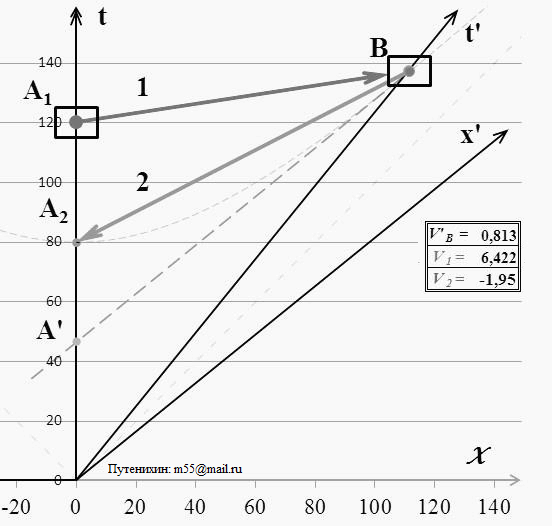
Рис.1 Динамические диаграммы Минковского, на которых видно, что при изменении скорости ИСО с движущимся в ней тахионом в лабораторной системе отсчета, скорость тахиона может быть равна бесконечности. При некоторых скоростях тахион движется в обратном направлении времени – в прошлое.
На диаграмме изображены две ИСО – излучающая и получающая тахион, частицу, движущуюся быстрее скорости света. Скорость излучающей ИСО зависит от относительной скорости некоторой лабораторной, условно неподвижной системы. Мы можем выбрать такую лабораторную систему, в которой скорость тахиона может быть равна бесконечности. При некоторых других скоростях лабораторной системы тахион демонстрирует движение в прошлое. Скорость тахиона в исследуемой, исходной системе отсчета на диаграмме взята незначительной – около 1,5 скоростей света. Все события рассматриваются в моменты времени различных лабораторных системах отсчета, когда тахион пересекает их. Это приблизительно от 80 до 90 единиц времени. Обратим внимание на то, что концы тахиона «скользят» по гиперболе – изохроне. Изохрона – это линия, отсекающая на всех ИСО равные моменты времени от начала движения. Следовательно, такое скольжение означает, что излучение и поглощения тахиона с любой точки зрения произошло в системах А и В в одно и то же время по их собственным часам. Понятно, что иначе и быть не может: из какой бы системы отсчета мы не смотрели, по собственным часам А и В события излучения и поглощения имеют единственное значение.
Каждой системе отсчета соответствуют свои относительные скорости систем А и В. Можно сказать и так: мы перескакиваем из одной лабораторной системы в другую, считая, что изменяется именно скорость этой лабораторной системы. Диаграмма разбита на три диапазона относительных скоростей, или, то же самое, скоростей лабораторной системы отсчета. Первый диапазон – это системы отсчета, с точки зрения которых тахион движется нормально из прошлого в будущее. В рядом помещённой таблице показаны параметры движения: скорости тахиона и двух ИСО, обменивающихся этим тахионом. Второй интервал, вернее, это даже и не интервал, а единственная система покоя, в которой скорость тахиона равна бесконечности. Мировая линия тахиона в этой системе покоя отображена жирной красной стрелкой. Как видно из таблицы, этому случаю соответствуют равные и противоположно направленные скорости обменивающихся тахионом ИСО А и В. В этом случае лабораторная система является для них средней или симметричной. К третьему интервалу скоростей относятся все лабораторные ИСО, в которых тахион имеет нефизические параметры движения.
Помимо сверхсветовой скорости тахион ещё и движется в прошлое. Явление движения в прошлое присуще исключительно специальной теор ии относительности. Только её математика в применении к сверхсветовым объектам неизбежно приводит к мгновенной связи и к нефизичному явлению – движению в прошлое. Однако, представить себе устройство, посылающее сигнал в прошлое, невозможно. Разумеется, речь не идёт о фантастических романах и мист ике.
Кроме того, бесконечно большая скорость вынуждает специальную относительность делать абсурдные выводы. Для любой ИСО, кроме изображенной на рисунке лабораторной системы и ей подобных, скорость тахиона будет отличной от бесконечности, от мгновенной передачи. Однако, предположим, что сигнал был отправлен через всю Вселенную. С точки зрения рассмотренной лабораторной системы отсчета – мгновенно, от планеты на одном краю Вселенной к планете на другом. В идеале, отправлены прямое и ответное письма. Это легко проверить в системе покоя на диаграмме, просто перехватив часть этих посланий. Как видно из диаграмм рис.1, существуют такие ИСО, в которых скорость этого тахиона (письма) лишь превышает скорость света, но не мгновенная. Следовательно, такая ИСО, например, вблизи одной из двух упомянутых планет не сможет объяснить подобный обмен письмами. В том числе и те, что изображены на диаграмме. С их точки зрения потребуется около 20 миллиардов лет (в их системах покоя тахион движется всё-таки быстрее света), чтобы письмо дошло до адресата, а ответ – до отправителя. Системы отсчета перестают быть равноправными, как того требует теор ия относительности.
В сверхсветовых «расширениях» специальной относительности главным инструментом на правах дополнительного постул ата в настоящее время используется так называемый принцип реинтерпретации. Согласно этому принципу, тахион, движущийся в прошлое и имеющий вследствие этого отрицательную энерги ю, может рассматриваться как антитахион, движущийся нормально в будущее и имеющий положительную энерги ю. Однако, за этой вроде бы научной фразой скрывается абсурдная суть. Никто из сторонников реинтерпретации не желает видеть, что разумное и логичное на первый взгляд «испускание антитахиона» означает не существующее испускание, испускание которого не было:
Рис.2 Копия иллюстрации к статье E.Recami «The Tolman-Regge Antitelephone Paradox: Its Solution by Tachyon Mechanics». Ответный тахион 2 посылается в обратном направлении времени.
На рисунке 2 приведена копия иллюстрации к статье E.Recami «The Tolman-Regge Antitelephone Paradox: Its Solution by Tachyon Mechanics». В статье рассматривается так называемый «парадокс антителефона» и предлагается его решение в рамках тахионной механики на основе принципа реинтерпретации. Из системы А посылается тахион 1 в систему В, откуда в систему А посылается ответный тахион 2. Как видим, по условиям задачи в системе покоя А тахион 2 движется в обратном направлении времени, в прошлое. В качестве решения предлагается реинтерпретация второго тахиона. Он должен рассматриваться как антитахион, испущенный системой А. В этом случае, казалось бы, всё встаёт на свои места: антитахион движется нормально – из прошлого в будущее. Антитахион в этом случае испущен системой А. Но возникает вопрос: на каком основании утверждается, что система А испустила, эмитировала антитахион? Этого не было! Нет и не было в системе А устройства, предназначенного для испускания, эмиссии антитахионов и в указанный момент времени в системе А антитахионов никто не излучал.
Такое «испускание, которого не было» является абсурдным заявлением, противоречащим логике и научным принципам. Как можно говорить об испускании какой-либо частицы в некоторый момент времени, если в этот момент никто и ничего не испускал? Правильным решением этой проблемы является только одно: специальная теор ия относительности неспособна решать задачи со сверхсветовыми сигналами.
Кроме того, как известно, сверхсветовые корреляции, взаимодействия явно, в реальности, в конкретном физическом эксперименте демонстрирует квантовая запутанность, нелокальность. Однако, никакое взаимодействие, каким бы иллюзорным и мист ическим (нелокальным) оно ни казалось, не может происходить без обмена теми ли иными материальными носителями. Таким образом, квантовая нелокальность не только плохо согласуется с теор ией относительности, но и определённо противоречит ей.
Собственно, иллюзорность тахиона не является исключительной особенностью специальной относительности. Скорость его движения, превышающая скорость света, автоматически приводит к появлению миражей. Действительно, мы никогда не наблюдаем какой-либо объект непосредственно. В наши глаза поступает свет, отраженный от объектов. Таким отражающим или излучающим объектом можно рассматривать и тахион. Когда тахион стремительно пролетает мимо наблюдателя, то свет от него начинает поступать к наблюдателю после того, как сам тахион уже удалился. Это явление ничуть не противоречит и классической физике, оно не требует никаких релятиви стских преобразований.
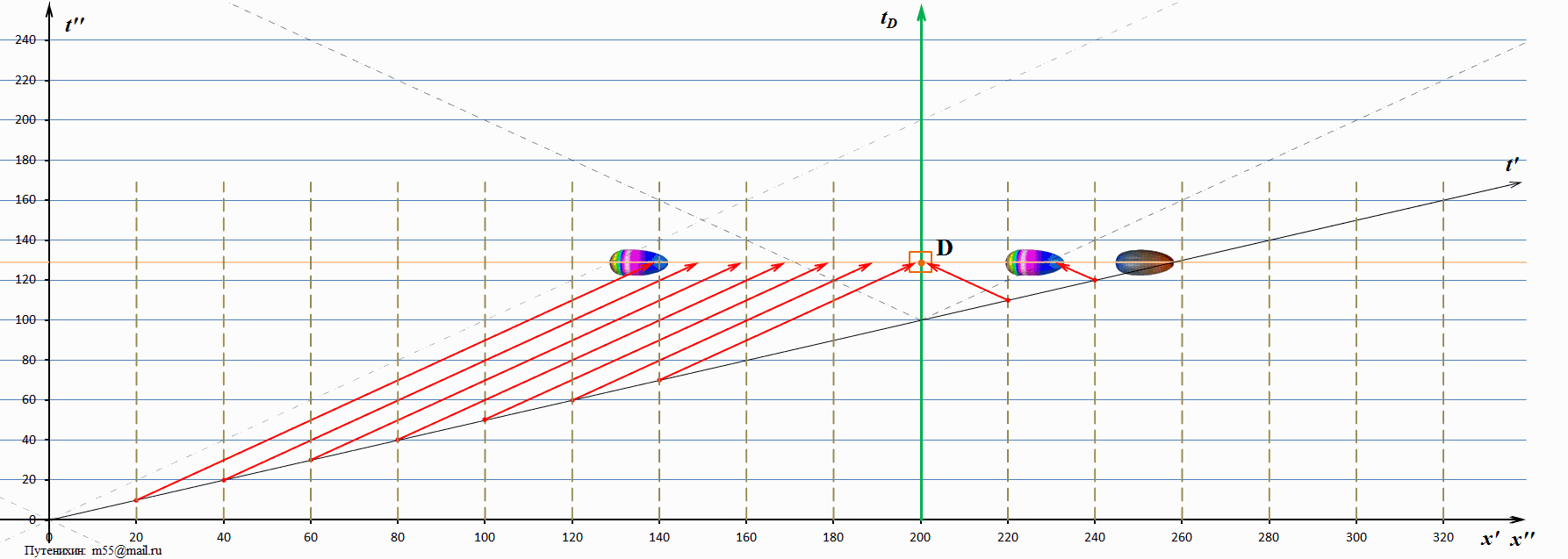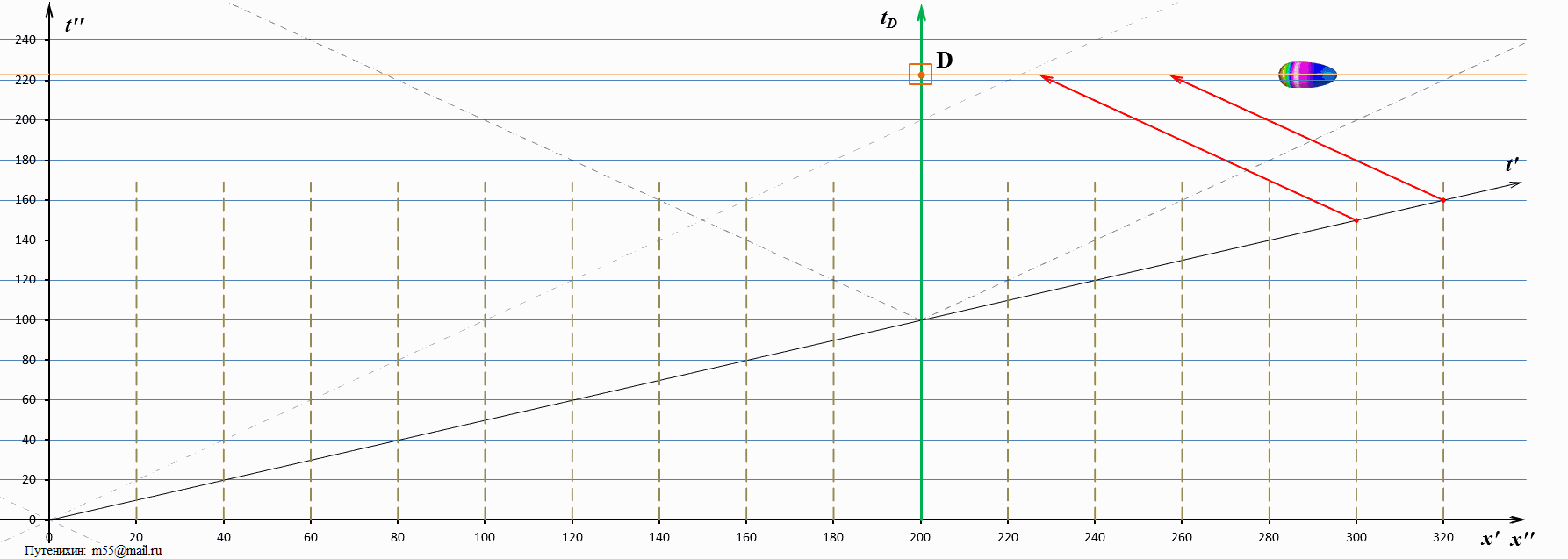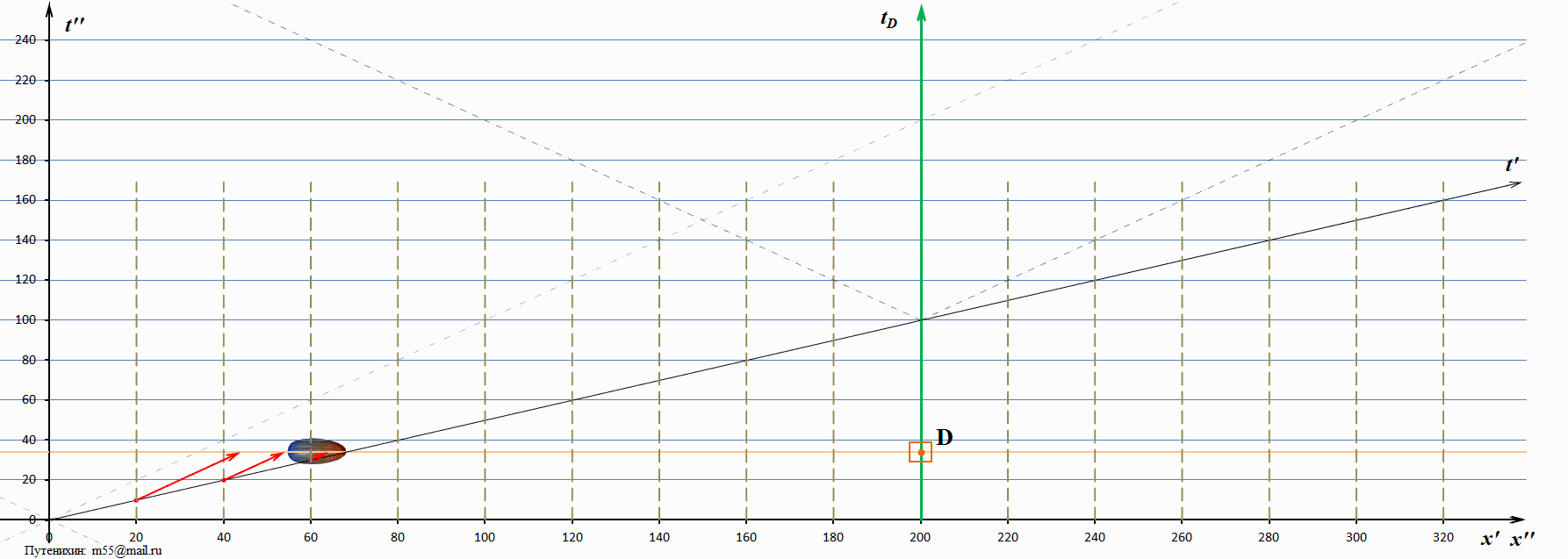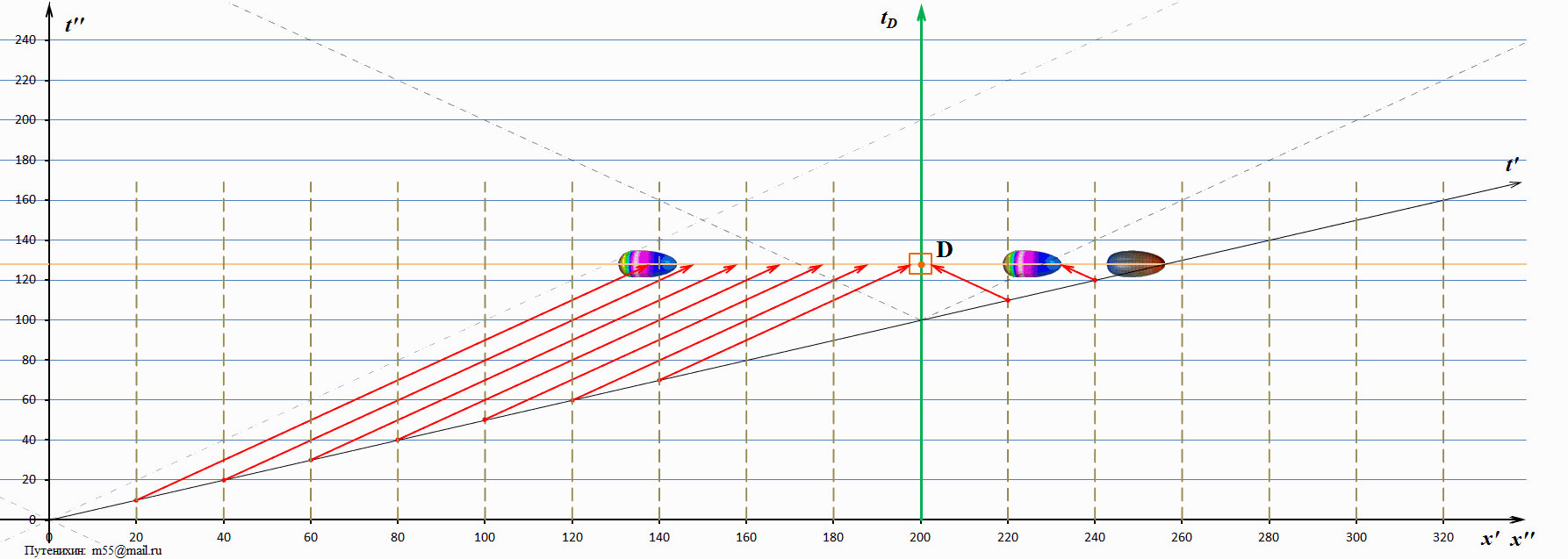
Рассмотрим, как выглядит процесс движения тахиона на динамических диаграммах Минковского. Для начала рассмотрим случай, когда скорость тахиона в 3 раза выше скорости света:
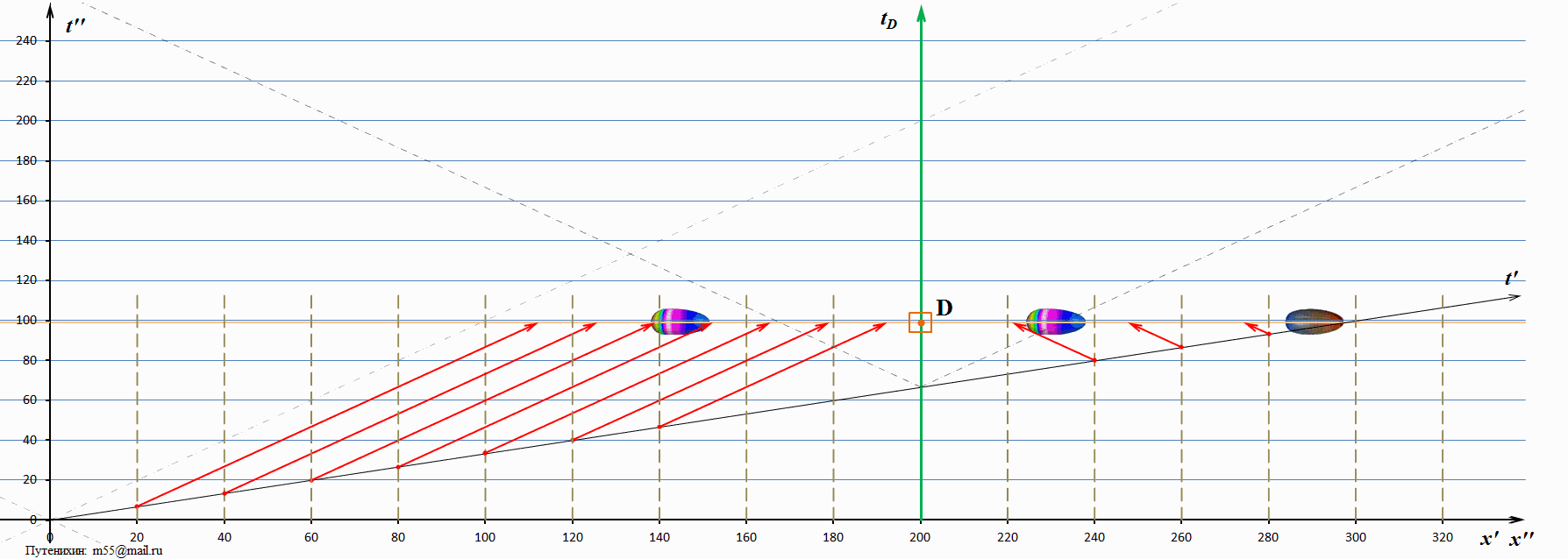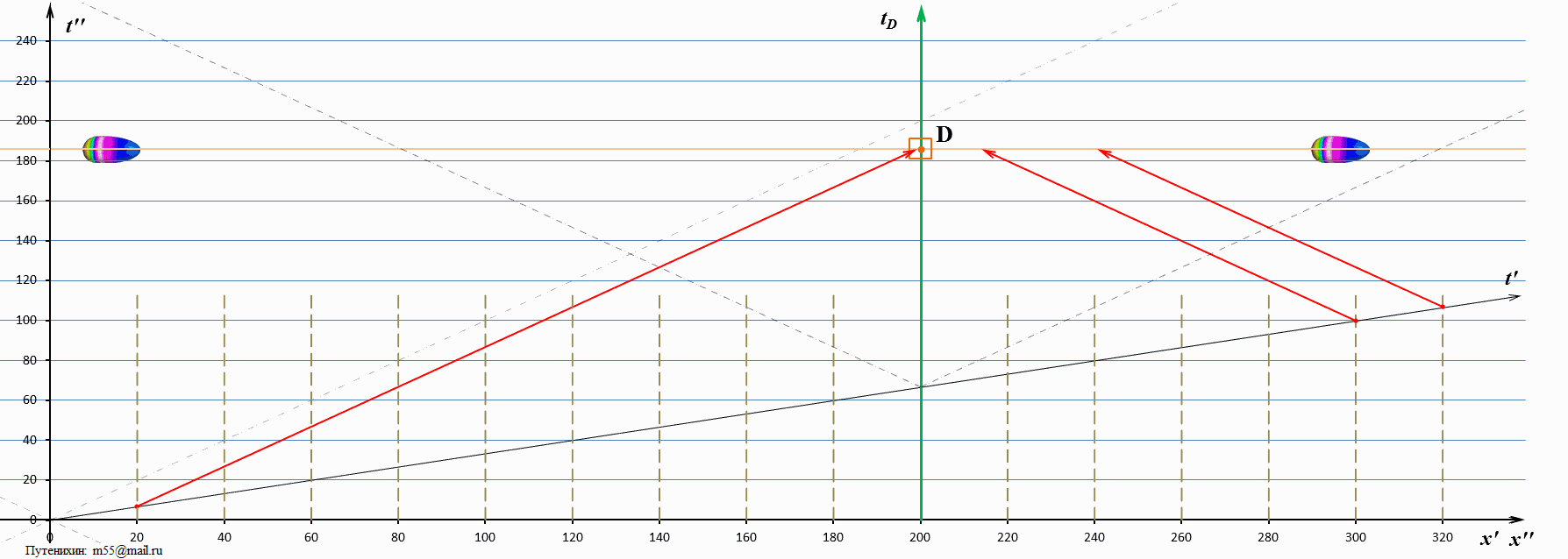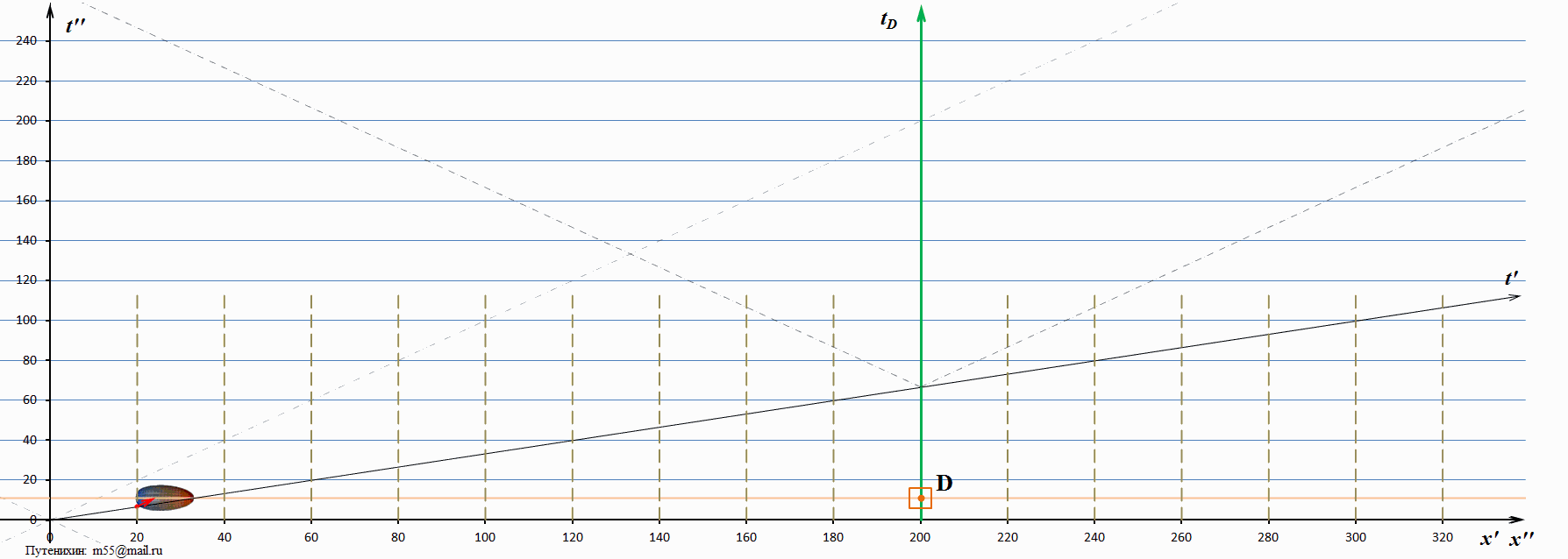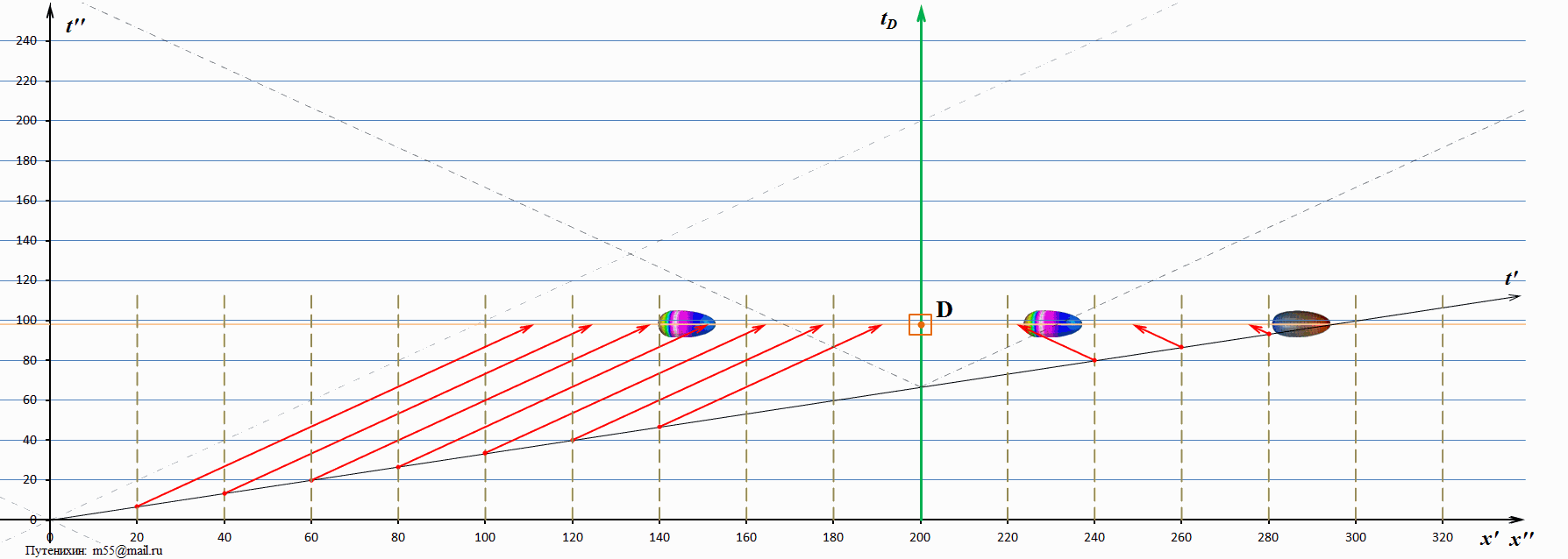
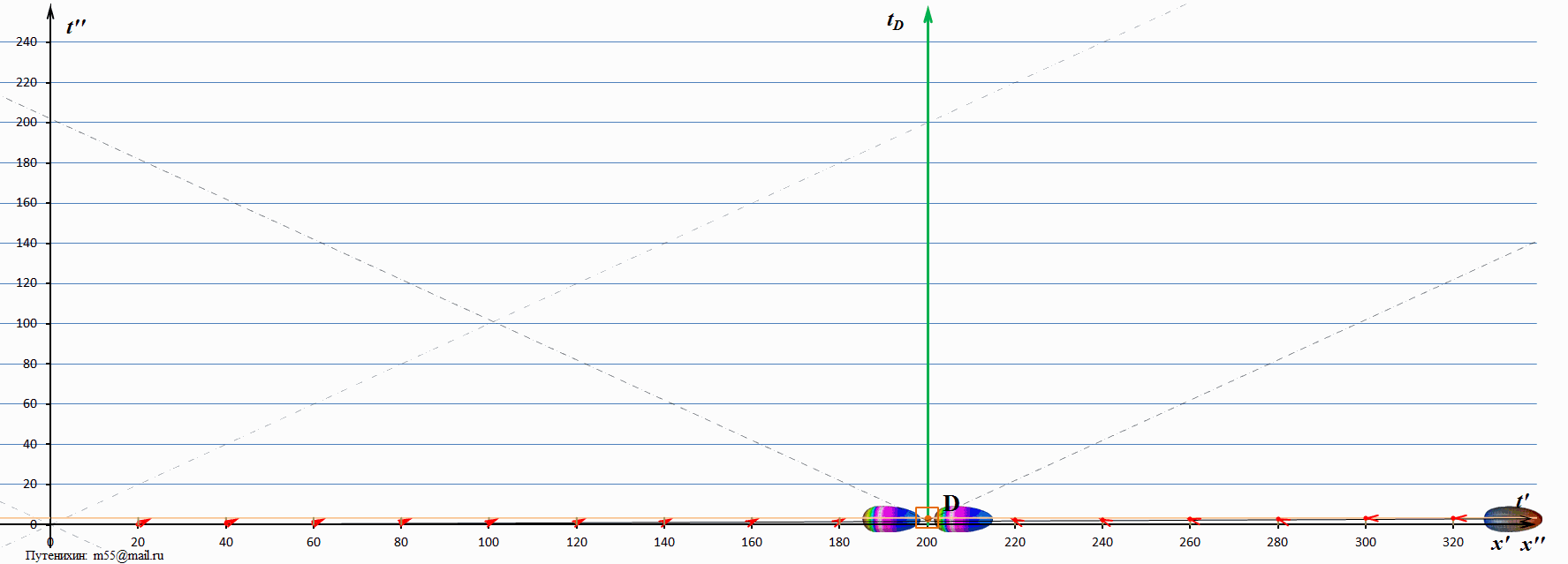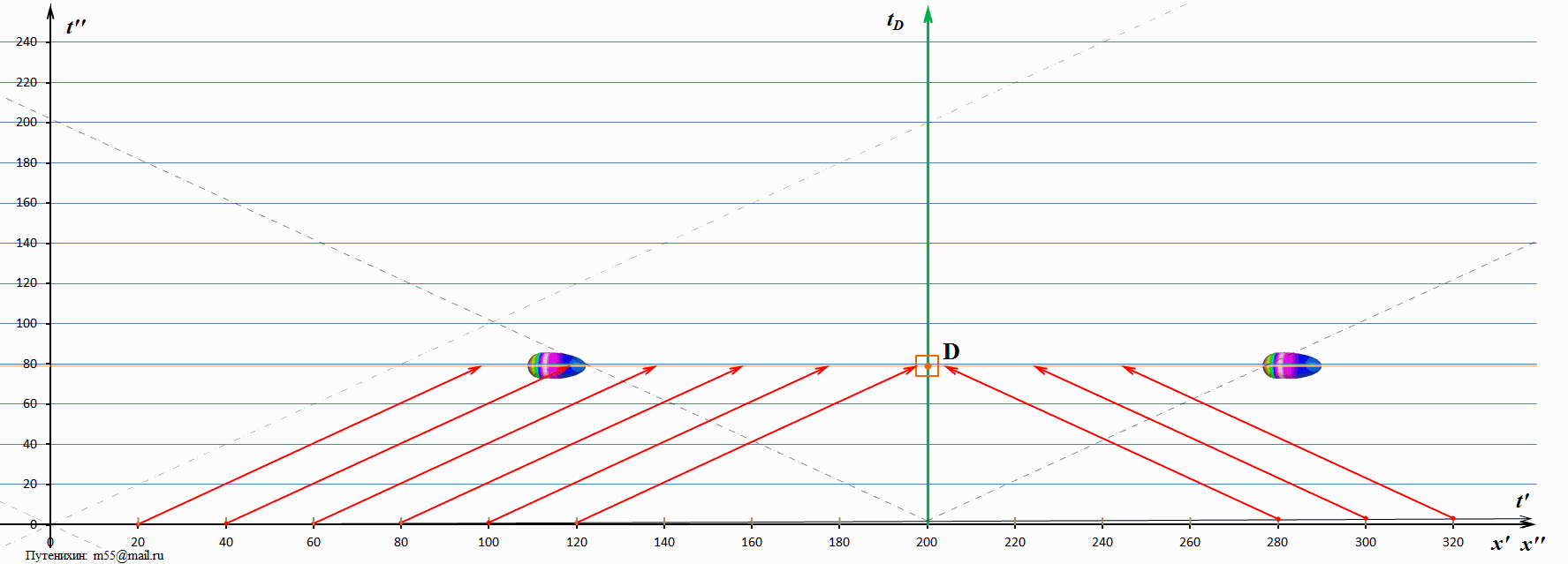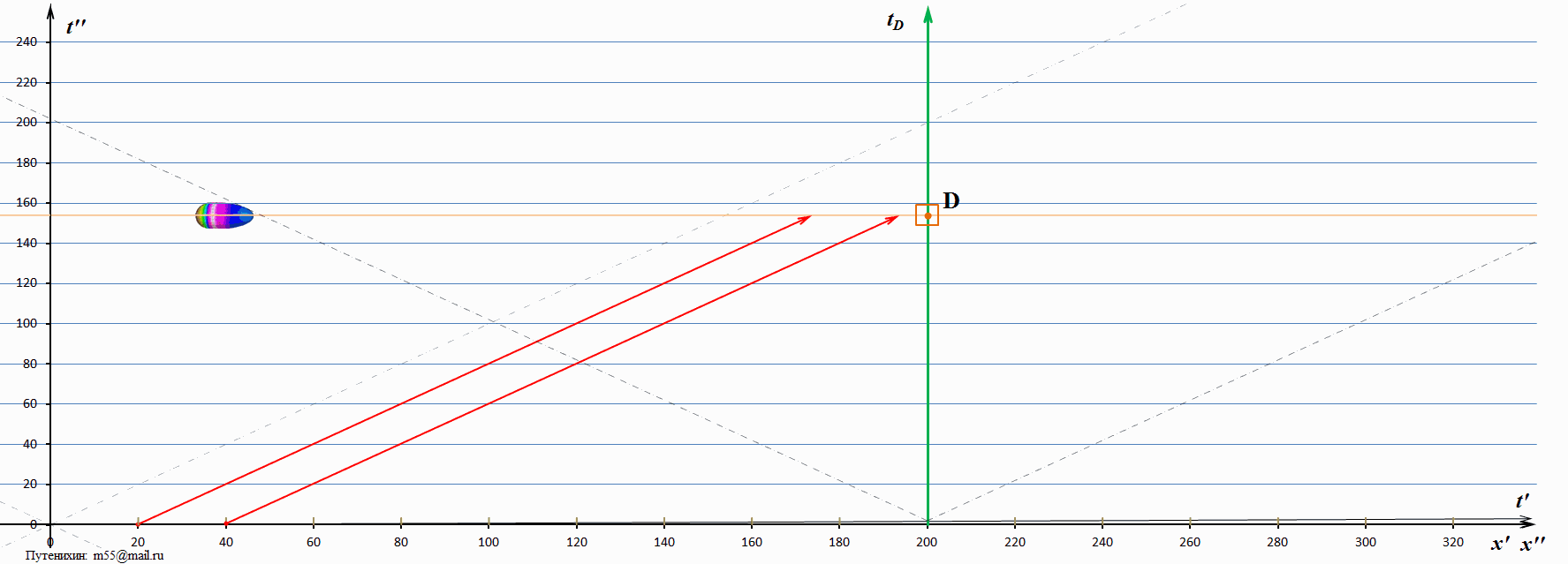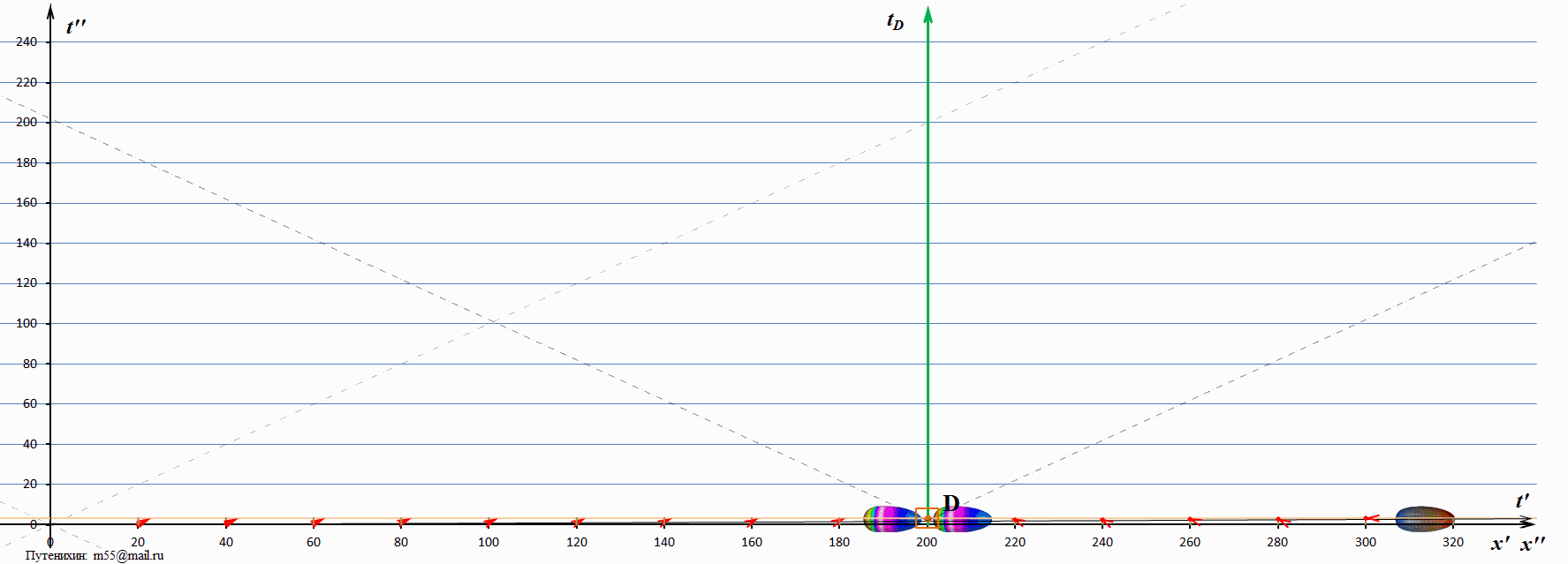
В системе покоя диаграммы изображен наблюдатель D, находящийся на удалении 200 единиц от начала координат. Мировая линия tD наблюдателя D изображена зеленым цветом. Все происходящие на диаграммах события находятся на одной горизонтали, показанной оранжевой линией – линией настоящего (времени) системы покоя. Всё, что ниже этой линии – уже произошло, всё, что выше неё – может произойти в будущем. В начальный момент времени из начала координат излучается тахион, имеющий в рассматриваемом случае скорость 3с – три скорости света. На его пути через каждые 20 единиц размещены регистрирующие устройства, которые изображены серыми штриховыми вертикальными отрезками. Когда тахион достигает каждого из этих регистраторов, он либо зажигает на нём лампу, либо включает всю свою бортовую иллюминацию, либо подаёт какой-то другой сигнал со скоростью света. Самого тахиона наблюдатель D не видит, он видит только излучаемые тахионом сигналы из этих контрольных точек.
В момент времени 66,7 единиц в рассматриваемом случае тахион достигает наблюдателя. В этот момент и начинается процесс регистрации наблюдателем D сигналов, инициированных тахионом. Поскольку скорость тахиона велика, он быстро проскакивает точку встречи и, удаляясь, более не оказывает никакого влияния на процесс. К наблюдателю начинают поступать сигналы из точек регистрации: со стороны излучения и со сторону, куда тахион удалился. Эти сигналы на диаграммах изображены красными стрелками. Нижний конец стрелки (отмечен точкой) связан с моментом излучения сигнала, а верхний, стрелка – показывает место в пространства-времени, где находится носитель сигнал (фотон). В тот момент, когда очередной носитель сигнала – стрелка достигает наблюдателя D, наблюдатель фиксирует «вспышку» или «картинку» тахиона, соответствующую его положению в момент времени, когда была инициирована эта вспышка. То есть, наблюдатель как бы будет видеть тахион в этой точке пространства, как это показано на диаграмме в виде изображений тахиона. Но, напомним, тахиона там нет, это лишь свет (сигнал) пришедший от тахиона, когда он там находился. Тахионы, изображенные на диаграммах как две более красочные его копии, являются на самом деле миражами.
Очевидно, что мираж, удаляющийся в сторону излучения, виден наблюдателю как лицевая сторона тахиона («лицо» тахиона). Напротив, мираж, удаляющийся в сторону движения тахиона, виден наблюдателю со стороны его «затылка».
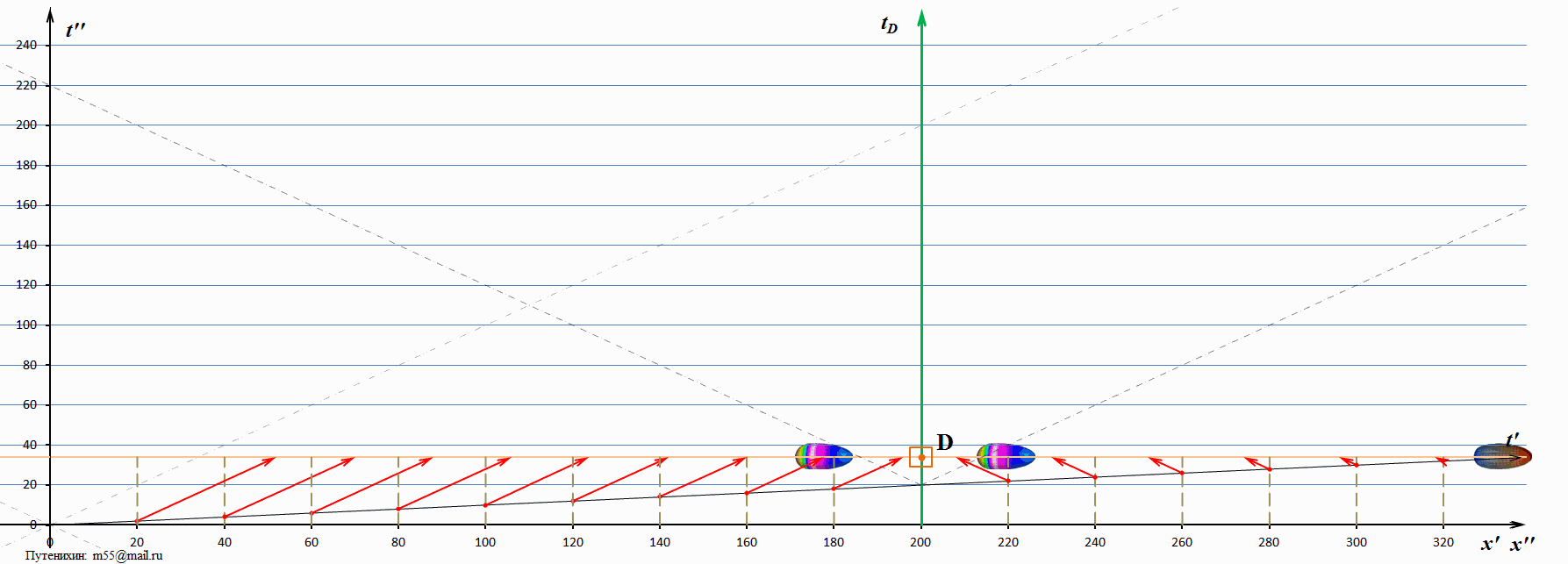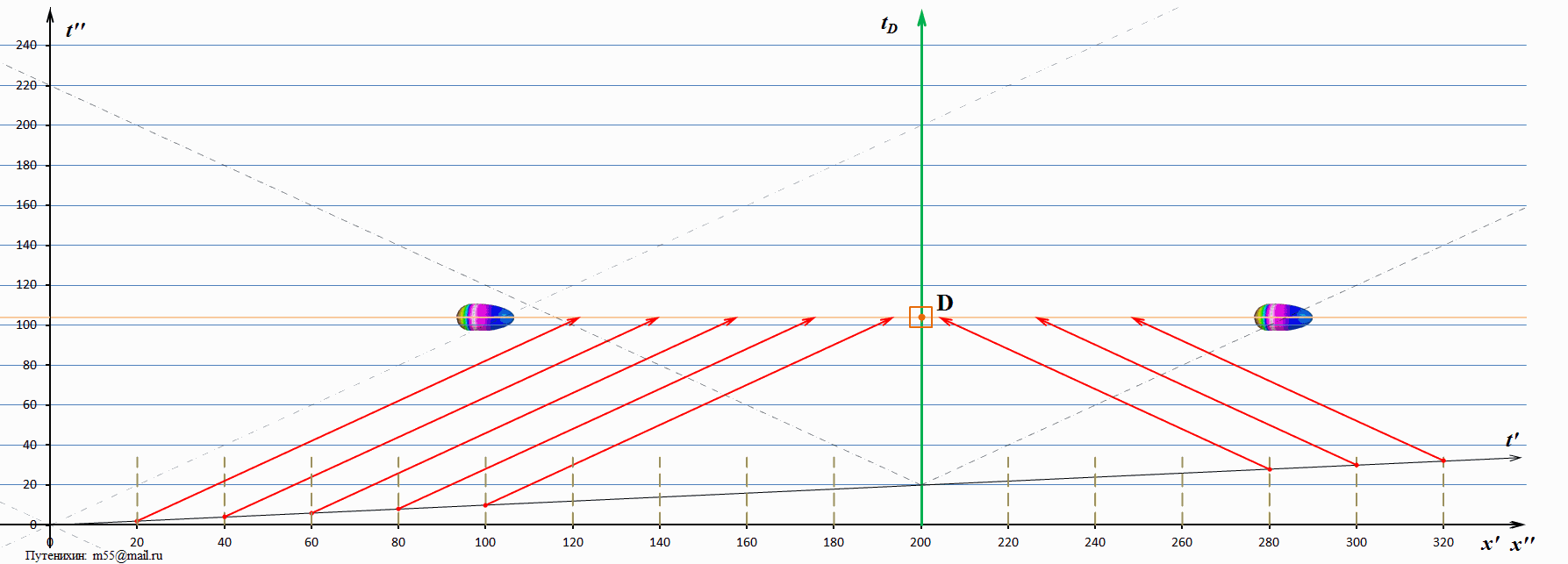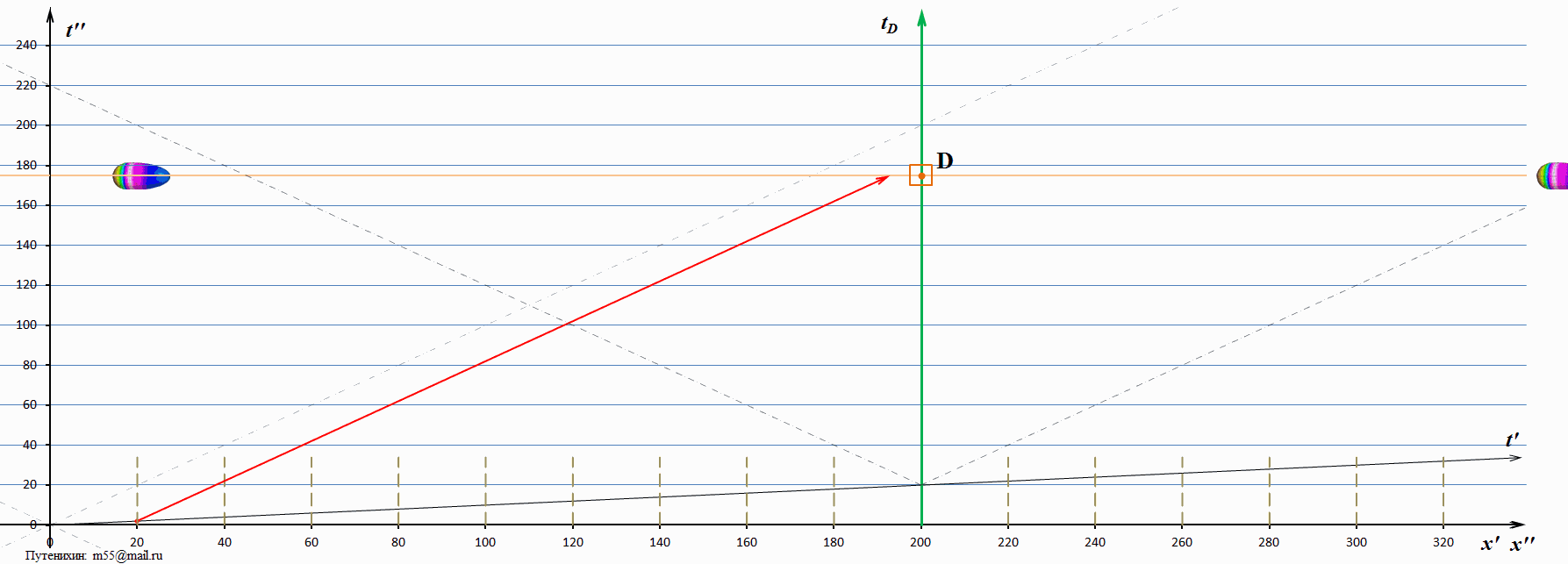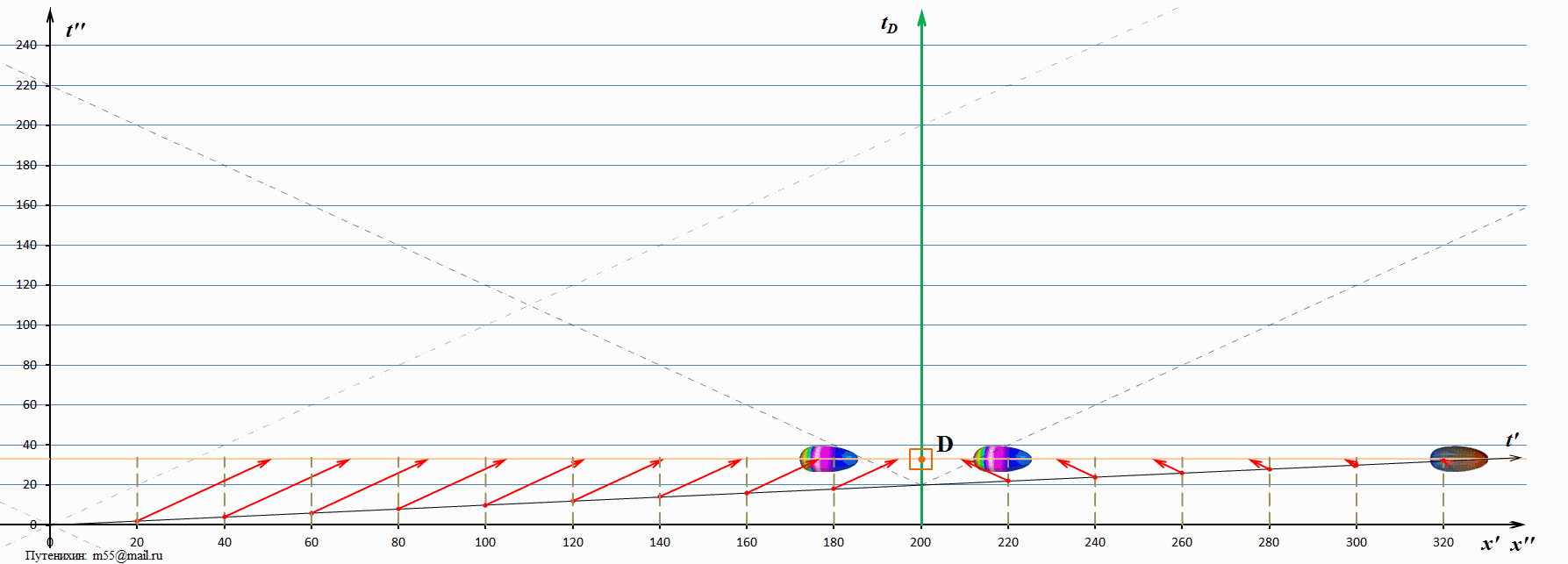
На диаграмме наклонными штриховыми линиями изображены мировые линии света. Видна интересная закономерность: «возвращающийся» мираж тахиона имеет скорость, превышающую скорость света, но меньшую чем сам тахион. А вот мираж, движущийся вслед за тахионом, имеет скорость меньшую, чем скорость света. Возможно, это связано с достаточно низкой скоростью тахиона? Посмотрим диаграммы, на которых тахион имеет скорость в 10 скоростей света:
На этой диаграмме, как и на предыдущей мираж тахиона, движущийся вслед за ним, также движется над мировой линией света, то есть его скорость и в этом случае меньше скорости света. Точкой видимости на мираже тахиона является его «затылочная» часть, именно она оказывается выше мировой линии света. Для того чтобы окончательно убедиться в обнаруженной закономерности, рассмотрим ещё одну диаграмму, на которой скорость тахиона превышает скорость света в 100 раз:
Рис.5 Динамические диаграммы Минковского: мираж тахиона, движущийся вслед за ним, имеет скорость, меньшую скорости света. Скорость тахиона в 100 раз превышает скорость света.
На диаграмме мировая линия тахиона почти слилась с горизонтальной осью, а сам тахион на динамической диаграмме пролетает настолько быстро, что его почти не видно. Здесь уже можно окончательно убедиться, что скорость миража тахиона, движущегося вслед за ним, меньше скорости света. При этом ясно, что увеличение скорости тахиона приводит к приближению скорости миража к скорости света. Второй, «возвращающийся» мираж, как видно на диаграммах, наоборот, уменьшил свою скорость, максимально приблизив её к скорости света. На этой диаграмме «видимой» частью миража является его лицевая сторона, и она практически скользит по мировой линии света. Это и означает, что его скорость близка к скорости света. Заметим, что скорость самого тахиона, вызвавшего эти миражи, превышает скорость света в 100 раз.
В заключение логично рассмотреть и обратную ситуацию, случай, когда скорость тахиона близка к скорости света. Слишком маленькую скорость брать неудобно, поскольку вся картина быстро уходит за пределы диаграммы. Поэтому возьмём скорость, равную двум скоростям света:
Рис.6 Динамические диаграммы Минковского: скорость тахиона в 2 раза выше скорости света.
Как и следовало ожидать, скорость «догоняющего» миража стала ещё меньше, а скорость «возвращающегося» миража – увеличилась.
На рассмотренных диаграммах тахионных миражей мы не использовали математику специальной теор ии относительности. Единственное, что присутствует здесь от неё – это динамические диаграммы Минковского, которые в данном случае демонстрируют свою высокую наглядность и, можно сказать, универсальность.
Необходимо указать, что траектории движения миражей были рассчитаны из очевидных логических соображений и интуитивно найденных соотношений. Для вычисления скоростей антитахиона – «возвращающегося» миража и «догоняющего» миража были использованы уравнения:
vвозвр – скорость «возвращающегося» миража;
Итак, на вопрос, вынесенный в заголовок статьи можно ответить: скорость тахиона определяется только скоростью системы отсчета и может иметь величину от минимально превышающей скорость света до бесконечности.
Оценить статью можно после того, как в обсуждении будет хотя бы одно сообщение.
Тахион
Гипотетические поля, соответствующие описанной частице, называются тахионными полями. Обычно в качестве таковых рассматриваются поля, подчиняющиеся уравнению Клейна-Гордона (или Дирака, Янга — Миллса [3] и т. п.) с противоположным знаком у массового члена (то есть с отрицательным квадратом массы; иногда, как в случае уравнения Дирака, где параметр массы входит в первой степени, его приходится делать мнимым — или матричным и т. п. — явно). Интересно заметить, что подобные поля достаточно легко реализуются в том числе в простых механических моделях, а также могут встречаться при описании неустойчивых сред в физике твердого тела.
Содержание
История
Впервые тахионы описал Зоммерфельд, затем тахионы теоретически исследовали сравнительно многие физики, среди них можно выделить таких, как Сударшан, Олекса-Мирон Биланюк, (en:Vijay Deshpande), и Джеральд Фейнберг (Gerald Feinberg). Последнему принадлежит и сам термин.
Базовые понятия
Частица с мнимой массой
Простейший способ формального введения тахиона в рамках специальной теории относительности состоит в том, чтобы сделать в формулах для энергии и импульса
массу 
— не действительным, как обычно, а (чисто) мнимым числом.
Тогда, полагая, что энергия и импульс должны быть действительными, приходим к необходимости 
c» border=»0″ />, то есть получаем тахион — частицу, скорость которой не может быть меньше скорости света. При замедлении такой частицы энергия увеличивается, причем при замедлении до скорости света — увеличивается бесконечно, то есть очевидно, затратив конечную энергию, тахион нельзя затормозить до скорости света (как обычную массивную частицу нельзя до неё разогнать).
При этом можно заметить, что обычное соотношение энергии и импульса
из-за того, что в случае тахиона 
, приводит к тому, что не при всех импульсах энергия действительное число. Решение с мнимой энергией соответствует экспоненциальному росту (неустойчивости) тахионного поля при небольших пространственных частотах, то есть в этом случае нет бегущей волны.
Тахионные поля
Простейший способ описания (конструирования) тахионного поля в терминах полевых уравнений — использование уравнений, аналогичных уравнению Клейна — Гордона для скалярного или векторного тахиона:
и тому подобные обобщения, только с противоположным знаком массового члена 
в первом случае, и явном использовании мнимого во втором (то есть в обоих случаях опять можно использовать мнимую массу; вообще же говоря, масса может быть не обязательно просто мнимым числом, но и каким-то другим объектом, например, матрицей, лишь бы её квадрат был отрицательным).
Иными словами, обозначив мнимую массу 
, где 
— действительное число, можно записать для случая тахионных полей уравнения Клейна — Гордона — Фока и Дирака так:
Подставив бегущую волну 
в любое из этих уравнений, получим такое соотношение [5] для 
и 
(для простоты можно проделать это в одномерном варианте), что групповая скорость 
окажется большей, чем 
.
Тахион и тахионное поле
При кажущейся синонимичности понятий тахиона и тахионного поля (как это бывает с обычными полями и обычными частицами в квантовой теории поля), следует иметь в виду, что здесь могут иметь место некоторые терминологические и содержательные особенности.
Хотя по определению тахионным полем можно считать поле, групповая скорость волн которого больше скорости света, тем не менее, не все типы возбуждений тахионного поля распространяются со столь большой скоростью. Так, например, передние фронты ограниченных в пространстве волновых пакетов тахионного поля, насколько известно (из расчетов и экспериментов с формальными аналогами), практически во всех исследованных случаях распространяются не быстрее, чем со скоростью с (а именно только такие волновые пакеты пригодны для того, чтобы быть сигналами при передаче информации).
С другой стороны, тахион как частица — результат квантования тахионного поля. Такое квантование прежде всего представляет проблему само по себе, так как содержит неустойчивый сектор (длинноволновый). Казалось бы, можно ограничиться только достаточно коротковолновым сектором, в котором этой проблемы нет. Однако, так ограничивая спектр, мы оказываемся ограничены случаем плохо локализованных волновых пакетов (то есть бесконечно протяженных возбуждений), которые в принципе нельзя, например, излучить за конечное время в конечной области пространства. Если же мы хотим исследовать волновые пакеты конечного пространственного размера, мы должны использовать весь спектр (включая и сектор неустойчивости или мнимой энергии).
В этом видится серьёзное содержательное расхождение между понятием тахионного поля и тахиона как частицы. В частности, если совсем игнорировать тахионное поле и рассматривать тахион как чисто классическую (не квантовую) частицу (материальную точку), соотношение между энергией и импульсом каковой описано выше, то действительно можно столкнуться с парадоксом причинности, описанным ниже, а путь, на котором проблема могла бы быть решена, остается тогда неясным (впрочем, принципиально чисто классическая частица в современной физике в любом случае была бы предметом очень больших сомнений).
Механическая модель
Простой и достаточно наглядной механической моделью скалярного тахионного поля (на одномерном пространстве) может служить натянутая струна (нить), лежащая без трения сверху вдоль горизонтального цилиндра.
Одним из ценных свойств такой модели является интуитивная очевидность некоторых фактов, прежде всего того факта, что концепция внутренне непротиворечива и в принципе реализуема, а в данном случае и того важного факта, что тахионное поле, по крайней мере в варианте этой модели, в принципе не может нарушить принцип причинности (а лоренц-инвариантность прямо следует из уравнения движения), а это значит, что в принципе возможны тахионные поля, не нарушающие принципа причинности. Также из неё довольно очевидно, что для принципиальной невозможности взаимодействия тахионного поля с нетахионными полями нет достаточных оснований. Единственной очевидной проблемой остается проблема неустойчивости. Также эта модель, по-видимому, не дает радикального интуитивного ответа на вопрос о возможности и условиях распространения тахионной волны быстрее света (хотя эта модель может быть полезна и для исследования двух последних вопросов, однако тут она не приносит в сущности чего-то нового по сравнению с обычным исследованием решений исходного уравнения).
Аналогии
Формальными аналогами фундаментальных тахионных полей являются, среди прочего, различные типы возбуждений в твердом теле (или других средах).
В некоторых случаях при этом речь идет о том, что, как и в случае гипотетических фундаментальных тахионов, вопрос стоит о том, что возмущение распространяется быстрее, чем свет в вакууме (см. ссылку об оптических тахионах). Последние исследовались с особенной тщательностью, и, насколько известно, хотя распространение максимума огибающей волнового пакета быстрее света в вакууме в таких случаях действительно может наблюдаться, однако с помощью него не может передаваться быстрее света в вакууме какая-либо информация; в частности, передний фронт такого волнового пакета, какой бы ни была его форма, по сообщениям исследователей, никогда не распространяется быстрее, чем c.
Ясно, что наряду с теоретическими расчетами, использование аналогии с такими вполне наблюдаемыми реально уже сейчас системами достаточно полезно для теоретического исследования гипотетических фундаментальных тахионов.
Трудности
Тахионы до сих пор экспериментально не обнаружены. При этом существует несколько вопросов, которые могут до некоторой степени поставить под сомнение если не саму теоретическую возможность существования тахионов, то некоторые из представлений, возникающих при первом взгляде.
Проблема нарушения причинности, неустойчивость, действительно ли тахион так быстр
Одна из основных проблем, связанных с тахионами — нарушение причинности, появляющееся при наивном рассмотрении, когда тахион уподобляется обычному «шарику», движущемуся быстрее света, который наблюдатель может по своему желанию испускать, передавая с ним быстрее света энергию и информацию (направленные сигналы).
Вторая проблема — свойство нестабильности тахионных полей. Необычный знак массового члена приводит к неограниченному [6] экспоненциальному росту мод тахионного поля с небольшими пространственными частотами, что приводит к хаосу или к ситуации, маскирующей ожидаемые эффекты (например, распространение волновых пакетов), что, с другой стороны, может способствовать устранению проблемы нарушения причинности.
Часто утверждалось, что тахионы вообще не могут передавать информацию, иначе их наличие противоречило бы принципу причинности (выполнение принципа относительности — лоренц-инвариантность подразумевается [7] ), от которого современная физика пока не готова отказываться, хотя он и не является абсолютно обязательным (ни одна теория не содержит его в качестве постулата). Предпринимались попытки по разному обосновать невозможность передачи информации тахионами, например, принципиальной нелокализуемостью тахиона либо невозможностью отличить его воздействие, вызванное намеренно возбужденной волной, от его спонтанной случайной флуктуации, связанной с его неустойчивостью. Однако требование, чтобы тахионное поле вообще не могло передавать информацию, слишком сильно; на самом деле, для этого следует потребовать лишь невозможность передавать информацию быстрее света. Возможно, у тахионного поля могут существовать как типы возбуждений, двигающиеся быстрее света (которые не могут переносить с собой информацию), так и двигающиеся не быстрее света (которые могут переносить с собой информацию).
Случай компактного пространства
В ряде ситуаций, при исследовании вопроса о том, приводит ли распространение информации и энергии со скоростью, большей c к нарушению принципа причинности, обычные рассуждения требуют по меньшей мере заметной модификации. Прежде всего, это случай компактного пространства (простейший, одномерный, пример такого пространства — окружность; на ней можно рассмотреть тахионные поля или частицы-тахионы). Особенность такого пространства в том, что на нём вовсе не эквивалентны (глобально) все лоренцевы (инерциальные) системы отсчета, напротив, существует только одна выделенная система отсчета, для которой пространственно-временные координаты однозначны и непрерывны, в остальных не удается избежать разрыва (скачка) времени при обходе окружности. Если же не все лоренцевы системы отсчета равноправны, то мысленный эксперимент с посылкой информационного сигнала в собственное прошлое не получается таким же, как в бесконечном пространстве. Это замечание не означает доказательства того, что фронт тахионной волны действительно может распространяться в этой ситуации быстрее света, а всего лишь ставит под сомнение теоретическое ограничение, связанное с упомянутым мысленным экспериментом.
Тахионы в различных теориях
Во многих современных теориях, включающих спонтанное нарушение симметрии (например, включающие механизм Хиггса как он включен в Стандартную модель), присутствуют поля (экспериментально всё ещё не обнаруженные), которые можно назвать в определенном смысле тахионными. Однако обычно такие поля имеют свойства тахионных лишь в области неустойчивости, имея и точки устойчивого равновесия («конденсат»), таким образом, можно считать их не соответствующими первоначальному понятию тахиона и тахионного поля, подразумевающему отсутствие минимумов потенциала, и модифицирующими само понятие тахиона. Однако современное словоупотребление обычно не считается с такими тонкими различиями; при этом само употребление слов тахионная конденсация (или просто конкретное описание вида потенциала) однозначно дает понять, о чём идет речь.