Информатика что такое дерево моделями каких систем могут служить деревья
Все что нужно знать о древовидных структурах данных
Jul 1, 2018 · 14 min read
Деревья прекрасны. Вот рисунок, который я сделал ребенком
Когда вы впервые учитесь кодировать, общепринято изучать массивы в качестве «основной структуры данных».
В конце концов, вы также изучаете хэш-таблицы. Для получения степени по «Компьютерным наукам» (Computer Science) вам придется походить на занятия по структурам данных, на которых вы узнаете о связанных списках, очередях и стеках. Эти структуры данных называются «линейными», поскольку они имеют логические начало и завершение.
Однако в самом начале и зучения деревьев и графов мы можем оказаться слегка сбитыми с толку. Нам привычно хранить данные линейным способом, а эти две структуры хранят данные совершенно иначе.
Данная статья поможет вам лучше понять древовидные структуры данных и устранить все недоразумения на их счет.
Из этой статьи вы узнаете:
Давайте начнем наше учебное путешествие 🙂
Определения
Когда вы только начинаете изучать программирование, обычно бывает проще понять, как строятся линейные структуры данных, чем более сложные структуры, такие как деревья и графы.
Деревья являются широко известными нелинейными структурами. Они хранят данные не линейным способом, а упорядочивают их иерархически.
Давайте вплотную займемся реальными примерами
Что я имею в виду, когда я говорю иерархически?
Представьте себе генеалогическое древо отношений между поколениями: бабушки и дедушки, родители, дети, братья и сестры и т.д. Мы обычно организуем семейные деревья иерархически.
Мое фамильное дерево
Приведенный рисунок — это мое фамильное древо. Тосико, Акикадзу, Хитоми и Такеми — мои дедушки и бабушки.
Тошиаки и Джулиана — мои родители.
ТК, Юдзи, Бруно и Кайо — дети моих родителей (я и мои братья).
Структура организации — еще один пример иерархии.
Структура компании является примером иерархии
В HTML, объектная модель документа (DOM) представляется в виде дерева.
Объектная модель документа (DOM)
Техническое определение
Дерево представляет собой набор объектов, называемых узлами. Узлы соединены ребрами. Каждый узел содержит значение или данные, и он может иметь или не иметь дочерний узел.
Первый узел дерева называется корнем. Если этот корневой узел соединен с другим узлом, тогда корень является родительским узлом, а связанный с ним узел — дочерним.
Все узлы дерева соединены линиями, называемыми ребрами. Это важная часть деревьев, потому что она управляет связью между узлами.
Листья — это последние узлы на дереве. Это узлы без потомков. Как и в реальных деревьях, здесь имеется корень, ветви и, наконец, листья.
Другими важными понятиями являются высота и глубина.
Высота дерева — это длина самого длинного пути к листу.
Глубина узла — это длина пути к его корню.
Справочник терминов
Бинарные деревья
Теперь рассмотрим особый тип деревьев, называемых бинарными или двоичными деревьями.
“В информатике бинарным (двоичным) деревом называется иерархическая структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.” — Wikipedia
Рассмотрим пример бинарного дерева.
Давайте закодируем бинарное дерево
Как мы реализуем простое двоичное дерево, которое инициализирует эти три свойства?
Вот наш двоичный класс дерева.
Когда мы создаем наш узел, он не имеет потомков. Просто есть данные узла.
Давайте это проверим:
Перейдем к части вставки. Что нам нужно здесь сделать?
Мы реализуем метод вставки нового узла справа и слева.
Давайте это нарисуем 🙂
Вот программный код:
Еще раз, если текущий узел не имеет левого дочернего элемента, мы просто создаем новый узел и устанавливаем его в качестве left_child текущего узла. Или мы создаем новый узел и помещаем его вместо текущего левого потомка. Назначим этот левый дочерний узел в качестве левого дочернего элемента нового узла.
И мы делаем то же самое, чтобы вставить правый дочерний узел.
Но не полностью. Осталось протестировать.
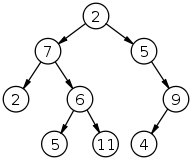
Давайте построим следующее дерево:
Подытоживая изображенное дерево, заметим:
Таким образом, вот код для нашего дерева следующий:
Теперь нам нужно подумать об обходе дерева.
У нас есть два варианта: поиск в глубину (DFS) и поиск по ширине (BFS).
• Поиск в глубину (Depth-first search, DFS) — один из методов обхода дерева. Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» дерева, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в не рассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из не рассмотренных вершин.
• Поиск в ширину (breadth-first search, BFS) — метод обхода дерева и поиска пути. Поиск в ширину является одним из неинформированных алгоритмов поиска. Поиск в ширину работает путём последовательного просмотра отдельных уровней дерева, начиная с узла-источника. Рассмотрим все рёбра, выходящие из узла. Если очередной узел является целевым узлом, то поиск завершается; в противном случае узел добавляется в очередь. После того, как будут проверены все рёбра, выходящие из узла, из очереди извлекается следующий узел, и процесс повторяется.
Давайте подробно рассмотрим каждый из алгоритмов обхода.
Поиск в глубину (DFS)
DFS исследует все возможные пути вплоть до некоторого листа дерева, возвращается и исследует другой путь (осуществляя, таким образом, поиск с возвратом). Давайте посмотрим на пример с этим типом обхода.
Результатом этого алгоритма будет: 1–2–3–4–5–6–7.
Давайте разъясним это подробно.
Проход в глубь дерева, а затем возврат к исходной точке называется алгоритмом DFS.
После знакомства с этим алгоритмом обхода, рассмотрим различные типы DFS-алгоритма: предварительный обход (pre-order), симметричный обход (in-order) и обход в обратном порядке (post-order).
Предварительный обход
Именно это мы и делали в вышеприведенном примере.
1. Записать значение узла.
2. Перейти к левому потомку и записать его. Это выполняется тогда и только тогда, когда имеется левый потомок.
3. Перейти к правому потомку и записать его. Это выполняется тогда и только тогда, когда имеется правый потомок.
Что такое дерево ?Моделями каких систем могут служить деревья ?Приведите пример такой системы
Дерево — это граф, в котором нет циклов, т. е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
Всякая иерархическая система может быть представлена с помощью дерева.
У дерева выделяется одна главная вершина, называемая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный предком объект входит в один класс (класс — множество объектов, обладающих общими признаками.) высшего уровня.
Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не имеющие порождённых вершин, называются листьями.
Родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.
3.во всех, кроме новейших экспериментальных
4.11011 после последней 1 в правом нижнем углу цифра 2 — число в двоичной системе счисления.
94 после 4, в правом нижнем 10=136 после 6, в правом нижнем углу 8
9.Дополнительный код позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и без знаковых чисел, чем упрощает архитектуру ЭВМ.
8.Прямой код числа кодирует только знаковую информацию и используется для хранения положительных и отрицательных чисел в ЭВМ.
Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение.
Какой граф называется деревом? Что такое дерево в информатике?
Содержание:
Граф-дерево является очень распространенным видом графов в информатике. Они нужны для хранения какой-либо информации в нелинейной структуре в иерархическом порядке.
Граф — это структура, состоящая из множества вершин, соединенных ребрами. Все в своей жизни видели транспортные схемы (передвижение автобусов или метро). Если эти схемы смоделировать в компьютере, то остановки и станции — это будут вершины графа, а маршрут транспорта между остановками/станциями — ребра графа.
В зависимости от того, каким образом расположены вершины, какое отношение между ними и каким способом они соединяются между собой ребрами, различают различные виды графов. Граф-дерево — это всего лишь один из множества видов графов.
Граф-дерево
Самое главное, все имена вы соединяли линиями зависимости между собой. Например, свое имя соединили с именами братьев и сестер и с именами своих родителей. Имена ваших родителей вы соединили с именами их братьев и сестер и с их родителями и т. д.
В информатике, граф-дерево выглядит точно так же, как и ваше генеалогическое дерево, только вместо имен — вершины, а вместо линий, связывающих имена — ребра.
Охарактеризовать граф-дерево в информатике можно так — это связный граф, где между двумя вершинам есть единственный связный путь. Вернемся к нашему дереву. Ваше имя будет связано линиями только с вашими родителями и вашими братьями/сестрами, с другими именами дерева у вас нет прямой связи. Например, с вашими дядями, тетями, бабушками и дедушками вы будете связаны только через ваших родителей, а не напрямую. А с вашей прабабушкой или вашим прадедушкой вы будете связаны только через родителей и бабушек с дедушками.
То есть граф-дерево в информатике следует строгой иерархии — одни элементы находятся «наверху» графа и будут называться «корнем дерева», другие элементы будут чуть ниже и будут называться «потомками», от «потомков» будут исходить «листья» — это те вершины, которые не имеют «потомков». Любой элемент верхнего уровня по отношению к нижнему уровню будет называться «предком».
Вернемся к нашему генеалогическому дереву. Бабушка с дедушкой (или прабабушка с прадедушкой, то есть в зависимости до какой глубины своих предков вы дойдете) будут корнем вашего граф-дерева (либо подкорнем, если у вас в корне будут прабабушка с прадедушкой). Ваши родители — это «потомки» вашего граф-дерева и бабушка с дедушкой для них будут «предками» вашего дерева. Вы будете «листьями» граф-дерева, потому что у вас пока нет своего потомства, как только у вас появятся дети, то вы станете «потомками» графа, а ваши дети «листьями». Ваши родители для вас будут «предками» графа.
Дерево (структура данных)
Дерево — одна из наиболее широко распространённых структур данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов. Является связанным графом, не содержащим циклы. Большинство источников также добавляют условие на то, что рёбра графа не должны быть ориентированными. В дополнение к этим трём ограничениям, в некоторых источниках указываются, что рёбра графа не должны быть взвешенными.
Содержание
Определения
Дерево считается ориентированным, если в корень не заходит ни одно ребро.
Узел является экземпляром одного из двух типов элементов графа, соответствующим объекту некоторой фиксированной природы. Узел может содержать значение, состояние или представление отдельной информационной структуры или самого дерева. Каждый узел дерева имеет ноль или более узлов-потомков, которые располагаются ниже по дереву (по соглашению, деревья ‘растут’ вниз, а не вверх, как это происходит с настоящими деревьями). Узел, имеющий потомка, называется узлом-родителем относительно своего потомка (или узлом-предшественником, или старшим). Каждый узел имеет не больше одного предка. Высота узла — это максимальная длина нисходящего пути от этого узла к самому нижнему узлу (краевому узлу), называемому листом. Высота корневого узла равна высоте всего дерева. Глубина вложенности узла равна длине пути до корневого узла.
Корневые узлы
Самый верхний узел дерева называется корневым узлом. Быть самым верхним узлом подразумевает отсутствие у корневого узла предков. Это узел, на котором начинается выполнение большинства операций над деревом (хотя некоторые алгоритмы начинают выполнение с «листов» и выполняются, пока не достигнут корня). Все прочие узлы могут быть достигнуты путём перехода от корневого узла по рёбрам (или ссылкам). (Согласно формальному определению, каждый подобный путь должен быть уникальным). В диаграммах он обычно изображается на самой вершине. В некоторых деревьях, например, кучах, корневой узел обладает особыми свойствами. Каждый узел дерева можно рассматривать как корневой узел поддерева, «растущего» из этого узла.
Поддеревья
Поддерево — часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева. Любой узел дерева T вместе со всеми его узлами-потомками является поддеревом дерева T. Для любого узла поддерева либо должен быть путь в корневой узел этого поддерева, либо сам узел должен являться корневым. То есть поддерево связано с корневым узлом целым деревом, а отношения поддерева со всеми прочими узлами определяются через понятие соответствующее поддерево (по аналогии с термином «соответствующее подмножество»).
Упорядочивание деревьев
Существует два основных типа деревьев. В рекурсивном дереве или неупорядоченном дереве имеет значение лишь структура самого дерева без учёта порядка потомков для каждого узла. Дерево, в котором задан порядок (например, каждому ребру, ведущему к потомку, присвоены различные натуральные числа) называется деревом с именованными рёбрами или упорядоченным деревом со структурой данных, заданной перед именованием и называемой структурой данных упорядоченного дерева.
Упорядоченные деревья являются наиболее распространёнными среди древовидных структур. Двоичное дерево поиска — одно из разновидностей упорядоченного дерева.
Представление деревьев
Существует множество различных способов представления деревьев. Наиболее общий способ представления изображает узлы как записи, расположенные в динамически выделяемой памяти с указателями на своих потомков, предков (или и тех и других), или как элементы массива, связанные между собой отношениями, определёнными их позициями в массиве (например, двоичная куча).
Деревья как графы
В теории графов дерево — связанный ациклический граф. Корневое дерево — это граф с вершиной, выделенной в качестве корневой. В этом случае любые две вершины, связанные ребром, наследуют отношения «родитель-потомок». Ациклический граф со множеством связанных компонентов или набор корневых деревьев иногда называется лесом.
Методы обхода
Пошаговый перебор элементов дерева по связям между узлами-предками и узлами-потомками называется обходом дерева. Зачастую, операция может быть выполнена переходом указателя по отдельным узлам. Обход, при котором каждый узел-предок просматривается прежде его потомков называется предупорядоченным обходом или обходом в прямом порядке (pre-order walk), а когда просматриваются сначала потомки, а потом предки, то обход называется поступорядоченным обходом или обходом в обратном порядке (post-order walk). Существует также симметричный обход, при котором посещается сначала левое поддерево, затем узел, затем — правое поддерево, и обход в ширину, при котором узлы посещаются уровень за уровнем (N-й уровень дерева — множество узлов с высотой N). Каждый уровень обходится слева направо.
Содержание урока
Что такое дерево?
Что такое дерево?
Как вы знаете из учебника 10 класса, дерево — это структура, отражающая иерархию (отношения подчинённости, многоуровневые связи). Напомним некоторые основные понятия, связанные с деревьями.
Дерево состоит из узлов и связей между ними (они называются дугами). Самый первый узел, расположенный на верхнем уровне (в него не входит ни одна стрелка-дуга), — это корень дерева. Конечные узлы, из которых не выходит ни одна дуга, называются листьями. Все остальные узлы, кроме корня и листьев, — это промежуточные узлы.
Из двух связанных узлов тот, который находится на более высоком уровне, называется родителем, а другой — сыном. Корень — это единственный узел, у которого нет родителя; у листьев нет сыновей.
Используются также понятия «предок» и «потомок». Потомок какого-то узла — это узел, в который можно перейти по стрелкам от узла-предка. Соответственно, предок какого-то узла — это узел, из которого можно перейти по стрелкам в данный узел.
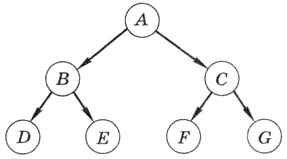
В дереве на рис. 6.11 родитель узла Е — это узел В, а предки узла Е — это узлы А и В, для которых узел Е — потомок. Потомками узла А (корня дерева) являются все остальные узлы.

Высота дерева, приведённого на рис. 6.11, равна 2.
Формально дерево можно определить следующим образом:
1) пустая структура — это дерево;
2) дерево — это корень и несколько связанных с ним отдельных (не связанных между собой) деревьев.
Здесь множество объектов (деревьев) определяется через само это множество на основе простого базового случая (пустого дерева). Такой приём называется рекурсией (см. главу 8 учебника для 10 класса). Согласно этому определению, дерево — это рекурсивная структура данных. Поэтому можно ожидать, что при работе с деревьями будут полезны рекурсивные алгоритмы.
Чаще всего в информатике используются двоичные (или бинарные) деревья, т. е. такие, в которых каждый узел имеет не более двух сыновей. Их также можно определить рекурсивно.

1) пустая структура — это двоичное дерево;
2) двоичное дерево — это корень и два связанных с ним отдельных двоичных дерева (левое и правое поддеревья).
Деревья широко применяются в следующих задачах:
• поиск в большом массиве неменяющихся данных;
• сортировка данных;
• вычисление арифметических выражений;
• оптимальное кодирование данных (метод сжатия Хаффмана).
Следующая страница 
Cкачать материалы урока