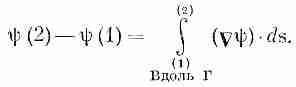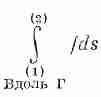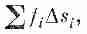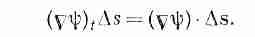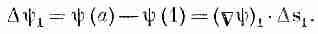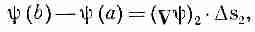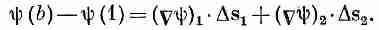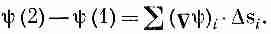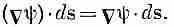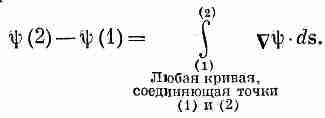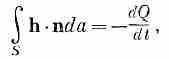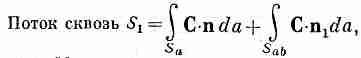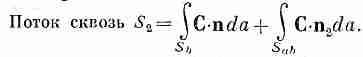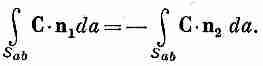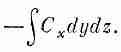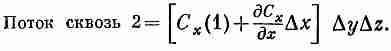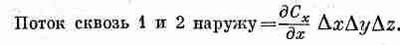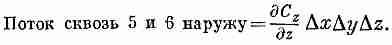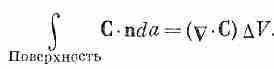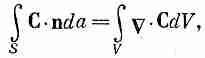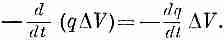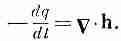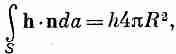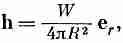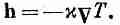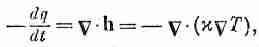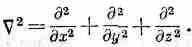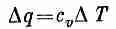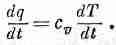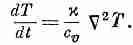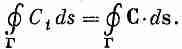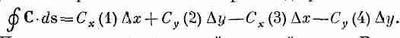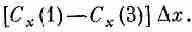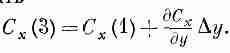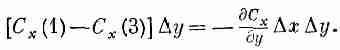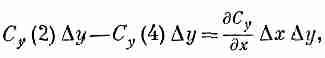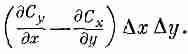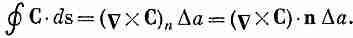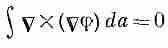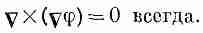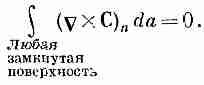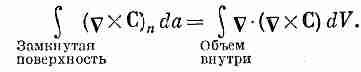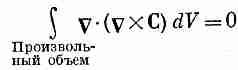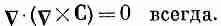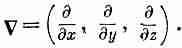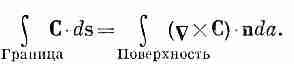Интеграл по контуру что это

Интеграл по контуру что это

До сих пор мы рассматривали криволинейный интеграл (1)

и изучали тот важный класс случаев, когда этот интеграл не зависит от пути интегрирования. Обратимся теперь к рассмотрению интеграла

взятого по любому простому замкнутому контуру в пределах области (D), и поставим вопрос об условиях, при которых этот интеграл всегда обращается в нуль. Оказывается, что этот вопрос совершенно эквивалентен вопросу, решенному выше: если при данном дифференциальном выражении (2) интеграл (1) не зависит от пути, то интеграл (9) всегда равен нулю, и обратно.

Действительно, предположим сначала независимость интеграла (1) от пути. Если есть любой простой замкнутый контур в области (D) (рис. 22), то произвольно взятыми на нем точками А и В разложим его на части (АМВ) и Так как интегралы по этим кривым должны быть равны:

Пусть теперь, обратно, дано, что интеграл (9) по простому замкнутому контуру всегда равен нулю. Взяв две точки А и В, соединим их двумя путями (АМВ) и из них составится замкнутый контур

Легким будет случай, когда линии (АМВ) и кроме точек А и В, общих точек не имеют; тогда контур сам себя не пересекает, т. е. оказывается простым.

Если же кривые (АМВ) и взаимно пересекаются, то замкнутая кривая уже не будет простой.

Однако, как показывает следующая лемма, можно все же ограничиться рассмотрением интегралов по простым (т. е. не пересекающим себя) замкнутым контурам.

Лемма. Если интеграл (9) равен нулю, по какому бы простому (т. е. не пересекающему себя) замкнутому контуру его ни взять, то он будет нулем и при всяком замкнутом контуре, хотя бы и самопересекающемся.

В силу леммы, установленной в п° 550, достаточно доказать это утверждение для любой замкнутой ломаной, хотя бы и самопересекающейся. Пусть (I) и будет такая ломаная, определенным образом направленная. Исходя из некоторой ее точки и следуя направлению ломаной, опишем часть ломаной до первого самопересечения — в точке Отбросив получившуюся замкнутую ломаную продолжим путь до нового самопересечения, что позволит выделить еще одну замкнутую ломаную (Ц), и т. д. После конечного числа шагов ломаная (I) окажется распавшейся на конечное число не пересекающих себя замкнутых ломаных

вдоль по которым интеграл заведомо нуль. Значит, он равен нулю и вдоль ломаной (I), что и требовалось доказать.

Таким образом, нами доказана полезная

Теорема 4. Для того чтобы криволинейный интеграл (1) не зависел от пути, необходимо и достаточно, чтобы интеграл (9) по любому замкнутому контуру был равен нулю. При этом условие остается достаточным и в том случае, если ограничиться лишь простыми (т. е. не пересекающими себя) замкнутыми контурами.

Теперь ясно, что об обращении в нуль интеграла (9) по замкнутому пути можно судить с помощью того же критерия, который в теореме 3 был установлен для независимости интеграла (1) от пути:

Теорема 5. Для того чтобы интеграл (9), по какому бы замкнутому контуру в пределах области (D) его ни взять, обращался в нуль, необходимо, а в случае односвязности области (D) и достаточно выполнение условия (А). Это условие остается необходимым и в том случае, если ограничиться лишь простыми (т. е. не пересекающими себя) замкнутыми контурами.

Ниже [601], располагая более развитым аппаратом (двойные интегралы, формула Грина), мы вернемся к вопросам, рассмотренным в настоящем параграфе, и некоторые из установленных здесь результатов получим вновь и притом более экономным образом.

Источник

Электронная библиотека

Если функция непрерывна на L, то интеграл существует (его часто называют контурным):

являются криволинейными интегралами от функций двух действительных переменных.

Если кривая L задана параметрическими уравнениями:

и каждая из этих функций гладкая, то

Известно, что вместо двух вещественных параметриче­ских уравнений линии L можно ввести одно эквивалентное им комплексно-параметрическое уравнение

тогда уравнение (2.35) можно переписать так:

Формула (2.36) удобна для вычисления контурных интегра­лов.

Теорема 1 (основная теорема Коши). Если функция f(z) аналитична в односвязной области, то для любого кусочно-гладкого замкнутого контура L, лежащего в этой области,

Следствие. Если функция f(z) аналитична в односвязной замкнутой области, ограниченной кривой L, то

Заметим, что из теоремы Коши следует: если функция f(z) аналитична в односвязной области D, то для любой незамк­нутой кривой L, принадлежащей D, интеграл от f(x) по L за­висит только от начальной точки z₀ и конечной точки z, т.е. от формы кривой (пути) L не зависит. При этом:

где F(z) – одна из первообразных функций для f(z), т.е. F’(z) = f(z). Формула (2.37) называется формулой Ньютона-Лейбница.

Теорема 2. Если функция f(z) аналитична в замкнутой области (односвязной или многосвязной) и L – граница D, то для любой точки z₀, лежащей внутри этой области, справедливы следую­щие формулы:

Интеграл в правой части формулы (2.39) называется интегралом Коши для функции f(z), а сама эта формула носит название инте­гральной формулы Коши.

Отметим, что формула (2.39) получается из интегральной формулы Коши (2.38) в результате последовательного дифференцирования n раз по z₀ под знаком интеграла.

Вычислить контурный интеграл где L – прямолинейный отрезок, соединяю­щий точку z = 0 с точкой z = 3+7i.

1) Сделаем схематический рисунок пути (контура) ин­тегрирования (рис. 2.3).

2) Составим параметрические уравнения или комплекс­но-параметрическое уравнение пути (контура) интегрирования. Если путь интегрирования состоит из прямолиней­ных участков, то целесообразно использовать формулу для пря­мой, проходящей через две заданные точки:

Из условия z = 0, следует, что

из условия z = 3+7i, следует, что

3) Установим, как изменяется параметр t при движении от точки z = 0 до точки z = 3 + 7i.

При z = 0 у нас х = 0 и у = 0, а значит, из параметрических уравнений t = 0; при z = 3 + 7i имеем x = 3 и у = 7, тогда из тех же уравнений находим t = 1.

Если путь интегрирования состоит из двух отрезков, то составляются параметрические уравнения для каждого участка отдельно и находятся два интеграла.

Построить область, заданную на комплексной плоскости

Запишем область в другом виде с учетом, что получим:

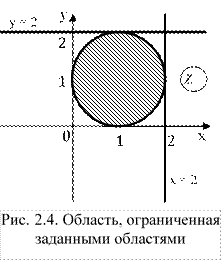
Это область, ограниченная окружностью с центром в точке (1, 1) и радиусом 1.

Ограничение запишем в виде:

Ограничение имеет вид:

Получили область, ограниченную графиками:

Изобразим область на графике (рис. 2.4). Заданная область заштрихована.

Найти интеграл от функции комплексного переменного, используя основную теорему Коши:

.

1) Построим область интегрирования:

Получили уравнение окружности с центром в точке О и радиусом (рис. 2.5).

2) Найдем точки и изобразим их на рисунке 2.5.

Из формулы (2.38) следует, что

1) Определяем интеграл, используя формулу (2.38):

Решение

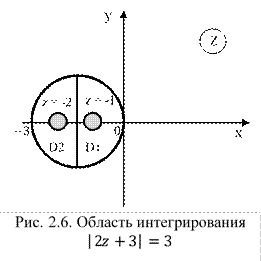
1) Построим область интегрирования:

Получили уравнение окружности с центром в точке О и радиусом (рис. 2.6).

2) Найдем точки и изобразим их на рисунке 2.6.

Из формулы (2.38) следует, что

Обе точки лежат в области интегрирования, следовательно, разбиваем область интегрирования на две замкнутые области D1 и D2. Интеграл разбиваем на два:

3) Определяем интегралы, используя формулу (2.38), найдем интеграл по области D1, где :

Найдем интеграл по области D2, где :

Складываем полученные интегралы и получаем:

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Источник

Глава 3 ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ВЕКТОРОВ

Глава 3

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ВЕКТОРОВ

§2.Поток векторного поля

§З. Поток из куба; теорема Гаусса

§4.Теплопроводность; уравнение диффу­зии

§5.Циркуляция векторного поля

§6. Циркуляция по квадрату; теорема Стокса

§7. Поля без роторов и поля без дивер­генций

§8.Итоги

§ 1. Векторные интегралы;

криволинейный интеграл от Сш

В предыдущей главе мы видели, что брать производные от поля можно по-разному. Одни приводят к векторным полям; другие — к скалярным. Хотя формул было выведено до­вольно много, все их можно подытожить одним правилом: операторы д/дх, д/ду и д/dz суть три компоненты векторного оператора у. Сейчас нам хотелось бы лучше разобраться в значении производных поля. Тогда мы легче почувствуем смысл векторных уравнений поля.

Мы уже говорили о смысле операции градиен­та (С на скаляр). Обратимся теперь к смыслу опе­раций вычисления дивергенции (расходимости) и ротора (вихря). Толкование этих величин лучше всего сделать на языке векторных интегралов и уравнений, связывающих эти интегралы. Но уравнения эти, к несчастью, нельзя вывести из векторной алгебры при помощи каких-либо легких подстановок, так что вам придется учить их как что-то новое. Одна из этих инте­гральных формул практически тривиальна, а другие две — нет. Мы выведем их и поясним их смысл. Эти формулы фактически являются математическими теоремами. Они полезны не только для толкования смысла и содержания понятий дивергенции и ротора, но и при раз­работке общих физических теорий. Для теории полей эти математические теоремы — все равно, что теорема о сохранении энергии для меха­ники частиц. Подобные теоремы общего харак­тера очень важны для более глубокого пони­мания физики. Но вы увидите, что, за немногими простыми исключениями, они мало что дают для решения задач. К счастью, как

раз в начале нашего курса многие простые задачи будут решаться именно этими тремя интегральными формулами.

Фиг. 3.1. Иллюстрация уравнения (3.1).

Вектор Сш вычисляется на линей­ном элементе ds.

Позже, однако, когда задачи станут потруднее, этими простыми методами мы больше обойтись не сможем.

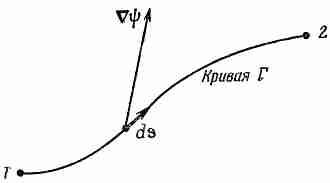
Мы начнем с той интегральной формулы, куда входит гра­диент. Мысль, которая содержится в ней, очень проста: раз градиент есть быстрота изменения величины поля, то интеграл от этой быстроты даст нам общее изменение поля. Пусть у нас есть скалярное поле ш(x, у, z). В двух произвольных точках (1) и (2) функция я|з имеет соответственно значения ш(l) и ш(2). [Используется такое удобное обозначение: (2) означает точку (x 2, y 2, z 2), а ш(2) это то же самое, что ш(x 2, y 2, z 2).] Если Г (гамма) — произвольная кривая, соединяющая (1) и (2) (фиг. 3.1), то справедлива

Интеграл, стоящий здесь, это криволинейный интеграл от (1) до (2) вдоль кривой Г от скалярного произведения вектора Сш) на другой вектор, ds, являющийся бесконечно малым элемен­том дуги кривой Г [направленной от (1) к (2)].

подразумевается предел суммы

где f i — значение функции где-то на i-й хорде. Предел — это то,

Фиг. 3.2. Криволинейный интег­рал есть предел суммы.

к чему стремится сумма, когда растет число хорд (разумным об­разом, чтобы даже наибольшее Ds i®0).

В нашей теореме (3.1) интеграл означает то же самое, хоть и выглядит чуть по-иному. Вместо f стоит другой скаляр — составляющая Сш в направлении Ds. Если обозначить эту составляющую через (Сш) t , то ясно, что

Интеграл в (3.1) и подразумевает сумму таких членов.

А теперь посмотрим, почему уравнение (3.1) правильно. В гл. 1 мы показали, что составляющая Сш вдоль малого сме­щения DR равна быстроте изменения ш в направлении DR. Рассмотрим хорду кривой Ds от точки (1) до точки а на фиг. 3.2. По нашему определению

Точно так же мы имеем

где, конечно, (Сш) 1 означает градиент, вычисленный на хорде Ds 1, a (Сш) 2 — градиент, вычисленный на Ds 2. Сложив (3.3) и (3.4), получим

Вы видите, что, продолжая прибавлять такие члены, мы полу­чаем в итоге

Левая часть не зависит от того, как выбирать интервалы — лишь бы точки (1) и (2) были теми же самыми, так что справа можно перейти к пределу. Так доказывается уравнение (3.1). Из нашего доказательства видно, что, подобно тому как ра­венство не зависит и от выбора точек а, b, с. точно так же оно не зависит от выбора самой кривой Г. Теорема верна для любой кривой, соединяющей точки (1) и (2).

Два слова об обозначениях. Не будет путаницы, если писать для удобства

Тогда наша теорема примет такой вид:

§ 2. Поток векторного поля

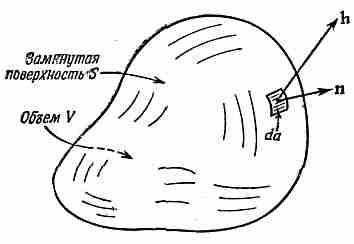
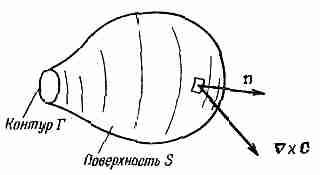
Прежде чем рассматривать следующую интегральную теоре­му — теорему о дивергенции,— хотелось бы разобраться в од­ной идее, смысл которой в случае теплового потока легко усваи­вается. Мы уже определили вектор h, представляющий коли­чество тепла, протекающего сквозь единицу площади в еди­ницу времени. Положим, что внутри тела имеется замкнутая поверхность S, ограничивающая объем V (фиг. 3.3). Нам хочется узнать, сколько тепла вытекает из этого объема. Мы это можем, конечно, определить, рассчитав общий тепловой поток через поверхность S.

Обозначим через da площадь элемента поверхности. Этот символ заменяет двумерный дифференциал. Если, например, элемент окажется в плоскости ху, то

Позже мы будем иметь дело с интегралами по объему, и тогда будет удобно рассматривать элемент объема в виде малого куби­ка и обозначать его dV, подразумевая, что

Кое-кто пишет и d 2 a вместо da, чтобы напомнить самому себе, что это выражение второй степени; вместо dV пишут также d 3 V. Мы будем пользоваться более простыми обозначениями, а вы уж постарайтесь не забывать, что у площадей бывают два измерения, у объемов — три.

Фиг. 3.3. Замкнутая поверх­ность S, ограничивающая объем V.

Единичный вектор n — внешняя нор­маль к элементу поверхности da, a h — вектор теплового потопа сквозь элемент поверхности.

Поток тепла через элемент поверхности da равен произведе­нию площади на составляющую h, перпендикулярную к da. Мы уже определяли n — единичный вектор, направленный наружу перпендикулярно к поверхности (см. фиг. 3.3). Искомая составляющая h равна

и тогда поток тепла сквозь da равен

А весь поток тепла через произвольную поверхность получается суммированием вкладов от всех элементов поверхности. Иными словами, (3.10) интегрируется по всей поверхности

Этот интеграл мы будем называть «поток h через поверх­ность». Мы рассматриваем h как «плотность потока» тепла, а поверхностный интеграл от h — это общий поток тепла наружу через поверхность, т. е. тепловая энергия за единицу времени (джоули в секунду).

Мы хотим эту идею обобщить на случай, когда вектор не представляет собой потока какой-то величины, а, скажем, является электрическим полем. Конечно, если это будет нужно, то и в этом случае все равно можно проинтегрировать нормаль­ную составляющую электрического поля по площади. Хотя теперь она уже не будет ничьим потоком, мы все еще будем упот­реблять слово

«поток». Мы будем говорить, что

Слову «поток» мы придаем смысл «поверхностного интеграла от нормальной составляющей» некоторого вектора. То же опре­деление будет применяться и тогда, когда поверхность незамк­нута.

А возвращаясь к частному случаю потока тепла, обратим внимание на те случаи, когда количество тепла сохраняется. Представьте себе, к примеру, материал, в котором после перво­начального подогрева не происходит ни дальнейшего подвода, ни поглощения тепла. Тогда, если из какой-то замкнутой по­верхности наружу поступает тепло, содержание тепла во внут­реннем объеме должно падать. Так что в условиях, когда количество тепла сохраняется, мы говорим, что

где Q — запас тепла внутри S. Поток тепла из S наружу равен со знаком минус быстроте изменения со временем общего за­паса тепла Q внутри S. Это толкование возможно оттого, что речь идет о потоке тепла, и оттого, что мы предположили, что количество тепла сохраняется. Конечно, если бы внутри объема создавалось тепло, нельзя было бы говорить о полном запасе тепла в нем.

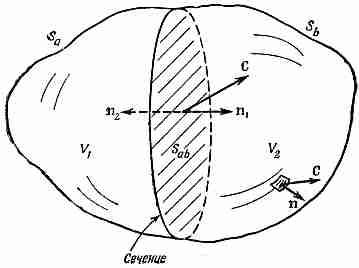
Укажем теперь на интересное свойство потока любого век­тора. Можете при этом представлять себе вектор потока тепла, но верно это будет и для произвольного векторного поля С. Представьте себе замкнутую поверхность S, окружающую объем V. Разобьем теперь объем на две части каким-то «сече­нием» (фиг. 3.4). Получились два объема и две замкнутые по­верхности. Объем V 1окружен поверхностью S 1 , составленной частью из прежней поверхности S aи частью из «сечения» S ab. Объем V 2 окружен поверхностью S 2, составленной из остатка прежней поверхности (S b) и замкнутой сечением S ab. Зададим вопрос: если мы рассчитаем поток через поверхность S lи при­бавим к нему поток сквозь поверхность S 2, будет ли их сумма равна потоку через первоначальную поверхность? Ответ гласит: «Да». Потоки через часть S ab , общую обеим поверхностям S 1 и S 2, в точности сократятся. Для потока вектора С из V 1можно написать

а для потока из V 2:

Заметьте, что во втором интеграле мы обозначили внешнюю нормаль к S abбуквой n 1, если она относится к S 1 , и буквой n 2, если она относится к S 1(см. фиг. 3.4).

Ясно, что n 1=-n 2, и тем

Складывая теперь уравнения (3.14) и (3.15), мы убеждаемся, что сумма потоков сквозь S 1и S 2как раз равна сумме двух ин­тегралов, которые, взятые вместе, дают поток через перво­начальную поверхность S=S a+S b.

Мы видим, что поток через всю внешнюю поверхность S можно рассматривать как сумму потоков из тех двух частей, на которые разрезан объем. Эти части можно еще разрезать: скажем, V 1разбить пополам. Опять придется прибегнуть к тем же доводам. Так что для любого способа разбиения первоначаль­ного объема всегда остается справедливым то свойство, что по­ток через внешнюю поверхность (первоначальный интеграл) равен сумме потоков изо всех внутренних частей.

§ 3. Поток из куба; теорема Гаусса

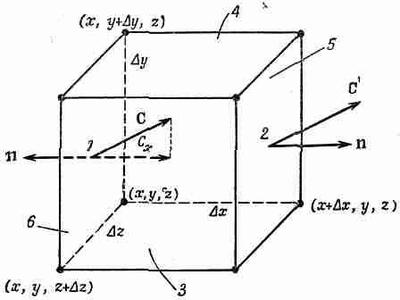
Рассмотрим теперь частный случай потока из маленького ку­бика и получим интересную формулу. Ребра куба пусть нап­равлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у, z, ребро куба в направлении х равно Dx, ребро куба (а точнее, бруска) в направлении у равно Dy, а в направлении z равно Dz. Мы хотим найти поток вектор­ного поля С через поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5).

Поток наружу сквозь нее равен x-компоненте С с минусом, проинтегрированной по площади грани. Он равен

Так как куб считается малым, этот интеграл можно заменить значением С х в центре грани 1эту точку мы обозначили (1), умноженным на площадь грани DyDz:

Поток сквозь 1 наружу=-C x(1)DyDz.

Подобным же образом поток наружу через грань 2 равен

Поток сквозь 2 наружу= C x(2) DyDz.

Фиг. 3.5. Вычисление потока вектора С из маленького кубика.

Величины C x(1) и С х(2), вообще говоря, слегка отличаются. Ес­ли Dх достаточно мало, то можно написать

Существуют, конечно, и другие члены, но в них входит (Dx) 2 и высшие степени Dx, и в пределе малых Dx ими запросто можно пренебречь. Значит, поток сквозь грань 2 равен

Складывая потоки через грани 1 и 2, получаем

Производную нужно вычислять в центре грани 1, т. е. в точке [x, y+(Dy/2), z+(Dz/2)]. Но если куб очень маленький, мы сде­лаем пренебрежимую ошибку, если вычислим ее в вершине (х, у, z).

Повторяя те же рассуждения с каждой парой граней, мы получаем

А общий поток через все грани равен сумме этих членов. Мы обнаруживаем, что

Сумма производных в скобках как раз есть С·С, a DxDyDz=DV (объем куба). Таким образом, мы можем утверждать, что для бесконечно малого куба

Мы показали, что поток наружу с поверхности бесконечно ма­лого куба равен произведению дивергенции вектора на объем куба. Теперь мы понимаем «смысл» понятия дивергенции век­тора. Дивергенция вектора в точке Р — это поток С («исте­чение» С наружу) на единицу объема, взятого в окрестности Р. Мы связали дивергенцию С с потоком С из бесконечно малого объема. Для любого конечного объема можно теперь использовать факт, доказанный выше, что суммарный поток из объема есть сумма потоков из отдельных его частей. Иначе говоря, мы можем проинтегрировать дивергенцию по всему объему. Это приводит нас к теореме, согласно которой интеграл от нормальной составляющей произвольного вектора по замк­нутой поверхности может быть представлен также в виде ин­теграла от дивергенции вектора по объему, заключенному внутри поверхности. Теорему эту называют теоремой Гаусса.

где S — произвольная замкнутая поверхность, V — объем внутри нее.

§ 4, Теплопроводность; уравнение диффузии

Чтобы привыкнуть к теореме, разберем на примере, как ее применяют. Обратимся опять к распространению тепла, скажем в металле, рассмотрим совсем простой случай: все тепло было подведено к телу заранее, а теперь тело остывает. Источников теп­ла нет, так что количество тепла сохраняется. Сколько же тогда тепла должно оказаться внутри некоего определенного объема в какой-то момент времени? Оно должно уменьшаться как раз на то количество, которое уходит с поверхности объема. Если этот объем — маленький кубик, то,

следуя формуле (3.17), мож­но написать

Но это должно быть равно скорости потери тепла внутренностью куба. Если q — количество тепла в единице объема, то весь

запас тепла в кубе qDV, а скорость потерь равна

Сравнивая (3.19) с (3.20), мы видим, что

Внимательно вглядитесь в форму этого уравнения; эта форма часто встречается в физике. Она выражает закон сохра­нения, в данном случае закон сохранения тепла. В уравнении (3.13) тот же физический факт был выражен иначе. Там была интегральная форма уравнения сохранения, а здесь у нас — дифференциальная форма.

Уравнение (3.21) мы получили, применив формулу (3.13) к бесконечно малому кубу. Можно пойти и по другому пути. Для большого объема F, ограниченного поверхностью S, за­кон Гаусса утверждает, что

Теперь рассмотрим другой случай. Представим, что в блоке вещества имеется маленькая дырочка, а в ней идет химическая реакция, генерирующая тепло. Можно еще представить себе, что к маленькому сопротивлению внутри блока подведены про­волочки, нагревающие его электрическим током. Предположим, что тепло создается практически в одной точке, a W представ­ляет собой энергию, возникающую в этой точке за секунду. В остальной же части объема пусть тепло сохраняется и, кро­ме того, пусть генерация тепла началась так давно, что сейчас температура уже нигде больше не изменяется. Вопрос состоит в следующем: как выглядит вектор потока тепла h в разных точках металла? Сколько тепла перетекает через каждую точку?

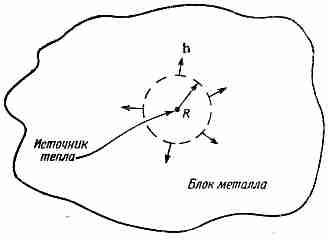
Мы знаем, что если мы будем интегрировать нормальную составляющую h по замкнутой поверхности, окружающей источ­ник, то всегда получится W. Все тепло, которое генерируется в точечном источнике, должно протечь через поверхность, ибо предполагается, что поток постоянен. Перед нами трудная задача отыскания такого векторного поля, которое после ин­тегрирования по произвольной поверхности всегда давало бы W. Но мы сравнительно легко можем найти это поле, выбрав поверхность специального вида. Возьмем сферу радиусом R с центром в источнике и предположим, что поток тепла радиален (фиг. 3.6). Интуиция нам подсказывает, что h должен быть направлен по радиусу, если блок вещества велик и мы не приближаемся слишком близко к его границам; кроме того, вели­чина h во всех точках сферы должна быть одинакова.

Фиг. 3.6. В области близ точеч­ного источника поток тепла на­правлен по радиусу наружу.

Вы ви­дите, что для получения ответа к нашим выкладкам мы вы­нуждены добавить известное количество домыслов (обычно это именуют «физической интуицией»).

где h — абсолютная величина h. Этот интеграл должен быть равен W — скорости, с которой источник генерирует тепло. Получается

где, как всегда, e r обозначает единичный вектор в радиаль­ном направлении. Этот результат говорит нам, что h пропорцио­нален W и меняется обратно квадрату расстояния от источника.

Только что полученный результат применим к потоку те­пла вблизи точечного источника тепла. Теперь попытаемся найти уравнения, которые справедливы для теплового потока самого общего вида (придерживаясь единственного условия, что количество тепла должно сохраняться). Нас будет интере­совать только то, что происходит в местах вне каких-либо ис­точников или поглотителей тепла.

Дифференциальное уравнение распространения тепла было получено в гл. 2. В соответствии с уравнением (2.44),

(Помните, что это соотношение приближенное, но для некоторых веществ вроде металлов выдерживается неплохо.) Применимо оно, конечно, только в тех частях тела, где нет ни выделения, ни поглощения тепла. Выше мы вывели другое соотношение (3.21), которое выполняется тогда, когда количество тепла сохраняется. Если мы это уравнение скомбинируем с (3.25), то получим

если c — величина постоянная. Напоминаю, что q — это количество тепла в единичном объеме, а С·С = С 2 — лапласиан, т. е. оператор

Если мы теперь сделаем еще одно допущение, сразу воз­никнет одно очень интересное уравнение. Допустим, что тем­пература материала пропорциональна содержанию тепла в еди­нице объема, т. е. что у материала есть определенная удельная теплоемкость. Когда это допущение верно (а так бывает часто), мы можем писать

Скорость изменения количества тепла пропорциональна ско­рости изменения температуры. Коэффициент пропорциональ­ности c vздесь — удельная теплоемкость на единицу объема материала. Подставляя (3.27) в (3.26), получаем

Мы обнаружили, что быстрота изменения со временем темпера­туры Т в каждой точке пропорциональна лапласиану от Т, т. е. вторым производным от пространственного распределения тем­ператур. Мы имеем дифференциальное уравнение — в перемен­ных х, у, z и t — для температуры Т.

Дифференциальное уравнение (3.28) называется уравнением диффузии тепла, или уравнением теплопроводности. Часто его пишут в виде

где D — постоянная. Она равна x/c v.

Уравнение диффузии появляется во многих физических задачах: о диффузии газов, диффузии нейтронов и других. Мы уже обсуждали физику некоторых таких явлений в вып. 4, гл. 43. Теперь перед вами полное уравнение, описывающее диффузию в самом общем виде. Немного позже мы зай­мемся решением уравнения диффузии, чтобы посмотреть, как распределяется температура в некоторых случаях. А сейчас вернемся к рассмотрению других теорем о векторных полях.

§ 5. Циркуляция векторного поля

Мы хотим теперь рассмотреть ротор поля примерно так же, как рассматривали дивергенцию. Мы вывели теорему Гаусса, вычисляя интеграл по поверхности, хотя с самого начала отнюдь не было ясно, что мы будем иметь дело с дивергенцией. Откуда же можно было знать, что для ее получения надо интегрировать по поверхности? Этот результат вовсе не был очевиден. И столь же неоправданно мы сейчас вычислим другую характе­ристику поля и покажем, что она связана с ротором. На этот раз мы подсчитаем так называемую циркуляцию векторного поля. Если С — произвольное векторное поле, мы возьмем его составляющую вдоль кривой линии и проинтегрируем эту составляющую по замкнутому контуру. Интеграл называется циркуляцией векторного поля по контуру. Мы уже раньше в этой главе рассматривали криволинейный интеграл от Сy. Сейчас мы то же самое проделываем с произвольным векторным полем С.

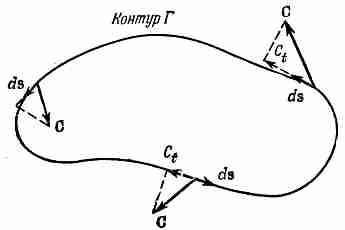
Пусть Г — произвольный замкнутый контур в пространстве (воображаемый, разумеется). Пример мы видим на фиг. 3.7. Криволинейный интеграл от касательной составляющей С по контуру записывается в виде

Фиг. 3.7. Циркуляция вектора С но кривой Г есть криволиней­ный интеграл от С t (касатель­ной составляющей С).

Заметьте, что интеграл берется по всему замкнутому пути, а не от одной точки до другой, как это делалось раньше. Кру­жочек на знаке интеграла должен нам напоминать об этом. Такой интеграл называется циркуляцией векторного поля по кривой Г. Название связано с тем, что первоначально так рас­считывали циркуляцию жидкости. Но название это, как и по­ток, было распространено на любые поля, даже такие, в которых «циркулировать» нечему.

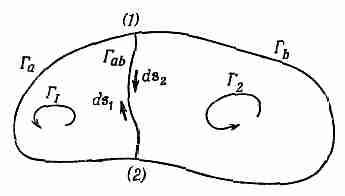
Забавляясь той же игрой, как с потоком, мы можем пока­зать, что циркуляция вдоль контура есть сумма циркуляции вдоль двух меньших контуров. Положим, что, соединив две точки (1) и (2) первоначальной кривой с помощью некоторой линии, мы разбили кривую на два контура Г 1 и Г 2 (фиг. 3.8). Контур Г 1 состоит из Г a — части первоначальной кривой слева от (1) и (2) и «соединения» Г ab . Контур Г 2 состоит из остатка первоначальной кривой плюс то же соединение.

Циркуляция вдоль Г 1 есть сумма интеграла вдоль Г а и вдоль Г аЬ. Точно так же и циркуляция вдоль Г 2 есть сумма двух ча­стей, одной вдоль Г b, другой — вдоль Г ab. Интеграл вдоль Г ab для кривой Г 2 имеет знак, противоположный тому знаку, кото­рый он имел для кривой Г 1 , потому что направления обхода противоположны (в обоих криволинейных интегралах направ­ления поворота нужно брать одни и те же).

Повторяя прежние аргументы, мы можем убедиться, что сумма двух циркуляции даст как раз криволинейный интеграл вдоль первоначальной кривой Г. Интегралы по Г ab сократятся. Циркуляция по одной части плюс циркуляция вдоль другой равняется циркуляции вдоль внешней линии. Этот процесс раз­резания большого контура на меньшие можно продолжить. При сложении циркуляции по меньшим контурам смежные части будут сокращаться, так что сумма их сведется к цирку­ляции вдоль единственного первоначального контура.

Теперь предположим, что первоначальный контур — это граница некоторой поверхности. Существует бесконечное мно­жество поверхностей, границей которых служит все тот же первоначальный замкнутый контур. Наши результаты не зави­сят, однако, от выбора этих поверхностей. Сперва мы разобьем наш первоначальный контур на множество малых контуров, лежащих на выбранной поверхности (фиг. 3.9).

Фиг. 3.9. Некоторая поверх­ность, ограниченная конту­ром Г.

Поверхность разделена на множе­ство маленьких участков, каждый примерно в форме квадрата. Цир­куляция по Г есть сумма циркуля­ции по всем маленьким контурам.

Какой бы ни была форма поверхности, но если малые контуры сделать до­статочно малыми, всегда можно будет считать каждый из них замыкающим достаточно плоскую поверхность. Кроме того, каждый из них можно сделать очень похожим на квадрат. И циркуляцию вокруг большого контура Г можно найти, под­считав циркуляции по всем квадратикам и сложив их.

§ 6. Циркуляция по квадрату; теорема Стокса

Как нам найти циркуляцию по каждому квадратику? Все зависит от того, как квадрат ориентирован в пространстве. Если ориентация его подобрана удачно (к примеру, он распо­ложен в одной из координатных плоскостей), то расчет сде­лать легко. Так как пока мы не делали никаких предположений об ориентации осей координат, мы вправе выбрать их так, чтобы тот квадратик, на котором мы сосредоточили свое вни­мание, оказался в плоскости ху (фиг. 3.10). Если результат расчета будет выражен в векторной записи, то можно говорить, что он не зависит от специальной ориентации плоскости.

Фиг. 3.10. Вычисление цирку­ляции вектора С по маленькому квадратику.

(3.31) Посмотрим теперь на первый и третий члены. В сумме они дают

Вам может показаться, что в принятом приближении эта раз­ность равна нулю. Но это только в первом приближении. Мы можем быть более точными и учесть скорость изменения С х , тогда можно написать

Производную при нашей точности можно брать в точке (х, у). Подобным же образом оставшиеся два члена можно написать в виде

и циркуляция по квадрату тогда равна

Интересно, что в скобках получилась как раз z-компонента ротора С. Множитель DxDy— это площадь нашего квадрата. Так что циркуляцию (3.36) можно записать как

Но z-компонента это на самом деле компонента, нормальная к элементу поверхности.

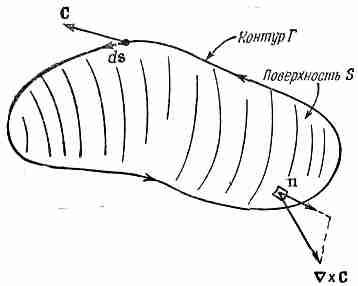
Фиг. 3.11. Циркуляция век­тора С по Г равна поверхност­ному интегралу от нормальной компоненты вектора СXС.

Поэтому циркуляцию вокруг квад­ратика можно задать и в инвариантной векторной записи:

В результате имеем: циркуляция произвольного вектора С по бесконечно малому квадрату равна произведению состав­ляющей ротора С, нормальной к поверхности, на площадь квад­рата.

Циркуляция по произвольному контуру Г легко теперь может быть увязана с ротором векторного поля. Натянем на кон­тур любую подходящую поверхность S (как на фиг. 3.11) и сложим между собой циркуляции по всем бесконечно малым квадратикам на этой поверхности. Сумма может быть записана в виде интеграла. В итоге получится очень полезная теорема, называемая теоремой Стокса [по имени физика Стокса].

где S — произвольная поверхность, ограниченная контуром Г. Теперь мы должны ввести соглашение о знаках. На приведен­ной ранее фиг. 3.10 ось z показывает на вас, если система коорди­нат «обычная», т. е. «правая». Когда в криволинейном интеграле мы брали «положительное» направление обхода, то циркуляция получилась равной z-компоненте вектора СXC. Обойди мы кон­тур в другую сторону, мы бы получили противоположный знак. Как вообще узнавать, какое направление надо выбирать для положительного направления «нормальной» компоненты век­тора СXC? «Положительную» нормаль надо всегда связывать с направлением так, как это сделано было на фиг. 3.10. Об­щий случай показан на фиг. 3.11.

Для запоминания годится «правило правой руки». Если вы расположите пальцы вашей правой руки вдоль контура Г, чтобы кончики пальцев показывали положительное направление обхода ds, то ваш большой палец укажет направление положи­тельной нормали к поверхности S.

§ 7. Поля без роторов и поля без дивергенций

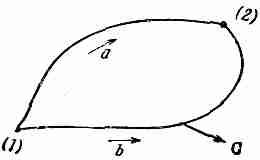
Теперь перейдем к некоторым следствиям из наших новых теорем. Возьмем сперва случай вектора, у которого ротор (или вихрь) повсюду равен нулю. Тогда, согласно теореме Стокса, циркуляция по любому контуру — нуль. Если мы теперь возь­мем две точки (1) и (2) на замкнутой кривой (фиг. 3.12), то кри­волинейный интеграл от касательной составляющей от (1) до (2) не должен зависеть от того, какой из двух возможных путей мы выбрали. Можно заключить, что интеграл от (1) до (2) может зависеть только от расположения этих точек, т. е. что он есть функция только от координат точек. Той же логикой мы пользо­вались в вып. 1, гл. 14, когда доказывали, что если интеграл от некоторой величины по произвольному замкнутому контуру всегда равен нулю, то этот интеграл может быть представлен в виде разности функций от координат двух концов. Это позво­лило нам изобрести понятие потенциала. Мы доказали далее, что векторное поле является градиентом этой потенциальной функ­ции [см. вып. 1, уравнение (14.13)].

Отсюда следует, что любое векторное поле, у которого ротор равен нулю, может быть представлено в виде градиента неко­торой скалярной функции, т. е. если АXС=0 всюду, то существует некоторая функция y (пси), для которой С = Сy (полезное представление). Значит, мы можем, если захотим, опи­сывать этот род векторных полей при помощи скалярных полей.

Теперь докажем еще одну формулу. Пусть у нас есть про­извольное скалярное поле j (фи). Если взять его градиент Сj, то интеграл от этого вектора по любому замкнутому контуру должен быть равен нулю.

Фиг. 3.12. Если СXС равно нулю, то циркуляция по замкнутой при­вой Г тоже нуль.

Криволинейный интеграл от C·ds на участке от (1) до (2) вдоль а должен быть равен интегралу вдоль b.

Фиг. 3.13. При переходе к пределу замкнутой поверхности поверхно­стный интеграл от (СXС) n должен обратиться в нуль.

Криволинейный интеграл от точки (1) до точки (2) равен [j(2)- j (1)]. Если точки (1) и (2) совпадают, то наша теорема 1 [уравнение (3.8)] сообщает нам, что криволинейный интеграл равен нулю:

Применяя теорему Стокса, можно заключить, что

по любой поверхности. Но раз интеграл по любой поверхности равен нулю, то подынтегральное выражение обязано быть равно нулю. Значит,

Тот же результат был доказан в гл. 2, § 7 при помощи векторной алгебры.

Рассмотрим теперь частный случай, когда на маленький контур Г натягивается большая поверхность S (фиг. 3.13). Мы хотим посмотреть, что случится, когда контур стянется в точку. Тогда граница поверхности исчезнет, а сама поверхность превратится в замкнутую. Если вектор С повсюду конечен, то криволинейный интеграл по Г должен стремиться к нулю по мере стягивания контура (интеграл в общем-то пропорционален длине контура Г, а она убывает). Согласно теореме Стокса, поверхност­ный интеграл от (СXС) n тоже должен убывать до нуля. Когда поверхность замыкается, то при этом каким-то образом в ин­теграл привносится вклад, который взаимно уничтожается с накопленным

ранее. Получается новая теорема:

Это нас должно заинтересовать, потому что у нас уже есть одна теорема о поверхностном интеграле векторного поля. Та­кой поверхностный интеграл равен объемному интегралу от дивергенции вектора, как это следует из теоремы Гаусса [уравнение (3.18)]. Теорема Гаусса в применении к СXС утверждает, что

Мы заключаем, что интеграл в правой части должен обращать­ся в нуль и что это должно быть справедливо для любого векторного по­ля С, каким бы оно ни было.

Раз уравнение (3.41) выполнено для произвольного объема, то в каждой точке пространства подын­тегральное выражение должно быть равно нулю. Получается, что

Тот же результат был выведен с помощью векторной алгебры в гл. 2, § 7. Теперь мы начинаем понимать, как все здесь прила­жено одно к другому.

§ 8. Итоги

Подытожим теперь все, что мы узнали о векторном исчисле­нии. Вот самые существенные моменты гл. 2 и 3.

1. Операторы д/дх, д/ду и д/dz можно рассматривать как три составляющих векторного оператора С; формулы, сле­дующие из векторной алгебры, остаются правильными, если этот оператор считать вектором

2. Разность значений скалярного поля в двух точках равна криволинейному интегралу от касательной составляющей гра­диента этого скаляра вдоль любой кривой, соединяющей пер­вую точку со второй:

Поверхностный интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности равен интег­ралу от дивергенции вектора по объему, лежащему внутри этой поверхности:

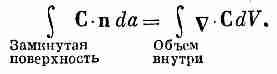
4. Криволинейный интеграл от касательной составляющей произвольного вектора по замкнутому контуру равен поверх­ностному интегралу от нормальной составляющей ротора этого вектора по произвольной поверхности, ограниченной этим кон­туром

От редактора. Начиная изучать уравнения Максвелла, обратите вни­мание, что в этих лекциях используется рационализированная система единиц, в которой уравнения Максвелла не содержат коэффициентов.

Более привычно вместо e 0 писать e 0/4p; тогда коэффициент 4p исче­зает из знаменателя закона Кулона (4.9), но появляется в правых частях уравнений (4.1) и (4.3). [Улучшение системы единиц всегда похоже на Тришкин кафтан.]

Кроме того, вместо квадрата скорости света вводят новую постоян­ную m 0=e 0/c 2 , называют ее (довольно неудачно) магнитной проницаемос­тью пустоты (так же, как e 0 называют диэлектрической проницаемостью пустоты) и обозначают e 0E=D, B=m 0H.

Будьте осторожны! Проверяйте систему единиц, когда открываете новую книгу об электричестве!

*Конечно, последующие выкладки в равной мере относятся и к лю­бому прямоугольному параллелепипеду.

Читайте также

Глава 3

Глава 3 Великое открытиеС самого момента открытия Эрстедом влияния электрического тока на магнитную стрелку исследователей стала преследовать мысль: «А нельзя ли решить и обратную задачу: превратить магнетизм в электричество?» Во Франции над этой задачей ломали голову

Глава 4

Глава 4 «Русский свет»«Применение электрической энергии в России за последние годы значительно развилось, электротехническая же промышленность в ней до последнего времени находится в младенческом возрасте». Это строчки из толстой книги профессора Артура Вильке

Глава 1

Глава 1 На подступах к ГОЭЛРОПредприятия Сименса и Гальске, о которых шла речь в книге почтенного профессора Артура Вильке, были разбросаны по разным городам. Но самый большой Электротехнический завод в России (до 150 служащих) находился на Васильевском острове в

Глава 2

Глава 2 Время свершенийСегодня много говорят о получении энергии с помощью Солнца, ветра, морских волн, об извлечении энергии из недр, за счет использования внутреннего тепла Земли, о приручении морских приливов и о выведении электростанций за пределы атмосферы. Но пока…

Глава 14

Глава 14 Незаметно махнув рукой Тому, Тристам занял свое обычное место в последнем ряду. Миртиль бросила беглый взгляд на его руку: вчерашний ожог зажил. Джерри, сидевший рядом с Томом, был вне себя от ярости. Опять этот Тристам дешево отделался! Безобразие! Давно пора

Глава 16

Глава 16 Ветер дул все сильнее. Стебли рисовых метелок нещадно хлестали Тома и Тристама, убегавших от преследователей. Обезумев от страха, мальчики думали только о том, чтобы нагнать г-жу Дрейк. До защитного ограждения было уже недалеко. Возле городской черты мать Тристама

Глава 17

Глава 17 Получасом раньше, в тот самый момент, когда в класс Лазурро вбежал полковник, Миртиль поняла, что для их городка наступили последние часы.— Они нас нашли, — твердо сказал полковник. — Они уже здесь. Миртиль, Тристам, идемте со мной, вы должны бежать.Миртиль

Глава 6

Глава 6 Тюрьма, со слепыми, без единого окна, стенами, размещалась глубоко в недрах облака, на котором была построена Белая Столица. Оказавшись в камере, напуганные Тристам и Том какое-то время молча сидели на кровати, отведенной им на двоих, — в действительности это были

Глава 7

Глава 7 Прошло несколько часов. Тристам и Том лежали на жестких нарах в темной камере без окон, непрестанно ворочаясь с боку на бок. Лишь только напев флейты смолк, старик сразу задремал, что-то неразборчиво бормоча во сне.Тома снова начало знобить; Тристама же разбирал

Глава 8

Глава 8 С прохладным и сыроватым рассветным воздухом смешивался густой дым, валивший из печных труб. На всех перекрестках в центре Белой Столицы были расставлены люди снегобоя. Они походили не столько на стражей порядка, сколько на оккупационные войска.Тристам и Том в

Глава 9

Глава 9 Наступила ночь, за окнами стояла глубокая тишина. Тристам уснул. Рядом с ним, с раскрытой книгой на животе, спал, погруженный в грезы о будущем, Том.В глубине комнаты, растянувшись на матрасе, храпел один из полицейских. Второй сидел на лесенке, стоявшей теперь возле

Глава 10

Глава 10 Тристам внимательно следил за тенью. Она двигалась прямо на военный патруль.«Там ему не проскочить!» — забеспокоился Тристам.Но человек с рюкзаком, наверное, и сам это знал: он вскарабкался по стене и, словно черная кошка, перепрыгивая с крыши на крышу, за считанные

Глава 11

Глава 11 Наутро, как только мальчики проснулись, полицейские повели их вниз, в подземный ход. К счастью, в тесном тоннеле, по которому пришлось продвигаться гуськом, было чисто и сухо.— Долго еще? — спросил Тристам, когда они прошли метров десять.— Тс-с! — шепнул

Источник