Интегрирование это что такое в жизни
Что такое интеграция и что именно можно интегрировать
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Существует множество терминов, которые мы вставляем к месту и не к месту в свою речь, точно не зная, что они обозначают.
К таковым относится и понятие «интеграция». Разберемся, что определяет этот термин, и в каких сферах применяется.
Понятие «интеграция»
В переводе с латыни «интеграция» это «вставка, соединение». Рассуждая логически, делаем вывод, что «интегрировать», значит, вставлять какую-то часть в единое целое.
А «интегрировать» — это значит объединить, слить (например, компании), переплести, вставить, добавить, соединить и т.п.
Простой пример: собирая пазл, мы интегрируем его фрагменты в единую картинку. Развитие человеческого общества – это тоже череда интеграций и дифференциаций (разделения целого на составные части).
Интегрировать что-то можно двумя путями:
По каким принципам можно интегрировать
Интеграция может происходить, основываясь на нескольких принципах. Рассмотрим основные из них подробней.
Пример международной экономической интеграции горизонтальной модели – Евросоюз: страны имеют единую валюту, решают общие политические и экономические проблемы.
Главная цель объединения на основе диагональной модели – это диверсификация, т. е. распределение инвестирования по нескольким направлениям с целью увеличить прибыль и (или) не допустить краха. Иными словами – «раскладывание яиц по разным корзинам».
Наглядный пример – консорциум (объединение независимых предприятий) «Альфа-Групп». Интегрированные в консорциум предприятия занимаются инвестированием, страхованием (что это такое?), розничной торговлей, водоснабжением, производством и реализацией минеральной воды.
Интеграция в различных сферах
Интеграция – это процесс, который актуален для всех сфер жизни человека.
И примеров тому множество:
Интеграция в экономике
Экономическая интеграция (ЭИ) – сближение (или объединение) предприятий, отраслей и регионов. Если ЭИ выходит за рамки одной страны, то тогда речь идет о международной экономической интеграции (МЭИ).
Это создание взаимовыгодных экономических отношений между государствами. Регулируется соглашениями на международном уровне. Подобное сотрудничество дает участникам ЭИ расширенный доступ к материальным, трудовым и финансовым ресурсам, к новейшим технологиям и рынкам сбыта.
Формы МЭИ представлены на схеме:
Что и как можно интегрировать в политике
Политическая интеграция (ПИ) – сближение деятельности политических единиц (государств, политических партий), целью которого является взаимное сотрудничество для достижения определенных результатов, близких всем членам интеграционного сообщества. ПИ бывает 2 видов:
Интеграция в науке и педагогике
Познание человеком сути вещей и явлений – бесконечный процесс. Чем глубже и точнее научные изыскания, тем очевидней, что полноценное изучение какого-либо объекта не может быть проведено в рамках только одной научной дисциплины.
Биохимия – один из примеров симбиоза двух наук – биологии и химии. Невозможно понять принципы жизнедеятельности биологических организмов без знания химических процессов, происходящих в их клетках и тканях.
Приведем еще примеры: геофизика, биофизика, кибернетика и т. д. Следовательно, интеграция наук – это объединение знаний, накопленных в рамках нескольких научных дисциплин, в единое целое для возможности всестороннего изучения объектов, явлений, процессов.
Стремление понять мир, в котором мы живем, диктует необходимость научной интеграции. И это касается не только точных наук. Например, обществознание – это комплекс дисциплин, изучающих все стороны деятельности человеческого общества:
Интеграция в обществознании – это рассмотрение изучаемого объекта не в рамках какой-либо из перечисленных наук, а в их совокупности.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (2)
Интеграция означает жизнь по чужим правилам, если человек интегрируется в общество, значит он берет на себя обязательство подчиняться общественным законам.
Тоже и в межгосударственных отношениях, когда Россия входит в какие-то международные организации, союзы, то так же берет обязательства, что, на мой взгляд, сильно подрывает суверенитет. Мы начинаем зависеть от внешних навязанных нам правил, вряд ли указания некоего дяди могут благоприятно сказываться на благосостоянии народа.
Игорь: хорошо подмечено. Именно от таких ошибочных интеграций лихих девяностых мы сейчас потихоньку и избавляемся. В том числе, и с помощью летних поправок в конституцию
Значение слова «интегрировать»
1. Мат. Найти (находить) интеграл данной функции.
2. Книжн. Объединить (объединять) части, стороны чего-л. в одно целое. Гениальные литературные произведения интегрировали всю сложность слагаемых эпохи. А. Н. Толстой, Больше творческого дерзания.
[От лат. integrare — восстанавливать]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ИНТЕГРИ’РОВАТЬ, и́рую, и́руешь, сов. и несов., что (мат.). Найти (находить) интеграл данной функции.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
интегри́ровать I
1. матем. вычислять интеграл какой-либо функции ◆ Если, например, мы хотим интегрировать относительно переменных у, z, то должны обратить внимание на то, что в элементах dx dz, dx dy нужно взять дифференциал переменной х, рассматривая в первом случае одну только величину у как переменную, во втором — одну только величину z как переменную и т. д. М. В. Остроградский, «Мемуар об исчислении вариаций кратных интегралов», 1834 г. (цитата из НКРЯ) ◆ Вместе с том здесь необходимо столь же отчетливое знание и умение численно интегрировать дифференциальные уравнения, между тем как для учения о пловучести и остойчивости требуется уменье приближенно производить квадратуры. А. Н. Крылов, «Значение математики для кораблестроителя», 1935 г. (цитата из НКРЯ)
интегри́ровать II
1. офиц. включать, встраивать, увязывать; делать составной частью чего-либо ◆ Власть оказалась способной интегрировать в общество новые культурные ценности и социальные цели, т.е. создать механизм адаптации новых целей. Н. Л. Захаров, «Система регуляторов социального действия российских государственных служащих (теоретико-социологический анализ)», 2002 г. (цитата из НКРЯ)
2. офиц. включить, встроить, увязать; сделать составной частью чего-либо ◆ К концу текущего года Агентство планирует интегрировать в систему большинство субъектов РФ. «Новости ипотеки», 29 сентября 2003 г. // «Строительство» (цитата из НКРЯ)
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: горловой — это что-то нейтральное, положительное или отрицательное?
Что такое интеграл и зачем мне знать это
Игорь Гладкобородов
IMAGE 1287 NOT FOUND
Представьте, что у нас есть какая-то функция зависимости чего-то от чего-то.
Например, вот так примерно можно на графике представить скорость моей работы в зависимости от времени суток:
Скорость я измеряю в строках кода в минуту, в реальной жизни я программист.
Объем работы — это скорость работы умножить на время. То есть если я пишу 3 строки в минуту, то в час получается 180. Если у нас есть такой график, можно узнать, сколько работы я сделал за день: это площадь под графиком. Но как это посчитать?
Разделим график на столбики равной ширины величиной в час. А высоту этих столбиков сделаем равной скорости работы в середине этого часа.
Площадь каждого столбика по отдельности легко посчитать, надо умножить его ширину на высоту. Получается, что площадь каждого столбика — это сколько примерно я работы сделал за каждый час. А если просуммировать все столбики, то получится примерная моя работа за день.
Проблема в том, что результат получится примерный, а нам нужно точное число. Разобьем график на столбики по полчаса:
На картинке видно, что это уже гораздо ближе к тому, что мы ищем.
Так уменьшать отрезки на графике можно до бесконечности, и каждый раз мы все ближе и ближе будем подходить к площади под графиком. А когда ширина столбиков будет стремиться к нулю, тогда сумма их площадей будет стремиться к площади под графиком. Это и называется интегралом и обозначается вот так:
В этой формуле f(x) означает функцию, которая зависит от величины x, а буквы a и b — это отрезок на котором мы хотим найти интеграл.
Зачем это нужно?
Ученые стараются все физические явления выразить в виде математической формулы. Как только у нас есть формула, дальше уже можно при помощи нее посчитать что угодно. А интеграл — это один из основных инструментов работы с функциями.
Например, если у нас есть формула круга, мы можем при помощи интеграла посчитать его площадь. Если у нас есть формула шара, то мы можем посчитать его объем. При помощи интегрирования находят энергию, работу, давление, массу, электрический заряд и многие другие величины.
Нет, зачем мне это нужно?
Да низачем — просто так, из любопытства. На самом деле интегралы входят даже в школьную программу, но не так много людей вокруг помнят, что это такое.
Интеграл простыми словами
Интегралы начинают изучать еще в школе. Но никто из учителей не говорит, зачем это нужно, как использовать эти знания в жизни. Мало кто вообще способен объяснить простыми словами, что такое интеграл, даже в университете. А мы попробуем.
Простыми словами…
Если коротко — интеграл, это сумма маленьких частей. Да, точно так же как и сложение 2+2, только части бесконечно маленькие, естественно и количество их — бесконечно.
Знак интеграла ∫ — это вытянутая буква s (длинная «эс» существовала до начала 19-ого века писалась так — ſ). Первая буква слова summa.
Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.
Почему обычного «плюсования» не достаточно? Просто в алгебре нет никаких бесконечно малых или больших.
Бесконечно малая величина, это не какое-то конкретное число. Это абстракция, в реальном мире аналогов просто нет. Мы придумали так для удобства. Что-то настолько маленькое, что измерять его бессмысленно, но в расчетах использовать можно.
Слово «интеграл» происходит от латинского integer, что означает «целый». Даже в названии есть намек некое действие, что-то вроде восстановления чего-то целого.
Лучше всего показать «на пальцах», точнее на примере. Предположим, мы хотим узнать площадь фигуры как на картинке (она называется криволинейная трапеция, потому, что одна из сторон создана кривой линией). Зачем нам это нужно? Например, это часть крыла самолета и нужно знать его площадь.
Можно, конечно, разбить фигуру на две, прямоугольник и треугольник.
Но останется «пробел», площадь которого будет неизвестна. Чтобы увеличить точность, можно разделять на большее количество фигур, но все равно будет оставаться какая-то, пусть и небольшая, но «не закрашенная» область. Фигуры будут становиться все меньше и меньше… Очевидно, что процесс измельчения будет бесконечным, по крайней мере в воображении.
Но, в реальности, бесконечный процесс попросту не нужен. На самом деле вычислить такие вещи как площадь круга, длину диагонали квадрата или объем пирамиды невозможно, значение будет бесконечным, естественно, практического смысла бесконечные числа не имеют и мы их «округляем» до нужного предела точности — приблизительно.
Такой метод в Древней Греции назывался «исчерпание». Аналогия с водой тут очень уместна, если представить, что черпаешь из ведра при помощи кружки, то сначала кружки будут полные, но чем ближе ко дну, тем меньший объем будет попадать в кружку. Первой известной личностью «взявшей интеграл» был Архимед, он фактически решил задачу по нахождению площади круга и площади параболы ничего не зная ни про пределы, но даже про число «пи».
Чем больше будет фигур, тем больше будет и точность расчета и тем меньше будут сами фигурки. Если площадь маленьких фигурок будет бесконечно малой, то есть стремится к нулю (но не равняться ему), сумма всех этих площадей будет равна сумме большой фигуры с бесконечно большой точностью.
То же самое происходит при интегрировании:
Фигура на картинке разбивается на столбцы бесконечно маленькой ширины. Ширина у нас Х. Бесконечно малое число обозначается d. То есть dx — это бесконечно малый «икс».
Сложение бесконечного числа частей бесконечно маленького размера это и есть интегрирование.
Чтобы узнать площадь фигуры нужна еще высота, а это y. Высота везде не одинаковая, она постоянно меняется. И мы знаем как именно! Ведь кривая может быть (а может и не быть, но в нашем случае так и есть) функцией y=f(x), то есть значение у меняется по закону (буква f об этом говорит) зависимому от х. Поэтому «эф от икс». Значит высота это f(x). Функция, кстати, тоже бесконечная.
Высота конкретного прямоугольничка, это значение функции в этой конкретной точке (почему точке, потому, что ширина полоски у нас бесконечно маленькая, мы так договорились в самом начале).
Площадь, это высота умноженная на ширину. За высоту можем брать и y и f(x), они равны. За ширину у нас играет dx. Итак, момент истины:
f(x)dx — площадь нашего маленького столбика. В если собрать из все вместе, будет сумма бесконечно маленьких столбиков.
А площадь нужна не бесконечной фигуры, а той что начинается от 1 и закачивается на 5. Если написать эти цифры над и под значком интеграла, получится определенный интеграл.
Собственно и все, интеграл — это сумма бесконечно малых приращений (то есть значений) какой-то функции. Не сложно и не страшно, если не усложнять.
Что мы делаем? Разрезаем фигуру на «ленточки» изменяем площадь этих ленточек и собираем все обратно (суммируем).
Интересно, везде идет речь о сумме, а площадь считается умножением. Парадокс? Нет, умножение это ведь то же самое, что и сложение: 2+2+2+2=2*4. То же самое происходит и с площадью. Чтобы выяснить какова площадь прямоугольника со сторонами 5 и 4, перемножаем 5 на 4, или разделяем прямоугольник на 5 полосок шириной в «единицу» и складываем 4+4+4+4+4=5*4=20.
Никакого противоречия здесь нет. Вот только умножение работает в случае одинаковых величин, простых фигур или прямолинейного движения без ускорения. В остальных случаях — интегрирование.
Зачем нужен интеграл
Из примера выше уже понято, что одна из полезных задач интегрирования — это расчет площади криволинейных фигур. В любой сложной ситуации, если сложность эта заключается криволинейности или неравномерности мы используем интеграл.
Но лучший способ объяснить, что такое интеграл простыми словами — показать еще пару примеров. Как когда-то в детстве объяснили сложение на яблоках. Для чего интеграл может понадобиться?
Предположим, нужно построить храм кому-то из древнегреческих богов, такой чтобы место в нем хватило всем, крыша была прямоугольной, а колоны круглыми, ведь так красивее (а еще прочнее).
Давление колонны на фундамент легко посчитать, если она квадратного сечения, делим силу на площадь и вуаля. А если колонна круглого сечения? Какова площадь круга?
Можно конечно, не напрягаться, и заменить круг эквивалентным квадратом (квадратура круга), но каким? На всякий случай побольше, чтобы наверняка ничего не развалилось. Но это не наш метод, особенно, если ни бесконечного числа рабочих, ни бесконечного числа мрамора в действительности нет и взять негде, а казнить за неэффективное использование бюджета никто не запрещает.
Прием с эквивалентом площади на самом деле простой, использовался древними людьми. Очень-очень древние греки ничего не знали об интегрировании, а Архимед еще не родился, тем не менее, чтобы рассчитать площадь круга, в него выкладывались камешки. Когда круг заполнялся, камешки собирались и раскладывались в виде квадрата. Чем меньше камешки тем… Ничего не напоминает?
Еще примеры из жизни
Конечно, в физике интеграл «берут» постоянно. Вместо Х, может быть время, и тогда мы будем иметь дело с функцией времени, такой, например, как скорость. Ускорение — это скорость изменения скорости. Скорость, это скорость изменения координат. Пробежавшись от ускорения к скорости мы уже дважды использовали интеграл.
В обратную сторону: первая производная пути, это скорость, вторая производная — ускорение. Если ускорение равно нулю, значит скорость не менялась.
Интегрирование и дифференцирование, такие же «парочка» как и умножение и деление, суммирование и вычитание, только не с цифрами, а с функциями. Это взаимно-обратные операции. В случае производной, мы не «складываем», а «отнимаем».
Если проинтегрировав функцию изменения скорости (ускорение) получим константу (число, например, 60, а не формулу y=2x), значит, скорость не изменялась со временем, ускорения не было. Если, взяв приводную (дифференциал) функции скорости по времени, получим ноль — скорость не менялась, ускорение равно нулю.
То есть, имея в своем распоряжении какую-то функцию (зависимость чего-то от чего-то), мы можем ее дифференцировать или интегрировать. Точно также как если бы умножали и или, вычитали и складывали обычные числа.
Например, у нас есть функция изменения координат от времени. В реальном мире мы вышли на пробежку. Бежал наш виртуальный спортсмен 30 минут, первые 10 минут очень быстро, вторые 10 минут уже с одышкой, ну а последние 10 прошел пешком.
Очевидно, что координаты бегуна в начале и в конце разные (он же не стоял на месте). Если координаты менялись — скорость не равнялась нулю.
Скорость не была одинаковой, а менялась в зависимости от времени (больше времени, больше усталость, меньше скорость).
Итак, у нас есть функция изменения координат. Первая производная даст нам новую функцию — изменения координат, вторая производная — функцию ускорения. И первая и вторая функции зависят от одной и той же переменной — времени.
Еще один пример, вычисление массы. Масса, это произведение плотности на объем. Если плотность и объем одинаковы (это стакан воды) никаких проблем нет. А если плотность меняется (тот же стакан, только с коктейлем в несколько слоев)? В таком случае нужно знать закон (зависимость с которой изменяться плотность жидкости в стакане).
Если вам такие примеры не близки, то представьте себе, что взяли кредит под сложный процент. Тогда ваш долг будет расти не линейно. И вы будете интегрировать…
Если нужно узнать какую работу нужно затратить на перемещение предмета не по прямой, а если, нужно рассчитать лучшую цену, зная зависимость спроса от предложения, а если нужно посчитать за какое время рабочие выкопают яму, если это не роботы, а живые люди, которые устают со временем, а если…
Если посмотреть вокруг, не найдется в реальном мире ни идеальных фигур, ни ровных графиков, ни равномерного движения без ускорения, ни линейных зависимостей в поведении человека «разумного».
Все эти простые штуки из науки, просто частные случаи. А значит, в реальном мире интеграл более полезен, чем кажется. Конечно, кривые сложнее прямых и именно поэтому всю свою историю люди упрощали себе жизнь: делили поле прямыми, на квадраты и прямоугольники при помощи натянутой веревки. Считали среднюю скорость, а не мгновенную в каждой точке маршрута, полагали, что тело прошенное под углом к горизонту летит по параболе, а не баллистической кривой… Но, просто — не значит точно.
Говоря простым языком, интегрирование — это такой же инструмент, как и суммирование, в нем нет никаких особых тайн и сложностей. Кроме одной — представить себе бесконечность сложнее, чем натуральные числа, у которых есть наглядные представления в природе. Но справляемся же мы как-то с представлениями таких абстракций как «ноль» или «отрицательное число». С матанализом просто нужно чуть больше воображения.
Ну а если уж совсем просто, для гуманитариев, то производная винограда — это вино. Интеграл вина — это виноград.
Сегодня вы поймёте, что такое интеграл в математике
(и в программировании)
Недавно мы разобрали, что такое знаки Σ и П в математике — это операции, которые, по сути, похожи на циклы в программировании. В одном случае мы складывали много чисел по определённому принципу, а в другом — умножали.
Сегодня посмотрим на интеграл ∫ — что это такое и какой цикл можно сделать из него.
Но сначала: что такое функция
Интегралы в математике всегда связаны с функциями, поэтому сначала поговорим про них.
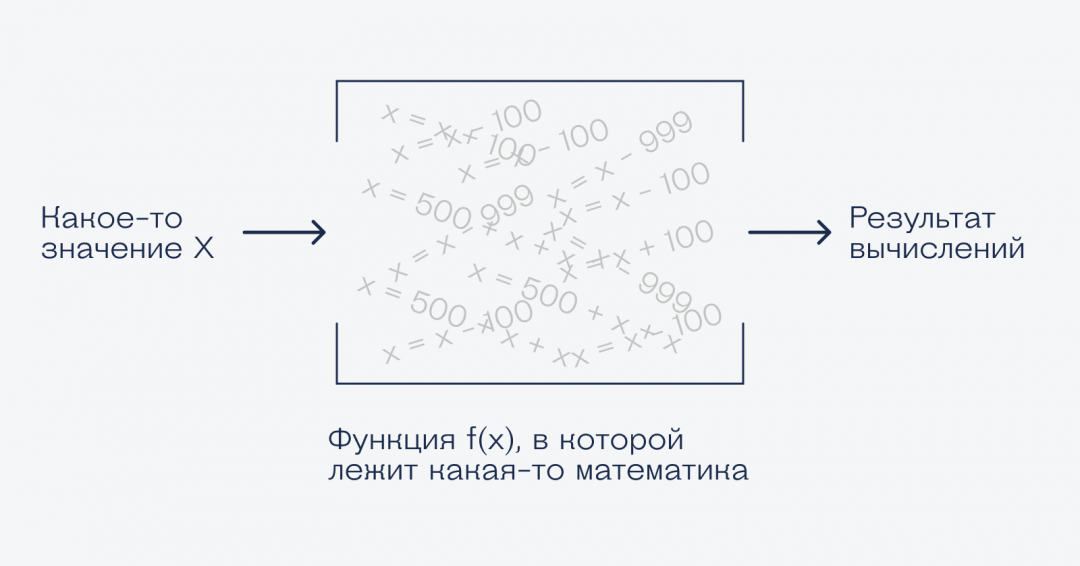
Функцию можно представить как «коробку с математикой». У тебя есть какая-то масса математических операций, ты их «запаковываешь» в функцию. Теперь ты можешь эту массу операций вызывать в своих математических выражениях одним действием.
У функции есть один или несколько аргументов — это те числа, к которым нужно применить массу математических операций. Можно представим, что мы засунули это число в коробку с математикой, потрясли и получили на выходе другое число.
Если посчитать f(x) для одного числа, получится другое число. Если посчитать f(x) от 100 чисел, получится 100 других чисел. А если непрерывно считать f(x) для бесконечного количества чисел, то получится бесконечное количество других чисел.
Что такое интеграл
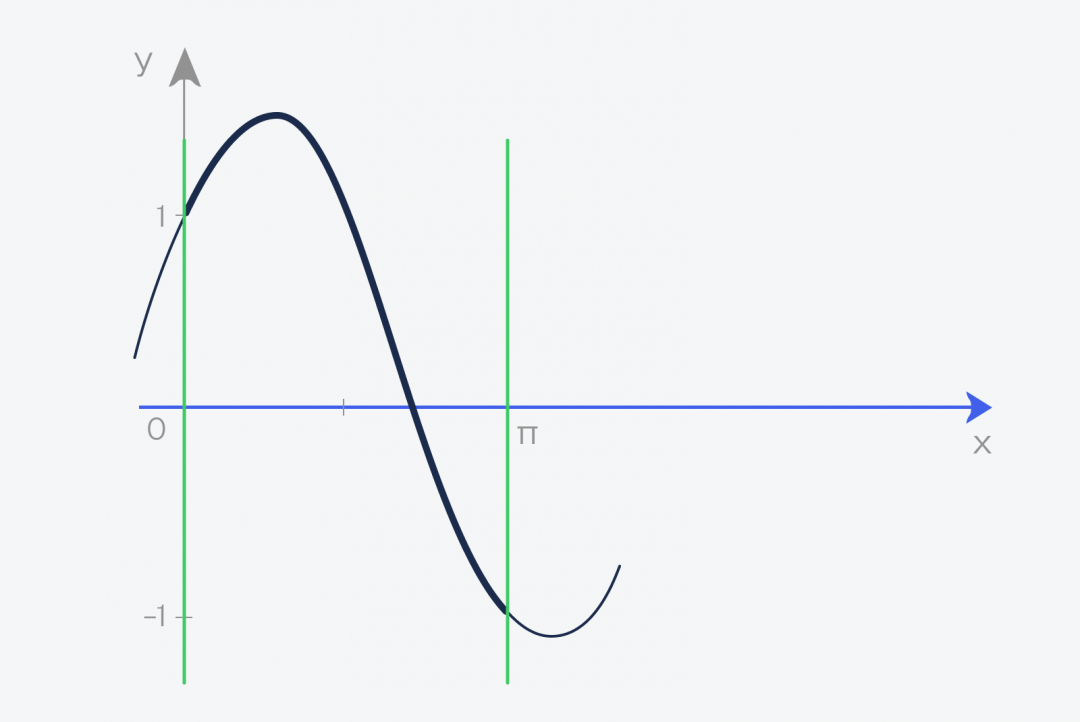
Итак, у нас есть некая функция, у неё есть числа на входе и числа на выходе. Эти пары чисел можно использовать для построения графика функции.
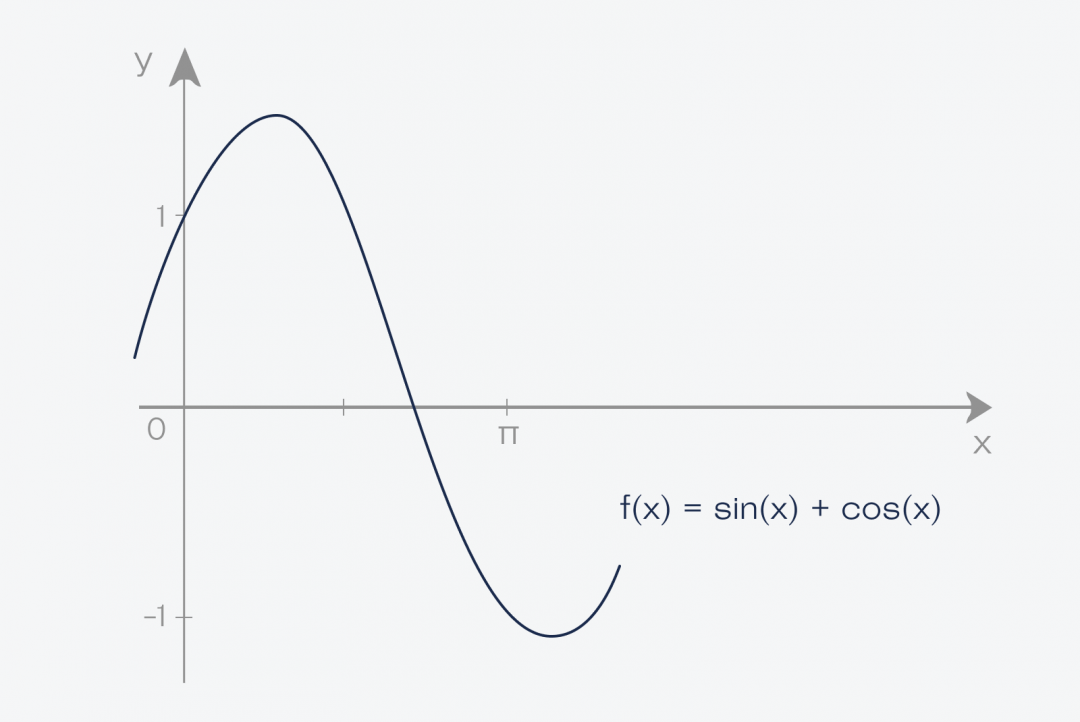
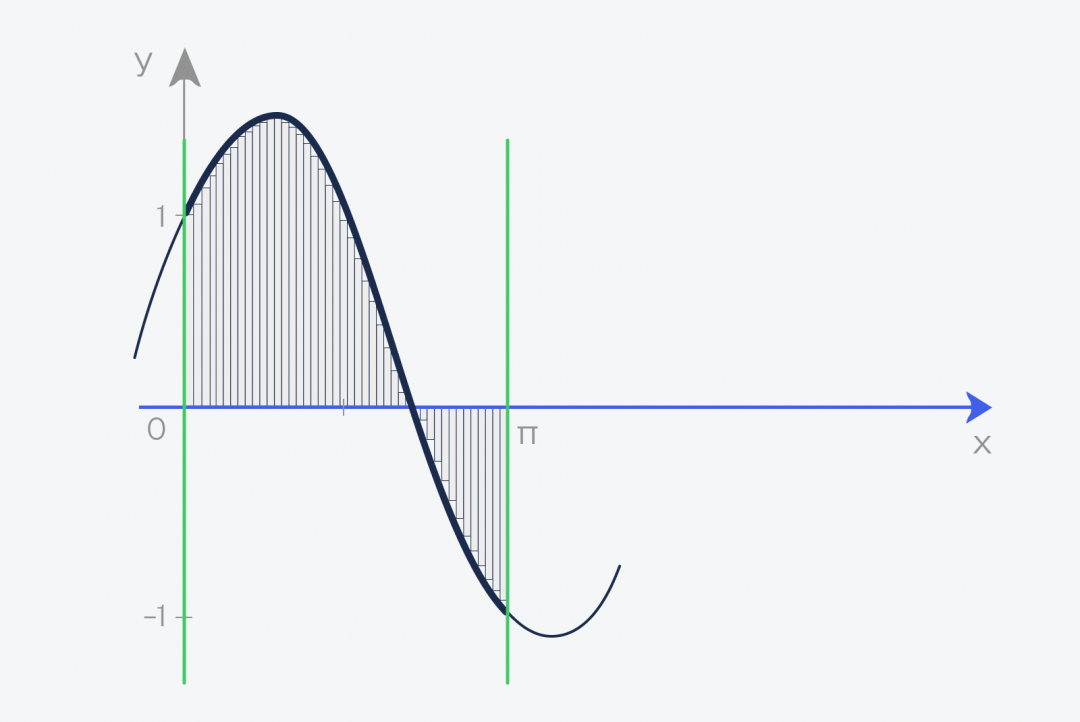
Теперь берём этот график функции и проводим две линии, которые ограничивают график. Получается фигура, которая сверху зависит от нашей функции, а с остальных сторон ограничена прямыми линиями и осью:
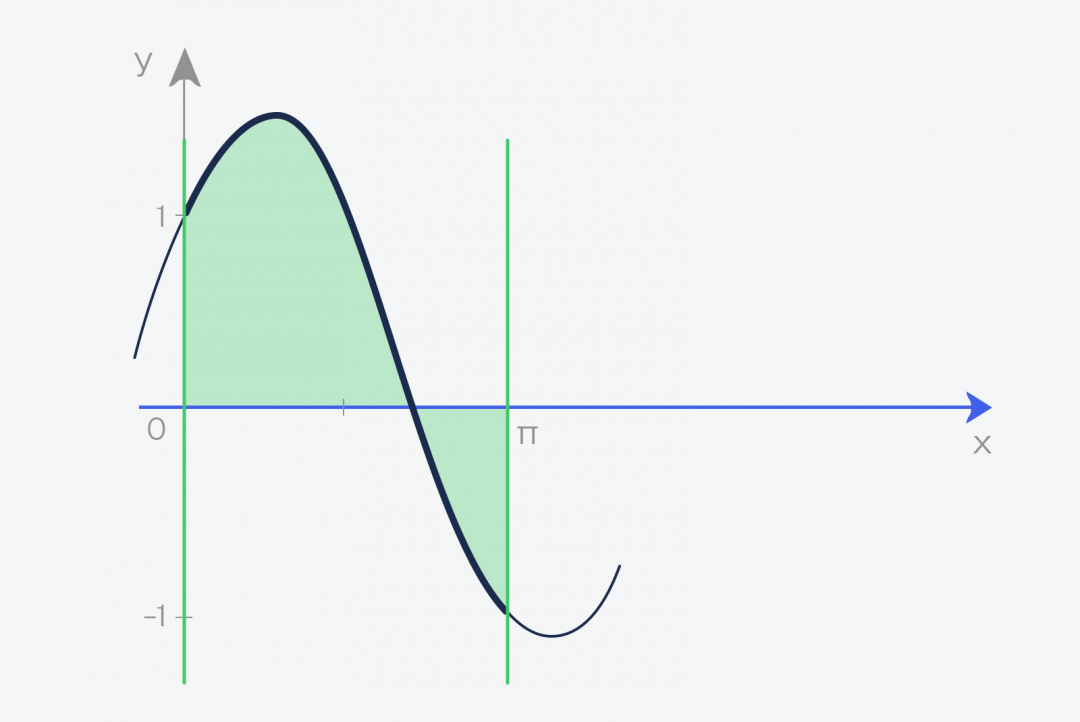
А теперь то, ради чего всё это затевалось:
✅ Площадь этой фигуры и есть интеграл функции f(x) = sin(x) + cos(x) на отрезке от a до b
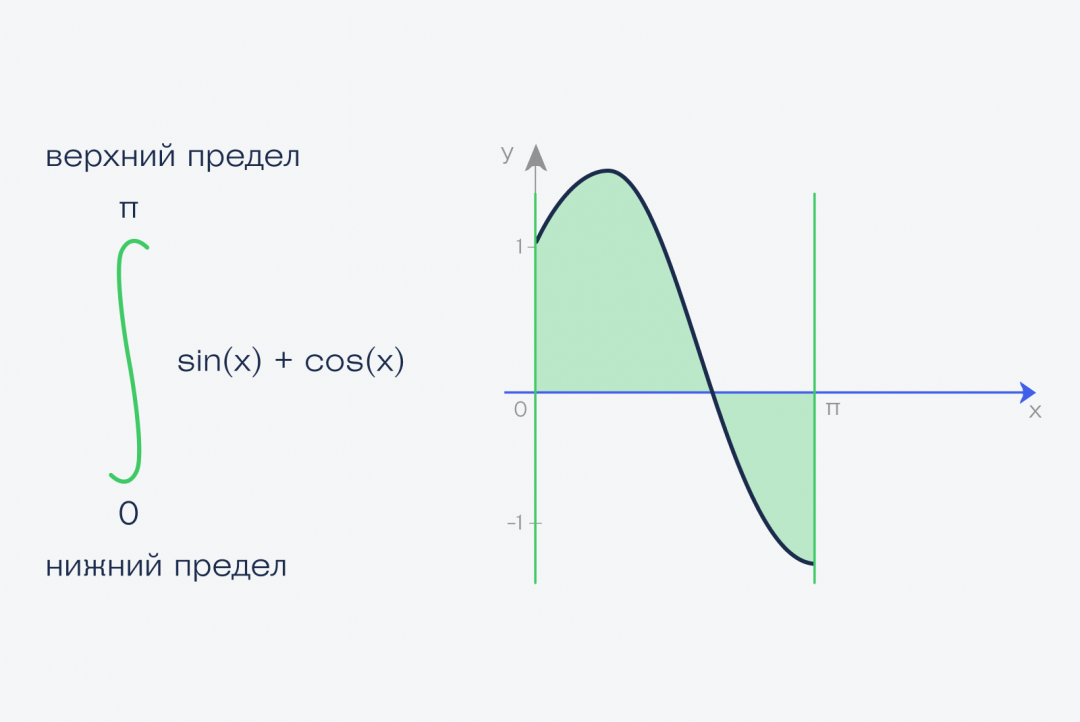
В нашем случае мы считаем интеграл от нуля до числа пи — 3,1415926.
Это называется определённый интеграл. Определённый — это когда у нас определены начало и конец фигуры — в математике это называют пределами интегрирования. Записывается этот интеграл так:
В математике есть ещё неопределённые интегралы, у которых нет пределов интегрирования. Ими мы заниматься не будем, потому что ответом к неопределённому интегралу будет не конкретное число, а формула.
Зачем нужны интегралы в народном хозяйстве
Вы удивитесь, но в первую очередь интегралы нужны, чтобы находить площади и объёмы. В буквальном смысле: вот фигура, вот её описание в виде функции, проинтегрировали — узнали площадь. Будете, например, заливать бетоном красивую кривую дорожку — узнаете, сколько вам нужно бетона.
Интегралы нужны в математике и физике, это один из инструментов вычислений.
Если вы астрофизик, интеграл поможет вам рассчитать какие-нибудь свойства звёзд с течением времени. А математики говорят, что в интегралах не нужно искать практический смысл; их нужно любить, как мать, и почитать, как отца.
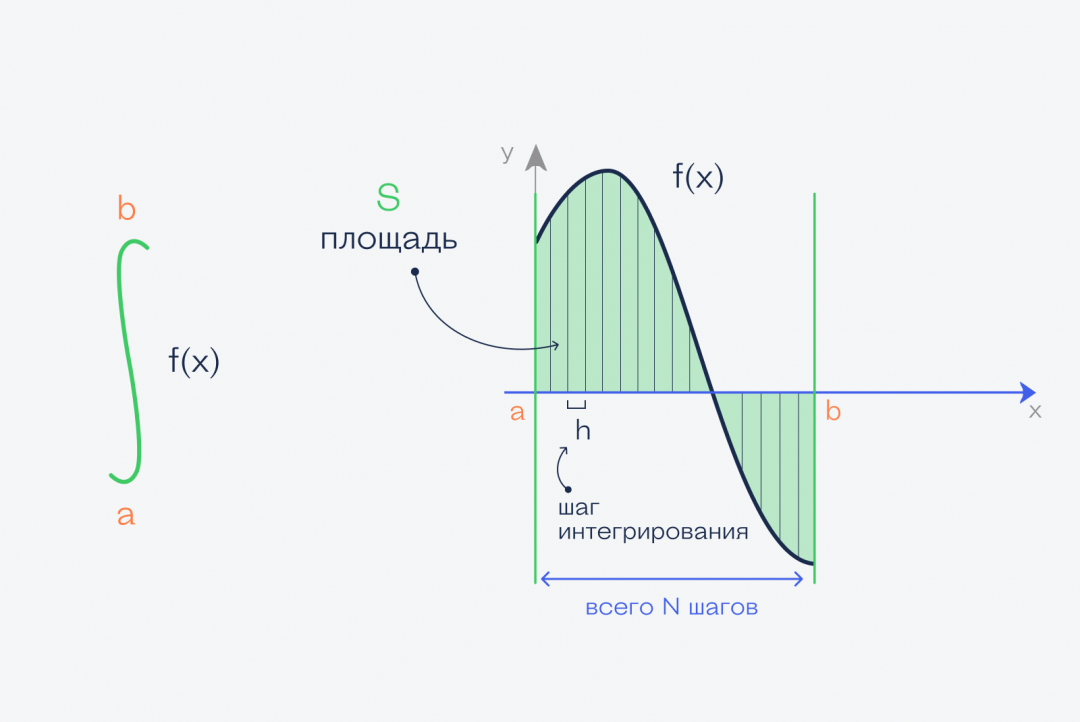
Как посчитать интеграл (то есть найти площадь)
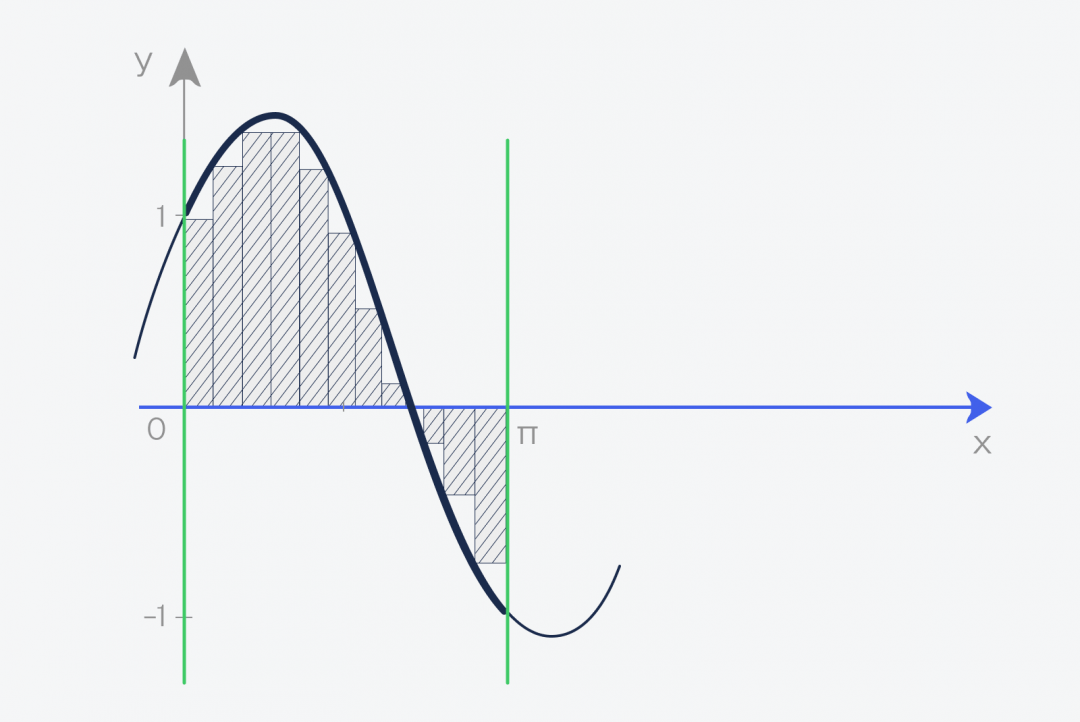
Если бы у нас был прямоугольник, то всё просто: перемножаем высоту на ширину. Если бы была трапеция, тоже ещё как-то что-то можно. Но сверху у нас кривая, поэтому так сделать не получится. Решение придумали такое:
Минус такого подхода в том, что, как бы мы ни старались, прямоугольники не могут повторить все изгибы, и появится погрешность. С другой стороны, чем тоньше будут эти прямоугольники, тем точнее будет ответ. Получается, что наша задача — нарезать фигуру как можно тоньше.
Теперь задача становится намного проще: мы просто считаем площадь каждого прямоугольника и складываем их вместе. В таком виде задачу уже можно решить простым алгоритмом.
Пишем код
Раз нам нужно разбить интервал на много частей а потом с каждой из них сделать одно и то же, то это точно задача для цикла. Для этого нам понадобится шаг цикла — какой ширины будут наши прямоугольники, чтобы бы могли их одинаково перебирать.
Чтобы посчитать шаг, находим расстояние между конечной и начальной точкой и делим на желаемое количество прямоугольников (это будет нашей точностью интегрирования).
Общая логика работы будет такая:
На картинке — все исходные данные, а ниже — код, который считает интеграл. Смотрите на картинку и читайте комментарии: так будет ещё проще разобраться в коде:
Что дальше
Теперь этот код можно изменить так, чтобы он считал интеграл в любых пределах у любой функции. С точки зрения математики это не самый точный результат, но всё зависит от того, сколько точных знаков после запятой нам нужно.
В следующей серии продолжим разбираться со страшной математикой. Если есть пожелания для разбора — напишите в комментариях.