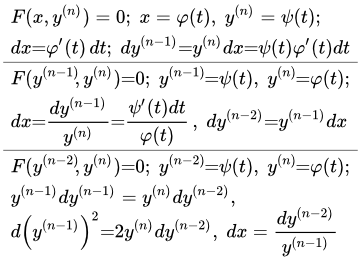Интегрируется в квадратурах что это

Интегрируется в квадратурах что это

Далее мы рассмотрим три типа уравнений высшего порядка, которые интегрируются в квадратурах.

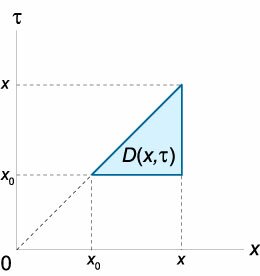
Повторный интеграл в выражении для \(y\left( x \right)\) можно преобразовать к однократному интегралу. Действительно, в случае \(n = 2\) рассмотрим интеграл \[y\left( x \right) = \int\limits_<>^x \int\limits_<>^x ,\] в котором через \(\tau\) обозначена переменная интегрирования во внутреннем интеграле.

Данный повторный интеграл задан в треугольной области \(D\left( \right),\) изображенной на рисунке \(1.\)

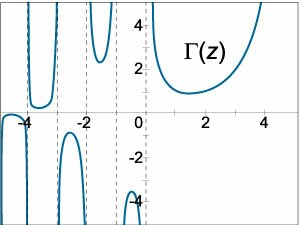
Данную формулу можно рассматривать как определение дробной производной порядка \(z,\) если исходная функция \(y\left( x \right)\) известна или как определение интеграла дробного порядка \(z,\) если задана соответствующая производная.

Это уравнение типа \(3.\) Вводим новую функцию \(z = y’,\) так что уравнение будет записываться в виде \[z»z = 1,\;\; \Rightarrow z» = \frac<1>.\] Очевидно, что \(z = y’ \ne 0\) и \(z’ = y» \ne 0.\) Умножим обе части полученного уравнения на \(2z’\) и проинтегрируем один раз: \[ <2z'z'' = \frac<<2z'>>,>\;\; <\Rightarrow d<\left( \right)^2> = \frac<<2dz>>,>\;\; <\Rightarrow <\left( \right)^2> = 2\ln \left| z \right| + \ln = \ln \left( <> \right).> \] Видно, что уравнение приведено к типу \(1.\) Далее его удобно решать параметрическим методом. Положим \(z’ = t,\) где переменная \(t\) рассматривается как параметр. Функция \(z\) выражается через \(t\) следующим образом: \[ <= \ln \left( <> \right),>\;\; <\Rightarrow = >>,>\;\; <\Rightarrow z = \pm \frac<1><<>>>>.> \] Таким образом, функция \(z\) представлена в виде \(z = \varphi \left(> \right).\) Зависимость переменной \(x\) от параметра \(t\) также описывается квадратурой: \[><>,>\;\; <\Rightarrow dx = \frac<>= \frac<<\varphi '\left(> \right)dt>>,>\;\; <\Rightarrow x = \int <\frac<<\varphi '\left(> \right)dt>>> + .> \] Остается получить параметрическое выражение для функции \(y.\) Поскольку \[ ><>,>\;\; <\Rightarrow dy = zdx = \frac<<\varphi \left(> \right)\varphi ‘\left(> \right)dt>>,> \] то после интегрирования имеем: \[y = \int <\frac<<\varphi \left(> \right)\varphi ‘\left(> \right)>>dt> + .\] Итак, общее решение исходного уравнения в параметрической форме выражается через квадратуры в следующем виде: \[ > \right)>>dt> + ,>\;\;\; > \right)\varphi ‘\left(> \right)>>dt> + .> \] где \(\varphi \left(> \right) = \pm <\large\frac<1><<>>\normalsize>>>\) и \(,,\) − постоянные интегрирования.

Источник

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Здесь рассмотрены методы решения дифференциальных уравнений высших порядков, решаемые в квадратурах, то есть решения которых можно выразить через конечное число интегралов. К таким уравнениям относятся следующие типы:
⇓
⇓
⇓
Также приводятся подробно разобранные примеры решений ⇓ таких уравнений.

F(x, y (n) ) = 0: Дифференциальные уравнения, содержащее только независимую переменную и производную n-го порядка

y (n) = f(x) Разрешенные относительно старшей производной

x = f(y (n) ) Разрешенные относительно независимой переменной

F(x, y (n) ) = 0 Общий случай

Общий случай

y (n-1) = f(y (n) ) Разрешенные относительно младшей производной

Рассмотрим частный случай уравнения (2.1.1), в котором производная меньшего порядка выражена через старшую производную:
.

Это уравнение интегрируется в квадратурах, введением параметра
.
Тогда
.
Из этих уравнений
;
;
;
.

y (n) = f(y (n-1) ) Разрешенные относительно старшей производной

Но в любом случае можно получить решение в параметрическом виде.
;
.

Общий случай

Примечание. В литературе иногда не ставят знак плюс-минус. При этом подразумевают, что корень является многозначной функцией и автоматически может быть как положительным, так и отрицательным.

y (n) = f(y (n-2) ) Разрешенные относительно старшей производной

Примеры решений задач

Все примеры Далее рассматриваются примеры с подробными решениями следующих дифференциальных уравнений.
⇓
⇓
⇓
⇓
⇓

Пример 1

Используя (П1.3) и (П1.4), аналогично предыдущему имеем:

;

.

Пример 2

Однако это не означает, что представление (П2.3) автоматически эквивалентно уравнению (П2.1). Поскольку кубическое уравнение может иметь три действительных корня, то, возможно, уравнение (П2.3) можно представить в параметрическом виде тремя неэквивалентными способами. Также возможен случай, когда условия теоремы существования и единственности решения дифференциального уравнения не выполняются, и заданным начальным условиям будут удовлетворять несколько решений. Все это нужно иметь в виду при решении подобных уравнений. Но нам нужно найти любое решение, удовлетворяющее заданным начальным условиям. Поэтому попробуем применить для этой цели представление (П2.3).

Пример 3

Интегрируя, находим выражение зависимой переменной через параметр t :
.

Пример 4

Исключим параметр t из уравнений (П4.4) т (П4.6).
;
.

Примечание.
Эту задачу можно решить проще, если с самого начала выбрать следующее параметрическое представление для производных:
.

Пример 5

Уравнение имеет вид (3.2.3). В нем вторая производная выражена через функцию (зависимую переменную y ). Решаем изложенным выше методом ⇑.

Возводим в квадрат и выполняем преобразования:
;
.
Извлекаем квадратный корень:
.
Выбираем знак плюс или минус из начальных условий (П5.2). Подставляем :
.
Этому уравнению удовлетворяет знак плюс. Тогда
.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Источник

Некоторые виды уравнений, интегрируемых в квадратурах

По этой ссылке вы найдёте полный курс лекций по математике:

общем случае, даже зная, что решение уравнения существует, отыскать его довольно трудно. Однако существуют некоторые виды дифференциальных уравнений, методы получения решений которых особенно просты (при помощи интегралов от элементарных функций). Рассмотрим некоторые из них. 5.1. Уравнения с разделяющимися переменными Уравнение вида называется дифференциальным уравнением с разделенными переменными. Здесь f\(y), /2 (я) — известные непрерывные функции своих аргументов.

Покажем, как найти решение этого уравнения. Пусть F\(y) и F2(x) — первообразные функции f\(y) и /2(2) соответственно. Равенство (1) равносильно тому, что дифференциалы этих функций должны совпадать Отсюда следует, что где С — произвольная постоянная. Разрешая последнее уравнение (2) относительно у, получим функцию (может быть, и не одну) которая обращает уравнение (1) в тождество и значит, является его решением Например, — уравнение с разделенными переменными.

Записав его в виде и интегрируя обе части, найдем общий интеграл данного уравнения: Уравнение вида в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от х и только от уу называется дифференциальным уравнением с разделяющимися переменными, так как путем деления на 4>\(y)fi(x) £ 0 оно приводится к уравнению с разделенными переменными Пример 1.

Например, разделяя переменные в уравнении получаем а после интегрирования — откуда (здесь С может принимать как положительные, так и отрицательные значения, но С Ф 0). При делении на у потеряно решение которое может быть включено в общее решение у = Сх, если постоянной С разрешить принимать значение С = 0. Если считать переменные х и у равноправными, то уравнение теряющее смысл при х = 0, надо дополнить уравнением которое имеет очевидное решение х = 0. где /j (ж, у) = у^у, используя уравнение (4′) там, где уравнение (4) не имеет смысла, а уравнение (4′) имеет смысл.

Некоторые дифференциальные уравнения путем замены переменных могут быть приведены к уравнениям с разделяющимися переменными. Например, уравнение вида где f(z) — непрерывная функция своего аргумента, а, Ь, с — постоянные числа, подстановкой z = ах + by + с преобразуется в дифференциальное уравнение с разделяющимися переменными: откуда После интегрирования получаем Заменяя в последнем соотношении найдем общий интеграл уравнения (5). Пример 2.

Проинтегрировать уравнение В общем случае наряду с дифференциальным уравнением следует рассматривать уравнение 4 Положим z = x + y, тогда откуда Интегрируя, находим или Подставляя вместо z величину х + у, получаем общее решение данного уравнения Пример 3. Известно, что скорость радиоактивного распада пропорциональна количеству х еще не распавшегося вещества. Найти зависимость х от времени t, если в начальный момент t = to имелось х = х0 вещества.

Дифференциальное уравнение процесса dx Здесь к > 0 — постоянная распада — предполагается известной, знак указывает на уменьшение х при возрастании t. Разделяя переменные в уравнении и интегрируя, получаем откуда х = Се

и. Учитывая начальное условие = xq, находим, что С — х0ек1с, поэтому Любой процесс (не только радиоактивный распад), при котором скорость распада пропорциональна количеству еще не прореагировавшего вещества, описывается уравнением (*).

Тогда к > 0 при п и к при тп. Если в момент t = О величина популяции равна уо, то уравнение приводит к экспоненциальному закону изменения популяции Предположение, что величины шип являются постоянными, не выполняется для больших популяций. Действительно, большое число членов популяции приводит к уменьшению соответствующих ресурсов, что снижает скорость рождаемости и увеличивает скорость умирания. Это можно задать простейшими законами положительные постоянные.

Возможно вам будут полезны данные страницы:

Например, для функции так что однородная функция относительно переменных х и у второго измерения. Для функции имеем есть однородная функция нулевого измерения. Дифференциальное уравнение первого порядка называется однородным относительно х и у, если функция f(x, у) есть однородная функция нулевого измерения относительно переменных х и у.

Пусть имеем дифференциальное уравнение однородное относительно переменных хну. Положив t = ^ в тождестве получим т. е. однородная функция нулевого измерения зависит только от отношения аргументов. Обозначая / (I, |) через (*), видим, что однородное относительно переменных ж и у дифференциальное уравнение всегда можно представить в виде При произвольной непрерывной функции переменные не разделяются. Введем новую искомую функцию u(z) формулой и = J, откуда у = хи.

Подставляя выражение ^ = и 4- в уравнение (6), получаем Деля обе части последнего равенства на и интегрируя, находим Заменяя здесь и на его значение \, получаем общий интеграл уравнения (6). Пример 4. Проинтегрировать уравнение Положим уравнение преобразуется к виду Интегрируя, найдем или Пример 5. Найти форму зеркала, собирающего пучок параллельно падающих на него лучей в одну точку.

Прежде всего, зеркало должно иметь форму поверхности вращения, так как только для поверхности вращения все нормали к поверхности проходят через ось вращения. Выберем прямоугольную декартову систему координат так, чтобы лучи были параллельны оси Ох и чтобы точкой, в которой собирались бы отраженные лучи, явилось бы начало координат. Найдем форму сечения зеркала плоскостью хОу. Пусть уравнение сечения есть ) (рис.6).

Первое из них путем замены | = и преобразуется к виду — произвольная постоянная. Решение неоднородного уравнения (10) ищем в виде — новая неизвестная функция. Вычисляя производную и подставляя значения и у в исходное уравнение (10), получаем dx откуда — новая произвольная постоянная интегрирования. Следовательно, Это есть общее решение линейного неоднородного дифференциального уравнения (10).

В формуле (14) общего решения неопределенные интегралы можно заменить определенными интегралами с переменным верхним пределом: Здесь С = у(жо) = уо, поэтому общее решение уравнения (10) можно записать в виде (15) где роль произвольной постоянной играет начальное значение уо искомой функции у (ж). Формула (15) является общим решением уравнения (10) в форме Коши.

Отсюда следует, что если р(х) и q(x) определены и непрерывны в интервале то и решение у(х) уравнения (10) с любыми начальными данными у(ж0) = уо будет непрерывным и даже непрерывно дифференцируемым при всех конечных значениях ж, так что интегральная кривая, проходящая через любую точку (жо, уо), будет гладкой кривой в интервале Поэтому сначала интегрируем соответствующее однородное уравнение общее решение которого имеет вид Пример б.

Рассмотрим дифференциальное уравнение, описывающее изменение силы тока при замыкании цепи постоянного электрического тока. 4 Если R — сопротивление цепи, Е — внешняя ЭДС, то сила тока / = /(f) постепенно возрастает от значения, равного нулю, до конечного стационарного значения ^. Пусть L — коэффициент самоиндукции цепи, роль которой такова, что при всяком изменении си- лы тока в цепи появляется электродвижущая сила, равная L-^ и направленная противоположно внешней ЭДС.

На основании закона Ома, по которому в каждый момент t произведение силы тока на сопротивление равно фактически действующей ЭДС, получаем ) Уравнение (*) есть линейное неоднородное уравнение относительно I(t). Нетрудно видеть, что его частным решением является функция Общее решение соответствующего однородного уравнения откуда общее решение неоднородного уравнения («):

(10), после элементарных преобразований получим Выберем в качестве v(ar) любое частное решение v(«) ^ 0 уравнения Тогда в силу (17) для и(ж) получим уравнение которое без труда интегрируется в квадратурах. Зная v(x) и и(х), найдем решение у(х) уравнения (10). Пример. Найти общее решение уравнения Будем искать решение у(х) данного линейного неоднородного уравнения в виде Подставляя исходное уравнение, получим.

Определим функцию v(x) как решение уравнения Разделяя переменные, найдем Выберем любое частое решение, например, отвечающее ) получим Для общего решения исходного уравнения получаем выражение Преимущество метода вариации постоянной заключается в том, что он переносится на линейные неоднородные дифференциальные уравнения высшего порядка. Уравнение Бернулли Некоторые дифференциальные уравнения путем замены переменных могут быть сведены к линейным.

К числу таких уравнений относится уравнение Бернуми Уравнение это предложено Я. Бернулли в 1695 г., метод решения опубликовал И. Бернулли в 1697 г. При а = 1 получаем однородное линейное уравнение При а = 0 — неоднородное линейное уравнение Поэтому будем предполагать, что (для а нецелого считаем, что у > 0). Подстановкой z = y_a+1 уравнение Бернулли приводится к линейному уравнению относительно функции z(x). Однако уравнение Бернулли можно проинтегрировать сразу методом вариации постоянной.

Это делается так. Сначала интегрируем уравнение Его общее решение Решение уравнения Бернулли будем искать в виде где С(х) — новая неизвестная функция. Подставляя это выражение для у(х) в уравнение Бернулли, получаем — уравнение с разделяющимися переменными относительно С(х). Интегрируя это уравнение, находим где С — постоянная интегрирования. Тогда из формулы получаем обший интеграл уравнения Бернулли Замечание.

При а > 0 уравнение Бернулли имеет очевидное решение у = 0. Для интегрирования уравнения Бернулли можно также воспользоваться подстановкой Некоторые виды уравнений, интегрируемых в квадратурах Уравнения с разделяющимися переменными Уравнения, однородные относительно х и у Линейные дифференциальные уравнения Уравнение Бернулли Уравнения в полных дифференциалах где в качестве берется любое нетривиальное решение уравнения а функция и(ж) определяется как решение уравнения Пример.

Уравнения в полных дифференциалах Уравнение называется уравнением в полных дифференциалах, если левая часть уравнения представляет собой полный дифференциал некоторой функции гх(ж, у) двух независимых переменных ж и у, т. е. В этом случае «(ж, у) — С будет общим интегралом дифференциального уравнения (18). Будем предполагать, что функции М(ж, у) и N(x, у) имеют непрерывные частные производные соответственно по у и по ж в некоторой односвязной области D на плоскости хОу. Теорема 4.

Для того чтобы левая часть М(ж, у) dx + N(xt у) dy уравнения (18) была полным дифференциалом некоторой функции и(х, у) двух независимых переменных х и у, необходимо и достаточно, чтобы выполнялось тождество 4 Необходимость. Предположим, что левая часть уравнения (18) есть полный дифференциал некоторой функции Дифференцируем первое соотношение по у, а второе по х: ду вудх дх дхду Отсюда, в силу равенства смешанных производных, вытекает тождество Необходимость (19) доказана.

Достаточность. Покажем, что условие (19) является и достаточным, а именно, предполагая его выполненным, найдем функцию tx(x, у) такую, что или, что то же, Найдем сначала функцию и(ху у), удовлетворяющую первому условию (20). Интегрируя это равенство по х (считаем у постоянной), получаем где произвольная функция от у. Подберем так, чтобы частная производная по у от функции и, определяемой формулой (21), была равна N(x> у). Такой выбор функции (р(у) при условии (19) всегда возможен.

В самом деле, из (21) имеем Приравняв правую часть полученного равенства к N(x, у), найдем Левая часть последнего равенства не зависит от х. Убедимся в том, что при условии (20) в его правую часть также не входит х. Для этого покажем, что частная производная по х от правой части (22) тождественно равна нулю. Имеем Теперь, интегрируя равенство (22) по у, получим, что где С — постоянная интегрирования.

Подставляя найденное значение для в формулу (21), получим искомую функцию полный дифференциал которой, как нетрудно проверить, равен Приведенный прием построения функции м(х, у) составляет метод интегрирования уравнения (18), левая часть которого есть полный дифференциал. Пример 8. Проверить, что уравнение является уравнением в полных дифференциалах, и проинтегрировать его. А В данном случае откуда Следовательно, уравнение есть уравнение в полных дифференциалах.

Можно показать, что для уравнения первого порядка при определенных условиях на функции М(х, у) и N(x, у) интегрирующий множитель всегда существует, но отыскание его из условия в общем случае сводится к интегрированию уравнения в частных производных, что составляет, как правило, задачу еще более трудную. Задача. Найти интегрирующий множитель для линейного дифференциального уравнения dy Указание. Искать множитель в виде ц = ц(х).

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник