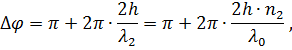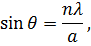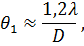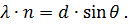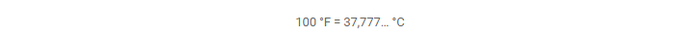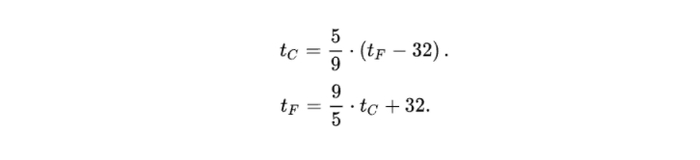Интерференция что к ней относится
Интерференция световых волн
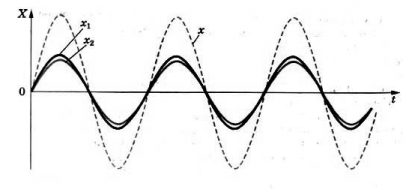
Интерференция – это одно из наиболее ярких проявлений волновой природы света. Мы можем наблюдать такое интересное и красивое явление, если наложить друг на друга 2 или более световых пучков. В месте перекрывания пучков интенсивность волны света обладает характером чередующихся светлых и темных полос, при этом в точках максимумов интенсивность больше, а в точках минимумов меньше суммы интенсивностей пучков.
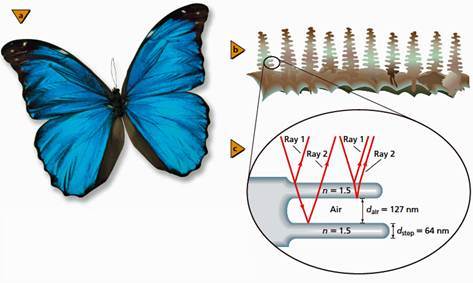
При белом свете интерференционные полосы окрашиваются в разные цвета светового спектра. На практике интерференционные явления окружают нас повсюду. Это и цвета масляных пятен на асфальте, и окрашивание замерзающих оконных стекол, и чудесные цветные рисунки на крыльях отдельных бабочек и жуков.
Первый научный эксперимент проявления интерференции света
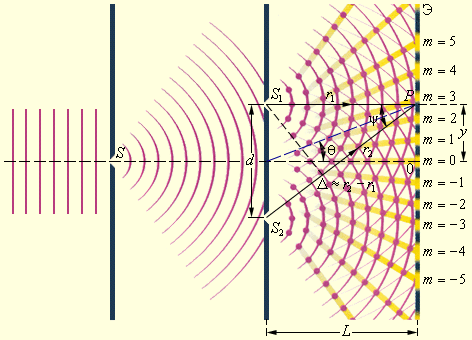
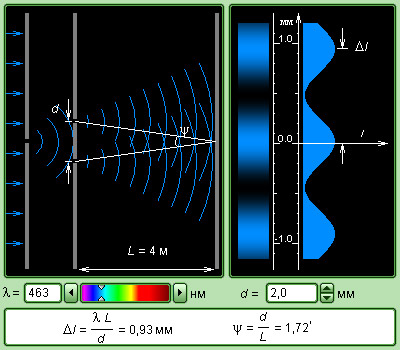
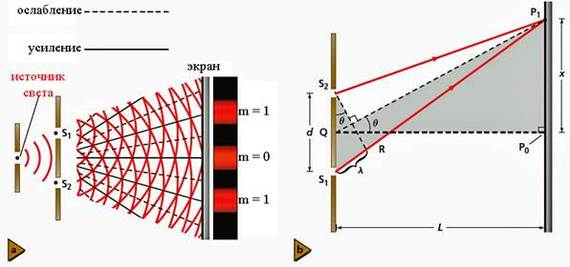
Интерференционный опыт Юнга
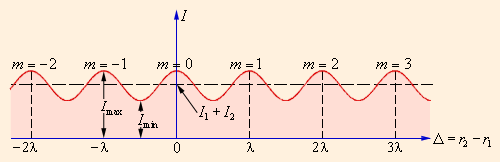
Путем простых тригонометрических вычислений можно прийти к следующему выражению для интенсивности результирующего колебания в точке P :
где Δ = r 2 – r 1 – это разность хода.
Подчеркнем, что в волновой оптике понятие “луч света” теряет физический смысл в отличие от геометрической оптики. Определение «луч» в волновой оптике употребляется для краткости обозначения направления распространения волны.
Далее данный термин будет упоминаться без кавычек.
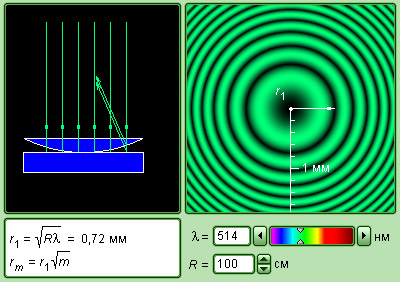
По данной формуле рассчитывается длина световой волны λ при известном радиусе кривизны R линзы.
Проблема когерентности волн
Интерференция света
теория по физике 🧲 оптика
Для всех волн характерны явления интерференции и дифракции. Если свет — это волна, то для него также должны быть присущи эти явления. Так рассуждали ученые, которые считали, что свет имеет волновую природу. Первым привел экспериментальные доказательства интерференции и дифракции света Томас Юнг в 1801 году.
Это интересно! Явление интерференции света было описано и объяснено в 1801 году, но само понятие «интерференция света» было введено немного позже — в 1803 году.
Интерференция механических волн
Чтобы лучше понять явление интерференции, сначала объясним его на примере механических волн, за которыми удобней наблюдать. Часто случается, что в среде одновременно распространяется несколько различных волн. К примеру, когда в комнате может одновременно находиться несколько источников звука. Что же происходит, когда волны пересекают друг друга? Объясним это на примере волн, образуемых на поверхности воды.
Если бросить в воду два камешка, образуются две круговые волны. Если наблюдать за их распространением, мы увидим, что каждая волна проходит сквозь другую. Причем она ведет себя так, как будто другой волны не существовало. Точно так же любое количество звуковых волн может одновременно распространяться в воздухе. И они не будут друг другу мешать. Множество музыкальных инструментов в оркестре или голосов в хоре создает звуковые волны, которые улавливаются нами одновременно. При этом звуки не сливаются в шум: наши органы слуха способны легко отличить один звук от другого.
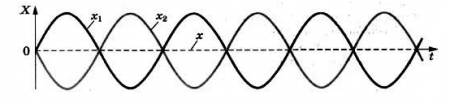
Теперь рассмотрим более подробно процесс, когда волны накладываются одна на другую. Для этого будем наблюдать волны на поверхности воды от двух брошенных в воду камней. При этом мы заметим, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если два гребня двух волн встречаются в одном месте, то в этом месте возмущение поверхности воды становится более сильным. Если же гребень одной волны встречается с впадиной другой, то поверхность воды в этом месте остается спокойной. Получается, что в каждой точке среды колебания, вызванные двумя волнами, складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.
Интерференция — сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний частиц среды.
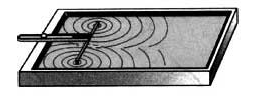
Чтобы выяснить, при каких условиях наблюдается интерференция волн, одновременно возбудим две круговые волны в ванночке с помощью двух шариков, прикрепленных к стержням, колеблющимся по гармоническому закону.
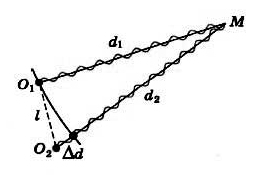
Теперь представим явление интерференции схематически. В любой точке М на поверхности воды будут складываться колебания, вызванные двумя волнами от источников O1 и O2 (см. рисунок ниже). Амплитуды колебаний, вызванных в точке М обеими волнами, будут различаться, если волны проходят различные пути d1 и d2. Но если расстояние l между источниками много меньше этих путей, то обе амплитуды можно считать приближенно одинаковыми.
Результат сложения волн, приходящих в точку М зависит от разности фаз между ними. Пройдя различные расстояния d1 и d2, волны имеют разность хода, определяемую формулой:
Когда разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой на один период. Так как за период волна проходит путь, равный ее длине волны, то в точке встречи двух волн фазы совпадают. Если в этой точке волны имеют гребни, то совпадают гребни, если впадины — совпадают впадины.
Условие минимумов и максимумов
Когда гребни волн на поверхности волны складываются в одной точке, их амплитуда резко возрастает. В этом случае говорят, что в этой точке образуется интерференционный максимум. Когда впадины волн на поверхности волны складываются в одной точке, их амплитуда резко уменьшается. В этом случае говорят, что в этой точке образуется интерференционный минимум. Интерференционные минимумы и максимумы образуются при соблюдении определенных условий.
Если разность хода волн равна нечетному числу полуволн, то в точке наложения этих волн образуется интерференционный минимум. Амплитуда колебаний в данной точке минимальна.
Если разность хода волн равна целому числу волн, то в точке наложения этих волн образуется интерференционный максимум. Амплитуда колебаний в данной точке максимальна.
Если разность хода ∆d принимает промежуточное значение между λ и λ/2, амплитуда результирующих колебаний принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но важной примечательностью является то, что амплитуда колебаний в любой точке с течением времени не меняется. Поэтому на поверхности воды возникает определенное, постоянное во времени распределение амплитуд колебаний, которое называют интерференционной картиной.
Для формирования устойчивой интерференционной картины важно, чтобы источники волн имели одинаковую частоту, и разность фаз их колебаний не менялась с течением времени. Такие источники волн называют когерентными.
Когерентные волны — это волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
Только когерентные волны при сложении формируют устойчивую интерференционную картину. Если же источники волн некогерентные, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет с течением времени изменяться. Поэтому амплитуда результирующих колебаний также будет непрерывно изменяться. В результате максимумы и минимумы в пространстве будут иметь неопределенное положение. Поэтому интерференционная картина получается размытой.
Распределение энергии при интерференции
Любая волна переносит энергию без переноса вещества. Но что же с этой энергией происходит при интерференции волн? Если волны встречаются друг с другом, энергия никуда не исчезает и не превращается в другие формы энергии. Она лишь перераспределяется таким образом, что в минимумах он не поступает совсем, поскольку концентрируется в максимумах.
Интерференция света
Ели свет — это поток волн, то должно наблюдаться явление интерференции. Однако получить интерференционную картину, при которой чередуются минимумы и максимумы с помощью двух независимых источников света (к примеру, двух ламп), невозможно. Включение второй лампы лишь увеличивает освещенность поверхности, но не создает картины из минимумов и максимумов. Это объясняется несогласованностью волн друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные, то есть когерентные световые волны. Они должны иметь одинаковые длины волн и постоянную во времени разность фаз в любой точке пространства.
Однако наблюдать интерференцию света все же можно. Вы ее наблюдали, когда пускали мыльные пузыри или рассматривали пленку нефти на поверхности воды.
Томас Юнг — первый из ученых, который предложил объяснить изменение цветов тонких пленок сложением волн. Согласно его предположению, одна волна отражается от наружной поверхности плёнки, а другая — от внутренней. При этом возникает явление, называемой интерференцией световых волн.
Усиление света происходит в том случае, если преломлённая волна запаздывает по сравнению с отражённой волной на целое число длин волн. Здесь действует условие максимумов, о котором мы говорили выше:
Если вторая волна запаздывает по сравнению с первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света. Здесь действует условие минимумов, о котором мы также уже говорили:
Четкая интерференционная картина получается потому, что волны, отраженные от внутренней и внешней оболочки тонкой пленки, являются когерентными. Когерентность этих волн объясняется тем, что они являются частями одного и того же светового луча.
Юнг сделал вывод, что многообразие цветов на мыльной пленке связано с разницей в длине волны. Если плёнка имеет неоднородную толщину, то при освещении её белым светом появляются различные цвета.
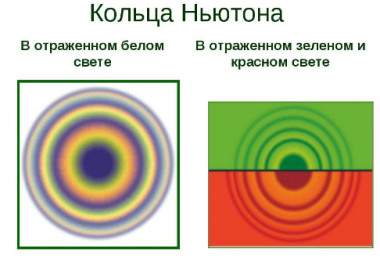
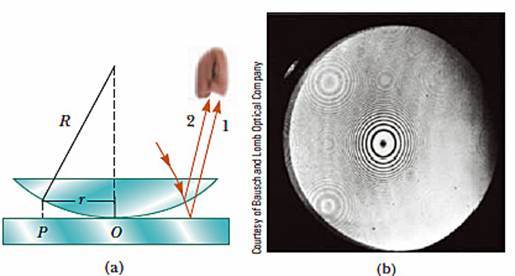
Простую интерференционную картину также можно получить, если положить на стеклянную поверхность плоско-выпуклую линзу, сферическая поверхность которой имеет большой радиус кривизны. Интерференционная картина, полученная таким способом, носит название колец Ньютона.
Исаак Ньютон исследовал интерференционную картину, получаемую в тонкой прослойке воздуха между стеклом и линзой, не только в белом свете, но и при освещении линзы монохроматическими лучами. Так он установил, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному. Так, красные кольца имеют максимальный радиус. Расстояние между соседними кольцами уменьшаются с увеличением их радиусов.
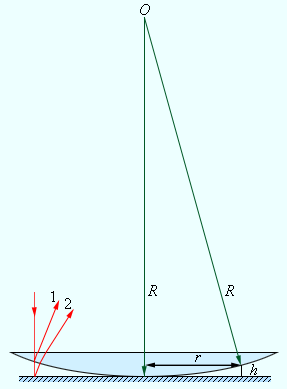
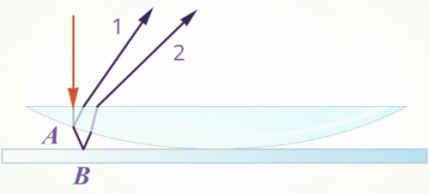
Ньютону удалось получить кольца, но их появление он объяснить не смог. Но это удалось сделать Юнгу. Проведенный им опыт показал, что волна определённой длины падает на плосковыпуклую линзу почти перпендикулярно. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе сред стекло-воздух, а волна 2 — в результате отражения от пластины на границе сред воздуха- стекло.
Если вторая волна запаздывает по сравнению с первой на целое число длин волн, то при сложении волны усиливают друг друга. Если вторая волна запаздывает по сравнению с первой на нечётное число полуволн, то колебания в точке сложения будут совпадать в противоположных фазах. При этом волны погасят друг друга.
В результате проделанного эксперимента Юнг смог получить картину, которая состоит из чередующихся параллельных полос (темных и светлых)
Интерференция света – это явление сложения двух и более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующегося максимумом и минимумом интенсивности.
Это интересно! Измеряя радиусы колец Ньютона, можно вычислить длины волн. В ходе измерений было установлено, что для красного света λкр = 8∙10 –7 м, а для фиолетового — λa = 4∙ 10 –7 м.
Пример №1. Будет ли наблюдаться интерференционная картина при освещении мыльной пленки монохроматическим светом? Какой она будет?
Поскольку источник света один и тот же, то отраженные от обеих поверхностей мыльной пленки волны будут когерентными. Поэтому интерференционная картина наблюдаться будет. Она примет вид чередующихся цветных и темных полос. Цвет полос определяется цветом световой волны, который зависит от ее длины волны.
На поверхность тонкой прозрачной плёнки падает по нормали пучок белого света. В отражённом свете плёнка окрашена в зелёный цвет. При использовании плёнки такой же толщины, но с несколько меньшим показателем преломления, её окраска будет
б) находиться ближе к красной области спектра
в) находиться ближе к синей области спектра
Интерференция и дифракция
Интерференция – это сложение колебаний. В результате интерференции в каких-то точках пространства происходит рост амплитуды колебаний, а в других – их уменьшение. Неизменная картина интерференции наблюдается только тогда, когда разность складываемых колебаний постоянна (они когерентны). Очевидно, что когерентными могут быть колебания одинаковой частоты. Поэтому чаще всего изучают интерференцию монохроматических колебаний.
На фото изображена интерференция волн на поверхности воды.
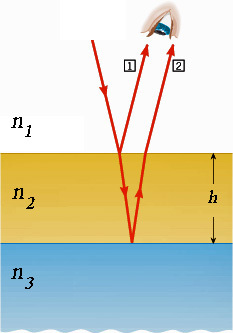
Интерференцию световых волн можно наблюдать, если положить стеклянную линзу на стеклянную пластинку (см. рисунок справа) и посмотреть на них сверху. Луч света (красные стрелки) падает сверху на линзу, преломляется, отражается от её нижней искривлённой поверхности и выходит из линзы (луч 2). Однако часть луча, упавшего на нижнюю поверхность линзы, выходит из неё, падает на стеклянную пластинку, отражается от неё, проходит через линзу и выходит из неё (луч 1). Лучи 1 и 2 когерентны, т.к. они возникли из одного луча.
Если попав в глаз, фаза этих лучей будет отличаться на целое число периодов, то эти лучи будут усиливать друг друга и мы увидим яркое пятно. В тех случаях, когда их разность фаз составит нечётное число полупериодов (Т/2, 3Т/2, 5Т/2 и т.д.) лучи уничтожат друг друга, и мы увидим тёмное пятно.
Очевидно, что разность фаз между лучами 1 и 2 зависит от толщины зазора между линзой и пластинкой. Поэтому, смотря сверху мы увидим чередующиеся тёмные и светлые кольца – кольца Ньютона (см. рисунок).
На фото ниже показаны интерференционные полосы для синего света (левая), для красного света (средняя) и для белого света (правая).
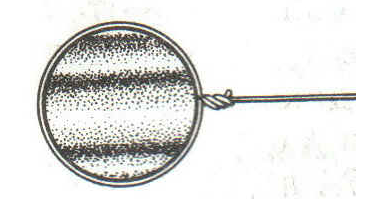
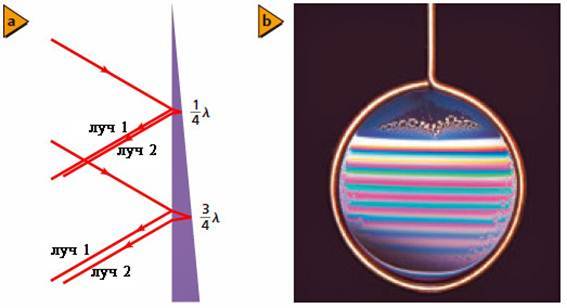
Интерференционные полосы можно наблюдать в свете, отражённом от вертикально расположенной мыльной плёнки (см. рисунок ниже). Толщина плёнки увеличивается сверху вниз, что изменяет разность хода между лучами, отражёнными от обеих поверхностей плёнки. На рисунке а схематически показан верхний красный луч, падающий слева на фиолетовую плёнку (в разрезе). Этот луч сразу отражается и получает обозначение (луч 1). Другая часть того же луча преломляется в плёнке, отражается от другой её поверхности (луч 2) и продолжает двигаться рядом с лучом 1. Если при этом разница фаз между лучами 1 и 2 станет кратной периоду колебаний, то лучи будут усиливать друг друга, и мы увидим яркую полосу. Если же эта разница фаз составит нечётное число полупериодов (Т/2, 3Т/2, 5Т/2 и т.д.), то они уничтожат друг друга, а мы увидим тёмную полосу.
Следует отметить, что волны при отражении изменяют фазу на 180° (или p), если отражаются от более оптически плотной среды, например, при отражении света в воздухе от воды. Если отражение происходит от менее оптически плотной среды, то изменение фазы волны не происходит.
где l0 – длина волны света в вакууме.
Дифракцией называют явления, связанные со свойством волн огибать препятствия, т.е отклоняться от прямолинейного распространения.
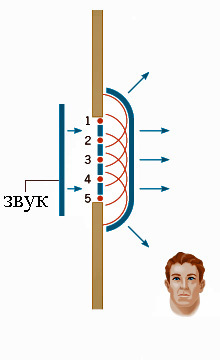
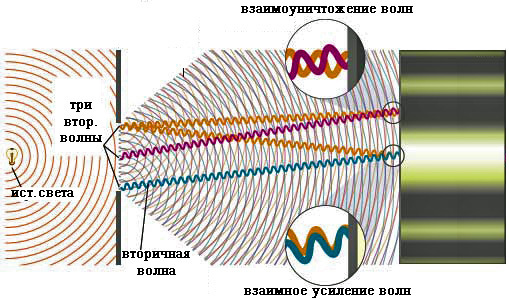
На рисунке ниже показано, как меняют направление звуковые волны после прохождения через отверстие в стене. Согласно принципа Гюйгенса области 1-5 становятся вторичными источниками сферических звуковых волн. Видно, что вторичные источники в областях 1 и 5 приводят к огибанию волнами препятствий.
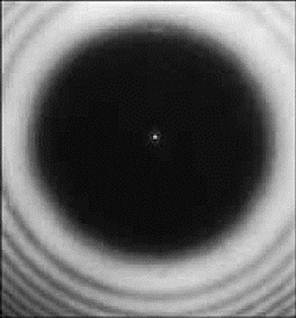
Ниже показано фото тени от монеты на экране при освещении её источником монохроматического света. Видно, что в центре тени есть яркое пятно, образованное интерференцией лучей, огибающих край монеты. Интерференция этих лучей приводит к появлению чередующихся тёмных и ярких колец, окружающих тёмный диск тени. Этот эксперимент тоже является иллюстрацией явления дифракции света.
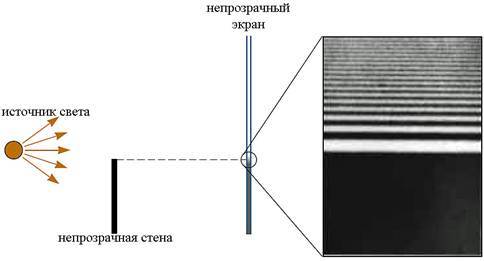
Ниже показано увеличенное фото тени верхнего края непрозрачной стены на экране. Видно, что переход из тёмной части тени в освещённую происходит не резко, а через последовательность чередующихся тёмных и ярких полос. Эти полосы являются результатом дифракции лучей света на краю препятствия и последующей их интерференции.
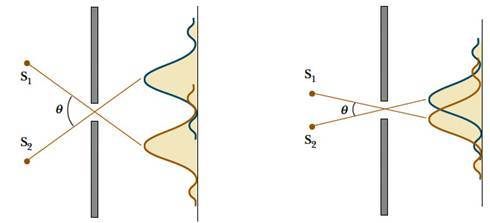
Если расстояние L до экрана, на котором наблюдают дифракционную картину, гораздо больше ширины a щели (см. рисунок ниже), то угол, под которым виден первый дифракционный минимум номер n (см. yn на рисунке), можно вычислить из соотношения
Дифракция света наблюдается, если он проходит через круглое отверстие (см. левый рисунок). При этом дифракционная картина состоит из центрального яркого пятна, окружённого чередой тёмных и ярких колец. При этом угловой диаметр q1 центрального яркого пятна равен
Таким образом, чем больше будет диаметр входной линзы или зеркала телескопа, тем больше звёзд мы увидим на небе.
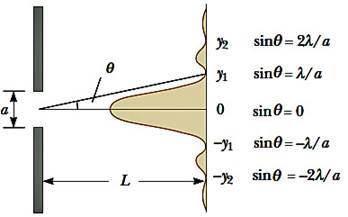
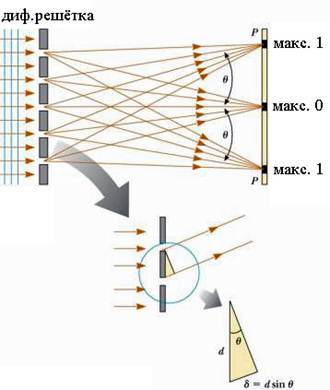
Дифракционная решётка – это прозрачная пластинка, на которую через одинаковое расстояние d (период решётки) нанесены параллельные штрихи. Плоский фронт световой волны падает слева на дифракционную решётку (см. рисунок) и претерпевает дифракцию на её штрихах. После интерференции прошедших через решётку лучей появляются направления, вдоль которых наблюдаются дифракционные максимумы и минимумы интенсивности света.
Угол qn, под которым виден первый дифракционный максимум номер n, легко вычислить, если считать, что расстояние до экрана Р гораздо больше периода решётки d:
На рисунке справа показано, как дифракционная решётка расщепляет голубой луч лазера.
Дифракционная решётка не только может отклонять лучи, как призма, но и разлагать их в спектр. Справа показано, что происходит с белым светом, после того, как он проходит через дифракционную решётку. Видно, что дифракционная картина в этом случае представляет собой наложение дифракционных картин для цветов, образующих белый свет
Явления дифракции и интерференции света помогают Природе раскрашивать всё живое, не прибегая к использованию красителей
вот те плюс за труды. хотя бы..
По первой картинке:
Что видит девушка? «Уточки!»
Что видит парень? «Утки и круги на воде»
Что видит физик? «Интерференция»
то чувство, когда нечаянно открыл пост с телефона и как сумасшедший свапаешь в низ, в поисках конца
Где же пропадал этот пост, когда я лет 8 назад отвечал такой билет на 1м курсе?
Ладно, ладно, начну я готовиться к физике
как увидишь над пашнею радугу,
атмосферы родимой явление,
и застынешь в немом изумлении,
очарован внезапною прелестью,
и стоишь, очарованный прелестью.
Тем, кто в 21 веке квантмех геометрической оптикой объясняет нужно вместо машин выдавать паровые повозки.
Молодец! Закинул в наш темный колодец такой матан (понятно что не матан).
А уточки на первом фото на батарейках?
Блять, я на 1 картинке увидел член из волн.
Правда ли, что Фаренгейт принял за 100 градусов температуру тела своей больной жены?
Согласно распространённой версии, немецкий естествоиспытатель собирался зафиксировать важную отметку на своей шкале на уровне нормальной температуры человеческого тела. Однако у его супруги в этот момент был жар, из-за чего сегодня 100 °F соответствует 37,8 °C. Мы проверили, насколько правдоподобна эта легенда и разобрались в истории появления температурных делений.
(Спойлер для ЛЛ: неправда)
Контекст. Шкала Фаренгейта — одна из основных температурных шкал, которая используется в ряде стран мира, в частности в США. Вот что сообщает об истории её появления портал newtonov.ru, помогающий школьникам в изучении физики:
«В своей шкале Фаренгейт использовал не две, а три основные реперные точки. За ноль была принята температура замерзания смеси льда, воды и нашатыря, которая, по одной из версий, соответствовала температуре самого холодного дня зимы 1709 года. Вторая точка — это температура замерзания воды. Она заняла отметку в 32°. И третьей точкой, в 100°, должна была стать температура здорового человека. Но то ли 300 лет назад люди были более горячие, то ли Фаренгейт что-то намерил неправильно.
В общем, 100 °F — это температура не здорового человека, а самого что ни на есть больного. Существует версия, согласно которой за эталон температуры здорового человека Фаренгейт взял температуру своей жены. Но на тот момент она приболела, и получилось то, что получилось».
Если воспользоваться онлайн-калькулятором для перевода градусов Фаренгейта в более привычные нам градусы Цельсия, то получим следующий результат:
То есть, действительно, если версия с температурой тела как мотивом истинна, то эталоном для Фаренгейта должен был послужить не совсем здоровый человек. Ознакомимся с историей появления его изобретения поподробнее.
Даниэль Габриэль Фаренгейт родился в 1686 году в Данциге (нынешнем Гданьске) в немецкой семье. С юных лет он проявил интерес к естественнонаучным экспериментам, и позднее, когда уже обосновался в Нидерландах, изготовил термометр и барометр. Сначала термоскопической жидкостью ему служил спирт, однако около 1714 года он заменил спирт ртутью, чем достиг гораздо большей точности измерений. Наконец, в 1724 году он предложил принципиально новую шкалу, которая станет стандартом в англоязычных странах для метеорологических, промышленных и медицинских целей на следующие два с половиной века. Для перевода температуры по этой шкале в градусы Цельсия и обратно используются следующие формулы:
Многие люди, впервые сталкивающиеся с ними, сетуют на неудобство подобного преобразования. Однако шкала Цельсия была предложена на 18 лет позже, в 1742 году, то есть вопросы в данном случае должны быть обращены не к Фаренгейту.
Итак, что мы знаем сегодня о трёх калибровочных точках шкалы Фаренгейта?
Задумавшись о подходящей разметке для своего будущего термометра, Фаренгейт в 1708 году посетил пожилого датского астронома Оле Рёмера (не путать с Реомюром), который разработал собственную шкалу. Следует отметить, что у Рёмера температура кипения воды равнялась 60 градусам, за ноль была взята температура очень холодной зимы в Дании, вода замерзала при 7,5 градуса, а нормальная температура тела составляла 22,5 градуса.
Много лет спустя в письме к другому физику Фаренгейт расскажет об этом своём визите:
«Я застал его [Рёмера] ранним утром, он поместил термометры в воду со льдом. Позднее он помещал их в воду с температурой тела. После того как он отметил эти две точки на всех термометрах, он добавил половину расстояния меж точек ниже точки со льдом и поделил получившийся отрезок на 22,5 равной части, начиная с нуля. 7,5 градуса — на точке со льдом и 22,5 на температуре тела. Я использовал эту градуировку вплоть до 1717 года с тем лишь отличием, что разделил каждый градус ещё на четыре части. Эта градуировка очень неудобна из-за дробей, поэтому я решил поменять шкалу и использовать 96 вместо 22,5 или 90, с тех пор я использую её».
Таким образом, за базу своей шкалы Фаренгейт взял разработку Оле Рёмера, однако для удобства умножил некоторые (но не все, как мы убедимся далее) числа на 4. При этом уже в описании шкалы датчанина упоминается некая «температура тела». Однако это не даёт точного ответа на вопрос о калибровочных точках. В своей публикации 1724 года Фаренгейт пишет, что в его шкале таковых используется три: максимально низкая температура смеси льда, воды и нашатыря или даже морской соли» (0 °F), температура таяния льда (32 °F) и температура тела (96 °F). Однако это не совсем корректное сообщение. Как отмечают современные учёные, в первом случае можно получить +5 °F или даже –8 °F (в случае морской соли), то есть это даже не одна и та же величина, не говоря уже о несоответствии нулю. Возможно, права легенда о том, что за ноль было взято положение столбика в аномально холодную зиму 1708–1709 годов в Данциге (а не в Дании).
После смерти Фаренгейта его шкала немного поменялась. В 1776 году комиссия Лондонского Королевского общества во главе с Генри Кавендишем приняла решение откалибровать шкалу так, чтобы вода замерзала ровно при 32 °F, а кипела, соответственно, при 212 °F (расстояние в 180 градусов — круглое число, особенно для градусов). Так что сегодня «нормальная температура тела» составляет не 96 °F, как при Фаренгейте (сейчас это было бы равно 35,56 °С), а 97,88 °F (в подмышечной впадине) и 98,6 °F (во рту).
Да, и, наконец, о жене Даниэля Фаренгейта. Увы, увлечённый своими опытами, за всю свою жизнь он так ни разу и не женился.