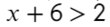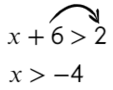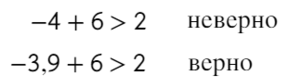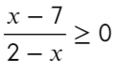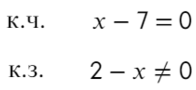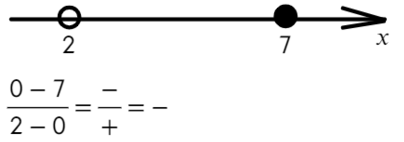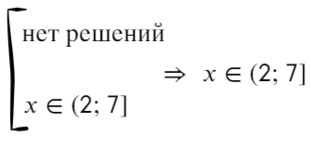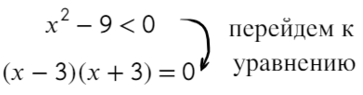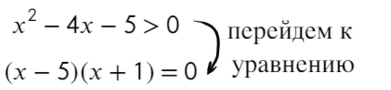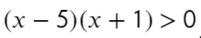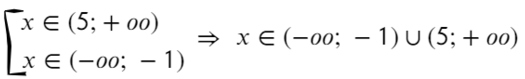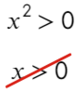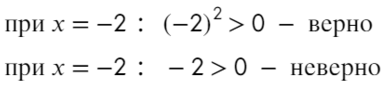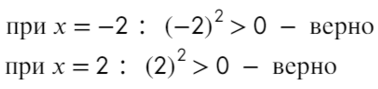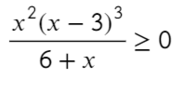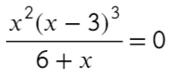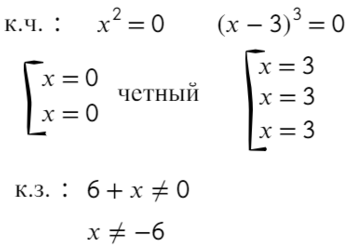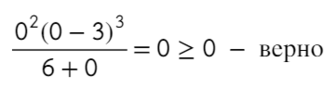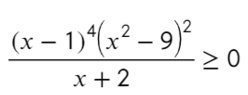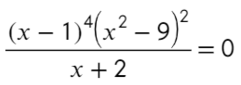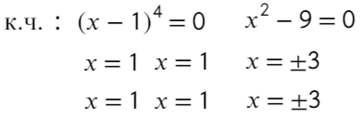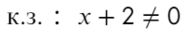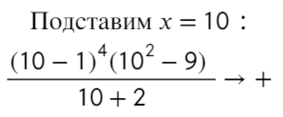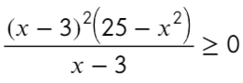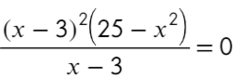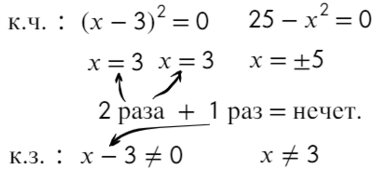Интервал и отрезок в чем разница
Закрашенная и незакрашенная точка
Знание — сила. Познавательная информация
Выколотая точка или закрашенная?
Эта ассоциация поможет легко запомнить, выколотая точка или закрашенная на числовой прямой.
Сравните неравенства, при которых точка заштрихована: x≥a или x≤b и неравенства, в которых точка выколотая: x>a, x или Светлана Иванова, 27 Сен 2012
Сегодня мы узнаем, как использовать метод интервалов для решения нестрогих неравенств. Во многих учебниках нестрогие неравенства определяются следующим образом:
— это неравенство вида которое равносильно совокупности строгого неравенства и уравнения:
В переводе на русский язык это значит, что нестрогое неравенство это объединение классического уравнения и строгого неравенства Другими словами, теперь нас интересуют не только положительные и отрицательные области на прямой, но и точки, где функция равна нулю.
Отрезки и интервалы: в чем разница?
Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:
Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:
На этом рисунке отмечен отрезок и интервал Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые.
Метод интервалов для нестрогих неравенств
К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:
Задача. Решите строгое неравенство:
Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:
Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:
Задача. Решите нестрогое неравенство:
Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:
Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:
Итак, основное отличие строгих и нестрогих неравенств:
Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.
Почему бесконечности всегда стоят в круглых скобках
У внимательного читателя наверняка возник вопрос: почему бесконечности отмечаются круглыми скобками даже в нестрогих неравенствах? Например, почему в последней задаче мы пишем
Что ж, это не опечатка. Бесконечность действительно обозначается круглой скобкой, даже если неравенство — нестрогое. Чтобы понять, почему так происходит, достаточно вспомнить определение бесконечности.
— это гипотетическое число, которое больше любого другого числа, участвующего в решении.
Трудность заключается в том, что нельзя работать с бесконечностью напрямую. Мы можем лишь приблизиться к ней, подставляя такие зверские числа, как 1 000 000 и даже 1 000 000 000. Но добраться до самой бесконечности все равно нельзя.
Именно поэтому бесконечность обозначают круглыми скобками. Ведь хотя бесконечность и ограничивает всю числовую прямую, сама она не принадлежит этой прямой.
Ситуация такая же, как с границами интервалов. Рассмотрим все числа из интервала:
Эта запись означает, что число не принадлежит интервалу, однако любое число, которое больше нуля и меньше единицы — принадлежит. В частности, этому интервалу принадлежат следующие числа:
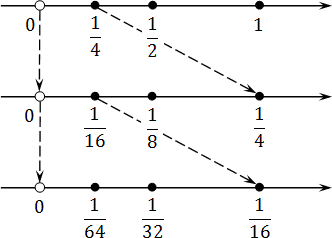
Попробуем отметить эти числа на координатной прямой. Поскольку каждое следующее число вдвое меньше предыдущего, нам придется несколько раз менять масштаб. Получим вроде этого:
Что дает нам этот график? Оказывается, при достаточно крупном масштабе можно отметить любое число, сколь угодно близкое к нулю. При этом сам ноль никуда не денется — он остается недостижимой границей. Именно это и подразумевается, когда речь заходит о концах интервала.
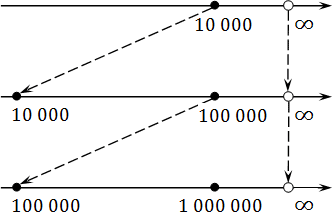
То же самое происходит и с бесконечностью. Разница лишь в том, что масштаб надо не увеличивать, а уменьшать:
Мы можем сколь угодно долго идти к бесконечности, но так и не достигнем ее. Вот почему бесконечности обозначают круглыми скобками, подобно границам интервала.
Примеры решения неравенств
В заключение кратко разберем два нестрогих неравенства. И если в первой задаче еще есть пояснения, то вторая задача будет оформлена именно так, как и надо оформлять настоящее решение.
Как обычно, приравниваем все к нулю:
( x + 8)( x − 3) = 0;
x + 8 = 0 ⇒ x = −8;
x − 3 = 0 ⇒ x = 3.
Теперь рассматриваем функцию, которая находится в левой части неравенства:
Подставим в эту функцию бесконечность — получим выражение вида:
Чертим координатную ось, отмечаем корни и расставляем знаки:
Поскольку мы решаем неравенство или, что то же самое, осталось записать ответ:
x (12 − 2 x )(3 x + 9) ≥ 0
x (12 − 2 x )(3 x + 9) = 0;
x = 0;
12 − 2 x = 0 ⇒ 2 x = 12 ⇒ x = 6;
3 x + 9 = 0 ⇒ 3 x = −9 ⇒ x = −3.
x ≥ 6 ⇒ f ( x ) = x (12 − 2 x )(3 x + 9) → (+) · (−) · (+) = (−) x ∈ (−∞ −3] ∪ [0; 6].
 Решение неравенств
Решение неравенств
Метод интервалов
Перенос знаков
Выбор точек
Система и совокупность
Точка знакопостоянства
Что нельзя делать в неравенстве, даже под пытками:
1) Домножать на знаменатель.
2) Умножать/делить на отрицательное число, не меняя знак.
3) Убирать бездумно логарифм или основание.
Линейные уравнения решаются обычным переносом. Икс в одной части оставим, а числа перенесем в другую:
А само значение −4 нам подходит?
Нет, поэтому ставим круглые скобочки ()
Разберемся со скобками:
Когда мы включаем точку (корень числителя), или стоят знаки нестрогие ( ≥, ≤ ), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,
Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:
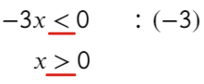
Следующий пример уже с дробью:
Приравняем числитель к нулю и скажем, что знаменатель не равен нулю:
к.ч. (корни числителя)
к.з. (корни знаменателя)
Расставляем корни числителя и знаменателя на одной прямой (сколько решаем неравенств, столько же чертим прямых). Попробуем подставить х = 0, чтобы определить знаки:
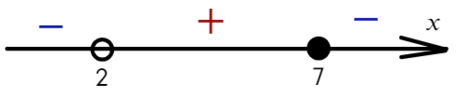
Там, где «0» (перед двойкой), ставим знак «−», а дальше знаки чередуем:
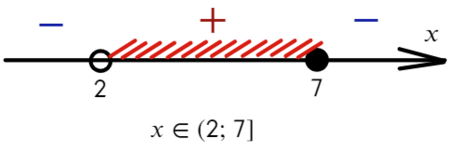
Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка:
Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,
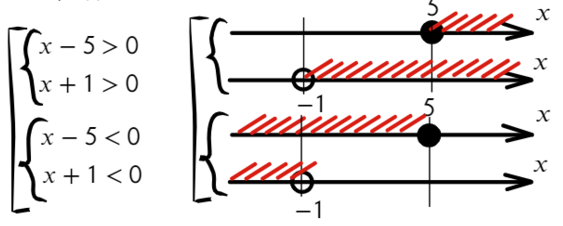
Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности:
Отметим на прямой решение каждого неравенства.
Решением совокупности «[» является тот участок, который включен хотя бы в одно неравенство.
Мой любимый пример:
Покажу мастер-класс, как делать не надо. Дома не повторять!
А теперь через метод интервалов разберемся, как сделать правильно:
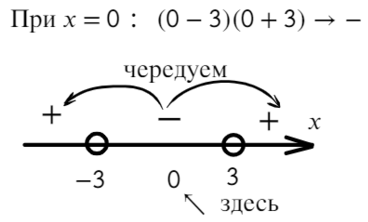
Там, где ноль, ставим знак «−», рисуем прямую и отмечаем корни каждой скобки. А дальше чередуем:
В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».
Перейдем к квадратному уравнению:
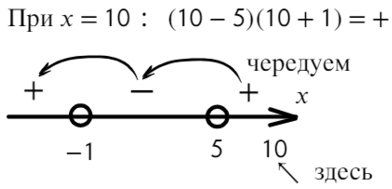
Разложим на множители и подставим x = 10, чтобы определить знак:
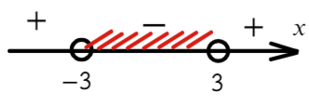
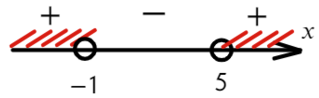
Нам требуются положительные значения:
Второй способ разложить на множители:
Ответ: x ∈ (−oo; −1) ∪ (5; +oo).
А теперь простой, но крайне показательный пример:
Убирать квадрат ни в коем случае нельзя. Простенький контрпример:
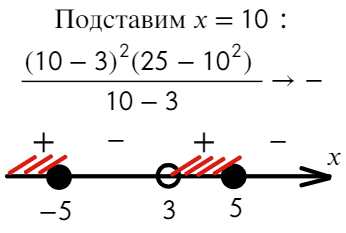
Надеюсь, убедил. Вместо знака больше поставим знак равно и попробуем решить методом интервалов:
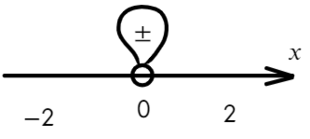
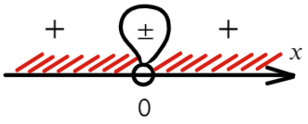
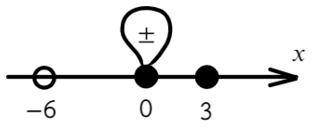
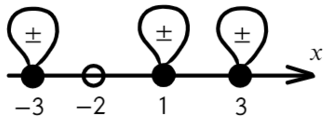
Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).
В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».
Только точка «0» не подходит, 0 > 0 — неверно!
Ответ: x ∈ R или x ∈ ( − oo; 0) ∪ (0; +oo).
Переходим на новый уровень:
Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)
По методу координат найдем корни числителя и знаменателя:
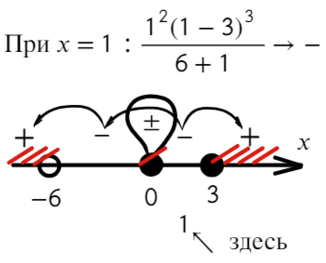
Отметим все корни на одной прямой (сколько неравенств, столько же и прямых). Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота (на ноль делить нельзя).
Требуется найти промежутки, где выражение больше или равно нулю. Нам подойдут все «промежутки», где знак плюс. Для этого подставим значение x = 1 и с промежутка [0; 3] начнем расставлять знаки. Там же находится единица.
Вот для чего ставят в восклицательном знаке ±: чтобы не потерять отдельные точки, в данном случае 0.
Ответ: (−oo; − 6) ∪ ∪ [ 3; +oo).
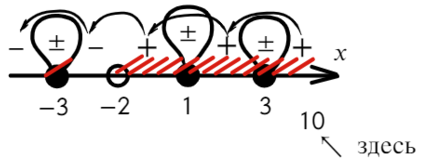
По той же схеме корни числителя и знаменателя:
Определим знак при x = 10 и расставим знаки с промежутка, где присутствует 10:
Все точки от − 2 закрашены, значит эти промежутки можно объединить в один.
Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя?
Подставим x = 10 и расставим знаки:
Ответ: [ −oo; −5) ∪ [ 3; 5).
Все скользкие моменты разобрали, стало понятнее?
Группа с полезной информацией и легким математическим юмором.
Метод интервалов: случай нестрогих неравенств
Сегодня мы узнаем, как использовать метод интервалов для решения нестрогих неравенств. Во многих учебниках нестрогие неравенства определяются следующим образом:
— это неравенство вида которое равносильно совокупности строгого неравенства и уравнения:
В переводе на русский язык это значит, что нестрогое неравенство это объединение классического уравнения и строгого неравенства Другими словами, теперь нас интересуют не только положительные и отрицательные области на прямой, но и точки, где функция равна нулю.
Отрезки и интервалы: в чем разница?
Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:
Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:
На этом рисунке отмечен отрезок и интервал Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые.
Метод интервалов для нестрогих неравенств
К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:
Задача. Решите строгое неравенство:
Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:
Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:
Задача. Решите нестрогое неравенство:
Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:
Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:
Итак, основное отличие строгих и нестрогих неравенств:
Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.
Почему бесконечности всегда стоят в круглых скобках
У внимательного читателя наверняка возник вопрос: почему бесконечности отмечаются круглыми скобками даже в нестрогих неравенствах? Например, почему в последней задаче мы пишем
Что ж, это не опечатка. Бесконечность действительно обозначается круглой скобкой, даже если неравенство — нестрогое. Чтобы понять, почему так происходит, достаточно вспомнить определение бесконечности.
— это гипотетическое число, которое больше любого другого числа, участвующего в решении.
Трудность заключается в том, что нельзя работать с бесконечностью напрямую. Мы можем лишь приблизиться к ней, подставляя такие зверские числа, как 1 000 000 и даже 1 000 000 000. Но добраться до самой бесконечности все равно нельзя.
Именно поэтому бесконечность обозначают круглыми скобками. Ведь хотя бесконечность и ограничивает всю числовую прямую, сама она не принадлежит этой прямой.
Ситуация такая же, как с границами интервалов. Рассмотрим все числа из интервала:
Эта запись означает, что число не принадлежит интервалу, однако любое число, которое больше нуля и меньше единицы — принадлежит. В частности, этому интервалу принадлежат следующие числа:
Попробуем отметить эти числа на координатной прямой. Поскольку каждое следующее число вдвое меньше предыдущего, нам придется несколько раз менять масштаб. Получим вроде этого:
Что дает нам этот график? Оказывается, при достаточно крупном масштабе можно отметить любое число, сколь угодно близкое к нулю. При этом сам ноль никуда не денется — он остается недостижимой границей. Именно это и подразумевается, когда речь заходит о концах интервала.
То же самое происходит и с бесконечностью. Разница лишь в том, что масштаб надо не увеличивать, а уменьшать:
Мы можем сколь угодно долго идти к бесконечности, но так и не достигнем ее. Вот почему бесконечности обозначают круглыми скобками, подобно границам интервала.
Примеры решения неравенств
В заключение кратко разберем два нестрогих неравенства. И если в первой задаче еще есть пояснения, то вторая задача будет оформлена именно так, как и надо оформлять настоящее решение.
Как обычно, приравниваем все к нулю:
( x + 8)( x − 3) = 0;
x + 8 = 0 ⇒ x = −8;
x − 3 = 0 ⇒ x = 3.
Теперь рассматриваем функцию, которая находится в левой части неравенства:
Подставим в эту функцию бесконечность — получим выражение вида:
Чертим координатную ось, отмечаем корни и расставляем знаки:
Поскольку мы решаем неравенство или, что то же самое, осталось записать ответ:
x (12 − 2 x )(3 x + 9) ≥ 0
x (12 − 2 x )(3 x + 9) = 0;
x = 0;
12 − 2 x = 0 ⇒ 2 x = 12 ⇒ x = 6;
3 x + 9 = 0 ⇒ 3 x = −9 ⇒ x = −3.
x ≥ 6 ⇒ f ( x ) = x (12 − 2 x )(3 x + 9) → (+) · (−) · (+) = (−) x ∈ (−∞ −3] ∪ [0; 6].
Числовые промежутки. Контекст. Определение
Введём понятие числового промежутка. Среди числовых множеств, то есть множеств, объектами которых являются числа, выделяют так называемые числовые промежутки. Их ценность в том, что очень легко вообразить множество, соответствующее указанному числовому промежутку, и наоборот. Поэтому с их помощью удобно записывать множество решений неравенства. Тогда как множеством решения уравнения будет не числовой промежуток, а просто несколько чисел на числовой прямой, с неравенствами, иначе говоря, любыми ограничениями значения переменной появляются числовые промежутки.
— это множество всех точек числовой прямой, ограниченное данным числом или числами (точками на числовой прямой).
Числовой промежуток любого вида (множество значений x, заключённых между некоторыми числами) всегда можно представить тремя видами математических обозначений: специальными обозначениями промежутков, цепочками неравенств (одним неравенством или двойным неравенством) или геометрически на числовой прямой. По сути, все эти обозначения имеют один смысл. Они дают ограничение(-я) для значений какого-то математического объекта, переменной величины (некоторой переменной, любого выражения с переменной, функции и т.д.).
Из вышесказанного можно понять, что так как можно по-разному ограничить область числовой прямой (есть разные типы неравенств), то и типы числовых промежутков бывают разные.
Виды числовых промежутков
Каждый тип числового промежутка имеет собственное название, особое обозначение. Для обозначения числовых промежутков используют круглую и квадратную скобку. Круглая скобка означает, что конечная, определяющая границу, точка на числовой прямой (конец) у этой скобки не входит во множество точек данного промежутка. Квадратная скобка означает, что конец входит в промежуток. С бесконечностью (с этой стороны промежуток не ограничен) используют круглую скобку. Иногда вместо круглых скобок можно писать квадратные, повёрнутые в обратную сторону: (a;b) ⇔]a;b[
С помощью промежутков в математике обозначается очень большое количество вещей: есть промежутки изоляции при решении уравнений, промежутки интегрирования, промежутки сходимости рядов. Промежутками принято всегда обозначать при при исследовании функции её область значений и область определения. Промежутки очень важны, например, есть теорема Больцано — Коши (можно узнать больше в «Википедии»).
Системы и совокупности неравенств
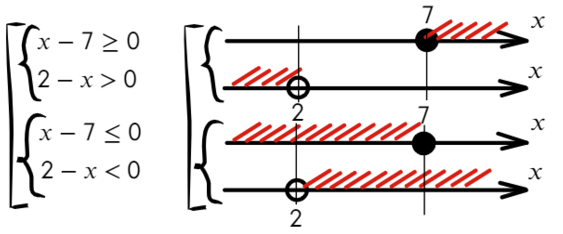
Система неравенств
Любую систему можно решать графически с использованием числовой прямой. Там, где решения составляющих систему неравенств пересекаются и будет решение самой системы.
Представим для каждого случая графическое решение.
Далее, системы неравенств можно классифицировать как равносильные, если они имеют общее множество решений. Отсюда (как можно видеть выше) следует, что более сложные системы можно упрощать (например, используя геометрическое решение).
Фигурную скобку можно условно, грубо говоря, назвать эквивалентом союза «И» для неравенств
Совокупность неравенств
Итак, все неравенства в совокупности объединяют скобкой совокупности «[«. Если значение переменной удовлетворяет хотя бы одному неравенству из совокупности, то оно принадлежит множеству решений всей совокупности. Также и с уравнениями (опять же их можно назвать частным случаем).
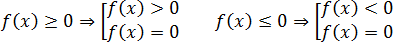

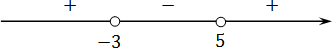
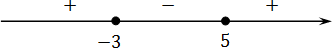
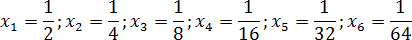
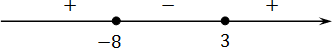
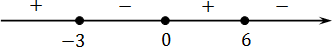
 Решение неравенств
Решение неравенств