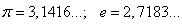Иррациональные и рациональные числа в чем отличие
Числа: натуральные, целые, рациональные, иррациональные, действительные
Натуральные числа
Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:
Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.
Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:
с — это всегда натуральное число.
Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:
с — это всегда натуральное число.
Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.
Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b
где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.
Делитель натурального числа — это натуральное число, на которое первое число делится нацело.
Каждое натуральное число делится на единицу и на себя.
Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.
Единицу не считают простым числом.
Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:
Единицу не считают составным числом.
Множество натуральных чисел составляют единица, простые числа и составные числа.
Множество натуральных чисел обозначается латинской буквой N.
Свойства сложения и умножения натуральных чисел:
переместительное свойство сложения
сочетательное свойство сложения
переместительное свойство умножения
сочетательное свойство умножения
распределительное свойство умножения
Целые числа
Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.
Числа, противоположные натуральным — это целые отрицательные числа, например:
Множество целых чисел обозначается латинской буквой Z.
Рациональные числа
Рациональные числа — это целые числа и дроби.
Любое рациональное число может быть представлено в виде периодической дроби. Примеры:
Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.
Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:
Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.
Множество рациональных чисел обозначается латинской буквой Q.
Подробнее о рациональных числах в разделе Рациональные числа.
Иррациональные числа
Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:
Подробнее об иррациональных числах в разделе Иррациональные числа.
Действительные числа
Действительные числа – это все рациональные и все иррациональные числа.
Множество действительных чисел обозначается латинской буквой R.
Разница между рациональными числами и иррациональными числами
Главное отличие
Основное различие между рациональными числами и иррациональными числами состоит в том, что рациональные числа могут быть записаны в дробной форме, тогда как иррациональные числа не могут быть записаны в дробной форме, где знаменатель и числитель не равны нулю.
Рациональные числа против иррациональных чисел
Арифметические значения или математические числа делятся на различные группы и категории по своим характеристикам и характеристикам. Основные категории включают целые числа, действительные числа, натуральные числа, рациональные числа, иррациональные числа и т. Д. Основное различие между рациональными числами и иррациональными числами включает в себя полные квадраты рациональных чисел в отличие от случайных значений иррациональных чисел. Рациональные числа можно записать в дробной форме, но иррациональные числа никогда нельзя выразить дробью. После десятичного разложения иррациональные числа дают бесконечные и неповторяющиеся значения, тогда как рациональные числа имеют повторяющиеся и конечные значения. Рациональные числа и иррациональные числа — две основные категории чисел в целом.
Числитель и знаменатель дробной формы рациональных чисел обязательно являются целыми числами. Другими словами, мы также можем сказать, что числа, которые могут быть выражены как отношение двух целых чисел, называются рациональными числами. В отличие от иррациональных чисел, рациональные числа представляют собой точные квадраты чисел, и они обладают повторяющимся или конечным числом значений после записи в десятичной форме. С другой стороны, иррациональные числа по своей природе противоположны рациональным числам. Иррациональные числа никогда не могут быть записаны в дробной форме, и они также не могут быть выражены как отношение между двумя целыми числами. Хотя иррациональные числа могут быть записаны в десятичной форме, после десятичного разложения они всегда дают бесконечные и неповторяющиеся значения.
Сравнительная таблица
| Рациональное число | Иррациональные числа |
| Рациональное число — это число, которое можно записать как отношение двух целых чисел или число, которое может быть выражено в дробной форме. | Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел или число, которое не может быть выражено в дробной форме. |
| Вовлекает | |
| Рациональные числа включают точные квадраты и конечные десятичные значения. | Иррациональные числа включают в себя значения surd и бесконечные десятичные значения. |
| Десятичное расширение | |
| Рациональные числа имеют конечные и повторяющиеся значения после десятичного разложения. | Иррациональные числа имеют бесконечные и неповторяющиеся значения после десятичного разложения. |
| Дробная часть | |
| Рациональные числа можно выразить в дробной форме. | Иррациональные числа нельзя записывать в дробной форме. |
| Целые числа | |
| Все целые числа по своей природе являются рациональными числами. | Не все целые числа по своей природе являются иррациональными. |
Что такое рациональные числа?
Рациональное число — это число, которое можно записать как отношение двух целых чисел или число, которое может быть выражено в дробной форме. Все целые числа по своей природе являются рациональными числами. Рациональные числа могут быть выражены в дробной форме, где знаменатель не равен 0, а числитель и знаменатель являются целыми числами. Рациональные числа имеют конечные и повторяющиеся значения после десятичного разложения. Рациональные числа включают точные квадраты и конечные десятичные значения. Конечные и повторяющиеся десятичные значения рациональных чисел сами по себе рациональны.
Примеры
Что такое иррациональные числа?
Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел или число, которое не может быть выражено в дробной форме. Не все целые числа по своей природе являются иррациональными. Иррациональные числа нельзя записывать в дробной форме. Иррациональные числа включают в себя значения surd и бесконечные десятичные значения. Иррациональные числа имеют бесконечные и неповторяющиеся значения после десятичного разложения. Бесконечные и неповторяющиеся десятичные значения иррациональных чисел сами по себе иррациональны.
Примеры
Ключевые отличия
Заключение
Рациональные числа — это числа, которые используются для отображения соотношения между двумя целыми числами, могут быть записаны в дробной форме, давать точные квадраты и иметь конечные и повторяющиеся значения при десятичном разложении. С другой стороны, иррациональные числа — это числа, которые не могут быть выражены в дробной форме, не отображают отношения между двумя целыми числами, дают значения surd и после десятичного разложения дают одноразовые и бесконечные значения.
Рациональные и иррациональные числа. Множество действительных чисел
Понятие рационального числа
Примеры рациональных чисел:
Любое рациональное число представимо в виде конечной или периодической бесконечной десятичной дроби.
Алгоритм перевода десятичной периодической дроби в обыкновенную дробь
Для смешанной периодической дроби – в знаменателе записать столько девяток, сколько цифр в периоде и справа дописать столько нулей, сколько цифр в дробной части до периода.
Шаг 3. Если необходимо, сократить полученную дробь
Чистые периодические дроби:
Смешанные периодические дроби:
Иррациональные числа
Примеры иррациональных чисел:
Множество иррациональных чисел не замкнуто относительно операции сложения.
Мера иррациональности действительного числа a – действительное число μ, которое показывает, насколько хорошо число a может быть приближено рациональными числами.
$μ(a) = 1 \iff a$ – рациональное число
Для многих трансцендентных чисел мера иррациональности неизвестна, есть только верхняя оценка.
Алгебраические и трансцендентные числа
Если действительное число является корнем уравнения вида
Алгебраические числа бывают рациональными и иррациональными.
Примеры трансцендентных чисел:$ π,2^<\sqrt2>, sin10^0, e^4$
Все трансцендентные числа иррациональны.
Т.е., трансцендентных чисел «больше», чем алгебраических. Их слишком много, чтобы можно было представить в виде последовательности.
Структура множества действительных чисел
Из-за несовпадения подмножеств, структуру множества действительных чисел можно представить двумя равносильными схемами:
Множество действительных чисел несчётно.
Множество действительных чисел замкнуто относительно операций сложения, вычитания, умножения и деления (исключая деление на 0).
В алгебре говорят, что действительные числа образуют непрерывное упорядоченное поле.
Примеры
Пример 1. Найдите рациональные дроби, равные данным бесконечным периодическим десятичным дробям:
Математика
Тестирование онлайн
Натуральные числа
Это числа, которые используются при счете: 1, 2, 3. и т.д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Иррациональные числа
Бесконечная непериодическая дробь называется иррациональным числом. Например:
Множество иррациональных чисел обозначается J.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.
Округление чисел
Округлить 8,759123. с точностью до целой части.
Округлить 8,759123. с точностью до десятой части.
Округлить 8,759123. с точностью до сотой части.
Округлить 8,759123. с точностью до тысячной части.
Рациональное и иррациональное число: описание и чем они отличаются?
Откуда же произошли следующие термины такие, как:
А свои корни они извлекли из латинского слова «ratio», что означает «разум». Исходя из дословного перевода:
Общее понятие рационального числа
Рациональным числом считается то число, которое можно записать в виде:
Иными словами, к рациональному число подойдет следующие определения:
Примеры рационального числа
Рассмотрим примеры рациональных чисел:
Из вышеперечисленных примеров совершенно очевидно, что рациональные числа могут быть как положительными так и отрицательными. Естественно, число 0 (нуль), которое тоже в свою очередь является рациональным числом, в тоже время не относится к категории положительного или отрицательного числа.
Общее понятие и определение иррационального числа
Помимо «рациональных чисел» нам известны и так называемые «иррациональные числа». Вкратце попробуем дать определение данным числам.
Еще древние математики, желая вычислить диагональ квадрата по его сторонам, узнали о существовании иррационального числа.
Исходя из определения о рациональных числах, можно выстроить логическую цепь и дать определение иррациональному числу.
Итак, по сути, те действительные числа, которые не являются рациональными, элементарно и есть иррациональными числами.
Десятичные дроби же, выражающие иррациональные числа, не периодичны и бесконечны.
Примеры иррационального числа
Рассмотрим для наглядности небольшой пример иррационально числа. Как мы уже поняли, бесконечные десятичные непериодические дроби называются иррациональными, к примеру:
Вообще все действительные числа являются как рациональными так и иррациональными. Говоря простыми словами, иррациональное число нельзя представить ввиде обыкновенной дроби х/у.
Общее заключение и краткое сравнение между числами
Мы рассмотрели каждое число по отдельности, осталось отличие между рациональным числом и иррациональным:
Заключим нашу статью несколькими определениями: