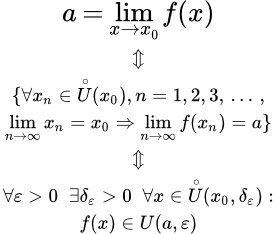Используя определение предела доказать что lim

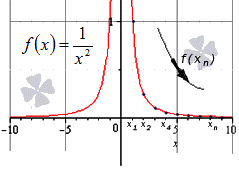
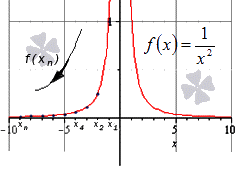
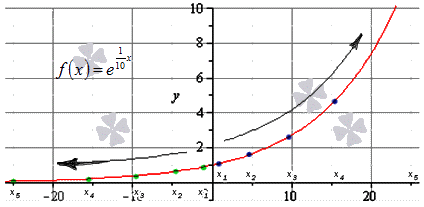
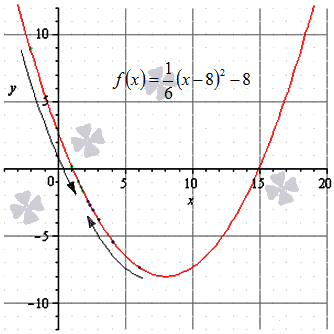
Два определения предела функции и их эквивалентность.

Определение предела по Коши.

Число \(A\) называется пределом функции \(f(x)\) в точке \(a\), если эта функция определена в некоторой окрестности точки \(a\), за исключением, быть может, самой точки \(a\), и для каждого \(\varepsilon>0\) найдется число \(\delta>0\) такое, что для всех \(x\), удовлетворяющих условию \(|x-a| 0\ \exists\delta>0:\ \forall x:0 0\ \exists\delta>0:\ \forall x\in\dot_<\delta>(a)\rightarrow f(x)\in U_<\varepsilon>(A).\nonumber
$$

Таким образом, число \(A\) есть предел функции \(f(x)\) в точке \(a\), если для любой \(\varepsilon\)-окрестности числа \(A\) можно найти такую проколотую \(\delta\)-окрестность точки \(a\), что для всех \(x\), принадлежащих этой \(\delta\)-окрестности, соответствующие значения функции содержатся в \(\varepsilon\)-окрестности числа \(A\).

В определении предела функции в точке \(a\) предполагается, что \(x\neq a\). Это требование связано с тем, что точка \(a\) может не принадлежать области определения функции. Отсутствие этого требования сделало бы невозможным использование предела для определения производной, так как производная функции \(f(x)\) в точке \(a\) — это предел функции
$$
F(x) = \frac,\nonumber
$$
которая не определена в точке \(a\).

Отметим еще, что число \(\delta\), фигурирующее в определении предела, зависит, вообще говоря, от \(\varepsilon\), то есть \(\delta=\delta(\varepsilon)\).

Определение предела по Гейне.

Число \(A\) называется пределом функции \(f(x)\) в точке \(a\), если эта функция определена в некоторой проколотой окрестности точки \(\alpha\), то есть \(\exists\delta_<0>>0:\ \dot_<\delta_<0>>(a)\subset D(f)\), и для любой последовательности \(\\>\), сходящейся к \(a\) и такой, что \(x_\in U_<\delta_0>(a)\) для всех \(n\in\mathbb\), соответствующая последовательность значений функции \(\)\>\) сходится к числу \(A\).

Пользуясь определением предела по Гейне, доказать, что функция

$$
f(x)=\sin\frac<1>\nonumber
$$
не имеет предела в точке \(x=0\).

\(\triangle\) Достаточно показать, что существуют последовательности \(\\>\) и \(\<\widetilde_\>\) с отличными от нуля членами, сходящиеся к нулю и такие, что \(\displaystyle \lim_f(x_)\neq\lim_ f(\widetilde_n)\).

Тогда \(\displaystyle \lim_x_=\lim_\widetilde_=0,\ f(x_)=1\) и \(f(\widetilde_)=0\) для всех \(n\in\mathbb\) и поэтому \(\displaystyle \lim_f(x_)=1\), a \(\displaystyle \lim_f(\widetilde_)=0\). Следовательно, функция \(\displaystyle \sin\frac<1>\) не имеет предела в точке \(x=0.\quad \blacktriangle\)

Если функция \(f\) определена в проколотой \(\delta_<0>\)-окрестности точки \(a\) и существуют число \(A\) и последовательность \(\\) такие, что \(x_n \in \dot_<\delta_<0>>(a)\) при всех \(n \in\mathbb,\ \displaystyle \lim_x_=a\) и \(\displaystyle \lim_f(x_)=A\), то число \(A\) называют частичным пределом функции \(f\) в точке \(a\).

Так, например, для функции \(f(х)=\displaystyle \sin\frac<1>\) каждое число \(A \in [-1, 1]\) является ее частичным пределом. В самом деле, последовательность \(\\>\), где \(x_=\displaystyle (\arcsin A+2\pi n)^<-1>\), образованная из корней уравнения \(\displaystyle \sin\frac<1>=A\) (рис. 10.3), такова, что \(x_n\neq 0\) для всех \(n\in\mathbb,\ \displaystyle \lim_x_n=0\) и \(\displaystyle \lim_f(x_)=A\).

Рис. 10.3

Эквивалентность двух определений предела.

Определения предела функции по Коши и по Гейне эквиваленты.

\(\circ\) В определениях предела функции \(f(x)\) по Коши и по Гейне предполагается, что функция \(f\) определена в некоторой проколотой окрестности точки \(a\), то есть существует число \(\delta_0>0\) такое, что \(\dot_<\delta_<0>>\in D(f)\).

Пусть \(а\) — предельная точка числового множества \(E\), то есть такая точка, в любой окрестности которой содержится по крайней мере одна точка множества \(E\), отличная от \(a\). Тогда число \(A\) называют пределом по Коши функции \(f(x)\) в точке \(a\) по множеству \(E\) и обозначают \(\displaystyle \lim_f(x)=A\), если
$$
\forall\varepsilon>0\quad \exists\delta>0:\quad\forall x\in \dot_<\delta>(a)\cap E\rightarrow|f(x)-A|

Различные типы пределов.

Односторонние конечные пределы.

Число \(A\) называют пределом слева функции \(f(x)\) в точке a и обозначают \(\displaystyle \lim_>f(x)\) или \(f(a-0)\), если
$$
\forall\varepsilon>0\quad\exists\delta>0:\quad\forall x\in(a-\delta,a)\rightarrow|f(x)-A_<1>| 0\quad\exists\delta>0:\ \forall x\in (a,a+\delta)\rightarrow|f(x)-A_2| 0,
\end\right.\nonumber
$$
график которой изображен на рис. 10.4 \(\displaystyle \lim_f(x)=f(-0)=-1,\ \displaystyle \lim_f(x)=f(+0)=1\).

Рис. 10.4

Отметим еще, что если
$$
\forall\varepsilon>0\ \exists\delta>0:\forall x\in\dot_<\delta>(a)\rightarrow f(x)\in[A,A+\varepsilon),
$$
то есть значения функции лежат в правой \(\varepsilon\)-полуокрестности числа \(A\), то пишут \(\displaystyle \lim_f(x)=A+0\). В частности, если \(A=0\), то пишут \(\displaystyle \lim_f(x)=+0\).

Аналогично
$$
\displaystyle \<\lim_f(x)=A-0\>\Leftrightarrow\forall\varepsilon>0\ \exists\delta>0:\ \forall x\in\dot_<\delta>(a)\rightarrow f(x)\in (A-\varepsilon,A\rbrack.\nonumber
$$
Например, для функции
$$
\varphi (x)=\left\<\begin
1-x,\ если\ x 0,
\end\right.\nonumber
$$
график которой изображен на рис. 10.5, \(\displaystyle \lim_f(x)=1+0\).

Рис. 10.5

Аналогичный смысл имеют записи вида
$$
\lim_f(x)=A+0,\quad \lim_f(x)=A-0\nonumber
$$

Например,
$$
\displaystyle \<\lim_f(x)=A+0\>\Leftrightarrow\forall\varepsilon>0\exists\delta>0:\forall x\in(a-\delta,a)\rightarrow f(x)\in[A,A+\varepsilon).
$$

Бесконечные пределы в конечной точке.

Говорят, что функция \(f(x)\), определенная в некоторой проколотой окрестности точки \(a\), имеет в этой точке бесконечный предел, и пишут \(\lim_f(x)=\infty\), если
$$
\forall\varepsilon>0\quad\exists\delta>0:\ \forall x\in\dot_<\delta>(a)\rightarrow|f(x)|>\varepsilon.\label
$$

В этом случае функцию \(f(x)\) называют бесконечно большой при \(x\rightarrow a\).

Рис. 10.6

Например, если \(f(x)=1/x\), то \(\displaystyle \lim_f(x)=\infty\), так как условие \eqref выполняется при \(\delta=1/\varepsilon\) (рис.10.6).

Аналогично говорят, что функция \(f(x)\), определенная в некоторой проколотой окрестности точки \(a\), имеет в этой точке предел, равный \(+\infty\), и пишут \(\displaystyle \lim_f(x)=+\infty\), если \(\forall\varepsilon>0\quad\exists\delta>0:\ \forall x\in\dot_<\delta>(a)\rightarrow f(x)>\varepsilon\), то есть \(f(x)\in U_<\varepsilon>(+\infty)\), где множество \(U_\varepsilon (+\infty )\) называют \(\varepsilon\)-окрестностью символа \(+\infty\).

Если
$$
\forall\varepsilon>0\quad\exists\delta>0:\forall x\in\dot_<\delta>(a)\rightarrow f(x) Рис. 10.7 Рис. 10.8

Предел в бесконечности.

$$
\forall\varepsilon>0\exists\delta>0:\forall x\in U_<\delta>(+\infty)\rightarrow f(x)\in U_<\varepsilon>(A),\nonumber
$$

то говорят, что число \(A\) есть предел функции \(f(x)\) при x, стремящемся к плюс бесконечности, и пишут \(\displaystyle \lim_ f(x)=A.\)

Например, если \(f(x)=\displaystyle\frac<3-2x>\), то \(\displaystyle \lim_ f(x)=-2\). В самом деле \(f(x)=-2+\frac<5>\), и если \(x>0\), то \(x+1>x>0.\) Поэтому \(\displaystyle\frac<5> 0\) выполняется при любом \(x >\delta\), где \(\delta=\displaystyle\frac<5><\varepsilon>\), то есть при любом \(x\in U_<\delta>(+\infty)\).

Если \(\forall\varepsilon>0 \ \exists\delta>0:\forall x\in U_<\delta>(-\infty)\rightarrow f(x)\in U_<\varepsilon>(A)\), то есть неравенство \(|f(x)-A| 0\ \exists\delta>0:\forall x\in U_<\delta>(\infty)\rightarrow f(x)\in U_<\varepsilon>(A),\nonumber
$$
то говорят, что число A есть предел функции f(x) при x, стремящемся к бесконечности, и пишут \(\displaystyle \lim_=A\). Например, если \(f(x)=\frac<3-2x>\), то \(\displaystyle \lim_f(x)=-2.\)

Точно так же вводится понятие бесконечного предела в бесконечности. Например,запись \(\displaystyle \lim_ f(x)=-\infty\) означает, что
$$
\forall\varepsilon>0\ \exists\delta>0:\forall x\in U_<\delta>(+\infty)\rightarrow f(x)\in U_<\varepsilon>(-\infty).\nonumber
$$
Аналогично определяются бесконечные пределы при \(x\rightarrow\infty\) и \(x\rightarrow-\infty.\)

Свойства пределов функций.

Локальные свойства функции, имеющей предел.

Покажем, что функция, имеющая конечный предел в заданной точке, обладает некоторыми локальными свойствами, то есть свойствами, которые справедливы в окрестности этой точки.

Если функция \(f(x)\) имеет предел в точке \(a\), то существует такая проколотая окрестность точки \(a\), в которой эта функция ограничена.

\(\circ\) Пусть \(\displaystyle \lim_f(x)=A\). В силу определения предела по заданному числу \(\varepsilon=1\) можно найти число \(\delta>0\) такое, что для всех \(x\in\dot_<\delta>(a)\) выполняется неравенство \(|f(x)-A| Свойство 2

Свойство сохранения знака предела.

Если \(\displaystyle \lim_f(x)=A\), причем \(A\neq 0,\) то найдется такая проколотая окрестность точки \(a\), в которой значения функции \(f\) имеют тот же знак, что и число \(A\).

\(\circ\) Согласно определению предела по заданному числу \(\varepsilon = \frac<|A|><2>>0\) можно найти такое число \(\delta>0\), что для всех \(x\in\dot_<\delta>(a)\) выполняется неравенство \(\displaystyle |f(x)-A| 0\), то из левого неравенства \eqref следует, что
$$
f(x)>\frac<2>>0\ для\ x\in\dot_<\delta>(a).\nonumber
$$
Если \(A Свойство 3

Если \(\displaystyle \lim_g(x)=B\), причем \( B\neq0\), то существует число \(\delta>0\) такое, что функция \(\displaystyle\frac<1>\) ограничена на множестве \(\dot_<\delta>(a).\)

\(\circ\) В силу определения предела по заданному числу \(\varepsilon=\frac<|B|><2>\) можно найти число \(\delta>0\), такое, что для всех \(x\in\dot_\delta(a)\) выполняется неравенство
$$
|g(x)-B| \frac<|B|><2>\),и поэтому \(\displaystyle \frac<1> <|g(x)|>Свойство 1

Если существует число \(\delta>0\) такое, что для всех \(\dot_<\delta>(a)\) выполняются неравенства
$$
g(x)\leq f(x)\leq h(x),\label
$$
и если
$$
\lim_g(x)=\lim_h(x)=A,\label
$$
то существует \(\displaystyle \lim_f(x)=A.\)

\(\circ\) Воспользуемся определением предела функции по Гейне. Пусть \(\\>\) — произвольная последовательность такая, что \(x_n\in\dot_<\delta>(a)\) для \(n\in\mathbb\) и \(\displaystyle \lim_f(x)=a\). Тогда в силу условия \eqref \(\displaystyle \lim_g(x_)=\lim_h(x_)=A.\)

Так как, согласно условию \eqref, для всех \(n\in\mathbb\) выполняется неравенство
$$
g(x_)\leq f(x_)\leq h(x_),\nonumber
$$
то в силу свойств пределов последовательностей \(\displaystyle \lim_f(x_)=A\). Следовательно, \(\displaystyle \lim_f(x)=A.\ \bullet\)

\(\circ\) Для доказательства этого свойства достаточно воспользоваться определением предела функции по Гейне и соответствующими свойствами пределов последовательностей. \(\bullet\)

Бесконечно малые функции обладают следующими свойствами:

Эти свойства легко доказать, используя определения бесконечно малой и ограниченной функции, либо с помощью определения предела функции по Гейне и свойств бесконечно малых последовательностей. Из свойства 2) следует, что произведение конечного числа бесконечно малых при \(x\rightarrow a\) функций есть бесконечно малая при \(x\rightarrow a\) функция.

Из определения предела функции и определения бесконечно малой функции следует, что число \(A\) является пределом функции \(f(x)\) в точке \(a\) тогда и только тогда, когда эта функция представляется в виде
$$
f(x)=A+a(x),\nonumber
$$ где \(a(x)\) — бесконечно малая при \(x\rightarrow a\) функция.

Свойства пределов, связанные с арифметическими операциями.

Если функции \(f(x)\) и \(g(x)\) имеют конечные пределы в точке \(а\), причем \(\displaystyle \lim_f(x)=A,\ \lim_g(x)=B\), то:

\(\circ\) Для доказательства этих свойств достаточно воспользоваться определением предела функции по Гейне и свойствами пределов последовательностей. \(\bullet\)

Отметим частный случай утверждения \eqref:
$$
\lim_(C f(x))=C\lim_f(x),\nonumber
$$
то есть постоянный множитель можно вынести за знак предела.

Пределы монотонных функций.

Ранее мы уже ввели понятие монотонной функции. Докажем теорему о существовании односторонних пределов у монотонной функции.

Если функция \(f\) определена и является монотонной на отрезке \([a,b]\), то в каждой точке \(x_<0>\in(a,b)\) эта функция имеет конечные пределы слева и справа, a в точках \(а\) и \(b\) — соответственно правый и левый пределы.

\(\circ\) Пусть, например, функция \(f\) является возрастающей на отрезке \([a,b]\). Зафиксируем точку \(х_0\in\)(а, \(b\)]. Тогда
$$
\forall x\in[a,x_<0>)\rightarrow f(x)\leq f(x_<0>).\label
$$

В силу условия \eqref множество значений, которые функция \(f\) принимает на промежутке \([a,x_<0>)\), ограничено сверху, и по теореме о точной верхней грани существует
$$
\sup_\in[a,\ x_<0>):M-\varepsilon 0\), так как \(x_\varepsilon 0\ \exists\delta>0:\forall x\in(x_<0>-\delta,x_<0>)\rightarrow f(x)\in(M-\varepsilon,M].\nonumber
$$
Согласно определению предела слева это означает, что существует
$$
\lim_-0> f(x)=f(x_<0>-0)=M.\nonumber
$$
Итак,
$$
f(x_<0>-0)=\sup_

Если функция \(f\) определена и возрастает на отрезке \([a,b],\ x_<0>\in(a,b),\) то
$$
f(x_<0>-0) Замечание.

Теорема о пределе монотонной функции справедлива для любого конечного или бесконечного промежутка. При этом, если \(f\) — возрастающая функция, не ограниченная сверху на \((a,b)\), то \(\displaystyle \lim_f(x)= +\infty\) (в случае, когда \(b =+\infty\) пишут \(\displaystyle \lim_f(x)= +\infty\)), а если \(f\) — возрастающая и не ограниченная снизу на промежутке \((a,b)\) функция, то \(\displaystyle \lim_f(x)=-\infty\quad (\lim_f(x)=-\infty)\).

Критерий Коши существования предела функции.

Будем говорить, что функция \(f(x)\) удовлетворяет в точке \(x=a\) условию Коши, если она определена в некоторой проколотой окрестности точки \(a\) и
$$
\forall\varepsilon>0\quad \exists\delta=\delta(\varepsilon)>0:\ \forall x’,x″\in \dot_<\delta>(a)\rightarrow|f(x’)-f(x″)|

Пусть существует число \(\delta >0\) такое, что функция \(f(x)\) определена в проколотой \(\delta\) — окрестности точки \(a\), и пусть для каждой последовательности <\(x_n\)>, удовлетворяющей условию \(x_n\in\dot_<\delta>(a)\) при всех \(n\in\mathbb\) и сходящейся к \(a\), соответствующая последовательность значений функции \(\) имеет конечный предел. Тогда этот предел не зависит от выбора последовательности \(\), то есть если
$$
\lim_f(x_)=A,\nonumber
$$
и
$$
\lim_f(\widetilde>)=\widetilde,\nonumber
$$
где \(\widetilde_n =\dot_<\delta>(a)\) при всех \(n \in\mathbb\) и \( \widetilde_\rightarrow a \) при \(n\rightarrow\infty\) то \(\widetilde=A.\)

\(\circ\) Образуем последовательность
$$
x_<1>,\widetilde_<1>, x_<2>,\widetilde_<2>,\ldots, x_,\widetilde_,\ldots\nonumber
$$
и обозначим k-й член этой последовательности через \(y_\). Так как \(\displaystyle \lim_y_k=a\) (см. пример 3 здесь) и \(y_k\in \dot_<\delta>(a)\) при любом \(k\in\mathbb\), то по условию леммы существует конечный \(\displaystyle \lim_f(y_)=A’\) Заметим, что \(\)\>\) и \(\_)\>\) являются подпоследовательностями сходящейся последовательности \(\\). Поэтому \(A=A’,\widetilde=A’\) откуда получаем, что \(A=\widetilde.\ \bullet\)

Для того чтобы существовал конечный предел функции \(f(x)\) в точке \(x = a\) необходимо и достаточно, чтобы эта функция удовлетворяла в точке a условию Коши \eqref.

\(\circ\) Необходимость. Пусть \(\displaystyle \lim_f(x)=A\); тогда
$$
\forall\varepsilon>0 \ \exists\delta>0:\forall x\in\dot_<\delta>(a)\rightarrow|f(x)-A| 0\) можно найти число \(\delta=\delta_\varepsilon>0\) такое, что
$$
\forall x’,x″\in \dot_<\delta>(a)\rightarrow|f(x’)-f(x″)| 0,\) указанное в условии \eqref, найдем в силу определения предела последовательности номер \(n_<\delta>=N_<\varepsilon>\) такой, что
$$
\forall n>N_<\varepsilon>\rightarrow 0 Замечание.

Теорема 3 остается в силе, если точку \(a\) заменить одним из символов \(a-0, a+0,-\infty, +\infty\); при этом условие \eqref должно выполняться в окрестности этого символа.

Источник

Доказать с помощью определения предела функции

Доброго времени суток!

Доказать через определение предела, подробнее, пожалуйста, т.к. не понимаю, что делать нужно.

задан 19 Ноя ’13 12:40

Нужно доказать, а не решить, вот в чем проблема, с помощью, как я поняла определения Коши.

Слово «доказать» означает вывести из известных положений: аксиом, опредлений, лемм, теорем. Все перечисленные утверждения выводятся из теорем о пределах. Если же этими теоремами пользоваться не разрешено, то в условии задачи такая вещь должна быть явно оговорена. Рассуждения при этом становятся несколько более сложными, но возможно доказательство, опирающееся только на определение предела и на элементарные свойства неравенств. Если нужно, я по каждому пункту могу продемонстрировать, как это делается.

1 ответ

отвечен 19 Ноя ’13 15:46

falcao
242k ● 1 ● 34 ● 48

Если вас не затруднит, то напишите, пожалуйста, как это же доказательство нужно сделать, но для лимита равного не конкретному числу, как в этом примере числу 2, а бесконечности. А будет ещё лучше, если для оставшихся двух моих примеров, чтоб уж наверняка понимать как и что делать. Заранее спасибо 🙂

Первое определение предела функции (по Гейне)

Здесь x и a могут быть как конечными числами, так и бесконечно удаленными точками. Окрестность может быть как двусторонней, так и односторонней.

Запишем это определение с помощью логических символов существования и всеобщности:
.

Второе определение предела функции (по Коши)

Точки x и a могут быть как конечными числами, так и бесконечно удаленными точками. Окрестность также может быть как двусторонней, так и односторонней.

Запишем это определение с помощью логических символов существования и всеобщности:
.

В этом определении используются окрестности с равноудаленными концами. Можно дать и эквивалентное определение, используя произвольные окрестности точек.

С помощью логических символов существования и всеобщности это определение можно записать так:
.

На странице «Окрестность точки» мы показали, что определение предела функции с использованием более простой окрестности с равноудаленными концами эквивалентно определению, в котором используется произвольная окрестность. Формулировка второго определения по Коши имеет более общий вид, и оно часто используется при доказательстве теорем. Первое определение, в математическом смысле, проще. Его удобно применять в вычислениях.

Более подробно определение Коши для конечных точек рассматривается на странице «Определение предела функции в конечной точке»; для бесконечно удаленных точек – на странице «Определение предела функции на бесконечности».

Односторонние и двусторонние пределы

Для определения предела по Коши нужно в каждом случае преобразовать выражения и в неравенства, используя соответствующие определения окрестности точки.
См. «Окрестность точки».

Определение, что точка a не является пределом функции

Эквивалентность определений предела по Гейне и по Коши

Теорема
Определения предела функции по Гейне и по Коши эквивалентны.

При доказательстве мы предполагаем, что функция определена в некоторой проколотой окрестности точки (конечной или бесконечно удаленной). Точка a также может быть конечной или бесконечно удаленной.

Доказательство Гейне ⇒ Коши

Первая часть доказана.

Доказательство Коши ⇒ Гейне

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

Решение

Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными ­ – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

Докажите, что существует конечный предел функции f ( x ) = 1 6 ( x – 8 ) 2 – 8 в точке x 0 = 2 и вычислите его значение.

Решение

Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник