Изометрия что это такое определение

Изометрическая проекция

Изометри́ческая прое́кция — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроектированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так.

Изометрическая проекция используется в машиностроительном черчении и САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для трёхмерных объектов и панорам.

Содержание

Стандартные изометрические проекции [1]

Прямоугольная (ортогональная) изометрическая проекция

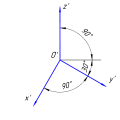
В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z’ направлена вертикально. Коэффициенты искажения () имеют числовое значение . Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в раза.

Косоугольная фронтальная изометрическая проекция

Ось Z’ направлена вертикально, угол между осью X’ и Z’ равен 90°, ось Y’ с углом наклона 135° (допускается 120° и 150°) от оси Z’.

Фронтальная изометрическая проекция выполняется по осям X’, Y’ и Z’ без искажения.

Кривые параллельные фронтальной плоскости проецируются без искажений.

Косоугольная горизонтальная изометрическая проекция

Ось Z’ направлена вертикально, между осью Z’ и осью Y’ угол наклона равен 120° (допускается 135° и 150°), при этом сохраняется угол между осями X’ и Y’ равным 90°.

Горизонтальную изометрическую проекцию выполняют без искажения по осям X’, Y’ и Z’.

Кривые, параллельные горизонтальной плоскости [2] проецируются без искажений.

Визуализация

Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. К примеру, если взять куб, это можно выполнить направив взгляд на одну из граней куба, после чего повернув куб на ±45° вокруг вертикальной оси и на ±arcsin (tan 30°) ≈ 35.264° вокруг горизонтальной оси. Обратите внимание: на иллюстрации изометрической проекции куба контур проекции образует правильный шестиугольник — все рёбра равной длины и все грани равной площади.

Подобным же образом изометрический вид может быть получен, к примеру, в редакторе трёхмерных сцен: начав с камерой, выровненной параллельно полу и координатным осям, её нужно повернуть вниз на ≈35.264° вокруг горизонтальной оси и на ±45° вокруг вертикальной оси.

Другой путь визуализации изометрической проекции заключается в рассмотрении вида кубической комнаты с верхнего угла с направлением взгляда в противолежащий нижний угол. Ось x здесь направлена диагонально вниз и вправо, ось y — диагонально вниз и влево, ось z — прямо вверх. Глубина также отражается высотой картинки. Линии, нарисованные вдоль осей, имеют угол 120° между собой.

Матричные преобразования

Имеется 8 различных вариантов получения изометрической проекции в зависимости от того, в какой октант смотрит наблюдатель. Изометрическое преобразование точки в трёхмерном пространстве в точку на плоскости при взгляде в первый октант может быть математически описано с помощью матриц поворота следующим образом. Вначале, как объяснено в разделе Визуализация, выполняется поворот вокруг горизонтальной оси (здесь x) на α = arcsin (tan 30°) ≈ 35.264° и вокруг вертикальной оси (здесь y) на β = 45°:

Затем применяется ортогональная проекция на плоскость x-y:

Другие семь возможных видов получаются поворотом к противостоящим сторонам и/или инверсией направления взгляда. [3]

Ограничения аксонометрической проекции

Как и в других видах параллельных проекций, объекты в аксонометрической проекции не выглядят больше или меньше при приближении или удалении от наблюдателя. Это полезно в архитектурных чертежах и удобно в спрайто-ориентированных компьютерных играх, но, в отличие от перспективной (центральной) проекции, приводит к ощущению искривления, поскольку наши глаза или фотография работают иначе.

Это также легко приводит к ситуациям, когда глубину и высоту невозможно оценить, как показано на иллюстрации справа. В этом изометрическом рисунке голубой шар на два уровня выше красного, но это нельзя увидеть, если смотреть только на левую половину картинки. Если выступ, на котором находится голубой шар, расширить на один квадрат, то он окажется точно рядом с квадратом, на котором находится красный шар, создавая оптическую иллюзию, будто оба шара на одном уровне.

Дополнительная проблема, специфичная для изометрической проекции — сложность определения, какая сторона объекта наблюдается. При отсутствии теней и для объектов, которые относительно перпендикулярны и соразмерны, сложно определить, какая сторона является верхней, нижней или боковой. Это происходит из-за приблизительно равных по размеру и площади проекций такого объекта.

Большинство современных компьютерных игр избегают этого за счёт отказа от аксонометрической проекции в пользу перспективного трёхмерного рендеринга. Однако эксплуатация проекционных иллюзий популярна в оптическом искусстве — таком, как работы из серии «невозможной архитектуры» Эшера. Водопад (1961) — хороший пример, в котором строение в основном изометрическое, в то время как блеклый фон использует перспективную проекцию. Другое преимущество заключается в том, что в черчении даже новички легко могут строить углы в 60° с помощью только циркуля и линейки.

Изометрическая проекция в компьютерных играх и пиксельной графике

В области компьютерных игр и пиксельной графики аксонометрическая проекция была весьма популярна в силу лёгкости, с которой двухмерные спрайты и плиточная графика (англ.) могли быть использованы для представления трёхмерной игровой среды — поскольку во время перемещения по игровому полю объекты не меняют размер, компьютеру не требуется масштабировать спрайты или выполнять вычисления, необходимые для моделирования визуальной перспективы. Это позволяло старым 8-битным и 16-битным игровым системам (и, позднее, портативным игровым системам) легко отображать большие трёхмерные пространства. И хотя неразбериха с глубиной (см. выше) иногда могла быть проблемой, хороший дизайн игры способен её смягчить. С приходом более мощных графических систем аксонометрическая проекция стала терять свои позиции.

Проекция в компьютерных играх обычно несколько отличается от «истинной» изометрической в силу ограничений растровой графики — линии по осям x и y не имели бы аккуратного пиксельного узора, если бы рисовались под углом в 30° к горизонтали. Хотя современные компьютеры могут устранять эту проблему с помощью сглаживания, ранее компьютерная графика не поддерживала достаточную цветовую палитру или не располагала достаточной мощностью процессоров для его выполнения. Вместо этого использовалась пропорция пиксельного узора 2:1 для рисования осевых линий x и y, в результате чего эти оси располагались под углом arctan 0,5 ≈ 26,565° к горизонтали. (Игровые системы с неквадратными пикселями могли, однако, приводить к другим углам, включая полностью изометрические). Поскольку здесь из трёх углов между осями (116,565°, 116,565°, 126,87°) равны только два, такой вид проекции более точно характеризуется как вариация диметрической проекции. Однако большинство представителей сообществ компьютерных игр и растровой графики продолжает называть эту проекцию «изометрической перспективой». Также, часто используются термины «вид 3/4 (англ.)» и «2.5D».

История изометрических компьютерных игр

На протяжении 1990-х некоторые очень успешные игры вроде Civilization II и Diablo использовали фиксированную изометрическую перспективу. С приходом 3D ускорителей на персональные компьютеры и игровые консоли игры с трёхмерной перспективой в основном переключились на полноценную трёхмерность вместо изометрической перспективы. Это можно видеть в преемницах вышеназванных игр — начиная с Civilization IV в этой серии используется полная трёхмерность. Diablo II, как и ранее, использует фиксированную перспективу, но опционально применяет перспективное масштабирование спрайтов на расстоянии, получая псевдо-трёхмерную перспективу. [18]

Источник

Изометрия

См. также

Список значений слова или словосочетания со ссылками на соответствующие статьи. Если вы попали сюда из другой статьи Википедии, пожалуйста, вернитесь и уточните ссылку так, чтобы она указывала на статью.

Смотреть что такое «Изометрия» в других словарях:

изометрия — изометрия … Орфографический словарь-справочник

ИЗОМЕТРИЯ — (греч.). Деление на равные части, доли. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ИЗОМЕТРИЯ греч., от isos, одинаковый, равный, и metreo, меряю. Измерение равными частями. Объяснение 25000 иностранных слов,… … Словарь иностранных слов русского языка

изометрия — изометрическое представление Изображение, в котором все три измерения объекта отображаются в одинаковой пропорции. Изометрическое представление не показывает перспективу. [http://www.morepc.ru/dict/] Тематики информационные технологии в целом… … Справочник технического переводчика

Изометрия — см. Аксонометрия … Издательский словарь-справочник

ИЗОМЕТРИЯ — вид (см.) с одинаковым коэффициентом искажения по трём осям проекций, расположенным под углом 120° друг к другу … Большая политехническая энциклопедия

ИЗОМЕТРИЯ — см. в ст. Аксонометрия … Большой энциклопедический политехнический словарь

изометрия — изом етр ия, и … Русский орфографический словарь

ИЗОМЕТРИЯ — сохранение пропорций органов и частей тела в период роста организма … Словарь ботанических терминов

изометрия — (1 ж), Р., Д., Пр. изоме/три/и … Орфографический словарь русского языка

Источник

Понятие об аксонометрических проекциях

Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.

Одним из видов наглядных изображений являются аксонометрические изображения.

Аксонометрия в переводе с греческого означает «измерение по осям».

Аксонометрические проекции получают путём проецирования параллельными лучами

предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).

Таким образом, аксонометрическая проекция – это проекция только на одну плоскость.

Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.

Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.

Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.

Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.

В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).

Стандартные виды аксонометрии. Изометрия. Диметрия

Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.

Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.

Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.

Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.

На рис. 104б и в приведены два способа построения осей в изометрии.

Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.

Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у – угол 41°25′.

Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.

В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у – 0,47. При построениях первый коэффициент округляют до 1, а второй – до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.

Построение окружности в аксонометрии

Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).

Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр – диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.

Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.

Наиболее простой способ построения овала показан на рис. 107.

На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.

Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой – 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.

Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.

На рис. 110б строим оси диметрии х_р, у_р, z_р. Затем строим прямую, перпендикулярную оси у_р. Отложив на осях х_р и z_р радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала. Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью у_р и перпендикуляром к ней получим точки О₁, О₂, О₃, О₄. Из центров O₁ и О₃ опишем дуги радиусом R₁=О₃ K, а из центров О₂ и О₄ – дуги радиусом R₂=О₂M.

Аксонометрические изображения предметов

Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.

Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.

На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.

На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.

Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).

рис. 111 рис. 112 рис. 113

Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).

Источник

Изометрия в играх. С чего все начиналось?

Привет друзья! Я думаю, что нет такого человека, который бы не сталкивался с играми в изометрии, будь то это какая-то ролевая игра, стратегия или вообще любой другой жанр. И сегодня мы обсудим именно эту тему – тему изометрической проекции в видеоиграх.

В данном блоге мы, вспомним первые игры в изометрии, поговорим для чего она нужна, как развивалась, и попытаемся понять, почему использование этой проекции всё чаще применяется в игровой индустрии и почему она нравятся игрокам?

Если хочешь усвоить всю эту информацию в простой и расслабляющей форме, то можешь пройти по ссылке на видео!

Сложилось так, что изометрия в видеоиграх используется по разным причинам. Вот, например, первые подобные проекты использовали изометрию для имитации в 2D играх ЗD графики, недоступной для компьютеров и приставок того времени. Когда же такая возможность представилась, разработчики продолжили использовать изометрию отчасти из-за трудностей изучения новых технологий, отчасти из-за финансовой составляющей, ведь 3D графика была дорогим удовольствием. В нынешнее время изометрия неотъемлема для некоторых игр, так как привязана к серии, например, Diablo никто не может представить её не в изометрии или к жанру, например, стратегии. Некоторые игры просто используют изометрию как отличительную особенность.

Ну а вообще, что такое изометрия?

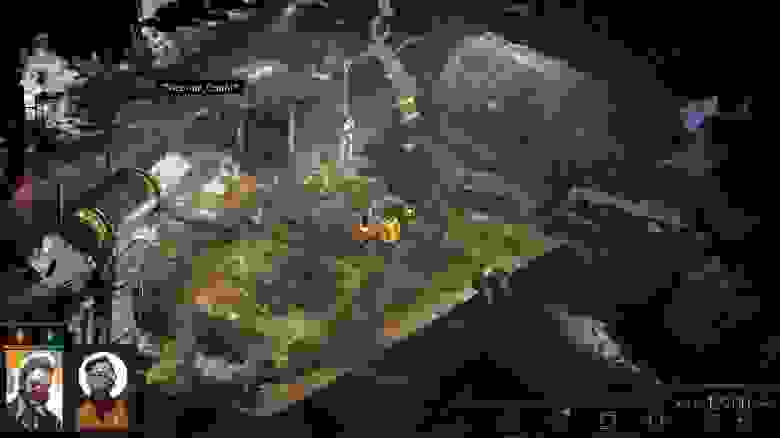
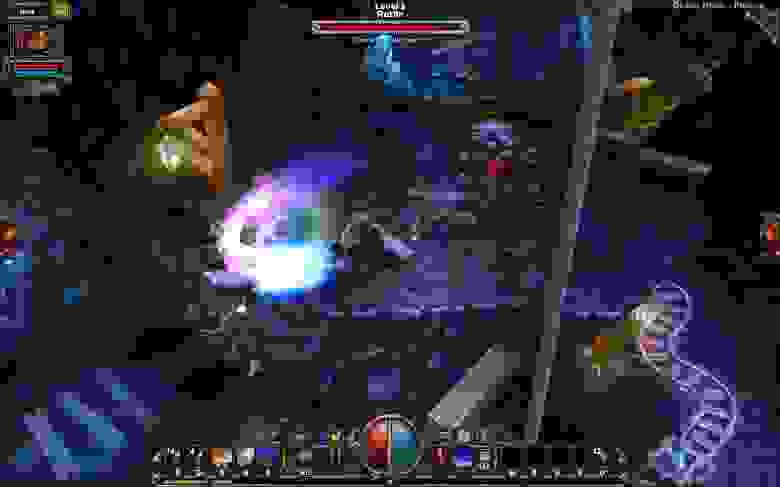
Само понятие изометрии в компьютерных играх относится к тому или иному виду параллельной проекции с особым расположением камеры. Где угол обзора смещён так что позволяет создаёт эффект трёхмерности и позволяет показать некоторые детали окружения, которые не видны при виде сверху или виде сбоку. Вот вам несколько примеров изометрии в деле: XCOM 2, Diablo III и Disco Elysium.

Но несмотря на название, изометрическая компьютерная графика не обязательно является истинно изометрической – т.е. оси не всегда ориентированы под углом 120° друг к другу. Вот вам наглядный пример, истинный изометрический рисунок куба (сверху), можете обратить здесь внимание на углы и равную длину каждого из ребер куба, соотношение пикселей в такой изометрии будет примерно 1,732:1, а вот диметрическая проекция (снизу) которая в основном и используется в играх, тут уже и разные углы, и только некоторые ребра равны, но соотношение сторон уже 2:1.

Соотношение углов в Истинной Изометрии, можем увидеть, что углы по 120°, как и говорилось ранее

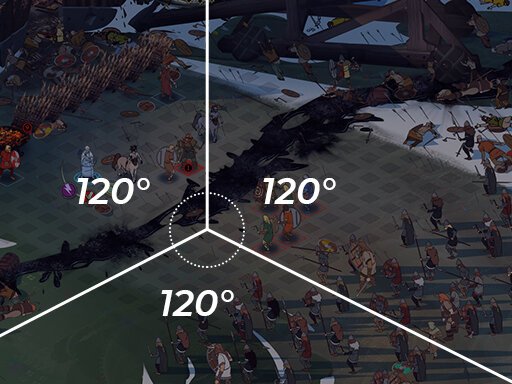
Проекция, используемая в видеоиграх, немного отличается от «истинной» изометрии из-за ограничений растровой графики. Линии в направлениях X и Y не будут следовать аккуратному пиксельному узору, если они нарисованы под нужным углом 30° к горизонтали.

Пример нарисованной пиксельной линии под углом 30° и пример того как новые компьютеры справлялись с проблемой благодаря сглаживанию

В то время как современные компьютеры могут устранить эту проблему с помощью сглаживания, более ранняя компьютерная графика не поддерживала достаточное количество цветов или не обладала достаточной мощностью процессора для этого. Поэтому для рисования осей X и Y использовали соотношение 2:1, т.е. диметрическую проекцию.

Соотношение углов в Диметрической проекции

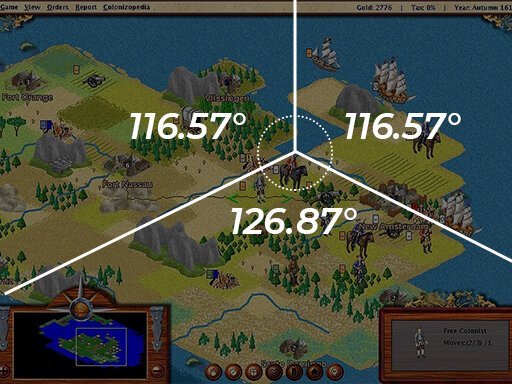
А на слайдах ниже вы можете увидеть соответствующие углы поворота 3D-камеры для истинной изометрической проекции (сверху) и для диметрической проекции (снизу). И из всего этого мы можем сделать вывод, что раньше и не было истинной изометрии, так как ее было трудно воплотить.

Но изометрическая и диметрическая проекция — это не все, на самом деле в играх используются различные виды проекции схожие с изометрией, например:

Использующие триметрическую проекцию, такие игры как первый Fallout и SimCity 4

Соотношение углов в Триметрической проекции

Использующие косоугольную проекцию, Ultima Online

Комбинация перспективной проекции и вида с высоты птичьего полёта, например, Torchlight и Divinity: Original Sin

Разные виды проекции

Но в итоге свелось к одному мы просто привыкли называть все это кратко, ИЗОМЕТРИЯ!

Изометрия в играх

В области видеоигр метод изометрической проекции стал популярным из-за лёгкости, с которой можно сделать 2D графику на основе спрайтов и плиток для представления трёхмерной игровой среды. Поскольку параллельно проецируемые объекты не изменяются в размере при перемещении по области, компьютеру нет необходимости масштабировать спрайты или выполнять сложные вычисления, необходимые для имитации визуальной перспективы.

Из плюсов изометрии мы можем отметить то, что использование изометрической или почти изометрической перспективы в видеоиграх даёт преимущества игрового процесса. Например, по сравнению с top-down игрой где проекция строго сверху, они добавляют третье измерение, которое открывает новые возможности для игрока.

Так же, по сравнению с видеоиграми от первого или третьего лица, они позволяют вам легче управлять большим количеством юнитов, например, целой группой персонажей в какой-нибудь РПГ или большой армией в стратегии. Поэтому стратегии и ролевых игр с механикой управления группой персонажей так сильно подружились с изометрией.

Кроме того, изометрия может облегчить ситуации, когда игрок может отвлекаться от основной механики игры из-за необходимости постоянно управлять громоздкой 3D-камерой. То есть, игрок может сосредоточиться на самой игре, а не на манипулировании игровой камерой во время активных действий.

На слайде можем увидеть, что изометрия показывает большую информации игроку, например врагов сзади. Во время активных действий мы можем наблюдать все поле боя, и нам не приходится крутить камерой в разные стороны.

Останемся мы конечно не без недостатков, одним из главных недостатков в изометрической графике является то, что по мере того, как разрешения и соотношения сторон дисплея продолжают развиваться, статические 2D изображения необходимо каждый раз повторно визуализировать, чтобы идти в ногу со временем, и не страдать от эффектов пикселизации и использовать – anti-aliasing или на русском технология сглаживания.

Однако повторный рендеринг игровой графики не всегда возможен. Например, как это было в 2012 году, когда студия Beamdog переделывала Baldur’s Gate от BioWare 1998 года, то студии не хватало оригинальных ресурсов разработчиков из-за того, что исходные данные были потеряны в результате наводнения, и они выбрали простое масштабирование 2D графики со сглаживанием без повторного рендеринга игровых спрайтов. Результатом была игра с определённой нечёткостью или её отсутствием по сравнению с графикой оригинальной игры.

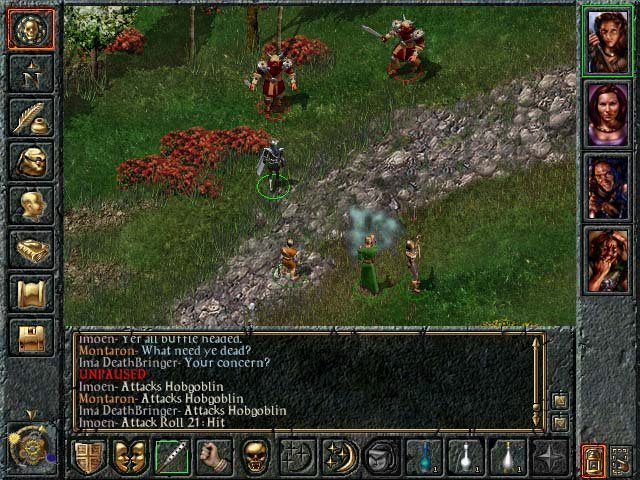
Сверху Baldur’s Gate 98 года, снизу Baldur’s Gate: Enhanced Editio (можно заметить небольшое замыливание и некоторую нечеткость).

Ну с теорией закончили прейдём к играм.

В то время как настоящие 3D в играх можно было увидеть уже в начале 70-х годов, первыми же видеоиграми, в которых использовался особый визуальный стиль изометрической проекции были аркадные игры в начале 80-х годов.

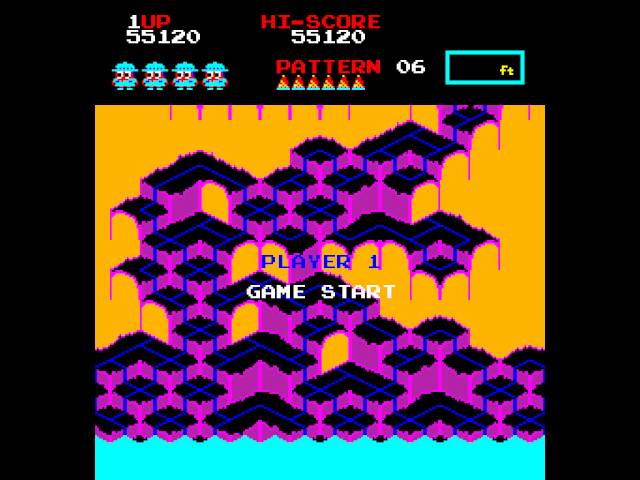
Как принято считать начало изометрии положила Игра Zaxxon от Sega вышедшая в апреле 1982 года, но скажу вам, что это было не совсем так. Первой же игрой в изометрии стала Treasure Island которая вышла в сентябре 1981 года под предводительством Японской компании Data East Corporation ну или DECO загвоздка в том, что она была выпущена в 1981 только для Японии, а на международный рынок вышла в июне 1982.

Изображение игры Treasure Island

В свою очередь Zaxxon, была выпущенная на международном уровне в апреле 1982 года, но в Японии она был выпущен в декабре 1981 года, она была значительно популярнее и более влиятельнее. После выпуска игра имела коммерческий успех и вошла в пятёрку самых прибыльных аркадных игр того года. Поэтому ее и считают первой изометрической игрой.

Изображение игры Zaxxon

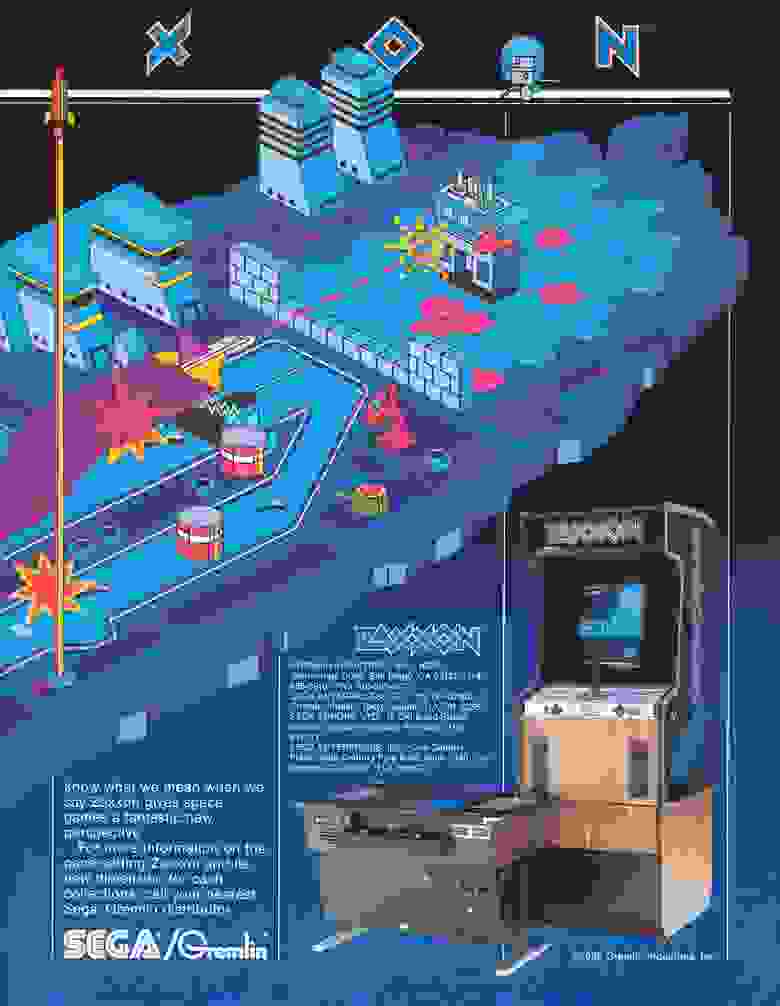
И да вот вам интересный факт Название игры Zaxxon происходит от другого названия изометрии, axonometric projection, (AXXON from AXONometric projection) или аксонометрическая проекция это считайте синонимы.

Изображение игры Q*bert

В следующем году в феврале 83 года была выпущена изометрическая платформер-аркада Congo Bongo, работала на том же оборудовании, что и Zaxxon. Это позволяет персонажу игрока перемещаться по большим изометрическим уровням, включая истинное трёхмерное лазание и падение.

Изображение игры Congo Bongo

Вскоре в 1983 году изометрические игры перестали быть эксклюзивными для аркадного рынка, и пришли в домашние компьютеры с выпуском Blue Max для 8-битного семейства Atari и Ant Attack для ZX Spectrum. В Ant Attack игрок мог двигаться вперед в любом направлении прокрутки, игра, предлагая полное свободное движение, а не фиксированное на одной оси, как в Zaxxon. Виды также можно было изменять вокруг 90° оси.

Blue Max для Atari

Ant Attack для ZX Spectrum

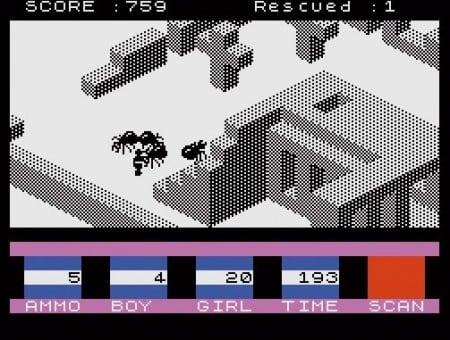
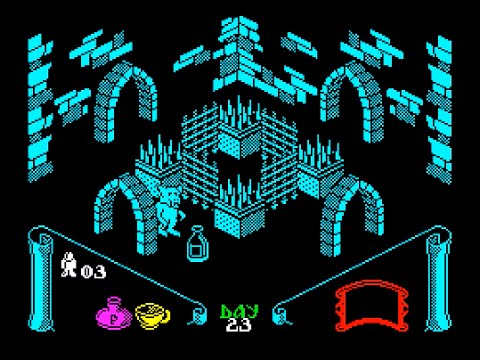
Годом позже на ZX Spectrum была выпущена игра Knight Lore, которая обычно считается революционным проектом, которая определила жанр изометрических игр на годы вперёд, однако изометрия не ограничивалась аркадными-приключенческими играми, так же в середине 80-х начали активно выходить и стратегии.

Изображение игры Knight Lore

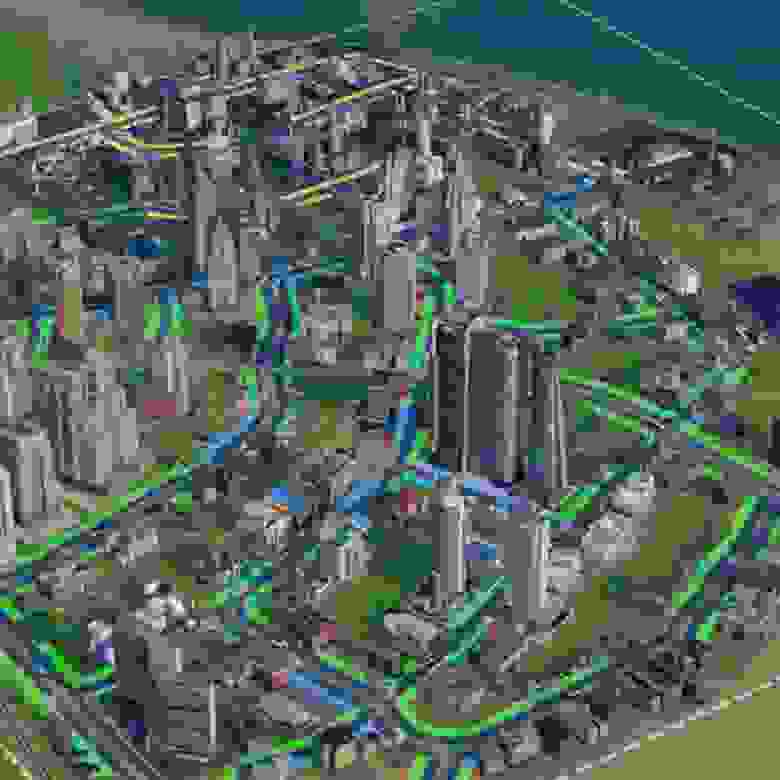
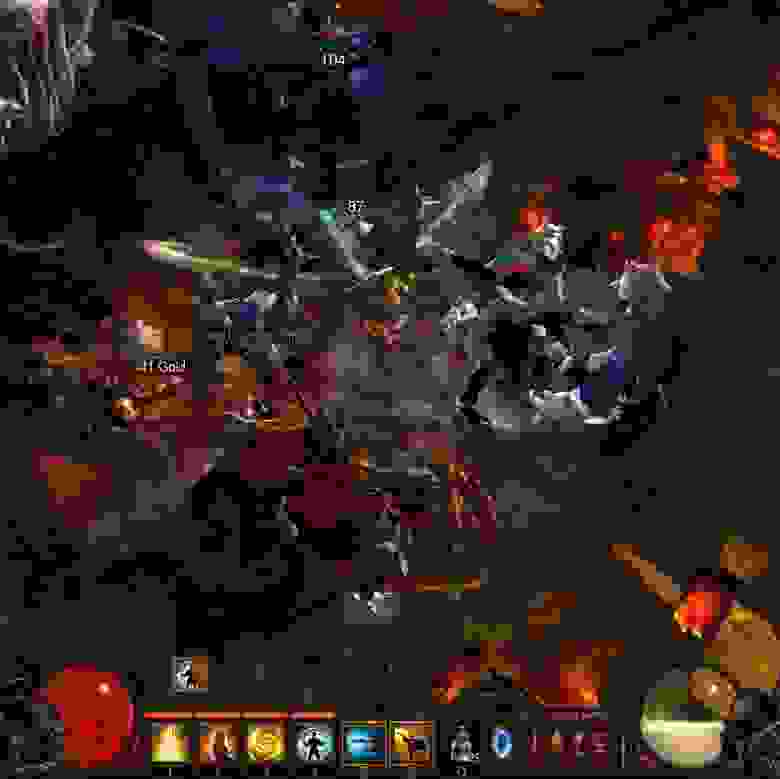
Дальше на протяжении 90х годов появлялись успешные и знаменитые изометрические проекты, которые известны и по сей день, такие как SimCity 2000 (1994), Civilization II (1996), X-COM (1994) и Diablo (1996), и везде использовалась фиксированная изометрическая перспектива. Но с появлением уже 3D-ускорения на персональных компьютерах и игровых консолях игры, ранее использовавшие 2D-перспективу, как правило, вместо этого начали переключаться на истинное 3D и изометрию.

Это можно увидеть в преемниках вышеупомянутых игр: например, SimCity, Civilization VI, XCOM 2 и Diablo III. Они уже используют трёхмерную полигональную графику. Потом время изометрии начало немного утихать.

SimCity. Как было и как стало

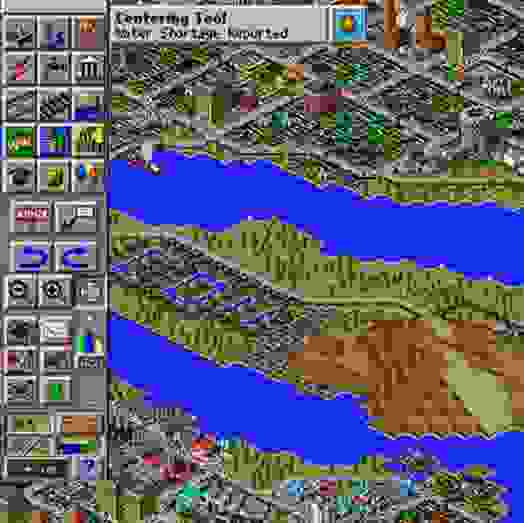
Civilization. Как было и как стало

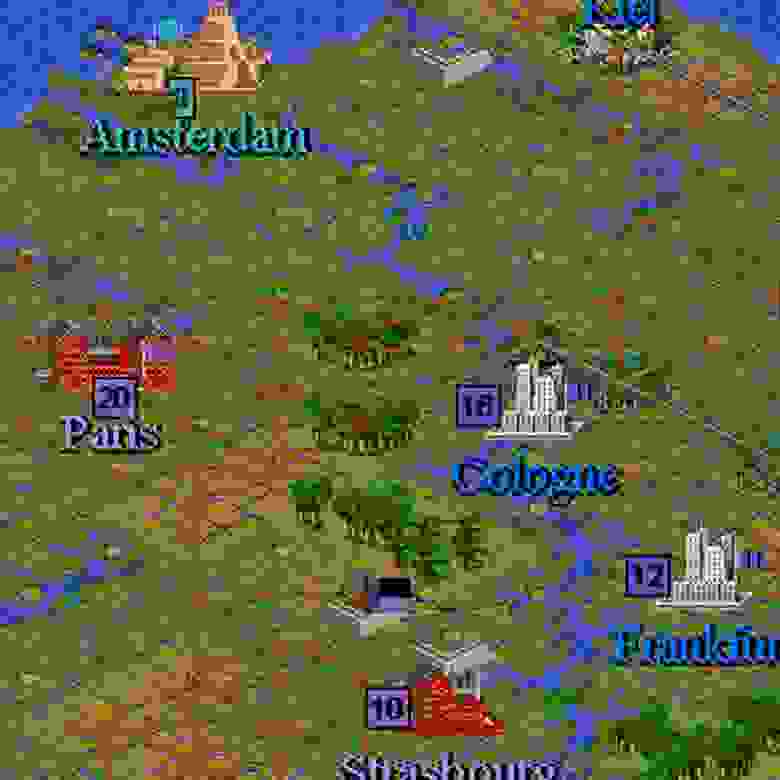
XCOM. Как было и как стало

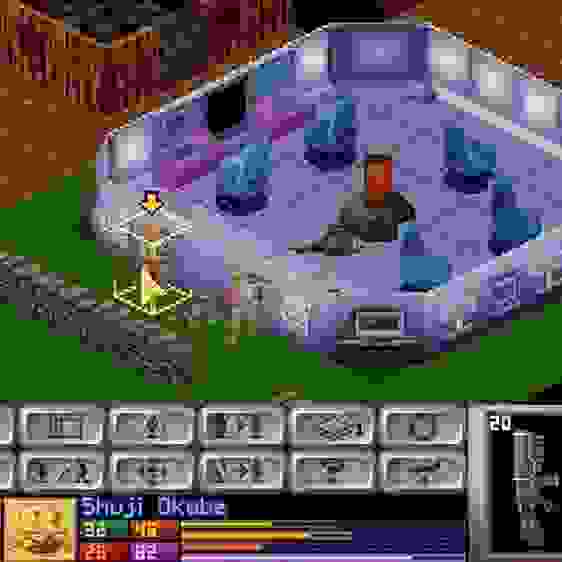
Diablo. Как было и как стало

И новый бум популярности, и неизменную актуальность в новом тысячелетии изометрия приобрела после старта краутфандинговой площадки Kickstarter в 2009г, на которой вскоре стали появляться популярные проекты и в дальнейшем выходить в свет.

К ним можно отнести серию Shadowrun Returns (2013-2015); серии Pillars of Eternity (2015-2018) и Tyranny (2016). Все эти игры были высоко оценены пользователями и все они имели изометрию, тем самым впечатав в мышление игроков, что изометрия — это не отголоски прошлого, а отличное настоящее и не менее хорошее будущее.

Также с помощью Kickstarter было профинансировано и несколько популярных псевдоизометрических 3D-ролевых игр, таких как Divinity: Original Sin (2014) и Wasteland 2 (2014). Однако эти игры отличаются от вышеперечисленных тем, что в них используется перспективная проекция вместо параллельной. Так сказать, Kickstarter вдохнул новую жизнь в изометрические игры, так как ими в основном занимались небольшие компании.

После данного периода большинство изометрических проектов влюбили в себя большое количество игроков. И да, это все было не из-за изометрии в игре, а от того что игры были высочайшего уровня, и изометрия выступала отчасти большим полигоном для экспериментов разработчиков в плане визуальной составляющей и проработке геймплея, которых нельзя было сделать в играх от первого или третьего лица.

А на сегодня все, пишите в комментариях свои изометрические игры, которые вам больше всего запомнились, будет интересно почитать!

Источник