Известно что 12х равен 3 найти 12 2x 1

Контрольная работа Действительные числа

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Контрольная работа №1 Действительные числа

2. Упростить выражение:

5. Записать в виде обыкновенной дроби число 0,3(6).

7. Упростить выражение:

. Записать в виде обыкновенной дроби число 0,(43).

Контрольная работа №1 Действительные числа

Записать в виде обыкновенной дроби число 0,2(7).

Записать в виде обыкновенной дроби число 0,3(1).

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1393609

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Пик использования смартфонов приходится на 16 лет

Время чтения: 1 минута

В Петербурге школьникам разрешили уйти на каникулы с 25 декабря

Время чтения: 2 минуты

Совфед отклонил закон о верифицированных онлайн-платформах и учебниках

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение показательных уравнений.

Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Немного теории.

Показательная функция, её свойства и график

7) a n > 1, если a > 1, n > 0

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение тригонометрических уравнений.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Немного теории.

Тригонометрические уравнения

Уравнение cos(х) = а

Уравнение cos x = а, где \( |a| \leqslant 1 \), имеет на отрезке \( 0 \leqslant x \leqslant \pi \) только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если a

Уравнение sin(х) = а

Уравнение tg(х) = а

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.

Решение тригонометрических уравнений

Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.

Уравнения, сводящиеся к квадратным

Уравнение вида a sin(x) + b cos(x) = c

Используя формулы \( \sin(x) = 2\sin\frac <2>\cos\frac<2>, \; \cos(x) = \cos^2 \frac <2>-\sin^2 \frac <2>\) и записывая правую часть уравпения в виде \( 2 = 2 \cdot 1 = 2 \left( \sin^2 \frac <2>+ \cos^2 \frac <2>\right) \) получаем

В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях \( a \neq 0, \; b \neq 0, \; c \neq 0, \; c^2 \leqslant b^2+c^2 \) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на \( \sqrt \):

Решить уравнение 4 sin(x) + 3 cos(x) = 5

Здесь a = 4, b = 3, \( \sqrt = 5 \). Поделим обе части уравнения на 5:

Уравнения, решаемые разложением левой части на множители

Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.

Источник

Известно что 12х равен 3 найти 12 2x 1

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Решите уравнение

Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.

К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.

Найдите значение выражения при

Объем куба равен Найдите его диагональ.

Прямая является касательной к графику функции Найдите b, учитывая, что абсцисса точки касания больше 0.

Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону где t – время в секундах, амплитуда В, частота /с, фаза Датчик настроен так, что если напряжение в нeм не ниже чем В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

Источник

Решение Ященко ЕГЭ 2022 (профиль) Вариант №6 (36 вариантов) Математика

Решение и ответы заданий Варианта №6 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.

Задание 2.
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °C, равна 0,71. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °C или выше.

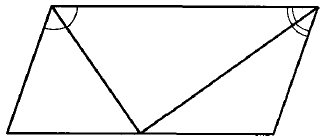
Задание 3.
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 6. Найдите его большую сторону.

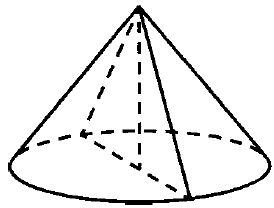
Задание 5.
Диаметр основания конуса равен 32, а длина образующей равна 20. Найдите площадь осевого сечения этого конуса.

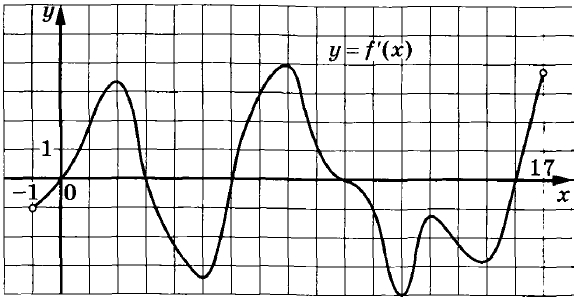
Задание 6.
На рисунке изображён график у = f′(x) – производной функции f(x), определённой на интервале (–9; 6). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Задание 8.
Лодка в 5:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв 2 часа в пункте В, лодка отправилась назад и вернулась в пункт А в 23:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость лодки равна 4 км/ч.

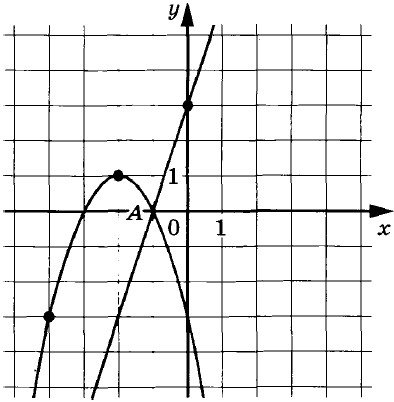
Задание 9.
На рисунке изображены графики функций f(x) = 3x + 3 и g(x) = ax 2 + bх + с, которые пересекаются в точках А(–1; 0) и В(х₀; у₀). Найдите у₀.

Задание 10.
Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а последние 2 раза промахнулся. Результат округлите до сотых.

Задание 11.
Найдите точку минимума функции у = х 3 – 8,5x 2 + 10х – 13.

Задание 12.
а) Решите уравнение cos2x + sin2x + 1 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [3\pi; \frac<9\pi ><2>].

Задание 13.
В правильной призме ABCDA₁B₁C₁D₁ с основанием ABCD боковое ребро равно 2, а сторона основания равна √6. Через точку А₁ перпендикулярно плоскости AB₁D₁ проведена прямая l.

а) Докажите, что прямая l пересекает отрезок АС и делит его в отношении 2:1.
б) Найдите угол между прямыми l и СD₁.

Задание 15.
В июле 2023 года планируется взять кредит на 8 лет в размере 800 тыс. рублей. Условия возврата таковы:
– каждый январь с 2024 по 2027 год долг возрастает на r% по сравнению с концом предыдущего года;
– каждый январь с 2028 по 2031 год долг возрастает на 15 % по сравнению с концом предыдущего года;
– с февраля по июнь необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года;
– к июлю 2031 года кредит должен быть полностью погашен.
Найдите r, если общая сумма выплат по кредиту должна составить 1444 тыс. рублей.

Задание 16.
Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

а) Докажите, что треугольник АОВ прямоугольный.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет \frac<16> <81>площади трапеции ABCD.

Задание 17.
Найдите все такие значения а, при каждом из которых неравенство

верно при всех действительных значениях х.

Задание 18.
Отношение трёхзначного натурального числа к сумме его цифр – целое число.

а) Может ли это отношение быть равным 11?
б) Может ли это отношение быть равным 5?
в) Какое наибольшее значение может принимать это отношение, если число не делится на 100 и его первая цифра равна 7?

Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.

Источник