Известно что аа1 равно вв1 как расположены по отношению друг к другу
Презентация была опубликована 8 лет назад пользователемАлександр Устимов
Похожие презентации
Презентация на тему: » a вектором Отрезок, для которого указано, какой из его концов считается началом, а какой концом, называется вектором АВ ВА a 0 M MM АВ = АВ АВ = АВ MM.» — Транскрипт:
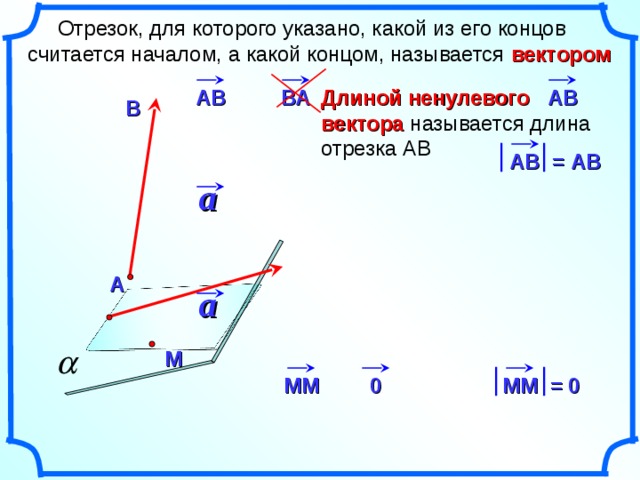
2 a вектором Отрезок, для которого указано, какой из его концов считается началом, а какой концом, называется вектором АВ ВА a 0 M MM АВ = АВ АВ = АВ MM = 0 АВ Длиной ненулевого вектора Длиной ненулевого вектора называется длина отрезка АВАВ
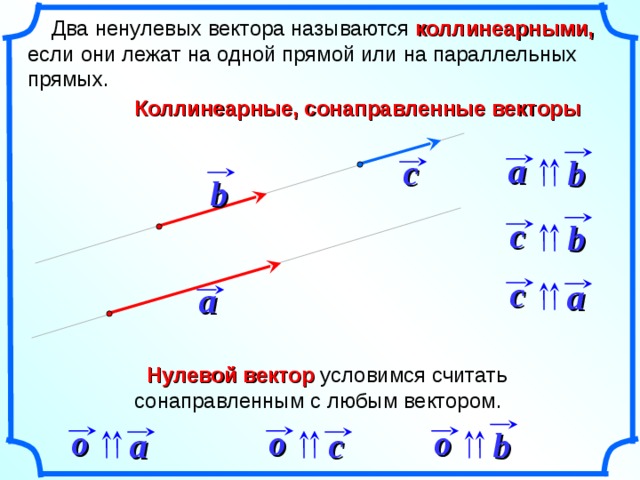
3 коллинеарными, Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. ab c ab ca cb Коллинеарные, сонаправленные векторы oaocob Нулевой вектор Нулевой вектор условимся считать сонаправленным с любым вектором.
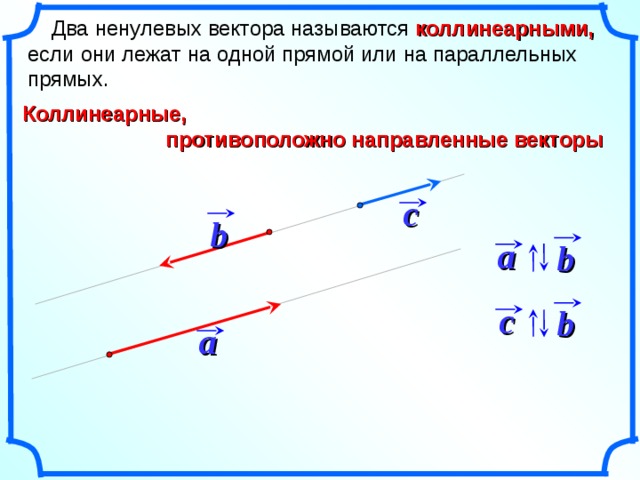
4 коллинеарными, Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.a b c baКоллинеарные, противоположно направленные векторы противоположно направленные векторы bc
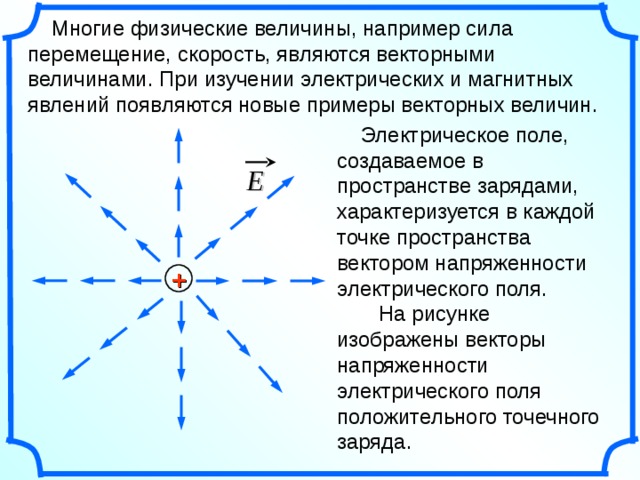
5 Многие физические величины, например сила перемещение, скорость, являются векторными величинами. При изучении электрических и магнитных явлений появляются новые примеры векторных величин. + E Электрическое поле, создаваемое в пространстве зарядами, характеризуется в каждой точке пространства вектором напряженности электрического поля. На рисунке изображены векторы напряженности электрического поля положительного точечного заряда.
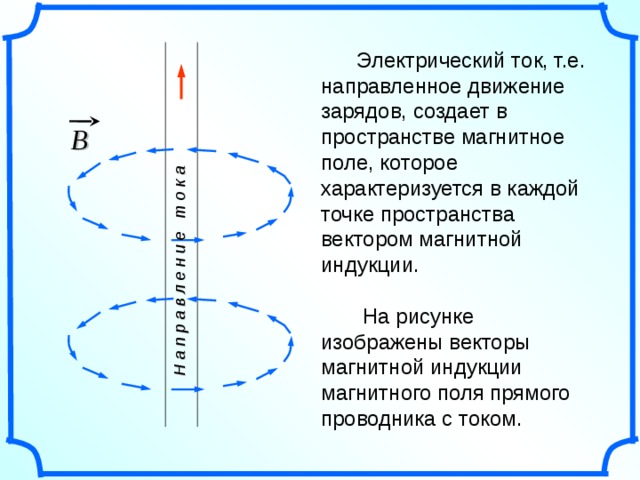
6 Электрический ток, т.е. направленное движение зарядов, создает в пространстве магнитное поле, которое характеризуется в каждой точке пространства вектором магнитной индукции. На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током. B Н а п р а в л е н и е т о к а
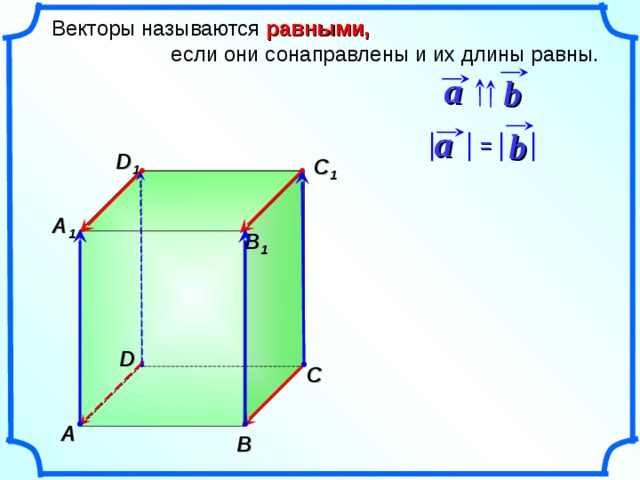
7 A B C A1A1A1A1 B1B1B1B1 C1C1C1C1 D1D1D1D1 ba D равными, Векторы называются равными, если они сонаправлены и их длины равны.ab =
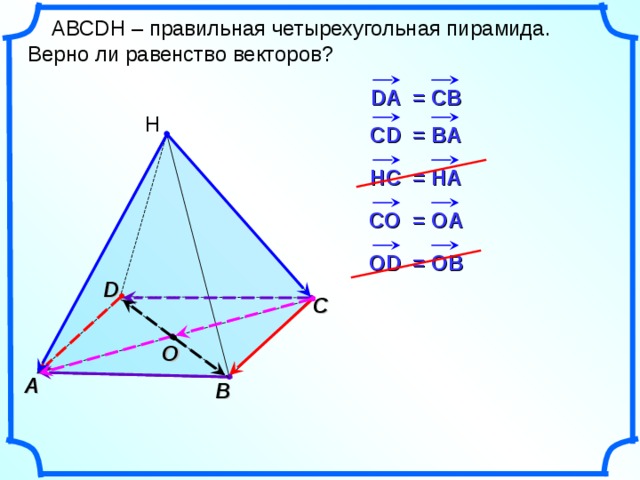
8 D А АВСDH – правильная четырехугольная пирамида. Верно ли равенство векторов? Н В С DA = CB CD = BA HC = HA CO = OA O OD = OB
9 Найдите длины векторов С АВ S D K АВ = 3 ВC = N 4 ВD = 5 M NM = 1,5 BN = 2 NK = 2,5 CB = 4 BA = 3 DB = 5 NC = 2 KN = 2,5
10 На рисунке изображен параллелепипед АВСA 1 B 1 C 1 D 1. Точки М и К – середины ребер В 1 С 1 и А 1 D 1. Укажите на этом рисунке все пары: а) сонаправленных векторов; б) противоположно направленных векторов; в) равных векторов. В А В1В1 С1С1 D1D1 D С K А1А1 M
11 Известно, что АА 1 =ВВ 1. Как расположены по отношению друг к другу: а) прямые АВ и А 1 В; А А1А1 В В1В1 В В1В1 А А1А1
12 Известно, что АА 1 =ВВ 1. Как расположены по отношению друг к другу: б) прямая АВ и плоскость, проходящая через точки А 1 и В 1 ; А А1А1 В В1В1 А А1А1 В В1В1
13 Известно, что АА 1 =ВВ 1. Как расположены по отношению друг к другу: в) плоскости, одна из которых проходит через точки А и В, а другая через точки А 1 и В 1. А1А1 В1В1 А В А А1А1 В В1В1
14 На рисунке изображен параллелепипед АВСA 1 B 1 C 1 D 1. Точки М и К – середины ребер В 1 С 1 и А 1 D 1. Назовите вектор, который получится, если: В А В1В1 С1С1 D1D1 D С K А1А1 M а) от точки С отложить вектор, равный DD 1 ; б) от точки D отложить вектор, равный CM; в) от точки А 1 вектор, равный АС; г) от точки С 1 вектор, равный СВ; г) от точки М вектор, равный КА 1.
15 Сложение векторов. Сложение векторов. Правило треугольника. Правило треугольника.a ab b a + b
16 По правилу треугольника складываются и коллинеарные векторы, хотя при их сложении треугольника и не получаетсяa b a + b a b b
19 Сложение векторов. Правило параллелограмма. a a b b a + b b
21 Сложение векторов. Сложение векторов. Правило треугольника. Правило треугольника. АС = АВ + ВС OB + ВN ON = AR + RS AS = XK + KH XH = MA + AD MD = OF + FP OP =
22 Сложение векторов. Сложение векторов. Правило многоугольника. Правило многоугольника. = АO АВ + ВС + СD + DO a c n m c m n a+c+m+n a
23 Сложение векторов. Сложение векторов. Правило многоугольника. Правило многоугольника. = А 1 A 7 A1A1 A2A2 A3A3 A4A4 A5A5 A6A6 A7A7 А 1 A 2 + A 2 A 3 + A 3 A 4 + A 4 A 5 +A 5 A 6 +A 6 A 7
24 Умножение вектора на число. a bka2b 2bb b2b2= 2 a1 2 a1a 2 a1a 21=
0 b k» title=»Для любого числа и любого вектора векторы и коллинеарны. ak aka Произведением ненулевого вектора на число называется такой вектор, длина которого равна, причем векторы и сонаправлены при и притивоположно направлены при. ak a b a k k>0 b k» > 25 Для любого числа и любого вектора векторы и коллинеарны. ak aka Произведением ненулевого вектора на число называется такой вектор, длина которого равна, причем векторы и сонаправлены при и притивоположно направлены при. ak a b a k k>0 b k 0 b k»> 0 b k»> 0 b k» title=»Для любого числа и любого вектора векторы и коллинеарны. ak aka Произведением ненулевого вектора на число называется такой вектор, длина которого равна, причем векторы и сонаправлены при и притивоположно направлены при. ak a b a k k>0 b k»>
26 Умножение вектора на число. Произведение любого вектора на число нуль есть нулевой вектор. k (l a) o a o = (kl)a = Сочетательный закон Первый распределительный закон Второй распределительный закон k (a + b) = ka + kb (k+l)a = ka + la Для любых, и любых чисел, справедливы равенства:abbkl Произведение нулевого вектора на любое число считается нулевой вектор. o o k =
28 Диагонали параллелепипеда АВСDА 1 В 1 С 1 D 1 пересекаются в точке О. При каком значении справедливо соотношение k A B C A1A1A1A1 B1B1B1B1 C1C1C1C1 D1D1D1D1 D O 2 1k АВ + В 1 С 1 + СО = С 1 A АВ + В 1 С 1 + СО = АВ + ВС + СО = ВС АОk С 1 A С 1 A=
Конспект и презентация к уроку геометрии в 10 классе «Векторы в пространстве»
Конспект и презентация к уроку геометрии в 10 классе «Векторы в пространстве»
Просмотр содержимого документа
«Конспект и презентация к уроку геометрии в 10 классе «Векторы в пространстве»»
Отрезок, для которого указано, какой из его концов считается началом, а какой концом, называется вектором
Длиной ненулевого вектора называется длина отрезка АВ
«Геометрия 10-11» Л.С. Атанасян и др.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Коллинеарные, сонаправленные векторы
«Геометрия 10-11» Л.С. Атанасян и др.
Нулевой вектор условимся считать сонаправленным с любым вектором.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
противоположно направленные векторы
«Геометрия 10-11» Л.С. Атанасян и др.
Многие физические величины, например сила перемещение, скорость, являются векторными величинами. При изучении электрических и магнитных явлений появляются новые примеры векторных величин.
Электрическое поле, создаваемое в пространстве зарядами, характеризуется в каждой точке пространства вектором напряженности электрического поля.
На рисунке изображены векторы напряженности электрического поля положительного точечного заряда.
«Геометрия 10-11» Л.С. Атанасян и др.
Н а п р а в л е н и е т о к а
Электрический ток, т.е. направленное движение зарядов, создает в пространстве магнитное поле, которое характеризуется в каждой точке пространства вектором магнитной индукции.
На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током.
«Геометрия 10-11» Л.С. Атанасян и др.
Векторы называются равными,
если они сонаправлены и их длины равны.
«Геометрия 10-11» Л.С. Атанасян и др. Рисунки Савченко Е.М.
АВС DH – правильная четырехугольная пирамида.
Известно что аа1 равно вв1 как расположены по отношению друг к другу
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
а) Известно, что медианы треугольника точкой пересечения делятся в отношении 2 : 1, считая от вершины. Значит,
Поэтому треугольники AB1B и CB1B равнобедренные, причём ∠B1AB = ∠ABB1 и ∠B1CB = ∠CBB1. Сумма всех этих четырёх углов равна 180°. Тогда ∠ABC = ∠ABB1 + ∠CBB1 = 90°. Отсюда следует, что треугольник ABC прямоугольный.
б) Треугольник A1BA прямоугольный. Поэтому
Аналогично, из прямоугольного треугольника C1BC находим:
Сложим полученные равенства:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Аналоги к заданию № 505537: 509323 509344 511579 Все
Доказать можно проще:
Треугольник — равнобедренный,
— высота треугольника
— средняя линия треугольника
Значит по теореме о перпендикулярности прямой, параллельной перпендикуляру.
Можно еще проще. значит
— центр описанной окружности, а
— ее диаметр. Угол
— прямой, как опирающийся на диаметр.
Известно что аа1 равно вв1 как расположены по отношению друг к другу
На ребре BB1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка F так, что B1F : FB = 3 : 4. Точка T — середина ребра B1C1. Известно, что AD = 12, AA1 = 14.
а) Докажите, что плоскость FTD1 делит ребро AA1 в отношении 6 : 1.
б) Найдите площадь сечения параллелепипеда плоскостью FTD1.
б) Трапеция ED1TF — сечение параллелепипеда плоскостью ETD1. Найдём стороны трапеции:
Следовательно, трапеция ED1TF — равнобедренная. Найдём высоту трапеции:
Тогда площадь трапеции равна
Ответ: б)