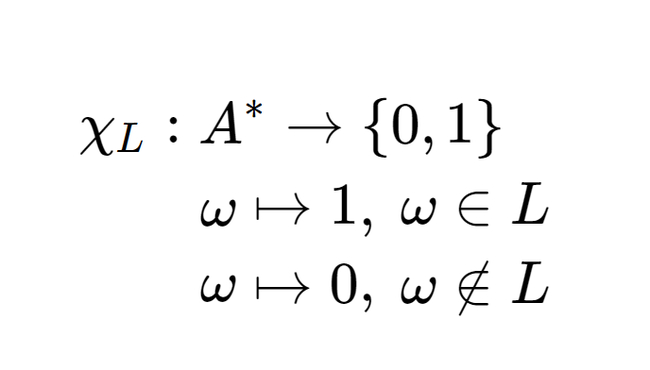Известно что березы деревья также

Известно что березы деревья также

В городе Z в 2013 году мальчиков родилось больше, чем девочек. Мальчиков чаще всего называли Андрей, а девочек — Мария. Выберите утверждения, которые следуют из приведённых данных.

Среди рождённых в 2013 году в городе Z:

1) девочек с именем Мария больше, чем с именем Светлана.

2) мальчиков с именем Николай больше, чем с именем Аристарх.

3) хотя бы одного из родившихся мальчиков назвали Андреем.

4) мальчиков с именем Андрей больше, чем девочек с именем Мария.

В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

1) Утверждение о том, что девочек чаще всего называли Мария означает, что девочек, которых называли другими именами меньше, следовательно, первое утверждение верно. Первое утверждение следует из приведённых данных.

2) Второе утверждение не следует из приведённых данных.

3) Если мальчиков чаще всего называли Андреями, то, следовательно, родился по крайней мере один мальчик, которого назвали Андреем. Третье утверждение следует из приведённых данных.

4) Четвёртое утверждение не следует из приведённых данных, поскольку невозможно сказать, сколько родившихся мальчиков назвали Андреями, а сколько девочек — Мариями.

Игорь Витальевич часто ездит на работу на велосипеде. Он не ездит на велосипеде в те дни, когда идёт дождь или снег, а также по четвергам, когда Игорь Витальевич надевает парадный костюм. Выберите утверждения, которые верны при приведённых условиях.

1) Сегодня Игорь Витальевич приехал на работу на велосипеде, значит, сегодня нет дождя.

2) Каждый раз, когда в течение дня будет ясно, Игорь Витальевич будет добираться на работу на велосипеде.

3) Каждый раз, когда Игорь Витальевич добирается до работы без велосипеда, он одет в парадный костюм.

4) Каждый раз, когда на улице идёт снег, Игорь Витальевич добирается до работы без велосипеда.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Проанализируем представленные утверждения, исходя из условий задачи.

1) Игорь Витальевич не ездит на велосипеде в те дни, когда идёт дождь. Утверждение верно.

2) Игорь Витальевич не ездит на велосипеде по четвергам, когда надевает парадный костюм, следовательно, даже если в четверг будет ясно, Игорь Витальевич не поедет на работу на велосипеде. Утверждение неверно.

3) Не всегда, Игорь Витальевич также не ездит на велосипеде в те дни, когда идёт дождь или снег. Утверждение неверно.

4) Игорь Витальевич не ездит на велосипеде в те дни, когда идёт снег. Утверждение верно.

В классе учатся 20 человек, из них 13 человек посещают кружок по истории, а 10 человек — кружок по математике. Выберите утверждения, которые следуют из приведённых данных. В этом классе

1) нет ученика, который не посещает ни кружок по истории, ни кружок по математике

2) найдутся хотя бы два человека, которые посещают оба кружка

3) если ученик не ходит на кружок по истории, то он обязательно ходит на кружок по математике

4) не найдётся 11 человек, которые посещают оба кружка

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

1) Утверждение не следует из приведённых данных, поскольку возможна ситуация, когда из 13 человек, посещающих кружок по истории, десять человек посещают ещё и кружок по математике, а оставшиеся семь учеников класса не посещают ни один кружок.

2) Утверждение следует из приведённых данных. Более того, можно утверждать, что минимум три человека посещают сразу оба кружка, поскольку суммарное количество учеников, посещающих кружки, на 3 больше количества учеников в классе.

3) Утверждение не следует из приведённых данных, поскольку возможна ситуация, когда 10 человек из тринадцати, посещающих кружок по истории ходят и на кружок по математике. При этом окажется, что семь человек не посещают ни одного кружка.

4) Кружок по математике посещают 10 человек, поэтому более 10 человек посещать оба кружка не может. Утверждение верно.

Источник

О современном образовании

Задали мне сегодня задачку:

В роще растут деревья четырёх видов: берёзы, ели, сосны и осины. Всего 100 деревьев. Известно, что среди любых 85 деревьев найдутся деревья всех четырех видов. Среди какого наименьшего количества любых деревьев в этой роще обязательно найдутся деревья хотя бы трёх видов?

Кстати правильного ответа я не знаю. Чисто логически тут ответ 3. Мы можем наугад тыкнуть в 3 дерева и как попасть на 3 абсолютно разных, так и собрать 3 одинаковых. Но задача по математике, поэтому тут число 85 намекает на то, что минимальное число дерева каждого вида 16 штук, чтобы мы гарантированно получили в выборке 4 вида. На 3 вида думаю это задача на дроби. Однако задача уже априори имеет как минимум 2 варианта ответа, и оба они верные. Не знаю, когда учился я в школе, таких разночтений не позволяли

1) Необходимость. Докажем, что меньше нельзя. Например, 68 деревьев. Очевидно, что распределение 34-34-16-16 удовлетворяет исходному условию (среди 85 есть все 4 вида), а взяв первые два вида, получим 68 деревьев. То есть, 68 не является достаточным набором.

Мы можем наугад тыкнуть в 3 дерева и как попасть на 3 абсолютно разных, так и собрать 3 одинаковых.

Ключевое слово «обязательно». Поэтому ваш чисто логичный ответ 3 не подходит.

Известно, что среди любых 85 деревьев найдутся деревья всех четырех видов.

Мы выбираем 85 деревьев, остается не выбранными 15.

Значит, если каждого дерева 16 и больше, то без варианта выберешь хоть одно дерево.

Если мы выбираем деревья так, чтобы внутри выборки оказалось не менее 3 видов деревьев», то в худшем случае имеем:

X + 16 + 15 = 100 (мы не выбрали целиком один вид и не выбрали почти все деревья второго вида).

херне учат, задачи должны быть с экономическим уклоном типа; мойша дал ване денег в кредит

Вы не умеете читать задачу. От вас требуется найти МИНИМАЛЬНОЕ количество деревьев среди которых ОБЯЗАТЕЛЬНО будет три разных.

Если взять самый простой пример и раскидать деревья по 25 каждого, то станет понятно что мы легко можем набрать 25 деревьев одного вида, если мы добираем 26 то там уже будет обязательно два вида деревьев (сий очевидный факт называется «Принцип Дирихле»). В нашем примере чтобы гарантированно иметь три вида деревьев в выборке их нужно взять 51 штуку.

Вернемся к общему кейсу, предположим что у нас ровно по 16 деревьев трех видов, тогда на четвертый останется 52 дерева, в таком случае чтобы получить множество гарантированно содержащее 3 вида нужно взять 69 деревьев (и это ответ). Покажем что для любого другого распределения мы тоже будем иметь три вида деревьев в выборке объемом 69:
Пусть это не так, тогда на оставшиеся 31 дерево будет содержать все деревья как минимум двух видов, но если одного из видов там хотя бы 16, то 16 второго уже точно не наберется, что противоречит условию

Там же в условии обезательно 3 вида, если взять тот дерева, то ни о каком «обезательно» речи идти не может

История проблемы равенства классов P и NP

В 2000 году Математический институт Клэя определил 7 математических задач, решение которых не могли найти в течение многих лет. За решение каждой из них была назначена награда в размере 1 миллиона долларов. Эти 7 задач известны как «задачи тысячелетия», и на сегодняшний день только одна из них была решена — гипотеза Пуанкаре. В этой статье пойдет речь о вопросе равенства классов P и NP, ответ на который может сильно повлиять на всю IT-сферу.

Равенство P и NP классов отсылает нас к теории алгоритмов, а именно к классам сложности. Первое, с чего стоит начать, это то, что классы P и NP классифицируют языки, а не задачи. Пока что это звучит довольно абсурдно, поэтому для понимания разберемся в некоторых деталях.

Пусть А — алфавит и L ⊆ А*, тогда L называется языком над А. Для любого алфавита пустое множество и А* являются тривиальными языками. При этом пустое множество часто называют пустым языком. Однако не стоит путать пустой язык и язык, содержащий пустое слово e, — они различны. Языки могут быть как бесконечными, так и нет, но обязательно счетными. Т. е. множество всех действительных чисел языком нельзя назвать, т. к. такой набор является неисчисляемым.

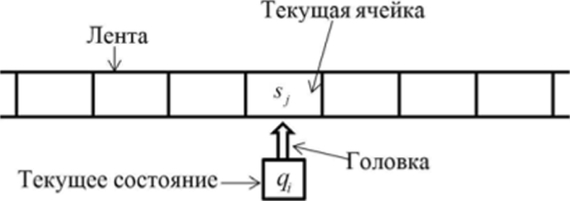
Говоря про абстрактный исполнитель, чаще всего имеют в виду машину Тьюринга, поэтому в дальнейшем под АИ будем подразумевать именно её. Итак, машина Тьюринга имеет неограниченное линейное хранилище, сгруппированное в ячейки. Каждая ячейка может содержать ровно один символ алфавита в любой момент времени. Вдоль ячеек идет считывающая головка, имеющая конечное число состояний. За одну итерацию она может считать значение только одной ячейки, переписать её значение, изменить свое состояние и перейти на одну позицию вправо/влево.

Устройство машины Тьюринга

На основе машины Тьюринга определим так называемую разрешающую машину над языком. Для начала введем определение характеризующей функции X(w). Функция X определяет, принадлежит ли слово w языку L. Если да, то значение функции равно «1»; если нет, то «0». Формально это можно записать так:

Разрешающей машиной D для языка L называется такая машина, которая для каждого w∈A вычисляет характеризующую функцию X(w) за конечное время.

В дополнение к разрешающей машине идет верификатор. Машина V, которая принимает слова w и c и выводит 0 или 1 после конечного числа шагов, называется верификатором для L, если она обладает следующими свойствами:

— выводит 1, только если w входит в язык L;

— для любого w в языке L существует такое c, что V(w,c) = 1.

Классы сложности и формулировка проблемы

Окей, мы рассмотрели несколько понятий. На первый взгляд, все это больше походит на лингвистику: алфавиты, слова, языки… Причем тут задачи? Чтобы ответить на этот вопрос, обратимся к понятию задача разрешимости (англ. Decision problem). Это такой вопрос (сформулированный в формальной системе), требующий ответа «да» или «нет», зависящего, возможно, от значений некоторых входных параметров. Например, «является ли данное натуральное число x простым?» или «даны два числа: x и y; делится ли x на y?« Метод решения в виде алгоритма называется разрешающей процедурой. Теория вычислимости имеет дело в основном с задачами разрешимости и приведенные выше конструкции наглядно соотносятся с таким типом задач: так разрешающая машина над языком является формализацией разрешающей процедуры. Но как же быть с задачами, такими как задача коммивояжера? На них нельзя дать бинарный ответ. В таких случаях применяют приемы приведения к версии decision problem. В случае коммивояжера проблема по-новому формулируется так: «существует ли маршрут не длиннее, чем заданное значение k?»

В класс сложности NP входят все языки L, для которых существует такой верификатор, что для каждого (w,c) время его работы полиномиально. Иными словами, NP включает в себя задачи разрешимости, для которых при подходящем сертификате для данного w мы быстро сможем удостовериться в том, что w действительно принадлежит L (ответ на вопрос можно довольно быстро проверить). Отсюда и название «верификатор». В качестве примера задачи в NP можно привести определение наличия в графе гамильтонова цикла. Сертификат в данном случае — последовательность вершин, образующих гамильтонов цикл.

Помимо этих классов можно выделить ещё 2: NP-hard и NP-Complete. Они основываются на приводимости одного языка к другому за полиномиальное время: пусть языки A и B — языки над одним алфавитом. Язык А будет приводимым за полиномиальное время к языку B, если существует такая функция f(w), что

— функция f может быть вычислена машиной Тьюринга за полиномиальное время.

Тогда в класс NP-hard будут входить языки, к которым приводимы все языки в NP (причем NP-hard язык может входить в NP, а может и нет), а в NP-Complete те языки, которые являются одновременно NP-hard и NP. Примером NP-Complete является язык выполнимых булевых формул (SAT). Таким образом, NP-Complete задачи образуют в некотором смысле подмножество «типовых» задач в классе NP: если для какой-то из них найден «полиномиально быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».

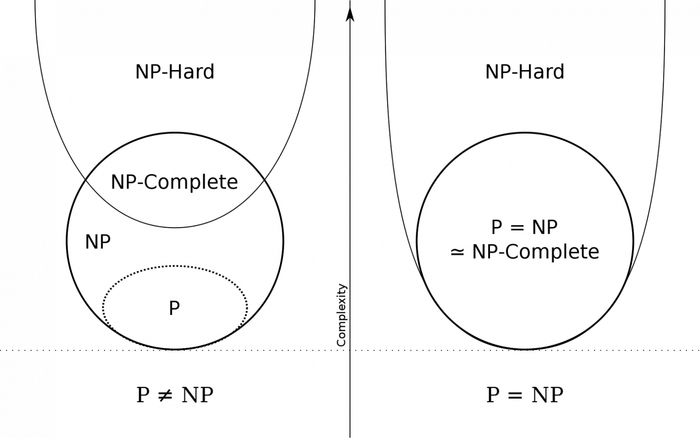
Отношение между классами при равенстве и неравенстве

Теперь, немного погрузившись в теорию алгоритмов, более конкретно обозначим проблему равенства данных классов. Итак, множество P входит в множество NP, но неизвестно, существуют ли языки, которые входят в NP и не входят в P. Что это означает на практике? Итак, простыми словами класс NP можно охарактеризовать как «трудно решить, легко проверить». Классическим примером задачи, входящей в NP, является задача коммивояжера, для решения которой на данный момент известен лишь один алгоритм — старый добрый перебор (мы не рассматриваем эвристические методы). Однако, получив ответ, его будет не так сложно проверить. Класс P же вобрал в себя те задачи, для которых существует эффективный алгоритм решения, позволяющий решать их за полиномиальное время. И равенство или, наоборот, неравенство этих классов пока не доказано. Если эти классы равны, то это будет значить, что для всех задач, которые сейчас решаются путем перебора или другим неэффективным методом, существует(-ют) полиномиальные алгоритмы. А если не равны, то придется смириться с неоптимальностью решения этих задач.

История проблемы равенства P и NP началась в 1928 году, когда Давид Гильберт сформулировал проблему, названную Entscheidungsproblem (нем. задача разрешения). Ее суть заключается в нахождении алгоритма, определяющего доказуемость данного утверждения из аксиом с использованием правил логики. По названию очевидно, что это задача является задачей разрешения (выводит «да» или «нет»).

В ходе решения этой проблемы потребовалось определить термины «алгоритм» и «вычислимая функция». В 1936 году Алонзо Чёрч и Алан Тьюринг независимо показали, что общее решение Entscheidungsproblem невозможно, предположив, что интуитивное понятие «эффективная вычислимость» соответствует вычислимости функции на машине Тьюринга. Эта гипотеза сегодня известна как тезис Чёрча-Тьюринга.

20 марта 1956 в письме к Джону фон Нейману Курт Гёдель впервые поставил вопрос о вычислительной сложности. Гёдель интересовался, можно ли получить доказательство теоремы (в математико-логическом смысле слова) за квадратичное или линейное время. К сожалению, письмо было обнаружено лишь в 1989 году и получило широкую огласку, когда Юрис Хартманис опубликовал перевод и комментарий.

Статья Алана Кобэма 1965 года под названием «The intrinsic computational difficulty of functions» является одним из первых упоминаний класса сложности P, состоящего из разрешимых за полиномиальное время задач. Тезис Кобэма-Эдмондса (известный также как расширенный тезис Чёрча-Тьюринга), названный в честь Алана Кобэма и Джека Эдмондса, утверждает, что любая разумная модель вычислений может быть выражена через другую модель с замедлением, не более чем полиномиальным по размеру входных данных. Кобэм предположил, что класс P может быть хорошим способом для описания множества реально вычислимых задач. Любая проблема, не содержащаяся в P, невозможна, но если задача реального мира может быть решена с помощью алгоритма, существующего в P, то такой алгоритм в конечном итоге будет открыт.

В 1965 году Юрис Хартманис и Ричард Стернс опубликовали статью «On the Computational Complexity of Algorithms», отмеченную премией Тьюринга. В ней даются более точные определения сложности алгоритма и класса сложности. Хартманис и Стернс определили класс сложности как совокупность всех задач, которые можно решить за установленные временные рамки. В их статье показано, что существует бесконечная иерархия классов сложности (например, задачи, для которых наиболее быстрый алгоритм имеет время, пропорциональное n, n log n, n^2, n^3, 2^n и т. д.), где небольшое увеличение временного интервала позволяет решать больше задач. Во второй статье Хартманис совместно с Филипом М. Льюисом показали, что подобная иерархия существует и для количества памяти (функция от размера входа) при решении задачи на машине Тьюринга.

В 1967 году Мануэль Блюм разработал аксиоматическую теорию сложности, которая основана на его собственных аксиомах (аксиомы Блюма), и получил важный результат — теорему об ускорении. До этого мы говорили по большей части о сложности алгоритма. Хотелось бы аналогичным образом определить и сложность задачи: например, какова сложность самого эффективного (по времени и емкости) алгоритма, решающего эту задачу. Теорема об ускорении гласит, что есть некоторые задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм.

Точная формулировка проблемы равенства P и NP была представлена в 1971 году. Тогда американский ученый Стивен Кук и работавший независимо советский ученый Леонид Левин доказали, что существуют практически актуальные проблемы, которые являются NP-полными. В США Стивен Кук опубликовал статью «The complexity of theorem proving procedures», в которой формализовал понятия редукции за полиномиальное время и NP-полноты, а также доказал существование NP-полной задачи (задача выполнимости булевых формул, SAT). Теорема была независимо доказана Леонидом Левиным и, таким образом, получила название «теорема Кука-Левина».

В 1972 году Ричард Карп сделал рывок в знаменитой статье «Reducibility among Combinatorial Problems», в которой показал, что около 20 разнообразных задач из комбинаторики и теории графов, известных своей вычислительной трудностью, являются NP-полными.

В августе 2010 года Виней Деолаликар, работавший в исследовательском отделении Hewlett-Packard в Пало-Альто в Калифорнии, заявил, что разгадал загадку P vs NP. Он утверждал, что P не равняется NP, однако научное сообщество нашло в его доказательстве фатальную ошибку. В начале 2002 года SIGACT News провел опрос среди 100 ученых, задав им вопрос о равенстве классов NP и P. 61 человек ответили, что «неравны», 9 — «равны», 22 затруднились ответить и 8 сказали, что гипотеза не выводима из текущей системы аксиом и, таким образом, не может быть доказана или опровергнута.

К чему приведет решение проблемы

Окей, теория вычислимости, формализация алгоритмов и абстрактные математические теории — все это конечно интересно, но как решение проблемы равенства NP и P классов отразится на практике? На самом деле, алгоритмы для решения NP-задач используются каждый день во многих сферах. Например, в криптографии, криптовалютах, восстановлении поврежденных файлов, системах блокировки спама, оптимизации в логистике и т. д. Более эффективные решения могли бы значительно сэкономить время и деньги, так как мы пользуемся в основном эвристическими методами, дающими лишь приближенные решения.

Однако существует и обратная сторона монеты. Солидная часть криптографии (криптосистемы с открытым ключом, технологии доказательства выполнения работы в блокчейне, системы блокировки спама) основывается на предположении о неравенстве NP и P классов. Если окажется, что некоторые задачи, для которых, как считалось, не существует эффективных алгоритмов, можно решать быстро, то многие методы защиты устареют.

Может оказаться и так, что последствия решения окажутся не такими тривиальными, как это часто и бывает в математике. В качестве примера рассмотрим континуум-гипотезу о существовании мощности, меньшей континуума и большей мощности счетного множества. Оказывается, существование такого кардинала нельзя ни доказать, ни опровергнуть в аксиоматике ZFC. Так что мы вправе считать, что такие мощности бывают (впрочем, как и считать, что не бывают). Однако ясно, что мы не можем конструктивно построить соответствующее множество. Возможно, точно также окажется и с алгоритмами для NP-задач в случае равенства NP и P (к слову, некоторые математики в опросе SIGACT News так и ответили: гипотеза не выводима из существующей системы аксиом, то есть не может быть доказана или опровергнута).

Пока что существующих методов доказательств недостаточно для строго математического ответа, но не нужно терять надежду. В марте 2001 года Ричард Карп предсказал, что проблема будет решена молодым математиком (до 30 лет) с использованием подхода, о котором еще никто не думал. Стивен Кук заявил, что кто-нибудь предоставит убедительное доказательство в ближайшие 20 лет.

Источник

Тренировочная работа 11 класс для подготовки к ЕГЭ по теме «Задачи»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Стоимость проездного билета на месяц составляет 750 рублей, а стоимость билета на одну поездку — 19 рублей. Аня купила проездной и сделала за месяц 45 поездок. На сколько рублей больше она бы потратила, если бы покупала билеты на одну поездку?

При взве­ши­ва­нии жи­вот­ных в зоо­пар­ке вы­яс­ни­лось, что жираф тя­же­лее вер­блю­да, вер­блюд тя­же­лее тигра, а лео­пард легче вер­блю­да. Вы­бе­ри­те утвер­жде­ния, ко­то­рые верны при ука­зан­ных усло­ви­ях.

1) лео­пард тя­же­лее вер­блю­да

2) жираф тя­же­лее лео­пар­да

3) жираф легче тигра

4) жираф самый тяжёлый из всех этих жи­вот­ных

Вычеркните в числе 85417627 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите ровно одно получившееся число

Куз­не­чик пры­га­ет вдоль ко­ор­ди­нат­ной пря­мой в любом на­прав­ле­нии на еди­нич­ный от­ре­зок за один пры­жок. Куз­не­чик на­чи­на­ет пры­гать из на­ча­ла ко­ор­ди­нат. Сколь­ко су­ще­ству­ет раз­лич­ных точек на ко­ор­ди­нат­ной пря­мой, в ко­то­рых куз­не­чик может ока­зать­ся, сде­лав ровно 11 прыж­ков?

Опто­вая цена учеб­ни­ка 170 руб­лей. Роз­нич­ная цена на 20% выше опто­вой. Какое наи­боль­шее число таких учеб­ни­ков можно ку­пить по роз­нич­ной цене на 7000 руб­лей?

Чтобы связать свитер, хозяйке нужно 900 граммов шерсти синего цвета. Можно купить синюю пряжу по цене 70 рублей за 100 г, а можно купить неокрашенную пряжу по цене 60 рублей за 100 г и окрасить её. Один пакетик краски стоит 40 рублей и рассчитан на окраску 300 г пряжи. Какой вариант покупки дешевле? В ответ напишите, сколько рублей будет стоить эта покупка.

В среднем из 900 садовых насосов, поступивших в продажу, 27 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Летом килограмм клубники стоит 90 рублей. Маша купила 1 кг 200 г клубники. Сколько рублей сдачи она должна была получить с 500 рублей?

Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. После удер­жа­ния на­ло­га на до­хо­ды Мария Кон­стан­ти­нов­на по­лу­чи­ла 9570 руб­лей. Сколь­ко руб­лей со­став­ля­ет за­ра­бот­ная плата Марии Кон­стан­ти­нов­ны?

При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 9 тонн природного камня и 13 мешков цемента. Для бетонного фундамента необходимо 8 тонн щебня и 57 мешков цемента. Тонна камня стоит 1700 рублей, щебень стоит 700 рублей за тонну, а мешок цемента стоит 220 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешёвый вариант?

На зим­ней олим­пиа­де сбор­ная Ка­на­ды за­во­е­ва­ла ме­да­лей боль­ше, чем сбор­ная Ни­дер­лан­дов, сбор­ная Бе­ла­ру­си — мень­ше, чем сбор­ная Ни­дер­лан­дов, а сбор­ная Швей­ца­рии мень­ше, чем сбор­ная Ка­на­ды. Вы­бе­ри­те утвер­жде­ния, ко­то­рые сле­ду­ют из при­ведённых дан­ных.

1) Из на­зван­ных сбор­ных ко­ман­да Швей­ца­рии за­ня­ла вто­рое место.

2) Сбор­ная Бе­ла­ру­си за­во­е­ва­ла мень­ше ме­да­лей, чем сбор­ная Ка­на­ды.

3) Среди на­зван­ных сбор­ных точно нет двух, за­во­е­вав­ших рав­ное ко­ли­че­ство ме­да­лей.

4) Сбор­ная Ка­на­ды за­во­е­ва­ла боль­ше ме­да­лей, чем каж­дая из осталь­ных трёх сбор­ных.

В от­ве­те за­пи­ши­те но­ме­ра вы­бран­ных утвер­жде­ний без про­бе­лов, за­пя­тых и дру­гих до­пол­ни­тель­ных сим­во­лов.

5. В кор­зи­не лежит 40 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 17 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 25 гри­бов хотя бы один груздь. Сколь­ко ры­жи­ков в кор­зи­не?

Приведите пример трёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.

7. Конкурс исполнителей проводится в 3 дня. Всего заявлено 80 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 16 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса?

На счету Юлиного мобильного телефона был 71 рубль, а после разговора с Мишей осталось 47 рублей. Сколько минут длился разговор с Мишей, если одна минута разговора стоит 1 рубль 50 копеек.

В таблице указаны средние цены (в рублях) на некоторые основные продукты питания в трёх городах России (по данным на начало 2010 года).

Пшеничный хлеб (батон)

Мясо (говядина, 1 кг)

Подсолнечное масло (1 литр)

Определите, в каком из этих городов окажется самым дешёвым следующий набор продуктов:

3 батона пшеничного хлеба, 3 кг картофеля, 1 л подсолнечного масла. В ответ запишите стоимость данного набора продуктов в этом городе (в рублях).

В школе 124 уче­ни­ка изу­ча­ют фран­цуз­ский язык, что со­став­ля­ет 25% от числа всех уче­ни­ков. Сколь­ко уче­ни­ков учит­ся в школе?

В клас­се учит­ся 20 че­ло­век, из них 13 че­ло­век по­се­ща­ют кру­жок по ис­то­рии, а 10 — кру­жок по ма­те­ма­ти­ке. Вы­бе­ри­те утвер­жде­ния, ко­то­рые верны при ука­зан­ных усло­ви­ях.

1) Каж­дый уче­ник этого клас­са по­се­ща­ет оба круж­ка.

2) Най­дут­ся хотя бы двое из этого клас­са, кто по­се­ща­ет оба круж­ка.

3) Если уче­ник из этого клас­са ходит на кру­жок по ис­то­рии, то он обя­за­тель­но ходит на кру­жок по ма­те­ма­ти­ке.

4) Не найдётся 11 че­ло­век из этого клас­са, ко­то­рые по­се­ща­ют оба круж­ка. В от­ве­те за­пи­ши­те но­ме­ра вы­бран­ных утвер­жде­ний без про­бе­лов, за­пя­тых и дру­гих до­пол­ни­тель­ных сим­во­лов.

5. В пер­вом ряду ки­но­за­ла 24 места, а в каж­дом сле­ду­ю­щем на 2 боль­ше, чем в преды­ду­щем. Сколь­ко мест в вось­мом ряду?

6. Вычеркните в числе 123456 три цифры так, чтобы получившееся трёхзначное число делилось на 27. В ответе укажите получившееся число

7. Тоня, Арина, Маша, Денис, Лёня и Максим бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка.

В школе есть пятиместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвует 26 человек?

Для группы иностранных гостей требуется купить 10 путеводителей. Нужные путеводители нашлись в трёх интернет-магазинах. Цена путеводителя и условия доставки всей покупки приведены в таблице.

Цена путеводителя (руб. за шт.)

Стоимость доставки (руб.)

Доставка бесплатно, если сумма заказа превышает 3000 руб.

Доставка бесплатно, если сумма заказа превышает 2500 руб.

Во сколько рублей обойдётся наиболее дешёвый вариант покупки с доставкой?

3. На олимпиаде по химии 400 участников разместили в трёх аудиториях. В первых двух удалось разместить по 150 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.

4. Мо­биль­ный те­ле­фон стоил 3500 руб­лей. Через не­ко­то­рое время цену на эту мо­дель сни­зи­ли до 2800 руб­лей. На сколь­ко про­цен­тов была сни­же­на цена?

5. Из­вест­но, что берёзы — де­ре­вья, также из­вест­но, что все де­ре­вья вы­де­ля­ют кис­ло­род. Под­сол­ну­хи тоже вы­де­ля­ют кис­ло­род. Вы­бе­ри­те утвер­жде­ния, ко­то­рые сле­ду­ют из при­ведённых дан­ных.

1) Все берёзы вы­де­ля­ют кис­ло­род

2) Все под­сол­ну­хи яв­ля­ют­ся берёзами

3) Не­ко­то­рые рас­те­ния, вы­де­ля­ю­щие кис­ло­род, яв­ля­ют­ся берёзами

4) Если рас­те­ние не вы­де­ля­ет кис­ло­род, то оно — не под­сол­нух

В от­ве­те ука­жи­те но­ме­ра вы­бран­ных утвер­жде­ний без про­бе­лов, за­пя­тых и дру­гих до­пол­ни­тель­ных сим­во­лов.

6. В кор­зи­не лежит 50 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 28 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 24 гри­бов хотя бы один груздь. Сколь­ко груз­дей в кор­зи­не?

7. Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число.

Затем из первого числа вычли второе и получили 1458. Приведите ровно один пример такого числа

В летнем лагере 220 детей и 26 воспитателей. Автобус рассчитан не более чем на 49 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?

2. Тет­радь стоит 24 рубля. Сколь­ко руб­лей за­пла­тит по­ку­па­тель за 60 тет­ра­дей, если при по­куп­ке боль­ше 50 тет­ра­дей ма­га­зин де­ла­ет скид­ку 10% от сто­и­мо­сти всей по­куп­ки?

В таблице даны цены и показатели четырёх моделей электрических мясорубок.

Цена мясорубки (руб. за шт.)

Найдите наивысший рейтинг мясорубки из представленных в таблице моделей.

1) Если в марш­рут­ке есть сво­бод­ные места, то она не тро­га­ет­ся

2) Если марш­рут­ка про­дол­жа­ет сто­ять, то в ней оста­лись сво­бод­ные места

3) Если на каж­дом месте марш­рут­ки сидит пен­си­о­нер, то она тро­га­ет­ся от оста­нов­ки

4) Если марш­рут­ка отъ­е­ха­ла от оста­нов­ки, то в ней за­ня­ты все места

В от­ве­те ука­жи­те но­ме­ра вы­бран­ных утвер­жде­ний без про­бе­лов, за­пя­тых и дру­гих до­пол­ни­тель­ных сим­во­лов.

5. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по логарифмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по логарифмам.

и чётны. В ответе укажите какое-нибудь одно такое число.

7. На поверхности глобуса фломастером проведены 13 параллелей и 25 меридианов. На сколько частей проведённые линии разделили поверхность глобуса?

Меридиан – это дуга окружности, соединяющая Северный и Южный полюсы. Параллель – это окружность, лежащая в плоскости, параллельной плоскости экватора.

1. Павел Иванович купил американский автомобиль, спидометр которого показывает скорость в милях в час. Какова скорость автомобиля в километрах в час, если спидометр показывает 25 миль в час? Считайте, что 1 миля равна 1609 м. Ответ округлите до целого числа.

Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют всеми четырьмя языками: английским, немецким, испанским и французским, а суммарная стоимость их услуг не превышает 12000 рублей в день.

В ответе укажите какой-нибудь один набор номеров переводчиков без пробелов, запятых и других дополнительных символов.

3. Пло­щадь зе­мель фер­мер­ско­го хо­зяй­ства, отведённых под по­сад­ку сель­ско­хо­зяй­ствен­ных куль­тур, со­став­ля­ет 24 га и рас­пре­де­ле­на между зер­но­вы­ми и овощ­ны­ми куль­ту­ра­ми в от­но­ше­нии 5 : 3 со­от­вет­ствен­но. Сколь­ко гек­та­ров за­ни­ма­ют зер­но­вые куль­ту­ры?

4. Со­глас­но рус­ской по­го­вор­ке «Пока гром не гря­нет, мужик не пе­ре­кре­стит­ся», вы­бе­ри­те утвер­жде­ния, ко­то­рые сле­ду­ют из этой по­го­вор­ки.

1) Если гря­нул гром, мужик пе­ре­кре­стит­ся

2) Если мужик не кре­стил­ся, то грома не было

3) Если не было ни грома, ни мол­нии, то мужик не кре­стил­ся

4) Если мужик пе­ре­кре­стил­ся, то был гром

В от­ве­те ука­жи­те но­ме­ра вы­бран­ных утвер­жде­ний без про­бе­лов, за­пя­тых и дру­гих до­пол­ни­тель­ных сим­во­лов.

5. В чемпионате по гимнастике участвуют 70 спортсменок: 25 из США, 17 из Мексики, остальные из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.

6. Вычеркните в числе 23 462 141 три цифры так, чтобы получившееся число

делилось на 12. В ответе укажите ровно одно получившееся число.

Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 12 прыжков, если он начинает прыгать из начала координат?

В летнем лагере на каждого участника полагается 40 г сахара в день. В лагере 161 человек. Сколько килограммовых пачек сахара понадобится на весь лагерь на 9 дней?

В сен­тяб­ре 1 кг ви­но­гра­да стоил 60 руб­лей, в ок­тяб­ре ви­но­град по­до­ро­жал на 25%, а в но­яб­ре еще на 20%. Сколь­ко руб­лей стоил 1 кг ви­но­гра­да после по­до­ро­жа­ния в но­яб­ре?

Каж­дую се­кун­ду бак­те­рия де­лит­ся на две новые бак­те­рии. Из­вест­но, что весь объём од­но­го ста­ка­на бак­те­рии за­пол­ня­ют за 1 час. За сколь­ко се­кунд бак­те­рии за­пол­ня­ют по­ло­ви­ну ста­ка­на?

Среди сотрудников фирмы А некоторые летом 2013 года отдыхали в Греции, а

некоторые — в Испании. Все те сотрудники, которые отдыхали в Испании, не

отдыхали в Греции. Выберите утверждения, которые следуют из приведённых

1) Сотрудник фирмы А, который летом 2013 года не отдыхал в Греции, обязательно

2) Каждый сотрудник фирмы А отдыхал за лето 2013 года хоть где-то.

3) Среди тех сотрудников, которые не отдыхали в Испании летом 2013 года, есть хотя бы

один сотрудник, который отдыхал в Греции.

4) Нет ни одного сотрудника фирмы А, который за лето 2013 года отдыхал и в Греции, и в

Вычеркните в числе 123456 три цифры так, чтобы получившееся число делилось

на 27. в ответе укажите какое-нибудь одно такое число.

На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?

Выпускники 11 «А» покупают букеты цветов для последнего звонка: из 3 роз каждому учителю и из 9 роз классному руководителю и директору. Они собираются подарить букеты 19 учителям (включая директора и классного руководителя), розы покупаются по оптовой цене 30 рублей за штуку. Сколько рублей стоят все розы?

27 вы­пуск­ни­ков школы со­би­ра­ют­ся учить­ся в тех­ни­че­ских вузах. Они со­став­ля­ют 30% от числа вы­пуск­ни­ков. Сколь­ко в школе вы­пуск­ни­ков?

Саша при­гла­сил Петю в гости, ска­зав, что живёт в седь­мом подъ­ез­де в квар­ти­ре № 462, а этаж ска­зать забыл. По­дой­дя к дому, Петя об­на­ру­жил, что дом се­ми­этаж­ный. На каком этаже живёт Саша? (На всех эта­жах число квар­тир оди­на­ко­во, но­ме­ра квар­тир в доме на­чи­на­ют­ся с еди­ни­цы.)

В доме Кости больше этажей, чем в доме Олега, в доме Тани меньше этажей, чем в доме Олега, а в доме Феди больше этажей, чем в Танином доме.

Выберите утверждения, которые следуют из приведённых данных.

1) Дом Тани самый малоэтажный среди перечисленных четырёх.

2) В доме Олега меньше этажей, чем в доме Феди.

3) В Костином доме больше этажей, чем в Танином.

4)Среди этих четырёх домов точно нет двух с одинаковым количеством этажей.

Вычеркните в числе 14563743 три цифры так, чтобы получившееся число делилось на22. в ответе укажите какое-нибудь одно такое число.

Какова вероятность того, что случайно выбранное натуральное число от 52 до 67 делится на 4?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-018411

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

ЕГЭ в 2022 году пройдет в доковидном формате

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

В Москве новогодние каникулы в школах могут начаться с 27 декабря

Время чтения: 1 минута

НИУ ВШЭ откроет первую в России магистратуру по управлению низкоуглеродным развитием

Время чтения: 2 минуты

Росприроднадзор призвал ввести в школах курс по экологии

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник