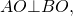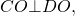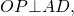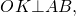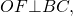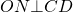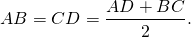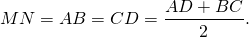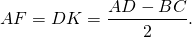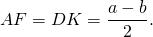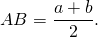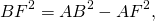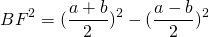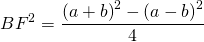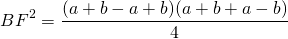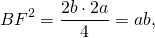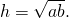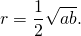Известно что в трапецию можно вписать окружность

Вписанная в трапецию окружность

Когда в трапецию можно вписать окружность? Какими свойствами обладает вписанная в трапецию окружность? Где находится центр этой окружности? Чему равен ее радиус?

1. В трапецию можно вписать окружность тогда и только тогда когда суммы ее противоположных сторон равны.

1) В трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

2) Обратно, если AD+BC=AB+CD, то в трапецию ABCD можно вписать окружность.

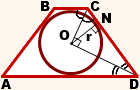
2. Центр вписанной в трапецию окружности — точка пересечения её биссектрис.

O — точка пересечения

биссектрис трапеции ABCD.

3. По свойству биссектрис трапеции, прилежащие к её боковой стороне,

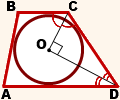
и точка O лежит на средней линии трапеции.

4. Точки касания, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины:

5.

6. Диаметр вписанной в трапецию окружности равен высоте трапеции, радиус — половине высоты:

Источник

Вписанная в равнобедренную трапецию окружность

Какими свойствами обладает вписанная в равнобедренную трапецию окружность?

1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.

То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.

И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.

Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:

2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.

Если MN —

3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.

По свойству равнобедренной трапеции,

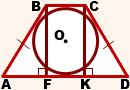
Из прямоугольного треугольника ABF по теореме Пифагора

4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство

5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.

6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.

Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,

Источник

Известно что в трапецию можно вписать окружность

Боковые стороны трапеции, описанной около окружности, равны 11 и 1. Найдите среднюю линию трапеции.

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда

Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда

Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.

В четырехугольник можно вписать окружность тогда и только тогда, когда

Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 42. Найдите радиус окружности.

В четырехугольник можно вписать окружность тогда и только тогда, когда

Около окружности описана трапеция, периметр которой равен 40. Найдите длину её средней линии.

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда

Около окружности описана трапеция, периметр которой равен 84. Найдите длину её средней линии.

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда

Окружность, вписанная в треугольник АВС, площадь которого равна 66, касается средней линии, параллельной стороне ВС. Известно, что ВС = 11. Найдите сторону АВ.

Обозначим AB = x, AC = y, пусть p — полупериметр треугольника ABC. Пусть M и N — середины сторон AB и AC соответственно. Тогда

В трапеции BMNC вписана окружность, поэтому

Отсюда находим, что или

Окружность, вписанная в треугольник ABC, площадь которого равна 114, касается средней линии, параллельной стороне BC. Известно, что BC = 19. Найдите сторону AB.

Обозначим AB = x, AC = y, p — полупериметр треугольника ABC. Пусть M и N — середины сторон AB и AC соответственно. Тогда

В трапецию BMNC вписана окружность поэтому

Отсюда находим, что x = 20 или x = 37.

Аналоги к заданию № 500920: 507598 511448 Все

Окружность, вписанная в треугольник ABC, площадь которого равна 8, касается средней линии, параллельной стороне BC. Известно, что BC = 8. Найдите сторону AB.

Обозначим AB = x, AC = y, p — полупериметр треугольника ABC. Пусть M и N — середины сторон AB и AC соответственно. Тогда

В трапецию BMNC вписана окружность поэтому

Отсюда находим, что или

Ответ:

Аналоги к заданию № 500920: 507598 511448 Все

В окружность радиуса вписана трапеция с основаниями 2 и 4. Найдите расстояние от центра окружности до точки пересечения диагоналей трапеции.

Возможны два случая.

Случай 1. Оба основания трапеции лежат по одну сторону от центра окружности.

Проведем диаметр окружности, перпендикулярный основаниям. Он поделит их пополам. Пусть он пересек основание в точке M и основание в точке N. Обозначим также центр окружности за O, а точку пересечения диагоналей за T. Имеем тогда

Поэтому высота трапеции

Заметим, что треугольники ATD и BTC подобны (по двум углам), причем коэффициент подобия равен поэтому и их высоты из точки T относятся также, откуда Наконец,

Случай 2. Основания трапеции лежат по разные стороны от центра. Тогда все вычисления остаются теми же кроме того, что теперь высота трапеции соответственно то есть точка T лежит с той же стороны от центра, что и меньшее основание трапеции, поэтому

Ответ:

Через вершины А и С прямоугольного треугольника ABC (∠B = 90°) проведена окружность с центром в точке О, касающаяся прямой AB и пересекающая продолжение стороны BC в точке E.

а) Докажите, что сумма углов AOE и AOC равна 180°.

б) Найдите диаметр окружности, если известно, что BE = 5, AC = 6.

а) Из условия задачи следует, что AO ⊥ AB. Следовательно, AO || BE как два перпендикуляра к одной и той же прямой.

Сделаем дополнительное построение: продолжим AO до пересечения с другой точкой окружности, которую обозначим D. Соединим точки E и D отрезком. Мы получили вписанную трапецию ACED, одним основанием которой будет служить диаметр заданной окружности.

Так как в окружность можно вписать только равнобедренную трапецию, то DE = AC = 6. Но эти же равные хорды стягивают и равные дуги АС и DE. Следовательно, равным дугам соответствующие центральные углы AOC и DOE обязаны быть равными.

Отсюда: ∠AOE + ∠AOC = ∠AOE + ∠ DOE = 180°, что и требовалось доказать.

б) Заметим, что ∠AED = 90° как вписанный, опирающийся на диаметр AD. Два прямоугольных треугольника ABE и AED имеют равные острые углы: ∠BEA и ∠EAD (внутренние накрест лежащие при параллельных BE, AD и секущей AE). Следовательно, они (треугольники) подобны, откуда:

В прямоугольном треугольнике AED по теореме Пифагора: AD 2 = AE 2 + DE 2 = 5AD + 36. То есть

;

Дана трапеция ABCD, где AB = BC = CD, точка E лежит на плоскости так, что BE ⊥ AD и CE ⊥ BD

а) Докажите, что углы AEB и BDA равны.

б) Найдите площадь трапеции, если AB = 50, а

а) Докажем, что точка E лежит на окружности, описанной вокруг трапеции ABCD. В самом деле, углы BEC и BDA равны как углы с соответственно перпендикулярными сторонами, а углы BDA и BDC равны как опирающиеся на равные дуги. Следовательно, ∠BEC = ∠BDC, а потому и точки B, E, D, C лежат на одной окружности. Тогда углы BEA и BDA равны как опирающиеся на одну дугу.

Пусть K — точка пересечения AD и BE, тогда из прямоугольного треугольника ABK получаем и

.

Так как трапеция ABCD — равнобедренная, а BK — её высота, средняя линия трапеции равна Окончательно получаем:

Дана трапеция ABCD, где AB = BC = CD, точка E лежит на плоскости так, что BE ⊥ AD и CE ⊥ BD

а) Доказать, что ∠AEB = ∠BDA

б) Найти площадь ABCD, если AB = 72,

а) Докажем, что точка E лежит на окружности, описанной около равнобокой трапеции ABCD. В самом деле, ∠BEC = ∠BDA, как углы с соответственно перпендикулярными сторонами. А ∠BDA = ∠BDC, как опирающиеся на равные дуги. Окончательно получаем, ∠BEC = ∠BDC и точки B, E, D, C лежат на одной окружности. Тогда ∠BEA = ∠BDA, как опирающиеся на одну дугу.

Пусть K — точка пересечения AD и BE, тогда из прямоугольного треугольника ABK получаем и

.

Так как трапеция ABCD — равнобокая и BK — её высота, средняя линия трапеции равна Окончательно получаем:

Ответ:

Аналоги к заданию № 563669: 563670 Все

Две окружности разных радиусов касаются внешним образом в точке K. Прямая касается первой окружности в точке А, а второй окружности в точке В. Луч BK пересекает первую окружность в точке D, луч AK пересекает вторую окружность в точке С.

а) Докажите, что четырёхугольник ABCD — трапеция.

б) Найдите радиус окружности, описанной около треугольника BCD, если радиус первой окружности равен 1, а радиус второй окружности равен 4.

а) Пусть прямая КМ — общая касательная двух окружностей, причём точка M лежит на отрезке AB. Тогда по свойству отрезков касательных, проведённых из одной точки к окружности, Следовательно, точка К лежит на окружности диаметром AB, а значит,

Углы AKD и BKC прямые, поэтому AD и BC — диаметры первой и второй окружностей соответственно. Значит, неравные отрезки AD и BC перпендикулярны касательной АB, следовательно, они параллельны. Таким образом, четырёхугольник ABCD — трапеция.

б) Пусть точки О и Q — центры первой и второй окружностей соответственно, а точки E и H — проекции точек О и D соответственно на прямую BC. Тогда в прямоугольном треугольнике OEQ:

В прямоугольном треугольнике DCH:

В прямоугольном треугольнике BDH:

По теореме синусов радиус окружности, описанной около треугольника BDC, равен

Ответ: б)

Дана трапеция ABCD, основания которой BC = 44, AD = 100, AB = CD = 35. Окружность, касающаяся прямых AD и AC, касается стороны CD в точке K. Найдите длину отрезка CK.

Найдем диагональ AC. Опустим из вершин B и С на сторону AD перпендикуляры BE и СF соответственно. AE = FD, так как трапеция равнобедренная. BCFE — прямоугольник.

Возможны две геометрические конфигурации.

Первый вариант: окружность вписана в треугольник ACD:

Второй вариант: окружность касается продолжения сторон AC и AD за точками C и D соответственно и отрезка CD:

Решение опирается на известную теорему: расстояние от вершины треугольника до точки касания исходящей из этой вершины стороны со вписанной в треугольник окружностью, равно разности полупериметра треугольника и стороны, противолежащей этой вершине.

Но ничего этого в решении нет, кроме того, ADC не прямоугольный, что доказывается по теореме Пифагора.

В чем же секрет вашего решения?

Секрет решения прост.

Отрезки касательных, проведенных из одной точки, равны. Для любого треугольника, в который вписана окружность верно:

Для проверьте сами.

Здравствуйте. Во вто­рой случае, когда мы ищем СК, непонятно, по­че­му СК=. Вы мо­же­те привести доказательство. За­ра­нее спасибо.

Все по той же причине равенства отрезков касательных проведенных из одной точки.

Трапеция ABCD с основаниями AD и BC вписана в окружность с центром O. Найдите высоту трапеции, если её средняя линия равна 3 и

Пусть Изобразим две ситуации: когда угол острый и когда — тупой.

Проведём высоту BH и диагональ Отрезок HD равен средней линии. Из прямоугольного треугольника BHD найдём высоту: Последнее равенство верно, поскольку вписанный угол BDA в два раза меньше центрального угла Воспользуемся формулой тангенса половинного угла:

Если то и

Если то и

Источник