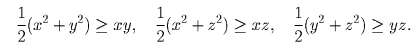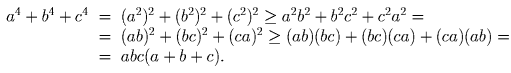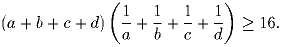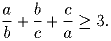Известно что выполнено равенство b 1 3a 1 4x
Известно, что выполнено равенство b = 1 / 3a + 1 / 4x?
Известно, что выполнено равенство b = 1 / 3a + 1 / 4x.
Выразите вектор х через векторы а и b.
Помогите пожалуйста, как можно быстрее!
ПОЖАЛУЙСТА?
Найдите такое число k, что бы выполнялось равенство вектор n = k * вектор m, если известно что : б)векторы m и n сонаправлены и m = 12 см, а n = 240 см.
Даны вектора a и b?
Даны вектора a и b.
Вектор а = √2, вектор в = 6.
Выразите через вектора a и b следующие векторы BM AD AC BD.
Дан параллелограмм ABCD?
Дан параллелограмм ABCD.
Выразите вектор ba через векторы bc и ac.
Выполните сложение векторов ВА и ВС?
Выполните сложение векторов ВА и ВС.
ПОМОГИТЕ ПОЖАЛУЙСТАДан тетраэдр ABCD, K принадлежит BC, CK = KB, вектор AD = вектору а, вектор AB = вектору b, вектор AC = вектору с?
Дан тетраэдр ABCD, K принадлежит BC, CK = KB, вектор AD = вектору а, вектор AB = вектору b, вектор AC = вектору с.
Выразите вектор DK через векторы а, b, с.
Взвешиваем любые два слитка. Если вес равный, то не взвешенный слиток точно весит не 4 грамма. Делаем второе взвешивание со слитком который точно весит не 4 грамма и с любым другим. Если слиток который весит точно не 4 грамма тяжелее, значит он то..
1)а)13, 365 б)1, 6835 2)0, 01.
Ответ на 1) 2700 Ответ на 2) 80.
Конечный ответ 25 процентов, надеюсь по записи разберешься.
24 / 32 = 3 / 4 (24 / 32 = 0. 75 0. 75 * 4 = 3 ).
Ответ : 1440Пошаговое объяснение : На фото.
Известно что выполнено равенство b 1 3a 1 4x
Задача 17:
Докажите, что 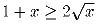
Решение:
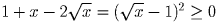
Задача 18:
Докажите, что x + 1/x ≥ 2 при x > 0.
Решение:
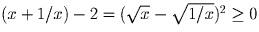
Задача 19:
Докажите, что (x² + y²)/2 ≥ xy при любых x и y.
Решение:
Перегруппировав члены, получаем (x – y)² ≥ 0.
Задача 20:
Докажите, что 2(x² + y²) ≥ (x + y)² при любых x и y.
Решение:
Перегруппировав члены, получаем (x – y)² ≥ 0.
Задача 21:
Докажите, что 1/x + 1/y ≥ 4/(x + y) при x,y > 0.
Решение:
Приводим к общему знаменателю и получаем (x – y)² ≥ 0.
Задача 22:
Докажите, что x² + y² + z² ≥ xy + yz + zx при любых x, y, z.
Решение:
Запишем три неравенства:
Сложив их, мы и получим требуемое неравенство.
Задача 23:
a, b, c ≥ 0. Докажите, что (a + b)(a + c)(b + c) ≥ 8abc.
Решение:
Надо перемножить три неравенства: 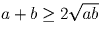
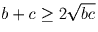
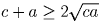
Задача 24:
a, b, c ≥ 0. Докажите, что 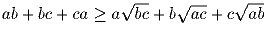
Решение:
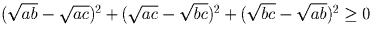
Задача 25:
Докажите, что x² + y² + 1 ≥ xy + x + y при любых x и y.
Решение:
x² + y² + 1 – xy – x – y = ((x – y)² + (x – 1)² + (y – 1)²)/2 ≥ 0.
Задача 26:
Докажите, что при любых a, b, c имеет место неравенство: a 4 + b 4 + c 4 ≥ abc(a + b + c).
Решение:
Воспользуемся неравенством x² + y² + z² ≥ xy + yz + zx, причем дважды:
Задача 27:
Докажите, что x 4 + y 4 + 8 ≥ 8xy при любых x и y.
Решение:
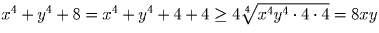
Задача 28:
a, b, c, d – положительные числа. Докажите, что
Решение:
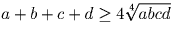
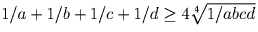
Задача 29:
a, b, c – положительные числа. Докажите, что
Решение:
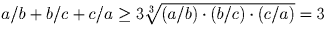
Задача 30:
Докажите, что при x ≥ 0 имеет место неравенство 3x³ – 6x² + 4 ≥ 0.
Решение:
Докажем, что 3x³ + 4 ≥ 6x². Но 3x³ + 4 = 2x³ + x³ + 4. Применяя неравенство Коши, получаем
Задача 31:
Докажите, что при a, b, c > 0 имеет место неравенство 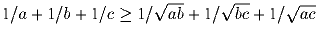
Задача 32:
Докажите, что при a, b, c > 0 имеет место неравенство ab/c + ac/b + bc/a ≥ a + b + c.
Задача 33:
Докажите, что при a, b, c ≥ 0 имеет место неравенство ((a + b + c)/3)² ≥ (ab + bc + ca)/3.
Задача 34:
Докажите, что при a, b, c ≥ 0 имеет место неравенство (ab + bc + ca)² ≥ 3abc(a + b + c).
Задача 35:
Сумма трех положительных чисел равна шести. Докажите, что сумма их квадратов не меньше 12.
Задача 36:
Докажите, что при x ≥ 0 имеет место неравенство 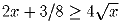
Задача 37:
Сумма двух неотрицательных чисел равна 10. Какое максимальное и какое минимальное значение может принимать сумма их квадратов?
Задача 38:
Докажите неравенство Коши для пяти чисел, т.е. докажите, что при a, b, c, d, e ≥ 0 имеет место неравенство
Решение:
Указание. Докажите сначала неравенство Коши для восьми чисел, а затем воспользуйтесь той же идеей, что и при доказательстве неравенства Коши для трех чисел.