какие колебания называются собственными

Свободные колебания.

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинети­ческой) при отсутствии внешних воздействий.

Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними обра­зуют систему тел, которая называется колебательной системой.

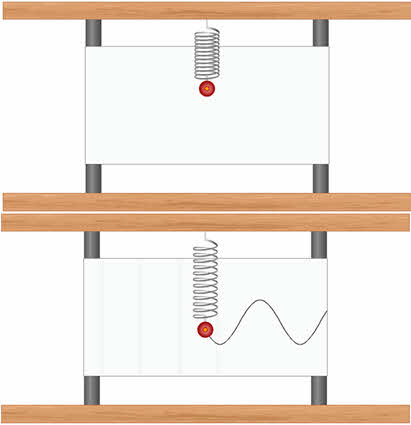
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины (см. рис. ниже), входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.

Другим классическим примером механической колебательной системы является математический маятник (см. рис. ниже). В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия.

Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называют­ся силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свобод­ные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.

Условиями возникновения свободных колебаний являются:

1) возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;

2) отсутствие трения в системе.

Динамика свободных колебаний.

.

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени (ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.

Знак минус появился потому, что сила и угол отклонения от положения равновесия α име­ют противоположные знаки. Для малых углов отклонения sin α ≈ α. В свою очередь, α = s/l, где s — дуга OA, I — длина нити. Учитывая, что а_τ = s», окончательно получим:

.

Вид уравнения аналогичен уравнению . Только здесь параметрами системы являются длина нити и ускорение свободного падения, а не жесткость пружины и масса шарика; роль координаты играет длина дуги (т. е. пройденный путь, как и в первом случае).

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.

Решением уравнений и является функция вида:

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими:

В уравнении x = x_m cos ω₀ t (или x = x_m sin ω₀ t), х_m — амплитуда колебания, ω₀ — собственная циклическая (круговая) частота колебаний.

Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

.

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.

Для математического маятника выполняются равенства:

.

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).

Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.

Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятни­ка, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.

Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции (x = x_m cos ω₀ t (или x = x_m sin ω₀ t)), получим выражение для скорости:

где a_m = ω 2 ₀ x_m — амплитуда ускорения. Таким образом, амплитуда скорости гармонических коле­баний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания.

Источник

Величины, характеризующие КД. Гармонические колебания

Урок 23. Физика 9 класс (ФГОС)

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Величины, характеризующие КД. Гармонические колебания»

На прошлом уроке мы познакомились с новым видом механического движения — колебательным. Давайте вспомним, что это движение, при котором состояния тела с течением времени повторяются, при этом тело проходит через положение устойчивого равновесия поочерёдно в противоположных направлениях. Причём, если колебания происходят в системе только под действием внутренних сил, то такие колебания называются свободными.

А ещё мы дали определение маятника. Напомним, что это твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.

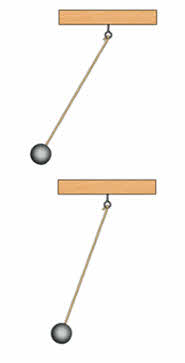
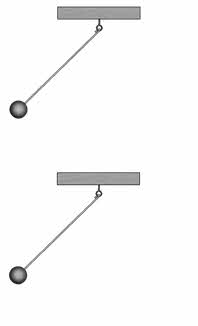
На рисунке вы видите два колеблющихся нитяных маятника. Чем они отличаются?

Правильно, верхний маятник колеблется с большим размахом, чем нижний.

В физике наибольшее по модулю отклонение колеблющегося тела от положения равновесия называют амплитудой колебаний.

Она зависит только от того, на сколько тело было отведено от положения равновесия перед тем, как его предоставили самому себе. Обозначается амплитуда большой буквой А. Единицей её измерения в СИ является метр.

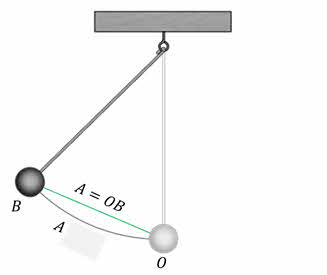
Мы с вами будем изучать колебания, амплитуда которых мала, то есть когда длину дуги ОВ можно считать равной длине отрезка ОВ.

На прошлом уроке мы с вами ввели в рассмотрения величину, называемую периодом колебаний. Напомним, что это промежуток времени, в течение которого тело совершает одно полное колебание. Иными словами, это время, за которое колеблющееся тело проходит путь, равный четырём амплитудам:

По аналогии с вращательным движением, число колебаний в единицу времени называется частотой колебаний. За единицу частоты в СИ принято одно колебание в секунду. Эта единица называется герцем, в честь немецкого учёного Генриха Герца, с трудами которого вы познакомитесь в старших классах.

Как и при движении тела по окружности, период колебаний и частота связаны между собой обратной пропорциональностью.

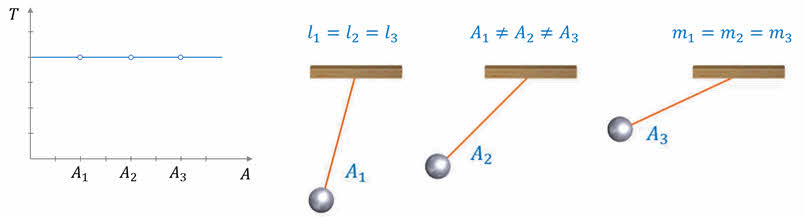
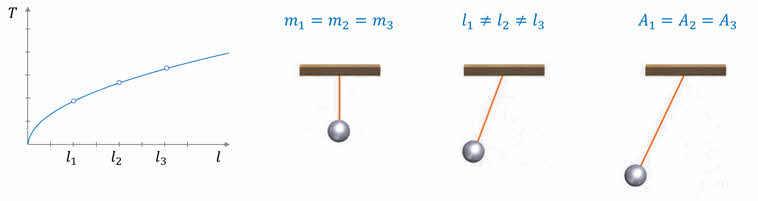
Продолжим рассматривать колебания нитяного маятника. Давайте проведём эксперимент, который покажет, зависит ли его период колебаний от амплитуды? Для этого возьмём три маятника с одинаковыми длинами нитей и грузами одной массы, но запустим каждый маятник с разного расстояния относительно положения равновесия.

Не трудно заметить, что период колебаний нитяного маятника не зависит от амплитуды.

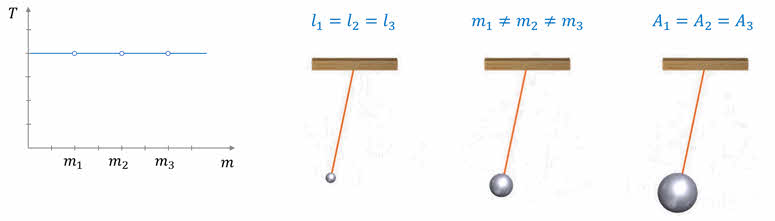
Теперь посмотрим, зависит ли период колебаний от массы маятника. Опять рассмотрим три маятника с одинаковыми длинами нитей, но с разными массами грузов.

Из опыта видно, что все три маятника имеют одинаковые периоды колебаний, то есть период колебаний не зависит от массы груза.

И, наконец, проверим, зависит ли период колебаний маятника от длины его нити. Для этого возьмём три маятника с одинаковыми массами грузов, но с разными длинами нитей.

Колебания маятников наглядно нам демонстрируют, что их период зависит от длины нити маятника: чем длиннее нить, тем больше период колебаний и меньше частота.

Свободные колебания, происходящие при отсутствии трения и сопротивления воздуха, называются собственными колебаниями, а их частота — собственной частотой колебательной системы.

Не только нитяной маятник, но и любая другая колебательная система имеет определённую собственную частоту, которая будет зависеть от параметров колебательной системы.

Например, нетрудно показать, что период колебаний пружинного маятника зависит от массы груза и жёсткости пружины.

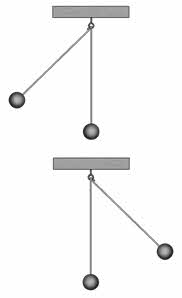
Теперь давайте рассмотрим колебания двух абсолютно одинаковых нитяных маятника. Выведем их из положения равновесия, отклонив верхний маятник на некоторый угол влево, а нижний — на такой же угол, но вправо, и отпустим их. Итак, оба маятника колеблются с одинаковым периодом (так как длины их нитей равны) и с одинаковыми амплитудами. Но в любой момент времени скорости маятников направлены в противоположные стороны. В этом случае говорят, что маятники колеблются в противофазе друг с другом.

Повторим опыт, но теперь отклоним маятники в одну сторону на один и тот же угол. Маятники вновь колеблются с одинаковыми частотами, но теперь их скорости в каждый момент времени направлены одинаково. Говорят, что такие маятники колеблются в одинаковых фазах (или синфазно).

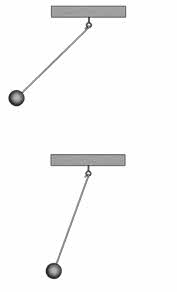
И последний случай. В момент начала наблюдения скорости обоих маятников сонаправлены. Однако через небольшой промежуток времени скорости маятников направлены в противоположные стороны. В таком случае говорят, что колебания маятников происходят с определённой разностью фаз.

Таким образом, фаза колебаний — это физическая величина, которая показывает, на сколько колебания одного маятника отстают или опережают колебания другого маятника. Это определение, конечно, не очень строгое, но для понимания сути величины, вполне достаточное.

Таким образом, любой колебательное движение характеризуется тремя величинами:

· периодом колебаний (или частотой);

Простейшим видом колебательного движения являются гармонические колебания. Термин «гармонические колебания» впервые был введён в науку швейцарским физиком Даниилом Бернулли.

Итак, гармоническими называются такие колебания, которые происходят под действием силы, пропорциональной смещению колеблющегося тела и направленной противоположно этому смещению.

При определённых условиях примером гармонических колебаний будут служить колебания пружинного маятника.

Установим графическую зависимость смещения колеблющегося тела от времени. Для этого проведём такой опыт. Прикрепим к пружинному маятнику грифель от карандаша, а за маятником расположим бумажную ленту и будем равномерно её тянуть. На ленте мы увидим линию, которая по форме будет совпадать с графиком колебаний.

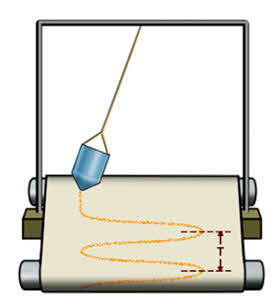
График колебаний математического маятника можно получить, проведя аналогичный опыт. Маятником здесь служит воронка с песком. Если под колеблющимся маятником равномерно тянуть бумажную ленту, перпендикулярно плоскости колебаний, то на ней останется волнообразная дорожка из песка. Каждая точка этой дорожки соответствует положению маятника в тот момент, когда он проходил над ней.

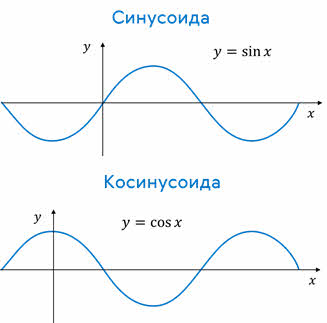
Из результатов двух опытов мы видим, что след, который оставляет песок или карандаш на листе бумаги, есть некая волнообразная кривая. Её называют синусоидой. Из курса математики старших классов вы узнаете, что такие же графики имеют функции типа:

Значит, графически зависимость смещения колеблющейся точки от времени изображается синусоидой или косинусоидой.

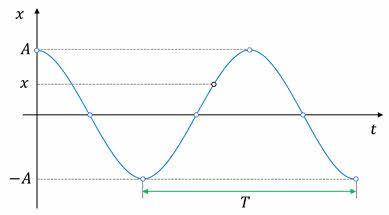
Если провести ось времени через точки, соответствующие положению равновесия маятника, а перпендикулярно ей — ось смещения, то по графику колебаний можно определить все характеристики колебательного движения. Так, максимальные отклонения маятника от положения равновесия в обе стороны одинаковы по модулю и равны А — это амплитуда колебания. А расстояние между двумя пиками графика — период колебаний.

То есть смотрите, маятник начал движение из крайней точки с координатой А. Затем, пройдя положение равновесия, дошёл до второй крайней точки с координатой –А, на мгновение остановился в ней, поменяв направление скорости на противоположное, а затем продолжил движение в обратном направлении и, вновь пройдя через положение равновесия, вернулся туда, откуда начал движение. Затем движение маятника повторяется.

Так же с помощью данного графика можно примерно определить координату маятника в любой момент времени.

Теперь мы можем дать более строгое определение гармонических колебаний. Итак, гармоническими колебаниями называются периодические изменения во времени физической величины, происходящие по закону синуса или косинуса.

Рассмотренные нами колебания нитяного маятника близки к гармоническим, но не являются таковыми, из-за действия различных сил сопротивления. Но если бы маятник представлял собой материальную точку, колеблющуюся без трения с малой амплитудой при неизменном расстоянии от неё до точки подвеса, то его колебания были бы строго гармоническими. Такая колебательная система называется математическим маятником.

Следует помнить, что при совершении телом гармонических колебаний не только его координата, но и такие величины, как сила, ускорение и скорость тоже изменяются по закону синуса или косинуса. Это следует из известных вам законов и формул, в которых указанные величины попарно связаны прямо пропорциональной зависимостью. Из этих формул видно, что сила и ускорение достигают наибольших значений, когда колеблющееся тело находится в крайних положениях, где смещение наиболее велико, и равны нулю, когда тело проходит через положение равновесия.

Что же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия достигает наибольшего значения.

Источник

СОБСТВЕННЫЕ КОЛЕБАНИЯ

Смотреть что такое «СОБСТВЕННЫЕ КОЛЕБАНИЯ» в других словарях:

Собственные колебания — (свободные колебания), колебания, которые совершаются за счет энергии, сообщенной системе в начале колебательного движения (например, в механической системе через начальное смещение тела или придание ему начальной скорости, а в электрической… … Иллюстрированный энциклопедический словарь

СОБСТВЕННЫЕ КОЛЕБАНИЯ — (свободные колебания) колебания, которые могут возбуждаться в колебательной системе под действием начального толчка. Форма и частота собственных колебаний определяются массой и упругостью для механических собственных колебаний и индуктивностью и… … Большой Энциклопедический словарь

СОБСТВЕННЫЕ КОЛЕБАНИЯ — (Oscillations) свободные колебания тела или колебательного контура по инерции, когда на них не действует периодическая внешняя сила. С. К. имеют вполне определенный период (собственный период); напр. колебания корабля после того, как его… … Морской словарь

собственные колебания — Свободные колебания по одной из собственных форм. [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики строительная механика, сопротивление материалов EN … Справочник технического переводчика

собственные колебания — (свободные колебания), колебания, которые могут возбуждаться в колебательной системе под действием начального толчка. Форма и частота механических собственных колебаний определяются массой и упругостью, а электромагнитных индуктивностью и… … Энциклопедический словарь

собственные колебания — savieji virpesiai statusas T sritis fizika atitikmenys: angl. eigen oscillations; natural oscillations; self oscillations vok. Eigenschwingungen, f rus. собственные колебания, n pranc. oscillations propres, f … Fizikos terminų žodynas

СОБСТВЕННЫЕ КОЛЕБАНИЯ — свободные колебания, колебания, совершающиеся в динамич. системе при отсутствии внешнего воздействия при сообщении ей в начальный момент внешнего возмущения, выводящего систему из состояния равновесия. Характер С. к. в основном определяется… … Математическая энциклопедия

собственные колебания — ▲ физические колебания ↑ независимый собственные [свободные] колебания возникают под действием начального толчка. автоколебания. самовозбуждение самопроизвольное возникновение колебаний в системе под влиянием внешних воздействий. спектр. триплет … Идеографический словарь русского языка

Собственные колебания — свободные колебания, колебания в механической, электрической или какой либо другой физической системе, совершающиеся при отсутствии внешнего воздействия за счёт первоначально накопленной энергии (вследствие наличия начального смещения или … Большая советская энциклопедия

Источник

Какие колебания называются собственными

Общие понятия теории собственных колебаний.

Собственными называются колебания, которые совершает система около положения устойчивого равновесия после первоначального возмущения под действием только внутренних сил.

Какая сила должна действовать на систему, чтобы колебания были гармоническими? Так как для гармонических колебаний уравнение, связывающее ускорение и координату материальной точки выглядят как

то согласно II закону Ньютона справедливо следующее равенство:

Итак, тело совершает гармонические колебания, если сила, возвращающая его в положение равновесия, пропорциональна смещению и направлена в противоположную этому смещению сторону.
Такая сила называется квазиупругой.

На практике зависимость F(x) является более сложной. Однако, при малых значениях величины х эту функцию можно разложить в ряд:

и пренебречь слагаемыми более высокого, чем 1 порядка малости. Следовательно, любая система с одной степенью свободы при достаточно малом отклонении от положения равновесия будет гармонически колебаться.

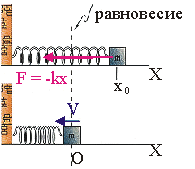
Рис. 10.1.

Значение w₀ зависит только от физических свойств системы и не зависит от начальных условий.

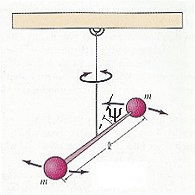
Рис. 10.2. Крутильные колебания.

Сравнивая уравнения (10.6) и (10.1), видим, что они аналогичны. Следовательно, решение уравнения (10.6) имеет вид гармонической функции:

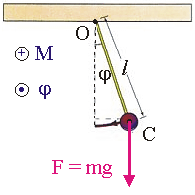
Рис. 10.3. Колебания физического маятника.

Решение этого уравнения имеет следующий вид:

Для математического маятника момент инерции и значение собственной частоты колебаний будут равны:

Собственную частоту физического маятника можно представить в виде, аналогичном выражению для математического маятника:

Собственные затухающие колебания. Логарифмический декремент затухания.

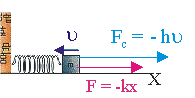
Рис. 10.4.

Уравнение динамики затухающих колебаний. В реальных случаях на тело, совершающее собственные гармонические колебания, действует сила трения. Наиболее распространен случай жидкого трения, когда сила трения (сопротивления среды) пропорциональна скорости:

Уравнение (10.7) справедливо для малых скоростей. Согласно II закону Ньютона уравнение движения тела будет иметь вид:

После несложных преобразований получим:

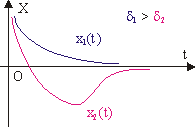
Рис. 10.6. Затухающие колебания в случае большого трения.

и определяется характеристиками колеблющейся системы и окружающей среды. Таким образом, трение уменьшает частоту колебаний. Качественно этот факт можно объяснить так. Сила трения действует против скорости. Следовательно, для линейного осциллятора ее действие эквивалентно уменьшению возвращающей силы, т.е. упругости пружины. Это означает, что частота колебаний w уменьшается, а период Т увеличивается.

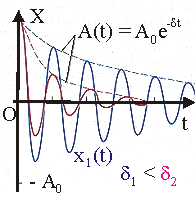
Рис. 10.5. Затухающие колебания.

При большом трении тело колебаний как таковых не совершает (см. рис. 10.6, кривая x₁(t) ). Решение будет иметь вид:

Возможен и промежуточный вариант, также характерный для больших значений коэффициента затухания (кривая x₂(t) на рис. 10.6).

величина 1/ d , равна промежутку времени, по истечении которого амплитуда колебаний уменьшается в е = 2.73 раз.

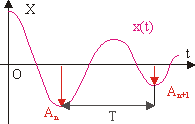
Рис. 10.7. К определению логарифмического декремента затухания.

называется логарифмическим декрементом затухания. Выясним связь между d и d :

Используя уравнение (10.13), можно преобразовать закон изменения амплитуды:

Величина 1/d равна числу колебаний, за которое их амплитуда уменьшается в е раз.

Если значение d невелико ( d ), то можно показать, что

Динамика вынужденных колебаний. Резонанс.

Уравнение динамики колебаний, происходящих под действием гармонической силы. Вынужденными называются колебания, которые система совершает под действием внешней силы. Характер движения зависит от особенностей внешней силы. Она может быть любой периодически изменяющей свое значение. Наиболее важным является случай гармонической внешней силы. Более сложные случаи ее изменения во времени сводятся к этому простейшему.

Будем считать, что внешняя сила действует на линейный гармонический осциллятор по следующему закону:

Кроме внешней силы на осциллятор, по-прежнему, действуют квазиупругая сила и сила трения. Согласно II закону Ньютона уравнение движения имеет вид:

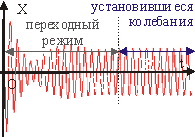
Рис. 10.8.

Таким образом, общее решение будут иметь вид:

Первое слагаемое правой части этого выражения описывает собственные затухающие колебания, зависящие от начальных условий. Из уравнения (10.18) следует, что в течение определенного промежутка времени осциллятор будет совершать сложное негармоническое движение, т.к. оно является результатом сложения двух асинхронных колебаний. Однако, через промежуток времени t

1/ d амплитуда и энергия собственных колебаний уменьшатся до нуля и они прекратятся. При этом второе слагаемое останется неизменным и результирующее колебание будет гармоническим (см. рис. 10.8, 10.9).

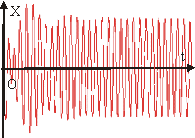
Рис. 10.9.

Переходной и установившийся режимы колебаний. Колебания, которые будут совершаться после затухания собственных колебаний, называются установившимися вынужденными колебаниями. Процесс установления этих колебаний называется переходным режимом (см. рис. 10.8).

Установившиеся колебания не зависят от начальных условий и описываются уравнением:

Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы и существенно зависит от соотношения между частотой вынуждающей силы и собственной частотой.

Величину сдвига фаз между смещением и вынуждающей силой будет равна:

Обратите внимание, что смещение отстает по фазе от вынуждающей силы.

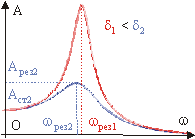
Рис. 10.10. Амплитудно-резонансная кривая.

Из графика видно, что при определенном значении частоты вынуждающей силы амплитуда осциллятора становится максимальной.

Явление, при котором амплитуда колебаний системы достигает максимального значения, характерного для некоторого значении частоты вынуждающей силы называется резонансом.

Частота вынуждающей силы, при которой наступает данное явление, называется резонансной. Приравнивая к нулю производную по частоте выражения (10.20) и пренебрегая слагаемыми второго порядка малости, получим формулы для расчета резонансной частоты w _рез и амплитуды А_рез :

При значении d = 0 амплитуда колебаний в резонансе стремится к бесконечности.

Важной характеристикой осциллятора является отношение амплитуды его колебаний в резонансе к ее статическому значению. Из формул (10.21) и (10.23) следует, что это отношение равно добротности системы:

Добротность является важнейшей характеристикой резонансных свойств системы.

Рассмотрим чему равен сдвиг фаз между смещением и силой при резонансе. Допустим, что при w = w ₀ сила и смещение подчиняются следующим законам:

Тогда уравнение для скорости колеблющейся частицы (осциллятора) имеет вид:

Из этих соотношений видно, что скорость u и сила колеблются в фазе. Следовательно, мощность, сообщаемая осциллятору внешней силой, равна N = F· u. Ее значение положительно в любой момент времени, следовательно, работа внешней силы достигает своего максимального значения. Энергия, передаваемая осциллятору внешней силой, в этом случае направлена на преодоление сил трения.

Примеры . Явление резонанса используется в работе резонансных контуров в электрических схемах, усиливающих полезный сигнал, наличие резонанса необходимо учитывать при расчете механических конструкций на прочность.

Источник