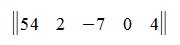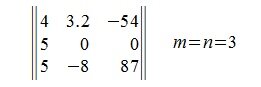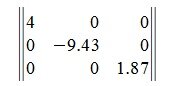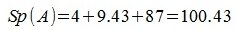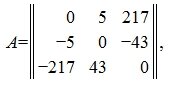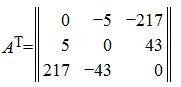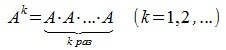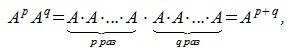какие компоненты входят в состав матрицы

Технология переработки полимерных композиционных материалов

Матричные материалы

1. Матрицы для полимерных композиционных материалов

Понятие «матрица» характеризует непрерывную пространственную фазу, ответственную за сохранение конфигурации изделия, передачу эксплуатационных нагрузок на арматуру, сопротивление действию других внешних факторов.

Разработка полимерных матриц для ПКМ – серьезная и важная проблема, поскольку многие свойства композита определяются структурой матрицы.

Требования к матрицам можно разделить на 3 группы:

1. прочность, жесткость, теплостойкость полимерной матрицы,

2. пластичность, трещиностойкость, ударную вязкость;

3. перерабатываемость, технологичность связующего.

Задача исследователя, конструирующего композиционный материал, – найти компромисс, оптимизировать выбор связующего, учитывая еще экологические, экономические, соображения.

Можно выделить следующие типы матриц:

— металлические (алюминий и сплавы, магниевые сплавы, титан и его сплавы, медь, сплавы никеля и кобальта);

(термопласты: полиэтилен, полипропилен, полистирол, поливинилхлорид, полиамиды и др;

реактопласты: эпоксидные, полиуретановые смолы;

эластомеры: изопреновые каучуки, бутадиеновые, бутадиен-стирольные каучуки;

— керамические (обычная керамика: силикаты;

— керметы, соединения содержащие керамическую Al₂O₃ и металлическую составляющие

Полимерную матрицу для композиционных материалов выбирают, учитывая условия эксплуатации изделий. От материала матрицы значительно зависят свойства композита: прочность, тепло- и влагостойкость, стойкость к действию агрессивных сред, метод получения изделия.

Полимеры в качестве матрицы используют либо в чистом виде (порошки, гранулы, листы, пленки), либо в виде связующих. Связующее представляет собой двух- или многокомпонентную систему из синтетического полимера и отвердителей, инициаторов или катализаторов, ускорителей отверждения. В связующее с целью придания необходимых технологических и эксплуатационных свойств могут быть добавлены растворители, красители, пластификаторы, стабилизаторы и другие компоненты.

При производстве армированных пластиков наиболее часто применяют термореактивные связующие, при нагревании которых происходят необратимые структурные и химические превращения; непрерывно расширяется использование термопластичных полимеров и эластомеров.

Источник

7. Матричные материалы.

В композитах важным элементом является матрица, которая:

1) обеспечивает монолитность композита;

2) фиксирует форму изделия;

3) фиксирует взаимное расположение армирующих волокон;

4) распределяет действующее напряжение по объему материала, обеспечивая равномерную нагрузку на волокна и ее перераспределение при разрушении части волокон;

5) определяют метод изготовления изделий из композитов;

6) определяет возможность выполнения конструкции заданных габаритов;

7) определяет параметры технологических процессов и т. д.

Таким образом, требования, предъявляемые к матрицам, можно разделить на эксплуатационные и технологические.

Эксплуатационные требования. К ним относятся требования, связанные с механическими и физико-химическими свойствами материала матрицы. Они обеспечивают работоспособность композиции при действии различных эксплуатационных факторов:

1. Механические свойства матрицы должны обеспечивать совместную работу армирующих волокон или частиц при различных видах нагрузок.

2. Прочностные характеристики материала матрицы являются определяющими при сдвиговых нагрузках, нагружении композита в направлениях, отличных от ориентации волокон, а также при циклическом нагружении.

3. Природа матрицы определяет уровень рабочих температур композита, характер изменения свойств при воздействии атмосферных и других факторов. С повышением температуры прочность и другие характеристики матричных материалов так же, как и прочность их соединений со многими типами волокон, снижается. Материал матрицы также характеризует устойчивость композита к воздействию внешней среды, химическую стойкость, частично теплофизические, электрические и другие свойства.

Технологические требования к матрице определяются протекающими обычно одновременно процессами получения композита и изделия из него, т. е. процессами совмещения армирующих волокон с матрицей и окончательного формообразования изделия. Целью технологических операций является:

1) обеспечение равномерного (без касания между собой) распределения волокон в матрице при заданном их объемном содержании;

2) максимально возможное сохранение прочностных свойств волокон;

3) создание достаточно прочного взаимодействия на границе волокно – матрица.

Рис. 9. Пространственные схемы армирования

Таким образом, к материалу матрицы предъявляют следующие требования:

1) хорошая смачиваемость волокна;

2) возможность предварительного изготовления полуфабрикатов (например, препрегов) с последующим изготовлением из них изделий;

3) качественное соединение нескольких слоев композитов в процессе формования;

4) невысокие значения параметров формообразования (например, температуры, давления и т. п.).

Для литейного производства применяются следующие матричные материалы: Al, Cu, Fe, Mg, Ni и др., а также промышленные сплавы на их основе.

8.Основные определения и классификация композиционных материалов.

Компоненты в КМ объединены в монолитную единую структуру с границей раздела между структурными составляющими (компонентами), оптимальное сочетание которых позволяет получить комплекс физико-химических и механических свойств, отличающихся от комплекса свойств компонентов.

Компонент, непрерывный во всем объеме композиционного материала, называется матрицей.

Компонент или компоненты прерывистые, разъединенные матрицей, называются арматурой, или армирующим компонентом, или, иногда, наполнителем. Понятие «армирующий» означает «введенный в материал с целью изменения его свойств», но не несет в себе однозначного понятия «упрочняющий».

Композиционный материал классифицируется по нескольким основным признакам:

— материалу матрицы и армирующих компонентов;

— структуре: геометрии (морфологии) и расположению компонентов (структурных составляющих);

Источник

Матрицы. Виды матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

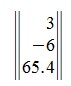
Матрица столбец

Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

Нулевая матрица

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

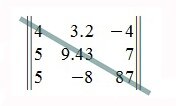
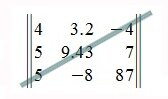
Главная диагональ матрицы

Побочная диагональ матрицы

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

Единичная матрица

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

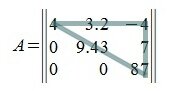
Верхняя треугольная матрица

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

где E-единичная матрица.

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

Источник

От действий над матрицами к пониманию их сути…

Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья «Математика на пальцах», и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.

Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше.

Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.

Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что «площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма». Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.

Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.

Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…

Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.

Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?

Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…

Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.

В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.

Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».

Источник

Матрицы: определение и основные понятия.

Определение матрицы

Количество строк и столбцов задают размеры матрицы.

Обозначение

A =		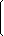4	1	-7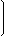
		-1	0	2

Элементы матрицы

Элементы матрицы A_4×4:

A =		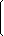4	1	-7	2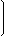
		-1	0	2	44
		4	6	7	9
		11	3	1	5

Демонстрация нулевых и ненулевых строк матрицы:

Демонстрация нулевых и ненулевых столбцов матрицы:

4

1

-7

не не нулевой столбец

Диагонали матрицы

Демонстрация главной и побочной диагонали матрицы:

Источник

• ← какие компоненты входят в состав лакокрасочных материалов
• какие компоненты входят в состав методической системы →

	0	1	-7
	0	0	2