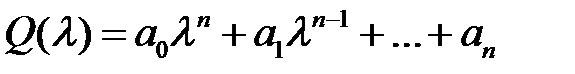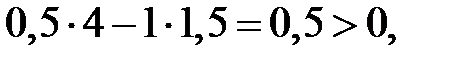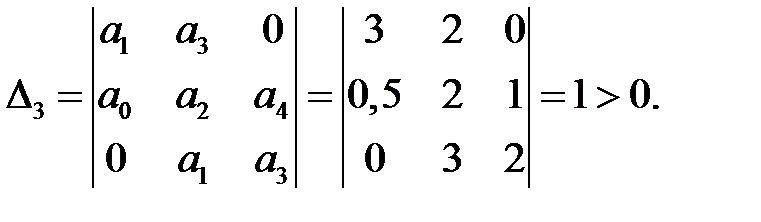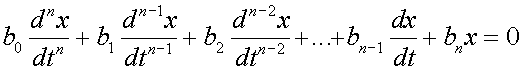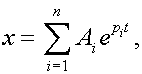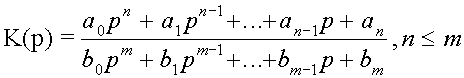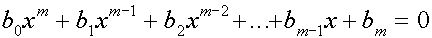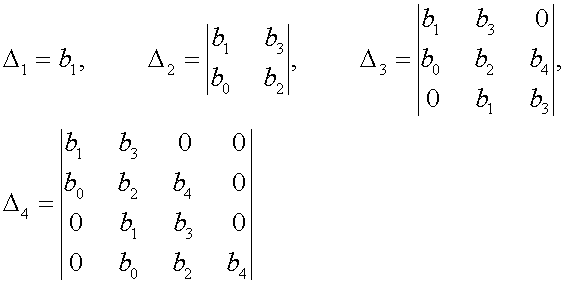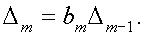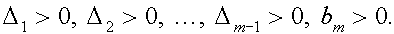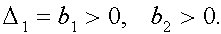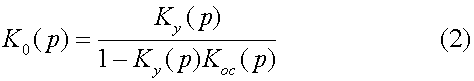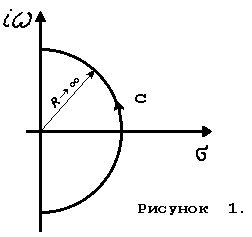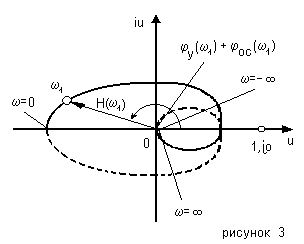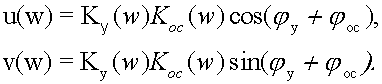какие критерии устойчивости для исследования линейных систем называются алгебраическими

Алгебраические критерии устойчивости. Определение и условия устойчивости

Определение и условия устойчивости.

Еслина систему управления действует двавнешних воздейст­вия — задающее воздействие g, — то в общем случае она описывается уравнением

Основное условие устойчивости. Для того чтобы сис­тема управления была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательную вещественную часть.

На комплексной плоскости корни, имеющие отрицательную ве­щественную часть, располагаются в левой полуплоскости и поэтому называются левыми; корни, имеющие положительную вещественную часть, располагаются в правой полуплоскости и называются правыми; а корни, расположенные на мнимой оси, называются нейтральными.

Таким образом, основное условие устойчивости можно также сфор­мулировать следующим образом: для того чтобы система была устойчива, необходимо и достаточно, чтобы все корни характе­ристического уравнения (нули характеристического полинома) были левыми.

Согласно основному условию устойчивости определение устойчи­вости сводится к исследованию корней характеристического уравне­ния. Однако для этого нет необходимости вычислять эти корни. Существуют различные критерии устойчивости, которые позволяют судить о том, находятся ли корни полинома в левой полуплоскости, не вычисляя их.

Необходимое условие устойчивости.Для того чтобы
система была устойчива, необходимо, чтобы все коэффициенты ее
характеристического уравнения были строго одного знака:

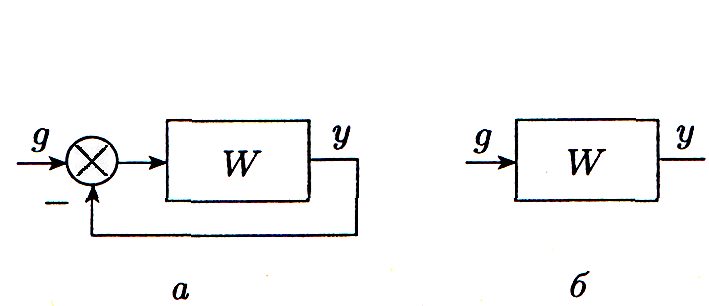
При исследовании замкнутой системы (рис. 1а) нет необходи­мости находить ее передаточную функцию, если известна передаточная функция W(p) = R(p)/S(p) разомкнутой системы (рис. 1б). Ее собственный оператор Q(p) равен сумме полиномов числителя и зна­менателя передаточной функции разомкнутой системы:

Критерий Гурвица.Из коэффициентов характеристичес­кого полинома

составляется определитель n-го порядка который строится следующим образом:

,

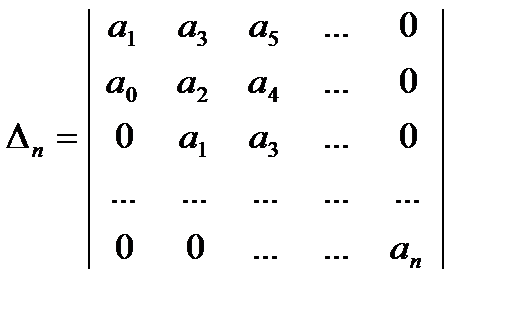
На главной диагонали выпи­сываются элементы a₁,a₂. ,а_п. Затем при движении от этих эле­ментов вверх размещаются коэффициенты в порядке возрастания ин­дексов, при движении вниз — в порядке убывания. Например, при построении i-го столбца, двигаясь от элемента а_i вверх, записыва­ют коэффициенты а_i+1,a_i+2, …, двигаясь вниз, записывают коэффи­циенты a_i-1, a_i-2, … При этом, если индекс превышает п или при­нимает отрицательное значение, соответствующий коэффициент принимают равным нулю.

Главные миноры определителя ∆_п

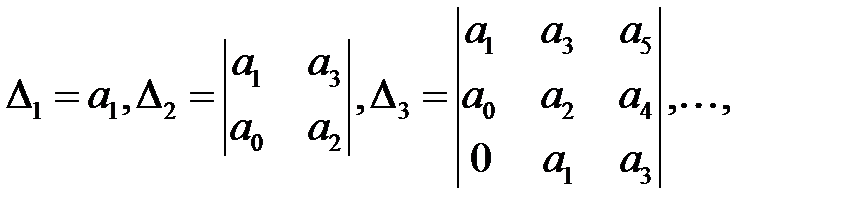
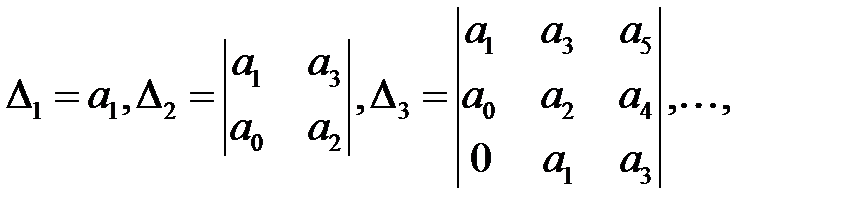
включая сам определитель ∆ называют определителями Гурвица.

Критерий Гурвица (Hurwitz, 1895). Для того чтобы систе­ма была устойчива, необходимо и достаточно, чтобы определители Гурвица, составленные из коэффициентов ее характеристического уравнения, при а₀> 0 были больше нуля:

Критерий Льенара-Шипара.Как отмечалось выше, при исследовании устойчивости с помощью алгебраических крите­риев нужно прежде всего проверить необходимое условие устойчивости. Если необходимое условие устойчивости выполняется, то ока­зывается, что для определения устойчивости, нет необходимости вычислять все определители Гурвица.

Для уменьшения вычислений целесообразно при нечетном п ис­пользовать условие (4), а при четном п — условие (5)

Здесь приведена несколько упрощенная формулировка критерия Льенара-Шипара. При выполнении одного из условий (4) или (5) не все неравенства в необходимом условии устойчивости оказывают­ся независимыми. Поэтому часть неравенств можно опустить. Но так как проверка необходимого условия устойчивости не связана с вычис­лением, на этом мы останавливаться не будем.

Выпишем необходимые и достаточные условия устойчивости для п = 1,2, 3. Из критерия Льенара-Шипара получаем:

Отсюда следует, что при п = 1 и п = 2 необходимое условие устойчивости является и достаточным. Однако уже при п = 3 для устойчивости, кроме выполнения необходимого условия устойчивос­ти, нужно, чтобы была положительной разность между произведения­ми средних и крайних коэффициентов.

Пример 1. Передаточная функция разомкнутой системы

; к = 0,5; к = 2.

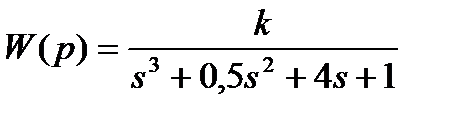
Исследовать устойчивость разомкнутой и замкнутой систем.

Решение. Характеристический полином разомкнутой системы λ 3 +0,5λ 2 +4λ+1. Все коэффициенты больше нуля и определи­тель

∆₂=0,5•4-1• 1=1>0. Поэтому разомкнутая система ус­тойчива.

Характеристический полином замкнутой системы

Q(λ) = λ 3 + 0,5λ 2 +4λ+ l + k

Все коэффициенты этого полинома при обоих значениях к положи­тельны, а определитель ∆₂ при к = 0,5 равен

а при к = 2

∆₂ =0,5*4-1*3=-1 3 + λ 2 + λ. Его коэффициенты a₀=1, a₁=1, а₂=1 и а₃=0. Необходимое условие устойчивости не выполняется, и поэтому разо­мкнутая система неустойчива.

Характеристический полином замкнутой системы

Q(λ) = λ 3 + λ 2 + λ + к.

Все коэффициенты при обоих значениях к положительны, определи­тель ∆₂ при к = 0,5 равен

Решение. В данном случае п = 4 — четное число. Необходимое условие устойчивости выполняется: все коэффициенты а₀ = 0,5, a₁ = 3, а₂ = 2, а₃ = 2, а₄ = 1 положительны. В соответствии с условием (5) достаточно вычислить определитель ∆₃:

Пример 4. Изображение дифференциального уравнения системы имеет вид

Параметры имеют значения: Т₀ = 0,02 сек, T₁ = 0,01 сек, Т₂ = 0,05 сек, k₀= 20, kp = 0,2. Оценить устойчивость системы.

Решение. В соответствии с дифференциальным урав­нением запишем характеристическое уравнение в виде

Применяя критерий устойчивости Льенара-Шипара, имеем при всех положительных коэффициентах следующие соотношения:

Отсюда следует, что

то есть, система устойчива.

Пример 5. Дано характеристическое уравнение автоматической системы четвертого порядка

Коэффициенты уравнения имеют значения:

Определить устойчивость системы.

Решение. Применяя критерий устойчивости Гурвица, проверим, будут ли положительными определители матрицы из коэффициентов характеристического уравнения

Вычисляя определители, получаем:

=

=

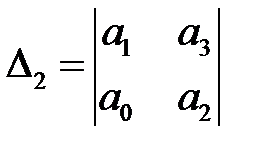
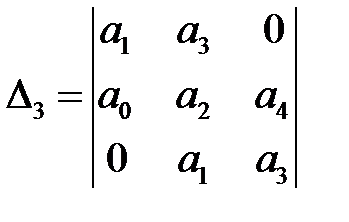
Поэтому для системы четвертого порядка проверка положительности ∆2 является излишней. Также является излишней проверка положительности последнего ∆_n определи­теля для системы любого порядка, так как ∆_n = а_n ∆_n-1 и при a_n > 0 достаточно проверить положительность всех опре­делителей до ∆_n-1.

Поэтому при положительных коэффици­ентах характеристического уравнения для системы четвертого порядка достаточно проверить выполнение неравенства

Для системы пятого порядка при положительных коэф­фициентах необходимо выполнение двух неравенств:

Источник

9. Устойчивость систем управления. Алгебраические критерии устойчивости.

Устойчивость – свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия. Это свойство затухания переходного процесса с течением времени.

Для тех объектов, которые работают в условиях непрерывно меняющихся воздействий, т.е. когда установившийся режим вообще отсутствует, дается общее определение устойчивости:

Система устойчива, если её выходная величина остаётся ограниченной в условиях действия на систему ограниченных по величине возмущений.

Если хотя бы один вещественный корень λ_i будет положительным или хотя бы одна пара комплексно-сопряженных корней будет иметь положительную вещественную часть, то в этом случае процесс будет расходящийся.

Алгебраические критерии. Вычисление корней уравнений высоких степеней затруднительно, поэтому в ТАУ были разработаны косвенные методы, позволяющие судить об устойчивости системы, не находя корней характеристического уравнения. Эти косвенные методы получили название алгебраических критериев. Из алгебраических критериев в ТАУ получили распространение 2 критерия: критерий Раусса, критерий Гурвица.

Критерий Раусса—Гурвица позволяет определять устойчивость системы по коэффициентам хар. урав-ия.

Необходимым условием устойчивости явл.

положительность всех коэф. хар. ур-ия.

Положительности коэффициентов характ. уравнения в общем случае недостаточно для устойчивости системы. Только в частных случаях, когда уравнение 1-ой или 2-ой степени, положительность коэф-тов явл. необходимым и достаточным условием устойчивости.

Чтобы сформулировать критерий Гурвица необходимо составить определитель вида:

— определитель Гурвица

Для устойчивости линейной системы необходимо и достаточно, чтобы были положительными n-главных определителей Гурвица (диагональные миноры). Δ_n = a_n*Δ_n-1 (a_n >0, Δ_n-1 >0)

Δ₁=a₁

Критерий Раусса-Гурвица применяется для систем не выше 4-го порядка. Критерий применяется для анализа систем, у которых известны все коэффициенты характеристического уравнения.

10. Качество установившихся процессов в линейных сау. Коэффициенты ошибок.

Одного фактора устойчивости для нормального функционирования СУ недостаточно. При устойчивой САУ важно также как она выполняет свое функциональное назначение. Требования к системам управления могут быть различными. Это может быть быстродействие системы, энергопотребление, уровень шума и т.д. Совокупность требований, определяющих поведение САУ в установившихся и переходных процессах объединяется понятием качества процесса управления. Качество имеет смысл только для устойчивых САУ. Качество оценивается при наиболее часто встречающихся или наиболее тяжелых для данной системы типовых воздействий.

f (t) = δ(t) – единичный импульс.

f (t) = 1(t) – единичный скачок.

f (t) = const – постоянные воздействия.

5. f(t) = υt – сигнал, изменяющийся с постоянной скоростью.

6. f(t) = a*t 2 /2 – сигнал, изменяющийся с постоянным ускорением.

Качество процесса управления можно рассматривать раздельно для установившихся процессов и для переходных процессов.

Качество установившихся режимов работы САУ.

Главным показателем является точность. Точность оценивается величиной ошибки.

Р/м статический режим. Он характериз. тем, что и задающее и возмущающее воздействие явл. постоянными величинами. Такой режим характерен для статических систем. Р/м структуру:

Для статики, когда S=0 → F(0)=f_ст, Y(0)=y_ст

y_ст = Ф_в(0)* f_ст =.

Статический режим имеет место только в статических САУ.

W(0)=k y_ст=k_0* f_ст – в разомкнутом состоянии. — в замкнутом состоянии.

Замыкание системы создает знаменатель и отклонение y под действием f в (1+k) раз меньше, чем в разомкнутой системе. y_ст –статическая ошибка. Мерой статической точности САУ явл. статизм δ.

График изменения статической ошибки от возмущающего воздействия. Δ нельзя уменьшить за счет коэффициента k_0. В САУ статич.

ошибка измен. за счет общего коэф-та передачи k. В статич. САУ по принципу действия стат. ошибка не может = 0.

Способы устранения статической ошибки.

Увеличение коэф-та передачи системы. Оно не может осущ. не ограниченно, т.к. это ведет к потере уст-ти системы.

Передаточная ф-ия по каналу возмущения =0.

Ф_f(0) =(Знаменатель приравниваем к ∞, или чиcлитель приравниваем к 0).

При реализ-ии управления по возмущению, возмущение в системе прикладывается по 2 каналам:

W_к(S) – передат. ф-ия управления по возмущению.

«-» означает, что корректирующую связь мы должны заводить с обратным знаком по возмущающему воздействию.

Такой способ устранения статической ошибки устраняет только ту статическую ошибку, возмущение по которой можно проконтролировать.

2-ой путь компенсации статической ошибки – введение астатизма. Астатической наз. САУ, структурные схемы которых, будучи приведенные к одноконтурным, содержат хотя бы одно интегрирующее звено (астатическое). У интегрир. звеньев характеристики астатические. Закон регулирования в астатич. САУ интегральный, т.е. выход. сигнал регулятора пропорц. интегралу от ошибки. Если вне объекта имеется хотя бы одно интегрирующее звено, то статич. ошибка, вызванная любой причиной, по принципу действия такой САУ=0.Интегрирующее звено будет изменять управляющее воздействие на объект до тех пор, пока на входе интегрир. звена сигнал не будет = 0, т.е. пока ошибка не станет = 0.

Постоянные ошибки. Среди типовых режимов работы САУ простейшим явл. режим работы при постоянной величине внеш. воздействия (задающего, возмущающего).

G(t) = const W(S) = , свободный член = 1

Ф_ε(S) = (1)

Диф. ур-ие в операторной форме:

Е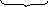сли к записи (2) применить теорему о конечном значении,то ε_уст = lim ε(t) =lim Ф_ε(S)*X(S)*S (3) X(S)=X₀/S X₀

Пользуясь (3) с учетом (1) запишем: ε_уст = X₀/(1+k), если L(S) и N(S) имеют свобод. член = 1.

Источник

Критерии устойчивости линейных систем

Критерии устойчивости линейных систем

Устойчивость линейных систем

В реальной цепи, охваченной обратной связью, всегда имеются реактивные элементы, накапливающие энергию. Даже в усилителе на резисторах имеются такие элементы в виде паразитных емкостей схемы и электронных приборов, переходные конденсаторы, индуктивности проводов и так далее. Эти реактивные элементы создают дополнительные фазовые сдвиги и если на какой-либо частоте они в сумме дают дополнительный угол в 180, то обратная связь превращается из отрицательной в положительную и создаются условия для паразитной генерации.

Это обстоятельство во многих случаях существенно ограничивает эффективность применения обратной связи, так как при больших значениях ½ K y K o c ½ для устранения паразитной генерации требуются специальные устройства (фазокомпенсаторы и др.), уменьшающие крутизну ФЧХ в кольце обратной связи. Однако оказывается, что введение в схему новых элементов приводит лишь к сдвигу частоты паразитной генерации в область очень низких или очень высоких частот.

Итак, из выше сказанного следует, что применение обратной связи тесно связано с проблемой обеспечения устойчивости цепи.

Для правильного построения цепи и выбора ее параметров большое значение приобретают методы определения устойчивости цепи. Рассмотрим некоторые из них.

Алгебраические критерии устойчивости.

В настоящее время известно несколько критериев, различающихся больше по форме, чем по содержанию. В основе большинства из этих критериев лежит критерий устойчивости решений дифференциального уравнения, описывающего исследуемую цепь.

Пусть линейное однородное уравнение для цепи с постоянными параметрами задано в форме :

Решение этого уравнения имеет вид :

(1)

Условие устойчивости состояния покоя цепи заключается в том, что после прекращения действия внешних возмущений цепь возвращается в исходное состояние. Для этого необходимо, чтобы возникающие в цепи при нарушении состояния покоя свободные токи и напряжения были затухающими. А это означает, что корни уравнения (1) должны быть либо отрицательными действительными величинами, либо комплексными величинами с отрицательными действительными частями. Из этих представлений вытекает следующий фундаментальный критерий устойчивости любых линейных систем :

“Cистема устойчива, если действительные части всех корней характеристического уравнения отрицательны.”

Заметим, что левая часть характеристического уравнения (1) представляет собой не что иное, как знаменатель передаточной функции цепи записанной в форме

Таким образом, корни характеристического уравнения цепи являются полюсами передаточной функции К( р ) этой цепи.

Отсюда следует, что сформулированные выше условия отрицательности действительных корней равносильны следующему утверждению : для устойчивости цепи необ-ходимо, чтобы передаточная функция К( р ) не имела полю-сов в правой полуплоскости комплексной переменной р.

В тех случаях, когда цепь описывается дифференциальным уравнением высокого порядка, исследование корней характеристического уравнения, необходимое для решения вопроса об устойчивости системы, является сложной задачей.

Однако ее можно решить, анализируя соотношения между коэффициентами уравнения без определения самих коэффициентов. Это можно сделать с помощью теоремы Гурвица, которая утверждает, что для того, чтобы действительные части всех корней уравнения

и т. д.

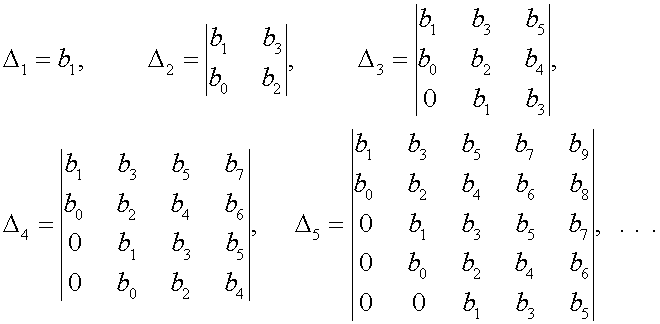
При составлении определителей по указанной схеме коэффициенты с индексом, превышающим степень характеристического уравнения заменяют нулями.

Для уравнения четвертой степени получаются следующие определители :

В результате несложно видеть, что выполняется равенство

Отсюда по теореме Гурвица следуют условия устойчивости (в виде следующих неравенств):

Так, для характеристического уравнения второй степени

Геометрические критерии устойчивости.

Требование, чтобы передаточная функция

(*)

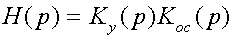
не должна обращаться в единицу ни в одной из точек правой полуплоскости р.

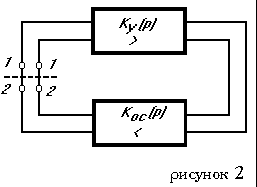
Но Н(р) представляет собой передаточную функцию разомкнутого кольца обратной связи, то есть отношение напряжения на зажимах 2-2 к напряжению на зажимах 1-1 при разомкнутой системе, как это показано на рисунке 2.

Для дальнейшего анализа перейдем от комплексной плоскости р на другую комплексную плоскость Н(р)=u+i (см. рисунок 3).

В этих выражениях аргументы передаточных функций соответственно четырехполюсников

На втором рисунке контура (см. рисунок 1) при R ® ¥ функция H(p) ® 0. Это вытекает из общего выражения

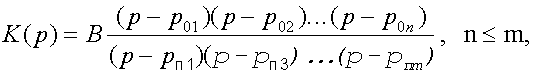
Рисунок 3 был построен для случая, когда при w = 0 передаточная функция Н(iw) отлична от нуля ( эта возможно, например, для усилителей постоянного тока, в которых отсутствуют разделительные конденсаторы).

Пример диаграммы Найквиста для неустойчивой системы приведена на рисунке 4.

Основное преимущество данного метода : удобство оперирования с АЧХ и ФЧХ разомкнутой цепи.

Для устойчивости системы тогда необходимо, чтобы годограф либо вообще не пересекал этот отрезок (так, как показано на рисунке 4), либо пересекал его в положительном и отрицательном направлениях одинаковое число раз

Литература

2. И.С. Гоноровский “Радиотехнические цепи и сигналы”, 1986 М.: Радио и связь.

Источник