22. Лекальные кривые

Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс параболу, гиперболу, циклоиду, синусоиду эвольвенту и др.

Эллипс представляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее

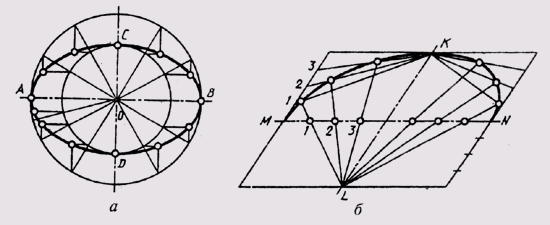
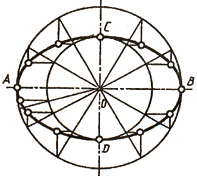
точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рис. 37, а). На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности — прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.

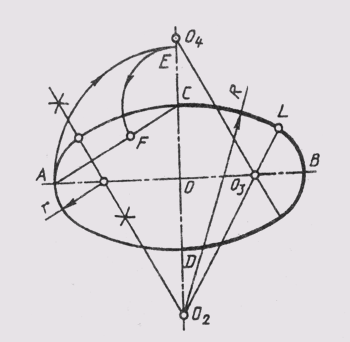
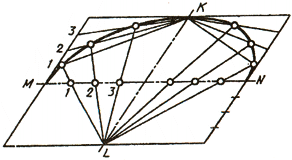
Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37,б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи. В пересечении одноименных лучей получают точки эллипса.

Параболой называют незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки — фокуса и от данной прямой — директрисы.

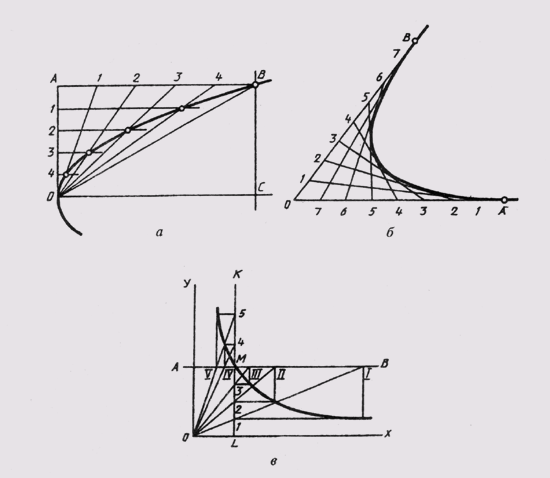
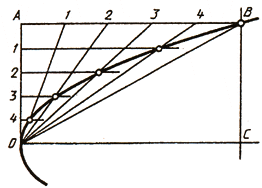
Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОABC и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.

Можно привести пример построения параболы в виде кривой, касательной прямой с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и ну-

меруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую этих прямых.

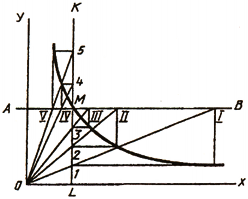
Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим асимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если асимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.

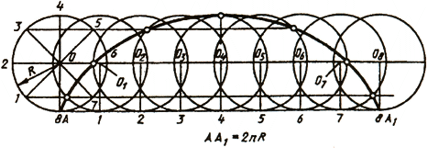
Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис. 39). Для построения циклоиды от исходного положения точки А откладывают отрезок АА], отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку 1, с окружностью, описанной из центра О₁, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, получают циклоиду.

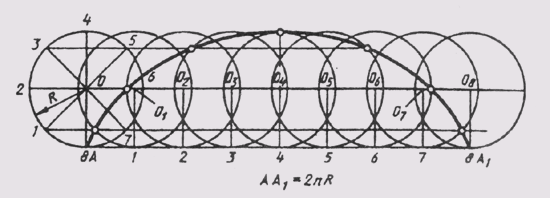
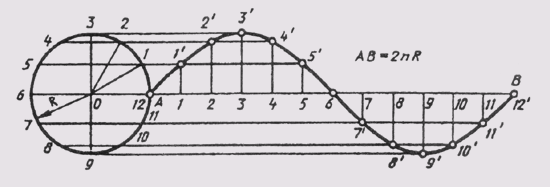
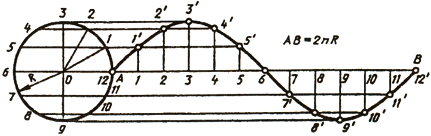
Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 40) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.

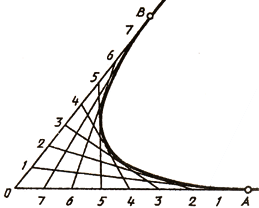
Полученные точки соединяют плавной кривой и получают эвольвенту окружности.

Источник

Глава 3. Некоторые геометрические построения

§ 22. Лекальные кривые

Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс, параболу, гиперболу, циклоиду, синусоиду, эвольвенту и др.

Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37, б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные Части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи, в пересечении которых получают точки эллипса.

Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОАВС и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.

Можно привести пример построения параболы в виде кривой, касательной прямым с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и нумеруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую зтак прямых.

Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим ассимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если ассимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.

Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис. 39). Для построения циклоиды от исходного положения точки А откладывают отрезок АА₁ отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку l, окружностью, описанной из центра О₁, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, Получают циклоиду.

Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 40) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2nR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.

© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения

Источник

Глава 3. Некоторые геометрические построения

§ 22. Лекальные кривые

Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс, параболу, гиперболу, циклоиду, синусоиду, эвольвенту и др.

Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37, б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные Части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи, в пересечении которых получают точки эллипса.

Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОАВС и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.

Можно привести пример построения параболы в виде кривой, касательной прямым с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и нумеруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую зтак прямых.

Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим ассимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если ассимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.

Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис. 39). Для построения циклоиды от исходного положения точки А откладывают отрезок АА₁ отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку l, окружностью, описанной из центра О₁, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, Получают циклоиду.

Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 40) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2nR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.

© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения

Источник

Какие кривые называются лекальными

При выполнении чертежей часто приходится прибе­гать к вычерчиванию кривых, состоящих из ряда со­пряженных частей, которые невозможно провести циркулем. Такие кривые строят обычно по ряду при­надлежащих им точек, которые затем соединяют плав­ной линией сначала от руки карандашом, а затем обво­дят при помощи лекал (рис. 71).

Рассматриваемые лекальные кривые располагаются в одной плоскости и называются поэтому плоскими.

Пространственные кривые здесь не рассматриваются.

Чтобы начертить плавную лекальную кривую, необ­ходимо иметь набор из нескольких лекал. Выбрав подходящее лекало, надо подогнать кромку части лекала к возможно большему количеству заданных точек кривой. На рис. 71 участок кривой между точ­ками 1—6 уже обведен. Чтобы обвести следующий уча­сток кривой, нужно приложить кромку лекала, напри­мер, к точкам 5—10, при этом лекало должно касаться части уже обведенной кривой (между точками 5 и 6). Затем обводят кривую между точками и 9, оставляя участок между точками 9 и 10 необведенным, что позволит получить кривую между точками 9 и 72 более плавной.

Ниже рассмотрены способы построения кривых, наиболее часто встречающихся в технике.

КРИВЫЕ КОНИЧЕСКИХ СЕЧЕНИЙ

При сечении прямого кругового конуса плоскостя­ми, различно расположенными по отношению к осям конуса, получаются контуры сечения, образующие эллипс, параболу и гиперболу.

При пересечении плоскостью P_v всех образующих конуса получается эллипс (рис. 72, а и б).

При пересечении конуса плоскостью P_v параллель­ной одной из образующих конуса (рис. 72, в), полу­чается парабола (рис. 72, г).

При пересечении конуса плоскостью P_v параллель­ной оси конуса, получается гипербола (рис. 72, и Если плоскость P_v параллельна оси конуса и прохо­дит через вершину конуса, в сечении получается тре­угольник.

Эллипс — замкнутая плоская кривая, сумма рассто­яний каждой точки которой до двух данных точек (фо­кусов), лежащих на большой оси, есть величина посто­янная и равная длине большой оси.

Широко применяемый в технике способ построения эллипса по большой (АВ)и малой (CD) осям представ­лен на рис. 72, б.

Проводят две перпендикулярные осевые линии. Затем от центра О откладывают вверх и вниз по верти­кальной оси отрезки, равные длине малой полуоси, а влево и вправо по горизонтальной оси — отрезки, рав­ные длине большой полуоси.

Из центра О радиусами О А и ОС проводят две кон­центрические окружности и ряд лучей-диаметров. Из точек пересечения лучей с окружностями проводят линии, параллельные осям эллипса, до взаимного пересечения в точках, принадлежащих эллипсу. Полу­ченные точки соединяют от руки и обводят по лекалу.

На рис. 73, а показан резервуар, контурное очерта­ние днища которого имеет форму части эллипса.

Построение очертания днища (половины эллипса) приведено на рис. 73, б. Большой осью эллипса явля­ется диаметр D цилиндрической части резервуара, а малой полуосью эллипса — наибольшее расстояние по вертикали от большой оси до днища.

Парабола — плоская кривая, каждая точка которой равноудалена от директрисы DD₁ прямой, перпендику­лярной к оси симметрии параболы, и от фокуса F — точки, расположенной на оси симметрии параболы (см. рис. 72, г).

Расстояние KF между директрисой и фокусом назы­вается параметром р параболы. Точка О, лежащая на оси симметрии, называется вершиной параболы и делит параметр р пополам.

Для построения параболы по заданной величине параметра р проводят ось симметрии параболы (на рисунке вертикально) и откладывают отрезок KF=p. Через точку К перпендикулярно оси симметрии прово­дят директрису DD₁ Отрезок делят пополам и по­лучают вершину О параболы. От вершины О вниз на оси симметрии намечают ряд произвольных точек l— VI с постепенно увеличивающимся расстоянием между ними. Через эти точки проводят вспомогательные пря­мые, перпендикулярные оси симметрии. На вспомогательных прямых из фокуса F делают засечки ради­усом, равным расстоянию от прямой до директрисы. Например, из точки F на вспомогательной прямой.

проходящей через точки делают засечку дугой R₁=KV; полученная точка 5 принадлежит параболе.

В станкостроении и других отраслях машинострое­ния часто применяются детали, контурные очертания которых выполнены по параболе, например, стойка и рукав радиально-сверлильного станка (рис. 74, б).

Построение параболы для контурного очертания рукава радиально-сверлильного станка приведено на рис. 74, в. Данными для построения являются две точки параболы А и В и направление касательных, проходящих через эти точки и пересекающихся в точке С.

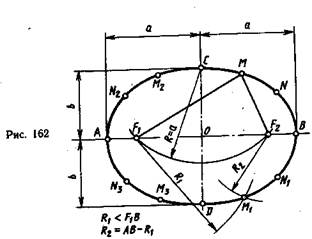
Гипербола — плоская кривая, состоящая из двух разомкнутых, симметрично расположенных ветвей (см. рис. 72, е). Разность расстояний от каждой точки гиперболы до двух данных точек (фокусов F и F₁) есть величина постоянная и равная расстоянию между вер­шинами гиперболы А и В.

Рассмотрим прием построения гиперболы по задан­ным вершинам А и В и фокусному расстоянию FF₁ (рис. 72, е).

Вторую ветвь гиперболы строят аналогичным обра­зом.

На рис. 75 показана проушина с конической поверх­ностью, срезанной двумя плоскостями, параллель­ными оси конуса, контур среза ограничен гиперболой.

СИНУСОИДА

Синусоида — плоская кривая, изображающая изме­нение синуса в зависимости от изменения угла (рис. 76, a).

Для построения синусоиды проводят горизонталь­ную ось и на ней откладывают заданную длину волны А В (рис. 76, а). Отрезок А В делят на несколько рав­ных частей, например, на 12. Слева вычерчивают окружность, радиус которой равен величине амплиту­ды, и делят ее также на 12 равных частей; точки деле­ния нумеруют и через них проводят горизонтальные прямые. Из точек деления отрезка AВ восставляют перпендикуляры к оси синусоиды и на их пересечении с горизонтальными прямыми находят точки синусои­ды.

При выполнении чертежей деталей или инструмен­тов, поверхности которых очерчены по синусоиде (рис. 76, б и в), величину длины волны обычно выбирают независимо от размера амплитуды г. Напри­мер, при вычерчивании шнека (рис. 76. б) длина волны L меньше размера 2πr. Такая синусоида называется сжатой. Если длина волны больше размера 2πr то синусоида называется вытянутой.

СПИРАЛЬ АРХИМЕДА

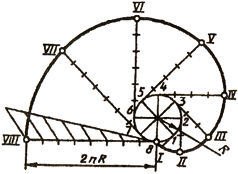
Спираль Архимеда — плоская кривая, которую описывает точка, движущаяся равномерно от центра О по равномерно вращающемуся радиусу (рис. 77).

Для построения спирали Архимеда задают ее шаг Р, из центра О проводят окружность радиусом, равным шагу Р спирали, и делят шаг и окружность на несколько равных частей (рис. 77, Точки деления нумеруют.

Из центра О проводят радиальные прямые, проходя­щие через точки деления окружности.

Из центра О радиусами 01, 02 и т. д. проводят дуги до пересечения с соответствующими радиальными пря­мыми. Например, дуга радиуса 03 пересекается с пря­мой 03₁ в точке III. Полученные точки II. VIII, принадлежащие спирали Архимеда, соединяют плав­ной кривой по лекалу.

В машиностроении спираль Архимеда применяется, например, для сообщения движения в радиальном направлении кулачкам зажимного патрона токарного станка (рис. 77, а).На тыльной стороне большой кони­ческой шестерни нарезаны канавки по спирали Архи­меда. В канавки входят выступы кулачков, которые также выполнены по спирали. При вращении шестерни кулачки будут перемещаться в радиальном направлении.

ЭВОЛЬВЕНТА

Эвольвента окружности — траектория любой точки прямой линии, перекатываемой без скольжения по окружности.

Пусть неподвижный диск диаметром D огибает шнур длиной πВ (рис. 78, а). Один конец шнура закреплен в точке А, а другой при развертывании по направлению стрелок (в натянутом положении) опишет траекторию в виде плоской кривой линии — эвольвенты.

В машиностроении профили зубьев колес и зуборез­ный инструмент — пальцевую фрезу — выполняют по эвольвенте (рис. 78, b).

Для построения эвольвенты заданную окружность диаметра D делят на несколько равных частей (на рис. 78, в — на 12 частей), которые нумеруют. Из конечной точки (72) проводят касательную к окружности и на ней откладывают отрезок, равный длине окружности πD. Длину окружности делят также на равные части.

Из точек делений окружности 1, 2,3. 12 проводят

касательные к окружности и на них откладывают отрезки; на первой касательной — отрезок 12 на второй — 12 2′ на третьей — 12 3 и т. д. Соединив точки I—XII по лекалу, получают эвольвенту окруж­ности.

ЦИКЛОИДАЛЬНЫЕ КРИВЫЕ

Циклоида — плоская кривая, которую описывает точка А, лежащая на окружности, которая катится без скольжения по прямой CD (рис. 79, а).

Эпициклоида — плоская кривая, которую описывает точка А, лежащая на окружности, которая катится без скольжения, снаружи по направляющей окружности (рис. 79, б).

Гипоциклоида — плоская кривая, которую описывает точка А, лежащая на окружности, которая катится без скольжения внутри по направляющей окружности (рис. 79, в).

Построение эпициклоиды. Производящую окружность диаметра D и направляющую окружность радиуса R проводят так, чтобы они касались (рис. 79, ). Производящую окружность диаметра D делят на 12 равных частей. Из центра 0О радиусом, равным R+0,5D, проводят вспомогательную дугу.

Источник

ЛЕКАЛЬНЫЕ КРИВЫЕ

ГЛАВА IV

КРИВЫЕ ЛИНИИ

Кривые линии встречаются в очертаниях от­дельных элементов деталей машин и механиз­мов, а также в очертаниях конструкций различ­ных строительных сооружений. Если все точки кривой линии лежат в одной плоскости, такие кривые называют плоскими кривыми.

ЛЕКАЛЬНЫЕ КРИВЫЕ

Лекальные кривые называют так потому, что они обводятся по лекалу. Принадлежащие им точки не лежат на окружностях или дугах, их строят по определенным законам, соединяют тонкой плавной линией от руки и обводят по лекалу небольшими участками. Приемы обвод­ки кривых линий по лекалу подробно рассмот­рены в § 2.

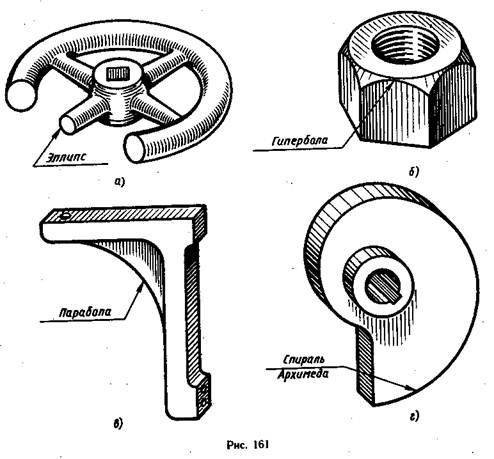
В технике часто встречаются детали, име­ющие сложные очертания, состоящие из различ­ных криволинейных участков, в том числе и из лекальных кривых. На рис. 161 показаны такие детали: маховое колесо, гайка, кронштейн, ку­лачок.

Лекальные кривые получаются при пересече­нии поверхностей плоскостями, при перемеще­нии какой-либо точки в плоскости по опреде­ленному закону, могут графически отражать за­кономерности какого-либо процесса, являться проекциями пространственных кривых и т. п. По характеру образования лекальные кривые можно разделить: на кривые конического сече­ния, циклические кривые, спирали, синусои­дальные кривые. Рассмотрим несколько кривых из каждой группы.

Кривые конического сечения — эл­липс, параболу, гиперболу — можно получить при пересечении прямого кругового конуса плоскостями различного положения по отноше­нию к образующим и оси конуса.

Эллипс — это плоская кривая линия, у которой сумма расстояний от любой точки этой кривой до двух ее фокусов (F₁ и F₂), располо­женных на большой оси, есть величина постоян­ная, равная большой оси эллипса. Например, сумма расстояний от точки М до двух фокусов F₁ F₂ (рис. 162) равна величине большой оси эллипса АБ, то есть F₁M+F₂M=AB. Эллипс всегда имеет две взаимно перпендикулярные оси (большую и малую). На рис. 162 дана боль­шая ось А В = 2а и малая ось CD = 26, требуется построить эллипс, используя для этого его фокусы. Сначала находят два фокуса F₁ и F₂. Для этого из точек С или D проводят дугу радиусом R=a до пересечения с большой осью в точках F₁ и F₂. Эти точки являются фокусами, так как точка С принадлежит эллип­су, a CF₁+CF₂=AB по построению. Для по­строения точек М, M₁, M₂, М₃ произвольным радиусом R₁ (R₁ не больше расстояния F₁B) сначала из фокуса F₁, а потом из фокуса F₂ сверху и снизу от большой оси проводят неболь­шие дуги. Второй радиус (R₂) равен разности АВ – R₁. Радиусом R₂ из двух фокусов делают засечки на четырех ранее проведенных дугах, получают точки М, M₁, M₂ и М₃. Число точек для построения очертания эллипса берется по необходимости, и все они строятся аналогично точкам М, M₁, М₂ и М₃.

Построение эллипса по заданным осям.За­даны оси эллипса АВ (большая) и CD (малая), требуется построить эллипс. Проводят две взаимно перпендикулярные прямые и от точки их пересечения (точка О) откладывают вверх и вниз по половине малой оси, а влево и впра­во— по половине большой оси (рис. 163). Из точки О описывают две концентрические окруж­ности: одну — через концы малой оси, а вто­рую — через концы большой оси. Большую окружность делят на любое число равных час­тей, например, двенадцать, все точки деления соединяют прямыми с точкой О. Эти двенадцать радиусов разделяют малую окружность тоже на двенадцать равных частей. Из всех две­надцати точек, лежащих на большой окруж­ности, проводят прямые, параллельные малой оси, а из точек, лежащих на малой окружности, проводят прямые, параллельные большой оси эллипса, до пересечения друг с другом. В пере­сечении этих прямых получают точки, принад­лежащие эллипсу. Затем эти точки соединяют от руки плавной линией и обводят по лекалу.

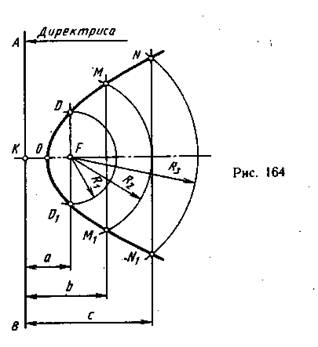
Парабола — это плоская кривая, каждая точка которой удалена на одинаковое расстоя­ние от заданной точки F (фокус) и заданной прямой ЛВ (директриса). Парабола имеет одну ось симметрии. Между директрисой и фо­кусом задается расстояние. Вершина параболы (точка О) всегда находится посередине этого расстояния, потому что она, как и любая точка параболы, должна находиться на одинаковом расстоянии от фокуса и директрисы. На рис. 164 показано построение параболы, где задано расстояние между директрисой и фокусом (от­резок KF). Через точку К проводят директрису, параллельно директрисе произвольно проводят несколько прямых. Первая прямая проведена через фокус F. Из точки F радиусом R₁=a проводят дугу до пересечения с прямой в точ­ках D и D₁. Эти точки будут принадлежать параболе, так как они находятся на одинаковом расстоянии (а) от директрисы и фокуса. Вторая прямая проведена на расстоянии b от директ­рисы. Из точки F проводят дугу радиусом R2=b до пересечения с этой прямой в точках М и M₁, которые будут принадлежать параболе, так как находятся на одинаковом расстоянии (b) от директрисы и фокуса, и т. д.

Спираль—плоская кривая, описываемая точкой, которая вращается вокруг неподвиж­ного центра и одновременно удаляется от него в соответствии с определенной закономерностью.

Спирали широко используются в технике при конструировании зажимных эксцентрико­вых приспособлений, в кулачковых патронах и механизмах, при конструировании фрез, при изготовлении плоских пружин и т. п.

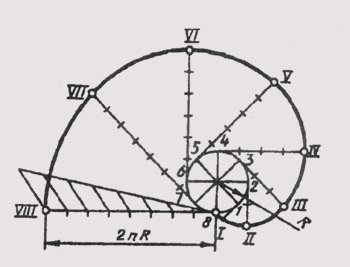
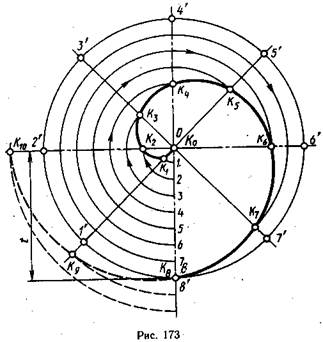
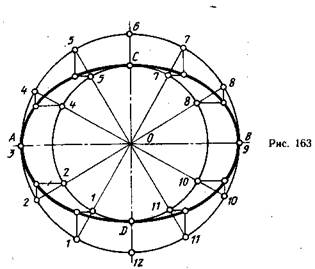
Рассмотрим способ построения спирали Архимеда с шагом t и вращением прямой по часовой стрелке. Чтобы построить спираль, необходимо зафиксировать несколько проме­жуточных положений точки и прямой, по которой она перемещается. Для этого вспо­могательная окружность, проведенная радиу­сом, равным t и отрезок 08, равный шагу, делятся на одинаковое число равных частей, например, на восемь (рис. 173). Начальная точка (К₀) совпадает с точкой О. Отрезок O₈, по которому движется точка, вращается так, что один конец (точка О) неподвижен. При повороте отрезка на 1 /₈ полного угла (45°) точка К пройдет 1 /₈ своего пути. По­этому если из центра О радиусом О₁ провести дугу до пересечения с прямой, проведенной через точку V и центр О, получим точку К и принадлежащую спирали. Если провести дугу радиусом О₂ до пересечения с прямой О₂‘, получится точка К₂, принадлежащая спирали, и т. д. При полном обороте отрезка О₈ вокруг точки О отрезок совпадает со своим началь­ным положением, а точка К займет положе­ние К₈. Полученные точки К₀…К₈ соединяют плавной линией, которую обводят по лекалу. При вычерчивании следующего витка спи­рали построение продолжают таким же обра­зом, увеличивая радиус на 1 /₈ шага. На рис. 173 это показано штриховой линией. Дальнейшеепостроение можно выполнить и другим способом. Для этого от точек К₁. К₈ откладывают по прямым О₁‘. О₈‘ отрезок, равный шагу t, получают точки К₀…К₁₆.

Эвольвента окружности — плоская кривая линия, представляющая собой траек­торию точки окружности при ее развертыва­нии. Слово «эвольвента» — латинское, озна­чает «развертывающий».

Эвольвенту окружности можно получить, если поверхность цилиндра обернуть упругой проволокой в один полный оборот и закрепить один ее конец. Отпущенный второй конец, развертываясь (распрямляясь в отрезок), опишет в пространстве кривую, которая и будет эвольвентой. При этом длина проволоки будет равна длине окружности основания данного цилиндра (2πR).

Такую же кривую описывает любая точка прямой линии, катящейся без скольжения по окружности. Эвольвента используется при профилировании кулачков, эксцентриков, зубьев зубчатых передач и т. п.

Если окружность разделить на любое число равных дуг и представить развертывание и выпрямление каждой дуги в отрезок прямой линии, то полученные отрезки будут касательными к заданной окружности. Точки касания будут точками окончания каждой дуги кото­рые будут одновременно начальными точками следующих дуг. А как известно, касательная перпендикулярна к радиусу окружности проведенному в точку касания.

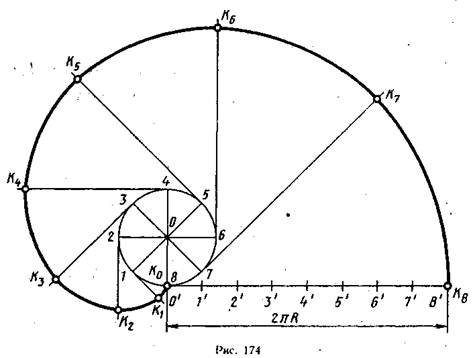
На рис. 174 показано построение эвольвентыокружности. Заданную окружность делят на любое число равных дуг (в данномслучае на восемь), получают точки 1. 8. Каждую точку деления соединяют с центром окружности (точка О). Из точки 8 проводят касательную к окружности и откладывают на ней длину окружности (2πR). Этот отрезок будет развернутой окружностью. Точка 8′ будет принадлежать эвольвенте. Затем полу­ченный отрезок делят на восемь равных частей и получают отрезки, равные 1 /₈ длины окружности, для определения длины каждой развернутой дуги. Далее через точки 1. 8 проводят касательные и откладывают отрезки, равные длине соответствующей дуги. От точки 1 откладывают отрезок, равный длине развернутой дуги О׳1′. От точки 2 — отрезок, равный длине развернутой дуги О’2׳ и т. д. Получают точки K₁. К₈, принадлежащие эвольвенте. Полученные точки соединяют плавной кривой линией, которую обводят по лекалу.

Синусоида — плоская кривая линия, изображающая изменение синуса в зависи­мости от изменения угла а. Она используется в построении проекций винтовых линий.

Источник