какие математические алгоритмы используются в электронной подписи
Принцип использования электронной цифровой подписи
Общее
Определение подлинности информации реализуется путем установки факта, что полученные данные была отправлена подписавшим электронно цифровой подпись, и то что данные не были искажены. На сегодня словосочетание электронная цифровая подпись стало обыденным, а еще не давно считалось что электронный документ проще подделать чем бумажный экземпляр. Письменная подпись под документом используется в качестве доказательства, что человек согласен с содержимым документа. Основные причины доверия к подписи:
В нашем современном криминальном обществе, ни одно из перечисленных свойств на все 100% не реализуются. Можно и подделать подпись, и убрать но это реализуется не просто и быть пойманным есть риск. Существуют также дополнительные вопросы, при отправки документа по почте. Любой документ можно скопировать вместе с подписью. Также можно внести из мнения после подписания документа. Для ликвидации таких угроз используют электронно цифровую подпись. Подделать подпись очень сложно, так как она создается на основе большого объема математических операций. Цифровая подпись может хранится вместе с документом, или быть отдельно от него.
Электронно цифровая подпись — это метод который позволяет на основе реализации криптографических средств определить автора и подлинность документа. Преимущества электронно цифровой подписи:
Возможные угрозы которые наносят ущерб развитию электронного документооборота показаны на рис.1. Эти угрозы:
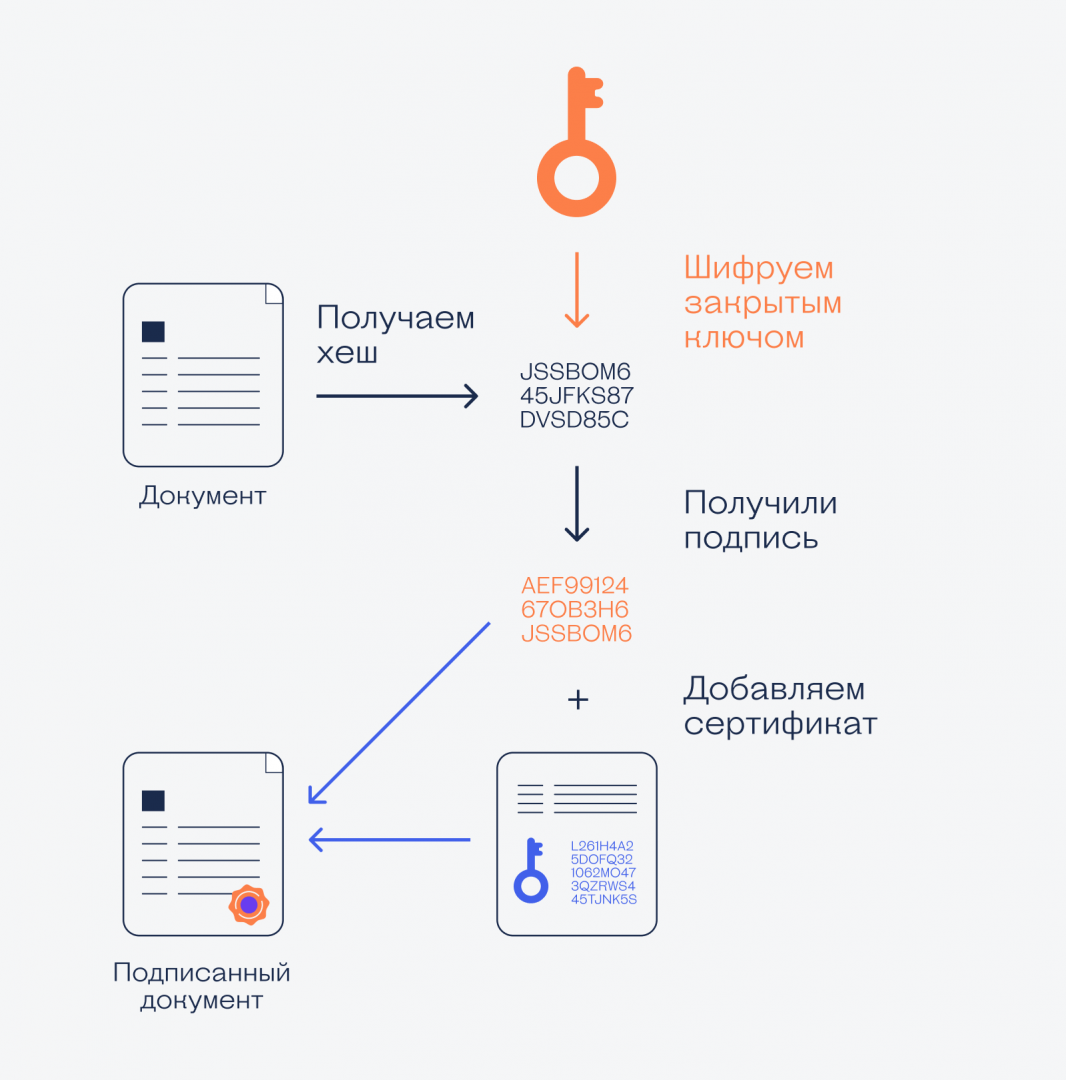
В рамках классической криптографии для аутентификации трудно защитится от всех видом угроз. Эффективно используют схемы подписания, где реализована двухключевая криптография. В этой ситуации каждый пользователь имеет свой секретный ключ. Передающий пользователь несет ответственность за свой секретный ключ. Никто кроме него не может подписать документ именно с такой подписью. К такому ключу можно провести аналогию, как с печаткой. Электронная подпись являет собой длинной число, на основе хеш-функции документа.
Криптостойкость цифровой электронной подписи должна реализовывать надежность к подделкам людьми, которые не имеют секретный ключ. Также должно быть обеспечена защита НСД к месту хранения секретного ключа.
Алгоритмы электронной цифровой подписи
Технология реализации системы ЭЦП означает наличие в сети пользователей, которые посылают друг другу подписанные электронные документы. Для каждого пользователя генерируется пара ключей: открытый и секретный. Сектрекный ключ держится абонентом в тайне и реализуется для формирования ЭЦП получателем подписанного электронного документа. Открытый ключ не разрешает вычислить секретный ключ. При генерации пары ключей в алгоритмах ЭЦП, как и в асимметричных системах шифрования, реализованы разные математические схемы, которые основаны на однонаправленых функциях. Эти функции можно разделить на две группы:
Алгоритм цифровой подписи RSA
Первая и самая встречаемая система ЭЦП на основе RSA. Сначала нужно вычислить пару ключей. Отправитель (автор) электронных документов вычисляет два больших простых числа P и Q, затем находит произведение и значение функции:
Затем отправитель вычисляет число Е из условий:
Е £ φ (N), НОД (Е, φ (N)) = 1
Алгоритм цифровой подписи Эль Гамаля (EGSA)
Основная идея обоснована на практической невозможности фальсификации цифровой подписи. Для этого нужна более сложная вычислительная задача, чем разложение на множители большого целого числа. Также Эль гамалю удалось избежать слабости алгоритма ЭЦП RSA, связанной с подделкой ЭЦП без определения секретного ключа.
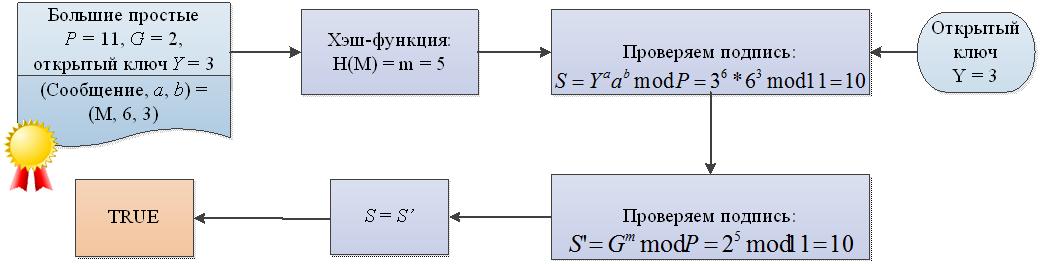
Что бы генерировать пару ключей, нужно выбрать простое целое число P и G, причем G 308 =
1 512 ) которые не секретные. Отправитель выбирает случайное целое число X, 1 X mod P;
Число Y является открытым ключом, который используется для проверки подписи отправителя. Число Х является секретным ключом отправителя для подписи документов. Что бы подписать сообщение М, сначала нужно что бы отправитель захэшировал его с помощью хэш-функции h в целое число m: m = h(M), 1 K mod P; используя расширенный алгоритм Евклида, вычисляет с помощью секретного ключа Х целое число b: m = X * a + K * b (mod (P — 1)); Пара чисел (a, b) образуют цифровую подпись S: S = (a, b);
Тройка чисел (M, a, b) транспортируется получателю, в то время как пара чисел (X, K) держится в секрете. Получатель получив сообщение (M, a, b) должен вычислить число m: m = h(M). затем получатель вычисляет: A = Y a a b mod (P), и признает сообщение M подлинным, если — A = G m mod (P). Можно строго математически доказать, что последнее равенство будет равно тогда, когда подпись S под документом M получена с помощью именно секретного ключа X, из которого был получен открытый ключ Y. Нужно отметить, что процедура каждой подписи требует нового значения К, и выбирается случайным образом.
Схема Эль Гамаля является типичным примером, который разрешает пересылку сообщений М в открытой форме вместе с аутентификатором (a, b). Такая схема имеет преимущества перед схемой ЭЦП RSA:
К недостаткам можно отнести то, что подпись получается в 1,5 раза больше чем RSA.
Алгоритм цифровой подписи DSA
DSA — Digital Signature Algorithm — это развитие алгоритмов цифровой подписи Эль Гамаля и К.Шнорра. Получатель и отправитель электронного документа реализуют при вычислении большие целые числа G и P — простые числа, L бит каждое (512 £ L £ 1024), q — простое число длинной 160 бит (делитель числа (P — 1)). Числа P, G, q есть открытыми и могут быть общими для пользователей. Отправитель берет случайное целое число X, 1 X mod P. Число Y — открытый ключ. Что бы подписать документ М, отправитель хэширует его в целое хэш-значение m: m = h(M), 1 K mod P) mod q. Также нужно вычислить: s = ((m + r * X)/ K) mod q; Пара чисел S = (r, s) образуют цифровую подпись. Получатель проверяет выполнение условий: 0 u1 * Y u2 ) mod P) mod q; Если условие v = r выполняется, тогда подпись S под документом подлинная.
Можно математически доказать, что последнее равенство будет выполнятся тогда, когда подпись S под документом получена с помощью секретного ключа X, из которого был получен открытый ключ Y. Алгоритм DSA имеет преимущества над ЭЦП Эль Гамаля:
Недостатками алгоритма является то, что при проверке подписи нужно реализовывать сложные операции деления по модулю q. Следует отметить, что реальное исполнение алгоритма DSА может быть ускорено с помощью выполнения предварительных вычислений. Заметим, что значение r не зависит от сообщения М и его хэш-значения m.
Как работает электронная подпись
Одно из полезных применений асимметричного шифрования — работа с электронной подписью. Рассказываем, как устроена ЭП изнутри и где она применяется.
Что такое электронная подпись
Электронная подпись — это технология, которая помогает подтвердить подлинность электронного документа: договора, справки, выписки или чего-то ещё.
Если упрощённо, работает так:
👉 Есть некий документ, подписанный ЭП
👉 С помощью специальной программы можно проверить подлинность этой подписи и документа
✅ Если программа говорит, что всё окей, то мы можем быть уверены: документ подписал именно тот, кто в нём указан; и с момента подписания в документе ничего не изменилось.
❌ Или программа может сказать, что подпись не совпала. Это значит, что либо документ подписал другой человек, либо после подписания кто-то изменил этот документ (например, дописал ноль в стоимость контракта). Так мы поймём, что этому документу нельзя доверять.
С технической точки зрения ЭП — небольшой файлик, который прилагается к искомому документу. Файлик пересылается вместе с основным документом, его можно передавать по открытым каналам связи, в нём нет ничего секретного.
Электронная подпись нужна, чтобы защищать договоры, выдавать официальные справки, заключать сделки и участвовать в торгах по госзакупкам.
Основа ЭП — асимметричное шифрование
Как работает: сертификаты
Электронная подпись состоит из двух принципиальных частей:
Грубо говоря, ЭП должна гарантировать, что документ подписали именно вы и что вы подписали именно этот документ.
В сертификате хранятся данные о владельце подписи:
Но смысл сертификата не в том, что там хранятся эти данные, а в том, кто эти данные туда положил. В России сертификаты и ЭП выдают специальные удостоверяющие центры — это компании, которые гарантируют, что сертификат выдаётся именно тому, кто в этом сертификате указан.
Чтобы получить сертификат, вы приходите лично в эту компанию (удостоверяющий центр), показываете документы, фотографируетесь. Вас заносят в базу удостоверяющего центра и выдают ключи электронной подписи. Так все участники электронного документооборота будут уверены, что все документы, подписанные вашими ключами, подписаны именно вами.
Как работает: алгоритмы шифрования
Допустим, вы уже сходили в удостоверяющий центр и получили на флешке сертификат и ключ электронной подписи. Теперь нужно скачать специальный софт, который и будет подписывать ваши документы и проверять чужие на подлинность.
Проблема в том, что ЭП основана на алгоритмах асимметричного шифрования, а их много: разложение на простые множители, дискретное логарифмирование, эллиптические кривые и множество других. Ключ из одного алгоритма не подойдёт для использования в другом, поэтому в России договорились использовать стандарт шифрования ГОСТ Р 34.10-2012, основанный на эллиптических кривых. Все государственные органы работают только с таким алгоритмом и не принимают другие ЭП.
Это значит, что нам нужен специальный софт, в котором уже есть этот алгоритм. Чаще всего используют КриптоПРО, реже — ViPNet CSP. С помощью этих программ можно подписать документы и проверить сертификаты на подлинность.
Принцип работы электронной подписи
Электронная подпись — это асимметричное шифрование наоборот: вы зашифровываете закрытым ключом, а расшифровать может кто угодно с помощью открытого ключа, который доступен всем.
👉 Если открытый ключ подходит к сообщению и расшифровывает его, значит, оно было зашифровано именно этим закрытым ключом — то есть именно вами.
А что если подменят сам сертификат?
Все сертификаты, которые выдаёт удостоверяющий центр, тоже подписываются электронной подписью. Чтобы проверить подлинность сертификата, можно зайти на официальный сайт удостоверяющего центра и скачать открытый ключ для проверки. Если хеш самого сертификата совпадает с хешем, который мы получили с помощью открытого ключа с сайта — значит, и сам сертификат подлинный.
Как работает электронная подпись
Из нашей статьи вы узнаете:
ЭЦП — электронная (цифровая) подпись — это аналог рукописной подписи. Она выполняет ту же функцию — обеспечивает юридическую значимость для документов. Только подписывают с помощью ЭЦП документы не бумажные, а электронные. Кроме того, электронная подпись фиксирует информацию, которая была в документе на момент подписания, тем самым подтверждая её неизменность.
Как устроена электронная подпись
Электронная подпись состоит из двух основных частей:
Эти составные части выполняют разные функции: с помощью закрытого ключа, доступного только владельцу, документ шифруется, а с помощью сертификата, доступного для всех, документ дешифруется. Таким образом, достигается цель использования ЭЦП — подтверждается то, кем был подписан документ, и заверяется его неизменность с момента подписания.
Закрытый ключ не содержит в себе ничего, кроме механизма, с помощью которого он может шифровать документы. Сертификат же несёт в себе такую полезную информацию, как сведения о владельце, сведения об удостоверяющем центре, срок действия электронной подписи и т.д. Сертификат выступает в роли главного носителя информации о ЭЦП.
Программы для работы и алгоритмы шифрования
Чтобы шифровать и подписывать документы, недостаточно только иметь сертификат и закрытый ключ, для работы нужно устанавливать специальные программы. С помощью этих программ, которые работают по определённому стандарту шифрования (в России — ГОСТ Р 34.10-2012), обеспечивается связь закрытого и открытого ключа с документами.
Самой популярной программой-криптопровайдером в России является «КриптоПро CSP». С её помощью можно подписывать и шифровать документы, проверять сертификаты на подлинность, контролировать целостность соответствующего программного обеспечения.
Принцип работы электронной подписи
Электронная подпись работает по ассиметричному принципу шифрования. То есть документ зашифровывается с помощью закрытого ключа, а расшифровывается с помощью открытого.
Подписание документа производится в несколько этапов:
Так как сертификаты, выдаваемые удостоверяющим центром, так же подписываются с помощью электронной подписи, подменить сертификат невозможно. На сайте удостоверяющего центра, как правило, можно скачать открытый ключ проверки, хеш которого должен совпадать с хешем открытого ключа владельца. Таким образом доказывается его достоверность.
Приобрести квалифицированную электронную подпись можно только в удостоверяющем центре, аккредитованном Минкомсвязи. УЦ «Астрал-М» предлагает надёжную и безопасную подпись «Астрал-ЭТ». Чтобы получить электронную подпись, достаточно выполнить четыре действия:
Гайд по криптографии: что такое электронная цифровая подпись и как она работает
Содержание статьи
Roadmap
Это пятый урок из цикла «Погружение в крипту». Все уроки цикла в хронологическом порядке:
Как работает цифровая подпись
Если вспомнить формальное определение, то ЭЦП — это реквизит электронного документа. Другими словами, последовательность битов, вычисленная уникально для каждого конкретного сообщения. Подпись может быть вычислена как с применением секретного ключа, так и без него. Без секретного ключа подпись представляет собой просто код, который может доказать, что документ не был изменен. С использованием секретного ключа подпись докажет целостность сообщения, позволит убедиться в его подлинности и аутентифицировать источник.
Если ты читал вторую часть нашего цикла, то помнишь, что существуют симметричный и асимметричный подходы к шифрованию. С электронной подписью дела обстоят очень похоже — есть подписи с симметричным механизмом, а есть с асимметричным.
Симметричный механизм подписи малоприменим на практике — никому не хочется генерировать ключи для каждой подписи заново. А как ты помнишь, именно в одинаковых ключах кроется фишка симметричной криптографии.
Схемы электронной подписи так же многообразны, как и способы шифрования. Чтобы схема подписи была стойкой, нужно, чтобы она основывалась на трудновычислимой математической задаче. Есть два типа таких задач: факторизация больших чисел и дискретное логарифмирование.
Факторизация больших чисел
Рассмотрим на практике электронную подпись на основе знаменитого алгоритма RSA. Шифрование RSA мы рассматривать не стали — это мейнстрим, и в той же «Википедии» есть его подробное описание.
1. Генерация ключей
Причина стойкости RSA кроется в сложности факторизации больших чисел. Другими словами, перебором очень трудно подобрать такие простые числа, которые в произведении дают модуль n. Ключи генерируются одинаково для подписи и для шифрования.
Когда ключи сгенерированы, можно приступить к вычислению электронной подписи.
2. Вычисление электронной подписи
3. Проверка электронной подписи
RSA, как известно, собирается уходить на пенсию, потому что вычислительные мощности растут не по дням, а по часам. Недалек тот день, когда 1024-битный ключ RSA можно будет подобрать за считаные минуты. Впрочем, о квантовых компьютерах мы поговорим в следующий раз.
В общем, не стоит полагаться на стойкость этой схемы подписи RSA, особенно с такими «криптостойкими» ключами, как в нашем примере.
Дискретное логарифмирование
Это вторая сложная проблема, на которой основаны цифровые подписи. Для начала хорошо бы усвоить, что такое дискретный логарифм. Для кого-то такое словосочетание может звучать пугающе, но на самом деле это одна из самых простых для понимания вещей в этой статье.
1. Генерация подписи
2. Проверка подписи
Даже если не вникать в схему, понятно, что такой алгоритм сложнее. Кроме того, нигде уже не используется простой модуль, его сменили эллиптические кривые. Эллиптическая кривая — это кривая, которая задана кубическим уравнением и имеет невообразимо сложное представление. Задача решения логарифма в группе точек, которые принадлежат эллиптической кривой, вычислительно сложная, и на данный момент не существует таких мощностей, которые решали бы это уравнение за полиномиальное время, если длина секретного ключа составляет 512 бит. Согласно задаче дискретного логарифмирования, невероятно сложно найти на кривой две такие точки, которые связывает операция возведения в некоторую степень.
ЭЦП на практике
В России, как и во многих развитых странах, электронная подпись имеет официальный юридический статус. У нас этот факт регламентирует закон № 63-ФЗ «Об электронной подписи». Однако он утверждает, что юридической силой обладает далеко не любая электронная подпись, а только соответствующая определенным критериям:
Подпись также должна быть вычислена средствами, соответствующими требованиям закона. Этим требованиям удовлетворяет отечественный алгоритм шифрования ГОСТ 34.10—2012. Он использует математический аппарат эллиптических кривых, является достаточно стойким и официально используется для разработки криптографических средств, реализующих электронную подпись. Для того чтобы попробовать неквалифицированную подпись — без сертификата удостоверяющего центра, можно воспользоваться известной PGP. Потестировать подпись можно, к примеру, на сайте ReadVerify.
Стоит сказать, что в нашей стране электронная подпись используется чаще, чем можно себе представить. В банках, налоговых, торгово-закупочных операциях, бухгалтерии — во всех этих организациях используется или внедряется ЭЦП. Электронная подпись отважно борется со злом бюрократии, однако до полной победы еще далеко.
За рубежом электронный документооборот процветает еще дольше. Официальный стандарт электронной подписи в США DSS (Digital Signature Standard) также использует эллиптические кривые и основан на описанной выше схеме Эль-Гамаля.
Цифровая подпись в Bitcoin
Помимо прочего, электронная подпись используется в криптовалютах, в частности — в Bitcoin. У каждого пользователя Bitcoin есть пара из секретного и открытого ключа. Хеш-значение открытого ключа служит основным адресом для передачи монет. Это значение не секретно, и сообщать его можно кому угодно. Но по значению хеша вычислить значение открытого ключа невозможно.
Сама пара ключей будет использована лишь однажды — при передаче прав собственности. На этом жизнь пары ключей заканчивается.
Вот как устроен сам процесс передачи прав собственности на биткойны.
О втором собственнике ничего не известно, кроме HASH(PUB2), до тех пор пока он не передаст права третьему владельцу. И эта цепочка может быть бесконечной.
Подписывая передачу прав с использованием ЭЦП, собственник подтверждает не только свою личность, но и свое согласие на проведение сделки. То есть вернуть монетку он уже не может и с этим согласился, подписавшись электронной подписью.
Благодаря HASH(PUB) получается двойная защита. Первая загадка — узнать публичный ключ по его хешу. Вторая загадка — подписаться чужим секретным ключом.
Такая технология построения цепи передачи прав и называется блокчейном. Благодаря этой технологии можно отследить историю владения до самых истоков, но изменить эту историю никак нельзя.
Выводы
Будущее неразрывно связано с криптографией. В один прекрасный момент при получении паспорта наши дети будут генерировать электронную подпись и покупать чипсы в ларьке за криптовалюту. Что готовит нам будущее с точки зрения развития криптографии, посмотрим в следующей статье на примере квантовых компьютеров.
RSA: от простых чисел до электронной подписи
Выясняем, как и откуда можно получить электронную подпись на примере криптосистемы RSA.

Определения и обозначения
Описание криптосистемы RSA
Асимметричные криптографические системы
Шифрование и дешифрование
Получение подписи сообщения по RSA
Электронная подпись документов
Введение
Наверняка вы сталкивались с таким понятием, как «электронная подпись». Если обратиться к федеральному закону, то можно найти следующее её определение:
Задача ЭП ясна, теперь хотелось бы увидеть и прочувствовать, что именно скрывается за этими двумя словами. Копаясь дальше в гугле, можно найти довольно много различных алгоритмов создания цифровой подписи (DSA, ГОСТ Р 34.10-2012, RSA-PSS и т.д.), разбираться в которых неподготовленному пользователю сложно.
Спасти эту ситуацию и помочь разобраться в том, что есть ЭП, может криптосистема RSA, разработанная Ривестом, Шамиром и Адлеманом в 1978 году. Она не загромождена безумным количеством алгоритмов и основывается на относительно простой математике. В связи с этим можно шаг за шагом прийти от модульной арифметики к алгоритму создания электронной подписи, чему я и хочу посвятить данную статью.
Теорминимум
Сформируем небольшой словарик терминов, которые нам пригодятся далее:
Открытый текст – данные, подлежащие шифрованию или полученные в результате расшифрования
Шифртекст – данные, полученные в результате применения шифра к открытому тексту
Шифр – совокупность обратимых преобразований, зависящая от некоторого параметра (ключа)
Ключ – параметр шифра, определяющий выбор одного преобразования из совокупности.
Факторизация – процесс разложения числа на простые множители.
НОД – наибольший общий делитель.
Числа a и b называются взаимно простыми, если НОД этих чисел равен 1.
Функция Эйлера φ(n) – функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним.
Хочу отметить, что на данном этапе подразумевается, что вы знакомы с арифметическими операциями по модулю. Если нет, то здесь можно о них почитать.
Как оно устроено
Прежде, чем окунуться в необъятный мир математики рассмотреть, как именно устроена RSA, обратимся к тому, как работают
Асимметричные криптосистемы
Рассмотрим задачу сохранности содержимого посылки при передаче от отправителя к адресату. Вот картинка с многим полюбившимся Алисой и Бобом:
Алиса хочет передать Бобу посылку. Для начала Боб на своей стороне создает уникальные замок и ключ к нему (открытый и закрытый ключ соответственно). Далее, Боб делится с окружающим миром своим замком, чтобы любой желающий отправить ему посылку смог её закрыть. Поскольку ключ от подобного замка один и находится только у Боба, никто, кроме Боба, просмотреть содержимое после защёлкивания замка не сможет. В конце концов, Алиса с помощью полученного замка закрывает посылку и передаёт Бобу, который открывает её своим ключом. Таким образом устроены асимметричные криптографические системы, которой как раз является RSA.
В схеме передачи посылки все объекты вполне материальны. Однако сообщения, которые мы хотим шифровать, являются ничем иным, как последовательностью бит, которую нельзя «закрыть» на физический замок. Таким образом возникают вопросы: что такое ключ и замок? Как Бобу создать ключи? Каким образом ключи связаны и как с их помощью зашифровать сообщение? Здесь нам поможет математика.
Теперь к математике
Асимметричные криптографические системы основаны на так называемых односторонних функциях с секретом. Под односторонней понимается такая функция я y=f(x), которая легко вычисляется при имеющемся x, но аргумент x при заданном значении функции вычислить сложно. Аналогично, односторонней функцией с секретом называется функция y=f(x, k), которая легко вычисляется при заданном x, причём при заданном секрете k аргумент x по заданному y восстановить просто, а при неизвестном k – сложно.
Подобным свойством обладает операция возведения числа в степень по модулю:
Здесь φ(n) – функция Эйлера числа n. Пока условимся, что это работает, далее это будет доказано более строго. Теперь нужно понять, что из это является ключами Боба, а что сообщением. В нашем распоряжении имеются числа c, m, n, e, d.
Давайте посмотрим на первое выражение. Здесь число c получено в результате возведения в степень по модулю числа m. Назовём это действие шифрованием. Тогда становится очевидно, что m выступает в роли открытого текста, а c – шифртекста. Результат c зависит от степени e, в которую мы возводим m, и от модуля n, по которому мы получаем результат шифрования. Эту пару чисел (e, n) мы будем называть открытым ключом. Им Алиса будет шифровать сообщение.
Смотрим на второе действие. Здесь d является параметром, с помощью которого мы получаем исходный текст m из шифртекста c. Этот параметр мы назовём закрытым ключом и выдадим его Бобу, чтобы он смог расшифровать сообщение Алисы.
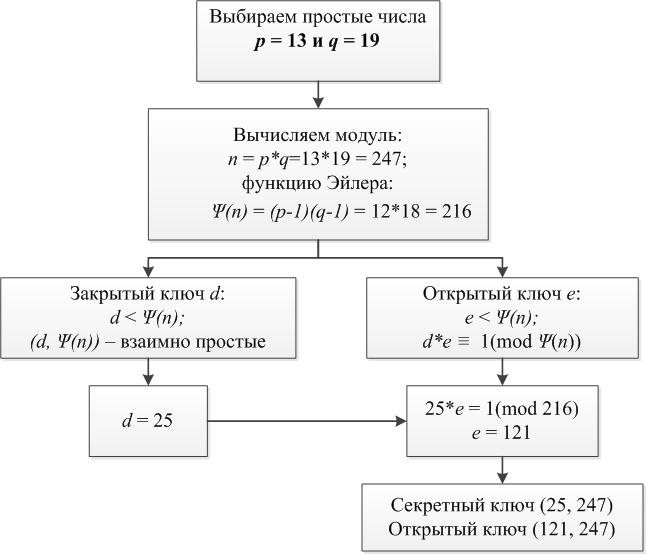
Что есть что разобрались, теперь перейдём к конкретике, а именно – генерации ключей Боба. Давайте выберем число n такое, что:
где p и q – некоторые разные простые числа. Для такого n функция Эйлера имеет вид:
Такой выбор n обусловлен следующим. Как вы могли заметить ранее, закрытый ключ d можно получить, зная открытый e. Зная числа p и q, вычислить функцию Эйлера не является вычислительно сложной задачей, ровно как и нахождение обратного элемента по модулю. Однако в открытом ключе указано именно число n. Таким образом, чтобы вычислить значение функции Эйлера от n (а затем получить закрытый ключ), необходимо решить задачу факторизации, которая является вычислительно сложной задачей для больших n (в современных системах, основанных на RSA, n имеет длину 2048 бит).
Возвращаемся к генерации ключей. Выберем целое число e:
Для него вычислим число d:
Для отыскания числа, обратного по модулю, можно воспользоваться алгоритмом Евклида.
Мы завершили с этапом генерации ключей. Теперь Боб публикует свой открытый ключ (e, n), прячет закрытый d, а мы переходим к Алисе.
Шифруем, дешифруем.
Возьмём в качестве сообщения число m (m ∈ [1, n − 1]). Чтобы Алисе зашифровать его, необходимо возвести его в степень e по модулю n. Эти числа идут вместе с открытым ключом Боба:
Здесь за с обозначен шифртекст, который Алиса будет должна передать Бобу. Отметим также, что c ∈ [1, n − 1], как и m. Расшифруем шифртекст, возведя его в степень закрытого ключа Боба d:
Здесь нам понадобится теорема Эйлера:
Также полезной будет китайская теорема об остатках:
Получаем подпись сообщения
Ещё раз напишем две ключевые формулы шифрования и расшифрования соответственно:
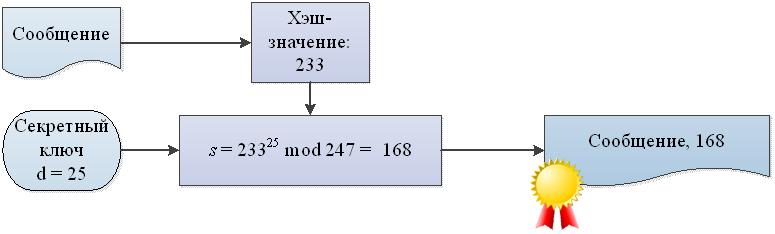
Теперь давайте предположим, что Боб хочет отправить Алисе открытку m от своего имени. У Боба в распоряжении уже имеются два ключа (e, n) и d, которые он сгенерировал по алгоритму, описанному ранее. Поскольку d является закрытым ключом, то можно им воспользоваться как уникальным идентификатором Боба. Давайте «зашифруем» m с помощью d:
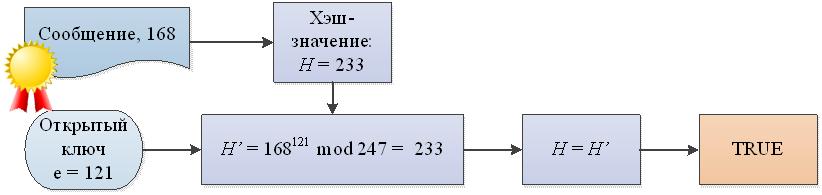
Результат данной операции и есть подпись сообщения Боба. Заметим, что подпись напрямую зависит от подписываемого сообщения, а не только от того, что его подписывает Боб. Далее, Алиса получает сообщение m, подпись s и открытый ключ (e, n). По аналогии с расшифрованием, проверка подписи осуществляется возведением подписи s в степень открытой экспоненты e:
Если Алиса получила, что m ≡ m′, то подпись считается правильной.
Дочитавших до этого места хочу поздравить с получением первой цифровой подписи «на бумаге»!
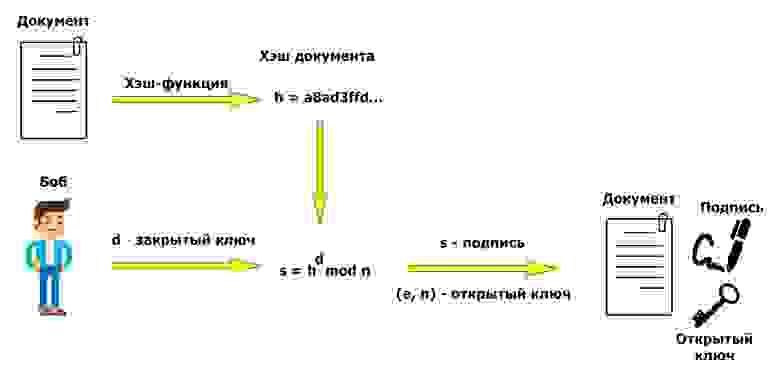
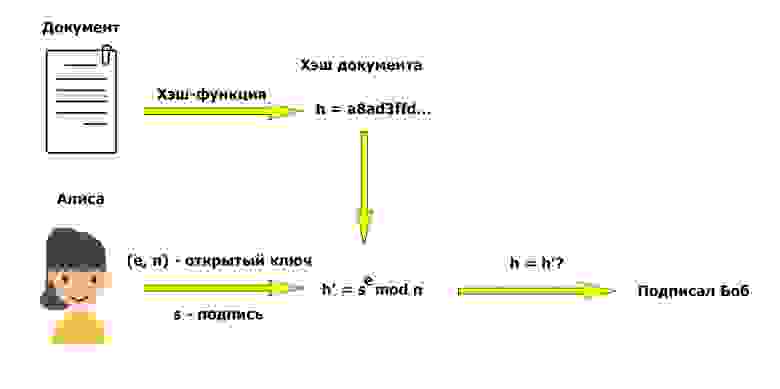
Подпись документов
Рассмотренный алгоритм получения подписи изящен и прост в осознании, однако операция возведения в степень несколько «мешается». Наша текущая задача – подписать объёмный документ. Чтобы сэкономить время, мы не будем подписывать содержимое документа, а прибегнем к помощи хэш-функций (если вы не знаете, что такое хэш-функция, рекомендую почитать википедию). Скажу лишь то, что выходная последовательность хэш-функции имеет небольшую (по сравнению с размером ключей) длину, а также по имеющемуся хэшу нельзя однозначно восстановить исходные данные.
На картинках наглядно показано, в какой момент мы используем хэширование. Создание подписи:
В качестве хэш-функции можно использовать SHA-256, как это сделано, например, в PGP. По теме практического создания электронной подписи с использованием PGP на хабре уже написана статья, поэтому на этом месте имеет смысл поставить точку и перейти к заключению.
Заключение
Вот мы и прошли все стадии создания электронной подписи, начиная с простой модульной арифметики и заканчивая, собственно, получением подписи. Обладая этими знаниями, вы можете попробовать перевести их на ваш любимый язык программирования и написать свою защищенную аську, например. В том, как именно их применить, вас ограничит только ваше воображение.
Отмечу, что другие существующие алгоритмы создания ЭП основаны на схожих принципах, поэтому надеюсь, что после прочтения этой статьи вам будет проще разобраться в них. «Следующей по сложности» я обозначу криптосистему Эль-Гамаля, но о ней уже не в этом посте.
Спасибо за внимание!
Источники
Handbook of Applied Cryptography by A. Menezes, P. van Oorschot and S. Vanstone
Криптографические методы защиты информации: учеб. пособие / С. М. Владимиров, Э. М. Габидулин, А. И. Колыбельников, А. С. Кшевецкий; под ред. А. В. Уривского. – М.: МФТИ, 2016
Маховенко Е. Б. Теоретико-числовые методы в криптографии — М.: Гелиос АРВ, 2006.
NIST Special Publication 800-57 Part 3 Revision 1