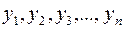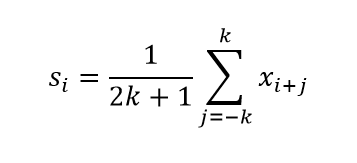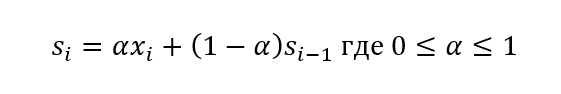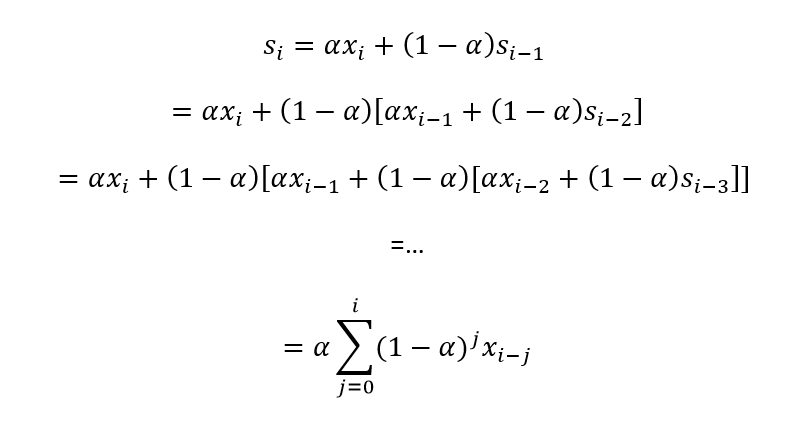какие методы используются для сглаживания временного ряда
Методы сглаживания временных рядов.
Очень часто, урони рядов динамики колеблются, при этом тенденция развития явления во времени скрыта случайными отклонениями уровней в ту или иную сторону. С целью более четко выявить тенденцию развития исследуемого процесса, в том числе для дальнейшего применения методов прогнозирования на основе трендовых моделей, производят сглаживание (выравнивание) временных рядов.
Методы сглаживания временных рядов делятся на две основные группы:
1. аналитическое выравнивание с использованием кривой, проведенной между конкретными уровнями ряда так, чтобы она отображала тенденцию, присущую ряду, и одновременно освобождала его от незначительных колебаний;
2. механическое выравнивание отдельных уровней временного ряда с использованием фактических значений соседних уровней.
Суть методов механического сглаживания заключается в следующем. Берется несколько уровней временного ряда, образующих интервал сглаживания. Для них подбирается полином, степень которого должна быть меньше числа уровней, входящих в интервал сглаживания; с помощью полинома определяются новые, выровненные значения уровней в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один уровень ряда вправо, вычисляется следующее сглаженное значение и так далее.
Самым простым методом механического сглаживания является метод простой скользящей средней.
2.4.1. Метод простой скользящей средней.
Сначала для временного ряда: 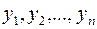

| При прочих равных условиях интервал сглаживания рекомендуется брать нечетным. |
Для первых 

где 


В результате такой процедуры получаются 


2.4.2. Метод взвешенной скользящей средней.
Метод взвешенной скользящей средней отличается от предыдущего метода сглаживания тем, что уровни, входящие в интервал сглаживания, суммируются с разными весами. Это связано с тем, что аппроксимация ряда в пределах интервала сглаживания осуществляется с использованием полинома не первой степени, как в предыдущем случае, а степени начиная со второй.
Используется формула средней арифметической взвешенной:

причем веса 
1. для полиномов второго и третьего порядков числовая последовательность весов при интервале сглаживания 



2. для полиномов четвертой и пятой степеней и при интервале сглаживания 
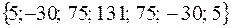
Распределение весов на протяжении интервала сглаживания, полученное на основе метода наименьших квадратов см. на диаграмме 1.
 |
2.4.3. Метод экспоненциального сглаживания.
К той же группе методов относится метод экспоненциального сглаживания.
Его особенность заключается в том, что в процедуре нахождения сглаженного уровня используются значения только предшествующих уровней ряда, взятые с определенным весом, причем вес наблюдения уменьшается по мере удаления его от момента времени, для которого определяется сглаженное значение уровня ряда.
Если для исходного временного ряда
соответствующие сглаженные значения обозначить через 
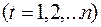

где 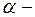


Используя, приведенное рекуррентное соотношение для всех уровней ряда, начиная с первого и кончая моментом времени 

здесь 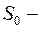
В практических задачах обработки экономических временных рядов рекомендуется выбирать величину параметра сглаживания в интервале от 0,1 до 0,3. Других точных рекомендаций для выбора оптимальной величины параметра 


Что касается начального параметра 



Указанный выше порядок выбора величины 
Методы анализа временных рядов: сглаживание
Временным рядом называется последовательность значений, изменяемых во времени. О некоторых простых, но эффективных подходах к работе с подобными последовательностями я попробую рассказать в данной статье. Примеров таких данных можно встретить очень много – котировки валют, объемы продаж, обращения клиентов, данные в различных прикладных науках (социология, метеорология, геология, наблюдения в физике) и многое другое.
Ряды являются распространенной и важной формой описания данных, так как позволяют наблюдать всю историю изменения интересующего нас значения. Это даёт нам возможность судить о «типичном» поведении величины и об отклонениях от такого поведения.
Передо мной встала задача выбрать набор данных, на котором можно было бы наглядно продемонстрировать особенности временных рядов. Я решил воспользоваться статистикой пассажиропотока на международных авиалиниях, поскольку этот набор данных весьма нагляден и стал своего рода стандартным (http://robjhyndman.com/tsdldata/data/airpass.dat, источник Time Series Data Library, R. J. Hyndman). Ряд описывает количество пассажиров международных авиалиний в месяц (в тысячах) за период с 1949 по 1960 года.
Поскольку у меня всегда под рукой Prognoz Platform, в которой есть интересный инструмент «Анализ временных рядов» для работы с рядами, я воспользуюсь именно им.
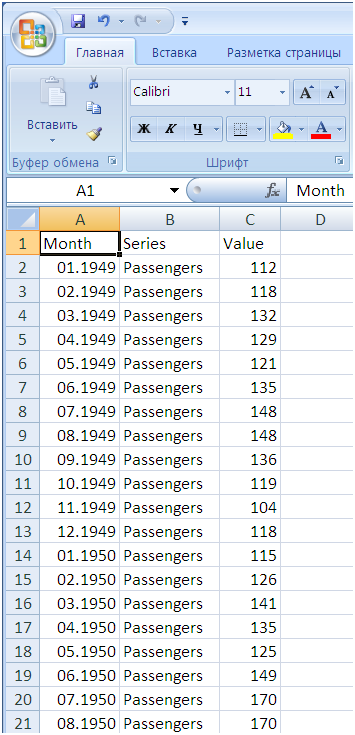
Перед импортом данных в файл нужно добавить столбец с датой, чтобы была привязка значений ко времени, и столбец с именем ряда для каждого наблюдения.
Ниже видно, как выглядит мой исходный файл, который я импортировал в Prognoz Platform с помощью мастера импорта непосредственно из инструмента анализа временных рядов.
Первое, что мы обычно делаем с временным рядом, это отображаем его на графике. Prognoz Platform позволяет построить график, просто «перетащив» ряд в рабочую книгу.
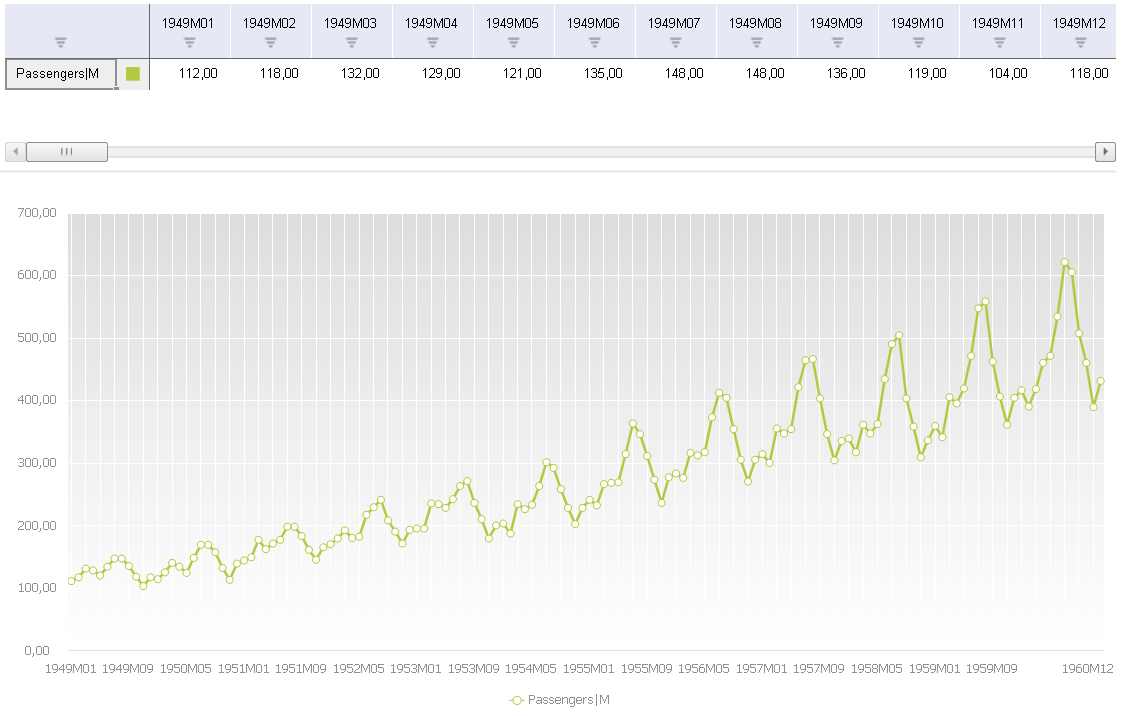
Символ ‘M’ в конце имени ряда означает, что ряд имеет месячную динамику (интервал между наблюдениями равен одному месяцу).
Уже из графика мы видим, что ряд демонстрирует две особенности:
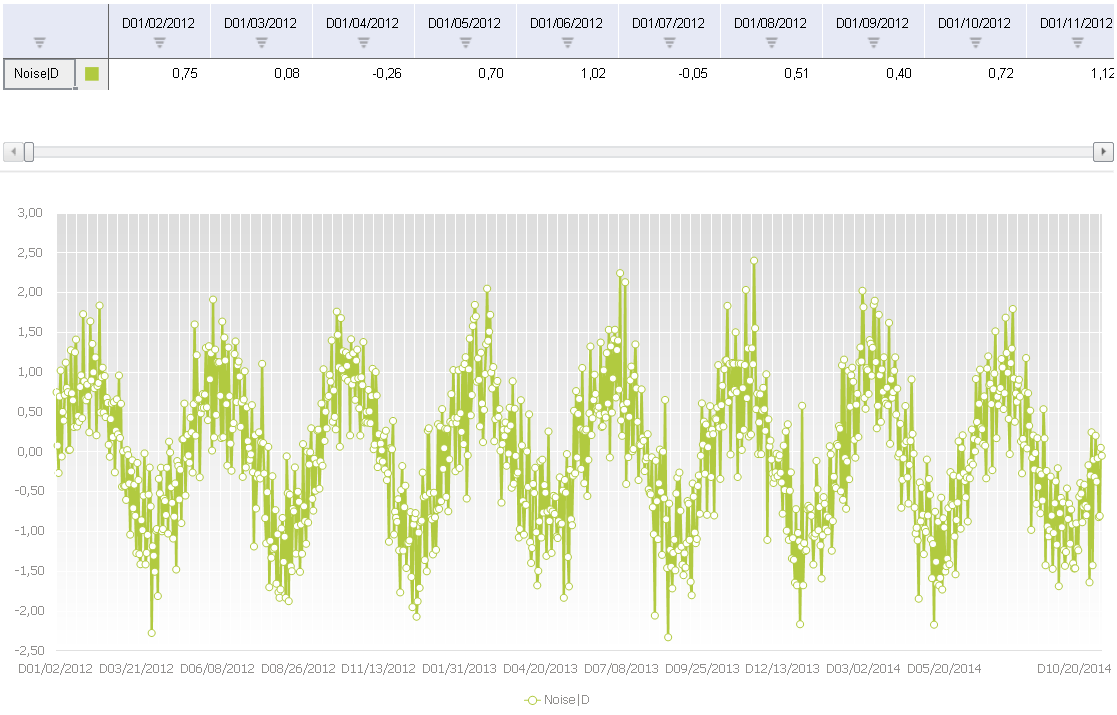
Наш ряд достаточно «аккуратный», однако часто встречаются ряды, которые помимо двух описанных выше характеристик демонстрируют ещё одну – наличие «шума», т.е. случайных вариаций в той или иной форме. Пример такого ряда можно увидеть на графике ниже. Это синусоидальный сигнал, смешанный со случайной величиной.
При анализе рядов нас интересует выявление их структуры и оценка всех основных компонентов – тренда, сезонности, шума и других особенностей, а также возможность строить прогнозы изменения величины в будущих периодах.
При работе с рядами наличие шума часто затрудняет анализ структуры ряда. Чтобы исключить его влияние и лучше увидеть структуру ряда, можно использовать методы сглаживания рядов.
Скользящее среднее
Самый простой метод сглаживания рядов – скользящее среднее. Идея заключается в том, что для любого нечётного количества точек последовательности ряда заменять центральную точку на среднее арифметическое остальных точек:
где xi – исходный ряд, si – сглаженный ряд.
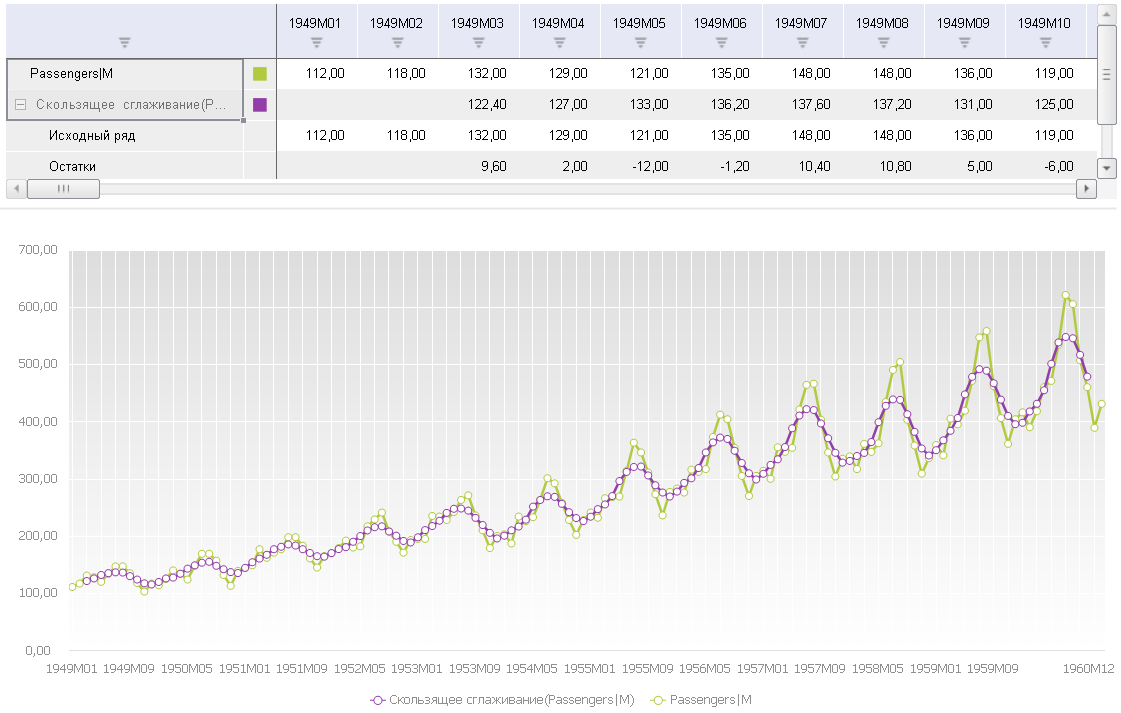
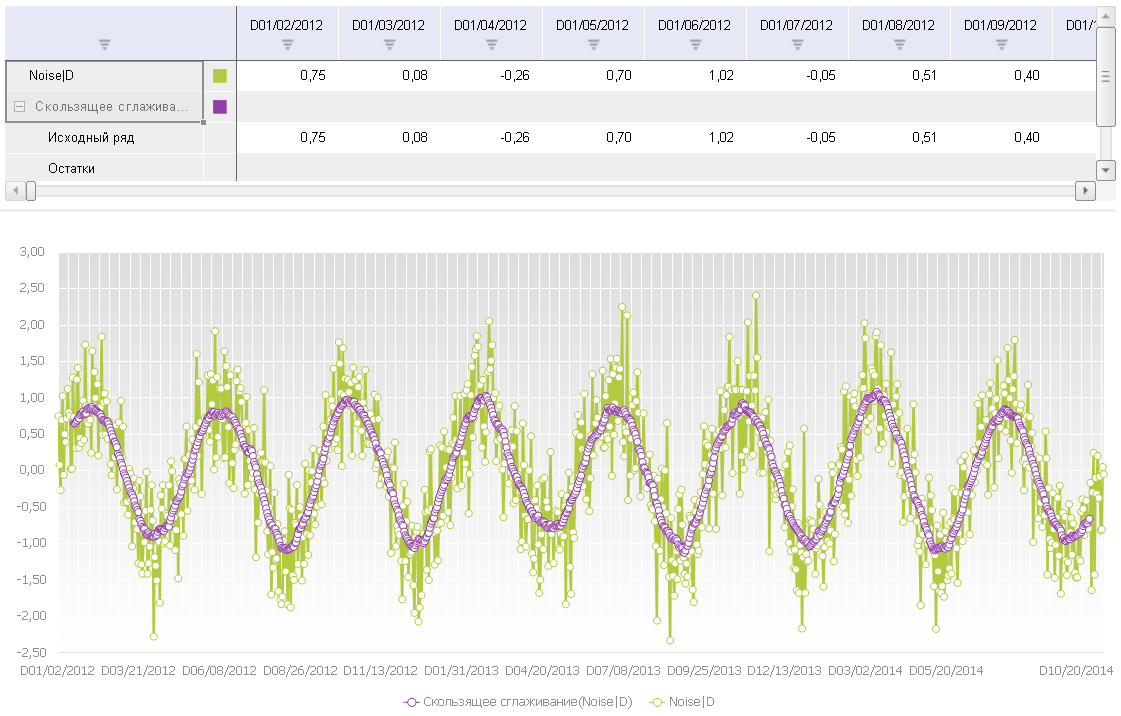
Ниже можно увидеть результат применения данного алгоритма к двум нашим рядам. Prognoz Platform по умолчанию предлагает использовать сглаживание с размером окна в 5 точек (k в нашей формуле выше будет равно 2). Обратите внимание, что сглаженный сигнал уже не так подвержен влиянию шума, однако вместе с шумом, естественно, пропадает и часть полезной информации о динамике ряда. Также видно, что у сглаженного ряда отсутствуют первые (и также последние) k точек. Это связано с тем, что сглаживание выполняется для центральной точки окна (в нашем случае для третьей точки), после чего окно сдвигается на одну точку, и вычисления повторяются. Для второго, случайного ряда, я использовал сглаживание с окном равным 30, чтобы лучше выявить структуру ряда, так как ряд «высокочастотный», точек очень много.
Метод скользящего среднего имеет определённые недостатки:
Экспоненциальное сглаживание
Более продвинутый метод сглаживания, который также можно использовать для прогнозирования – экспоненциальное сглаживание, также иногда называемое методом Хольта-Уинтерса (Holt-Winters) в честь имён его создателей.
Существует насколько вариантов данного метода:
Метод экспоненциального сглаживания вычисляет значения сглаженного ряда путём обновления значений, рассчитанных на предыдущем шаге, используя информацию с текущего шага. Информация с предыдущего и текущего шагов берётся с разными весами, которыми можно управлять.
В простейшем варианте одинарного сглаживания соотношение такое:
Параметр α определяет соотношение между несглаженным значением на текущем шаге и сглаженным значением с предыдущего шага. При α=1 мы будем брать только точки исходного ряда, т.е. никакого сглаживания не будет. При α=0 ряд мы будем брать только сглаженные значения с предыдущих шагов, т.е. ряд превратится в константу.
Чтобы понять, почему сглаживание называется экспоненциальным, нам нужно раскрыть соотношение рекурсивно:
Из соотношения видно, что все предыдущие значения ряда вносят вклад в текущее сглаженное значение, однако их вклад угасает экспоненциально за счёт роста степени параметра α.
Однако, если в данных есть тренд, простое сглаживание будет «отставать» от него (либо придётся брать значения α близкими к 1, но тогда сглаживание будет недостаточным). Нужно использовать двойное экспоненциальное сглаживание.
Двойное сглаживание использует уже два уравнения – одно уравнение оценивает тренд как разницу между текущим и предыдущим сглаженным значениями, потом сглаживает тренд простым сглаживанием. Второе уравнение выполняет сглаживание как в случае простого варианта, но во втором слагаемом используется сумма предыдущего сглаженного значения и тренда.
Тройное сглаживание включает ещё один компонент – сезонность, и использует ещё одно уравнение. При этом различаются два варианта сезонного компонента – аддитивный и мультипликативный. В первом случае амплитуда сезонного компонента постоянна и со временем не зависит от базовой амплитуды ряда. Во втором случае амплитуда меняется вместе с изменением базовой амплитуды ряда. Это как раз наш случай, как видно из графика. С ростом ряда амплитуда сезонных колебаний увеличивается.
Так как наш первый ряд имеет и тренд, и сезонность, я решил подобрать параметры тройного сглаживания для него. В Prognoz Platform это довольно просто сделать, потому что при обновлении значения параметра платформа сразу же перерисовывает график сглаженного ряда, и визуально можно сразу увидеть, насколько хорошо он описывает наш исходный ряд. Я остановился на следующих значениях:
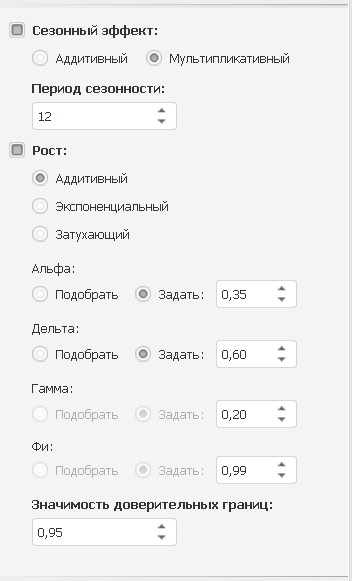
Как я вычислил период, мы рассмотрим в следующей статье о временных рядах.
Обычно в качестве первых приближений можно рассматривать значения между 0,2 и 0,4. Prognoz Platform также использует модель с дополнительным параметром ɸ, который дэмпфирует тренд так, что он приближается к константе в будущем. Для ɸ я взял значение 1, что соответствует обычной модели.
Также я сделал прогноз значений ряда данным методом на последние 2 года. На рисунке ниже я пометил точку начала прогноза, проведя через неё черту. Как видно, исходный ряд и сглаженный весьма неплохо совпадают, в том числе и на периоде прогнозирования – неплохо для такого простого метода!
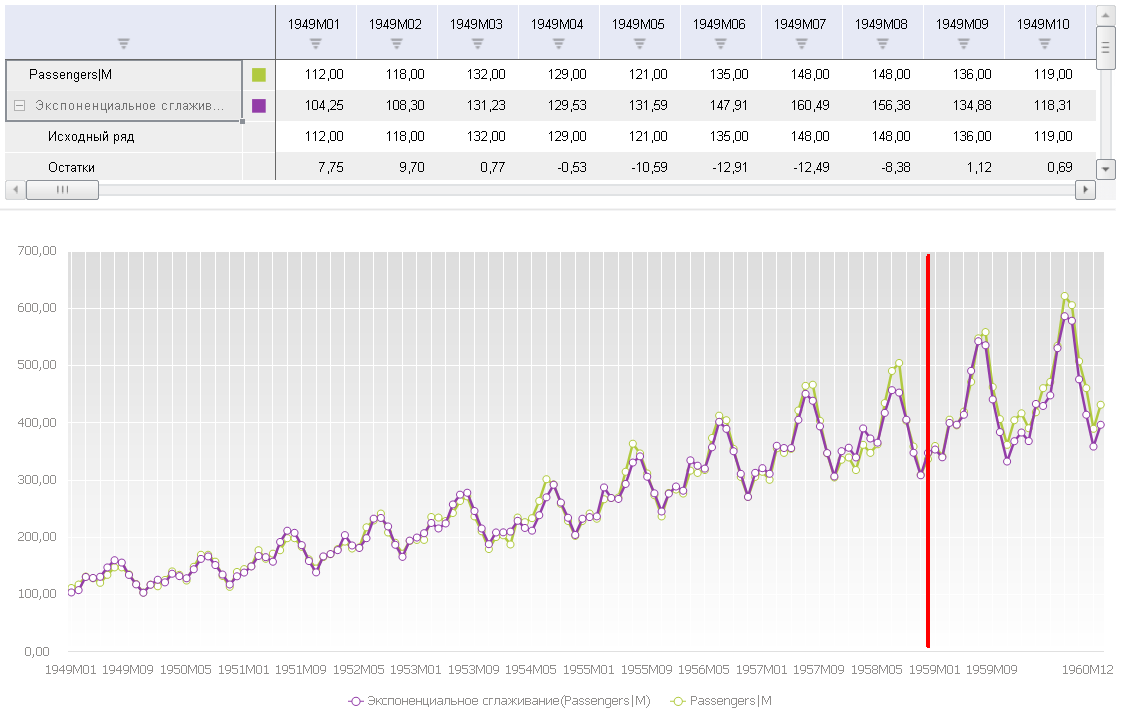
Prognoz Platform также позволяет автоматически подобрать оптимальные значения параметров, используя систематический поиск в пространстве значений параметров и минимизируя сумму квадратов отклонений сглаженного ряда от исходного.
Описанные методы весьма просты, их легко применять, и они являются хорошей отправной точкой для анализа структуры и прогнозирования временных рядов.
Методы анализа временных рядов: сглаживание
Временным рядом называется последовательность значений, изменяемых во времени. О некоторых простых, но эффективных подходах к работе с подобными последовательностями я попробую рассказать в данной статье.
Оглавление
Временным рядом называется последовательность значений, изменяемых во времени. О некоторых простых, но эффективных подходах к работе с подобными последовательностями я попробую рассказать в данной статье. Примеров таких данных можно встретить очень много – котировки валют, объемы продаж, обращения клиентов, данные в различных прикладных науках (социология, метеорология, геология, наблюдения в физике) и многое другое.
Ряды являются распространенной и важной формой описания данных, так как позволяют наблюдать всю историю изменения интересующего нас значения. Это даёт нам возможность судить о «типичном» поведении величины и об отклонениях от такого поведения.
Передо мной встала задача выбрать набор данных, на котором можно было бы наглядно продемонстрировать особенности временных рядов. Я решил воспользоваться статистикой пассажиропотока на международных авиалиниях, поскольку этот набор данных весьма нагляден и стал своего рода стандартным (http://robjhyndman.com/tsdldata/data/airpass.dat, источник Time Series Data Library, R. J. Hyndman). Ряд описывает количество пассажиров международных авиалиний в месяц (в тысячах) за период с 1949 по 1960 года.
Перед импортом данных в файл нужно добавить столбец с датой, чтобы была привязка значений ко времени, и столбец с именем ряда для каждого наблюдения. Ниже видно, как выглядит мой исходный файл, который я импортировал с помощью мастера импорта непосредственно из инструмента анализа временных рядов.
Первое, что мы обычно делаем с временным рядом, это отображаем его на графике. Prognoz Platform позволяет построить график, просто «перетащив» ряд в рабочую книгу.
Временной ряд на графике
Символ ‘M’ в конце имени ряда означает, что ряд имеет месячную динамику (интервал между наблюдениями равен одному месяцу).
Уже из графика мы видим, что ряд демонстрирует две особенности:
Наш ряд достаточно «аккуратный», однако часто встречаются ряды, которые помимо двух описанных выше характеристик демонстрируют ещё одну – наличие «шума», т.е. случайных вариаций в той или иной форме. Пример такого ряда можно увидеть на графике ниже. Это синусоидальный сигнал, смешанный со случайной величиной.
Временной ряд с шумом
При анализе рядов нас интересует выявление их структуры и оценка всех основных компонентов – тренда, сезонности, шума и других особенностей, а также возможность строить прогнозы изменения величины в будущих периодах.
При работе с рядами наличие шума часто затрудняет анализ структуры ряда. Чтобы исключить его влияние и лучше увидеть структуру ряда, можно использовать методы сглаживания рядов.
Скользящее среднее
Самый простой метод сглаживания рядов – скользящее среднее. Идея заключается в том, что для любого нечётного количества точек последовательности ряда заменять центральную точку на среднее арифметическое остальных точек:
Ниже можно увидеть результат применения данного алгоритма к двум нашим рядам. По умолчанию предлагаем использовать сглаживание с размером окна в 5 точек (k в нашей формуле выше будет равно 2). Обратите внимание, что сглаженный сигнал уже не так подвержен влиянию шума, однако вместе с шумом, естественно, пропадает и часть полезной информации о динамике ряда. Также видно, что у сглаженного ряда отсутствуют первые (и также последние) k точек. Это связано с тем, что сглаживание выполняется для центральной точки окна (в нашем случае для третьей точки), после чего окно сдвигается на одну точку, и вычисления повторяются. Для второго, случайного ряда, я использовал сглаживание с окном равным 30, чтобы лучше выявить структуру ряда, так как ряд «высокочастотный», точек очень много.
Метод скользящего среднего
Метод скользящего среднего имеет определённые недостатки:
Экспоненциальное сглаживание
Более продвинутый метод сглаживания, который также можно использовать для прогнозирования – экспоненциальное сглаживание, также иногда называемое методом Хольта-Уинтерса (Holt-Winters) в честь имён его создателей.
Существует насколько вариантов данного метода:
Метод экспоненциального сглаживания вычисляет значения сглаженного ряда путём обновления значений, рассчитанных на предыдущем шаге, используя информацию с текущего шага. Информация с предыдущего и текущего шагов берётся с разными весами, которыми можно управлять.
В простейшем варианте одинарного сглаживания соотношение такое:
Параметр α определяет соотношение между несглаженным значением на текущем шаге и сглаженным значением с предыдущего шага. При α=1 мы будем брать только точки исходного ряда, т.е. никакого сглаживания не будет. При α=0 ряд мы будем брать только сглаженные значения с предыдущих шагов, т.е. ряд превратится в константу.
Чтобы понять, почему сглаживание называется экспоненциальным, нам нужно раскрыть соотношение рекурсивно:
Из соотношения видно, что все предыдущие значения ряда вносят вклад в текущее сглаженное значение, однако их вклад угасает экспоненциально за счёт роста степени параметра α.
Однако, если в данных есть тренд, простое сглаживание будет «отставать» от него (либо придётся брать значения α близкими к 1, но тогда сглаживание будет недостаточным). Нужно использовать двойное экспоненциальное сглаживание.
Двойное сглаживание использует уже два уравнения – одно уравнение оценивает тренд как разницу между текущим и предыдущим сглаженным значениями, потом сглаживает тренд простым сглаживанием. Второе уравнение выполняет сглаживание как в случае простого варианта, но во втором слагаемом используется сумма предыдущего сглаженного значения и тренда.
Тройное сглаживание включает ещё один компонент – сезонность, и использует ещё одно уравнение. При этом различаются два варианта сезонного компонента – аддитивный и мультипликативный. В первом случае амплитуда сезонного компонента постоянна и со временем не зависит от базовой амплитуды ряда. Во втором случае амплитуда меняется вместе с изменением базовой амплитуды ряда. Это как раз наш случай, как видно из графика. С ростом ряда амплитуда сезонных колебаний увеличивается.
Так как наш первый ряд имеет и тренд, и сезонность, я решил подобрать параметры тройного сглаживания для него. Это довольно просто сделать, потому что при обновлении значения параметра платформа сразу же перерисовывает график сглаженного ряда, и визуально можно сразу увидеть, насколько хорошо он описывает наш исходный ряд. Я остановился на следующих значениях: