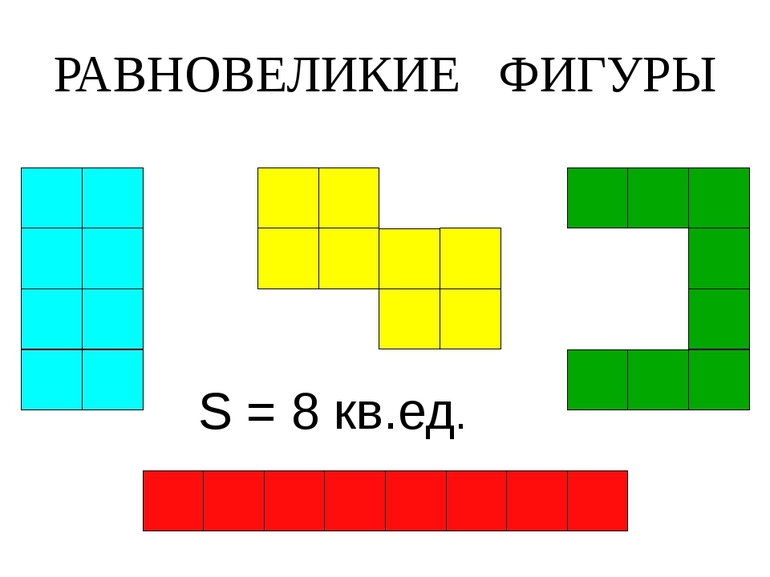
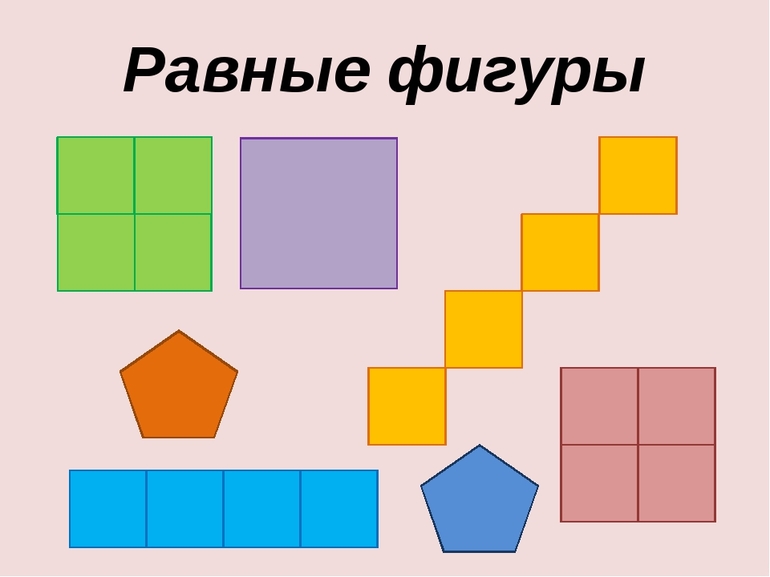
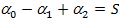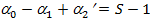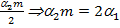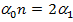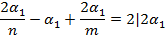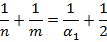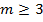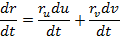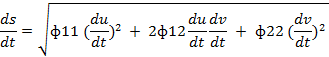какие многоугольники называются равновеликими и какие равносоставленными
Равновеликость и равносоставленность многоугольников



Определение[11.1]. Два многоугольника называются равновеликими, если они имеют равные площади.
Из определения следует, что равновеликость является отношением эквивалентности на множестве многоугольников, т. е. обладает свойствами рефлексивности, симметричности и транзитивности.
Определение[11.2]. Два многоугольника называются равносоставленными, если их можно разбить на одно и тоже число попарно равных многоугольников.
Очевидно, что равносоставленные многоугольники равновелики.
Теорема[11.1]. Равносоставленность многоугольников является отношением эквивалентности на множестве многоугольников.
Теорема[11.2]. (Бойяи—Гервина).Если два многоугольника равновелики, то они и равносоставлены.
(Доказательство этой теоремы см. в книге [?], c. 158—161).
Из приведенного выше утверждения и теоремы Бойяи—Гервина следует, что на множестве всех многоугольников отношение равновеликости совпадает с отношением равносоставленности.
Лекция № _4__.
Тема: исторический обзор геометрии
Основные вопросы, рассматриваемые на лекции:
1. Геометрия до Евклида.
3. V постулат Евклида.
4. Система аксиом Гильберта.
Краткое содержание лекционного материала
Исследовательская работа «Равновеликие и равно составленные фигуры»
Управление образования администрации Павловского района
Муниципальное бюджетное общеобразовательное учреждение
средняя школа №1 г. Павлово.
Научно-исследовательская работа на тему
«Равновеликие и равносоставленные фигуры».
Бочкарев Максим (14 лет)
Практическое применение равносоставленности…………………… 12-14
Рассмотрим две совершенно непохожие друг на друга фигуры. Казалось бы они совершенно разные, т.е. с точки зрения обывателя неравны. Но если эти фигуры вырезать из бумаги и разрезать одну из них на более мелкие фигуры, как показано на рисунке, то из этих частей можно сложить вторую фигуру.
Какая же связь этой игры с математикой? Во первых, в основе всей игры лежат геометрические фигуры, а во вторых при разрезании одной фигуры и составлении из нее другой фигуры используются свойства площадей данных фигур.
В 8 классе на уроках геометрии мы начали изучать площади многоугольников. При доказательстве форму площади параллелограмм и треугольника мы использовали способ перекраивания. Параллелограмм разрезанием и перекладыванием сводится к прямоугольнику, треугольник – к параллелограмму. Меня заинтересовали задачи, связанные с «разрезанием фигуры на части и перекладыванием этих частей». Так я впервые познакомился с понятиями «равновеликие фигуры и равносоставленные фигуры». Что же такое равновеликие и равносоставленные фигуры? Могут ли равные фигуры быть неравными и наоборот? Исследованием этих вопросов я занялся в своей работе.
При изучении теоремы Пифагора, я узнал, что теорему Пифагора можно доказывать различными способами, один из которых и использует равносоставленность и равновеликость.
Актуальность моего исследования состоит в том, что на основании понятий равносоставленности и перекраивания можно находить площади разных фигур, а также составлять головоломки.
Занимаясь данным исследованием, я попытался решить следующие задачи:
Изучить понятия равносоставленность и равновеликость и теоремы связанные с этими понятиями;
Рассмотреть способы перекраивания многоугольников при определении их площадей
Составить и решить некоторые головоломки на составление различных равновеликих фигур.
Найти практическое применение геометрических понятий равносоставленности и равновеликости
При исследовании различных многоугольников, я выдвинул гипотезу, что из любого многоугольника путем разрезания его определенным образом на конечное число частей можно составить любой другой равновеликий ему многоугольник.
А что же такое равновеликие и равносоставленные фигуры?
Какие треугольники называются равновеликими и какие равносоставленными? Нужно только определение.
Равновеликие и равносоставленные фигуры. Равновеликие фигуры — плоские (пространственные) фигуры одинаковой площади (объёма); равносоставленные фигуры — фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей. Обычно понятие равносоставленности применяется только к многоугольникам и многогранникам. Равносоставленные фигуры являются равновеликими. Венгерский математик Я. Больяй (1832) и немецкий математик П. Гервин (1833) доказали, что равновеликие многоугольники являются равносоставленными (теорема Больяй — Гервина). Поэтому разрезанием на части и перекладыванием их можно любой многоугольник превратить в равновеликий ему квадрат. Понятие равносоставленности лежит в основе «метода разбиения», применяемого для вычисления площадей многоугольников: параллелограмм «разрезанием и перекладыванием» сводят к прямоугольнику, треугольник — к параллелограмму, трапецию — к треугольнику. Эквивалентным понятию равносоставленности является понятие равнодополняемости, которое лежит в основе «метода дополнения», т. е. дополнения двух фигур равными частями так, чтобы получившиеся после такого дополнения фигуры были равны.
Равновеликие многогранники не всегда являются равносоставленными. (Поэтому при выводах формулы объёма треугольной пирамиды используют исчерпывания метод или иное завуалированное интегрирование, например Кавальери принцип. См. также Объём.) Так, например, куб и равновеликий ему правильный тетраэдр не являются равносоставленными — т. н. теорема Дена, доказанная немецким математиком М. Деном (1901) и составившая отрицательное решение третьей проблемы Гильберта. Для доказательства Ден построил некоторую систему аддитивных инвариантов, равенство которых необходимо для равносоставленности многогранников, и убедился, что среди его инвариантов есть такие, которые принимают разные значения для куба и равновеликого ему правильного тетраэдра. Эти работы были продолжены швейцарским математиком Х. Хадвигером и его учениками; в частности, Ж. П. Зидлер установил, что совпадение инвариантов Дена двух многогранников не только необходимо, но и достаточно для их равносоставленности.
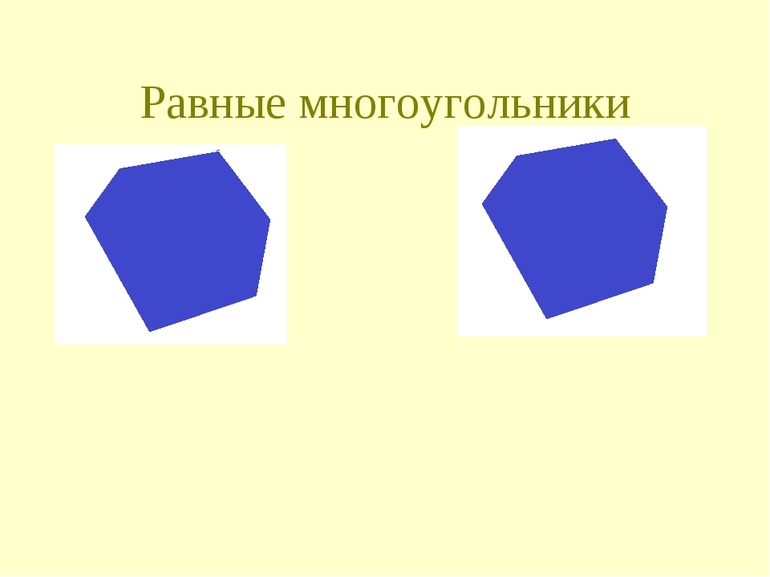
Равные многоугольники
По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:
Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.
Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».
В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.
Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.
Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.
Равность правильных фигур
Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».
Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.
Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.
Вычисление площади треугольника
Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.
Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.
То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.
Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.
Визуальный способ
Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.
Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.
Равносоставленность многоугольников
0:Два многоугольника будем называть равносоставленными, если их можно разрезать на одинаковое число соответственно равных многоугольников

Равновеликости многоугольников
0: Два многоугольника будем называть равновеликими, если каждому из них можно добавить одинаковое число соответственно равных многоугольников так, что получатся равносильные многоугольники.
Два равносоставленных многоугольника явл равновеликими.
Теорема:Параллелограммы с равными основаниями и равными высотами равновелики
Теорема: Если два многоугольника равносоставленны, то они равновеликими
Теорема Бояи – Гервина
Всякие два равновеликих многоугольника явл равносоставленными
Топологическое пространство. Топологическое многообразие. Эйлеровая характеристика двумерного многообразия. Теорема Эйлера для многогранников.
Топологическое простраство
Опр: Пусть Х-некоторое не пустое множество будет называть пространство-носитель и пусть 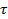
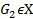
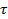
1) Объединение любой системы множеств из 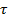
2) Пересечение конечного числа множеств из 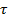
3) Пусть множество 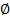
Множество Х вместе с заданной в нем топологией 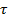
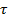
Элементы из Х называются точками. Множество 
1) 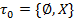
2) 
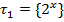
3) Каждое метрическое пространство является топологическим пространством.
Многообразие
Пусть (X, 
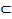
k-мерным топологическим многообразием (или просто k-мерным многообразием) называют отделимое топологическое пространство (X, 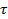
В топологии доказывают, что число k (размерность многообразия) является топологическим инвариантом, т. е. не меняется при любых гомеоморфизмах пространства
Клеточное разложение.
Множество всех краевых точек называется краем многообразия (X, У).
Назовем клеткой любое многообразие с краем, гомеоморфное выпуклому многоугольнику. При этом предполагается, что для данной клетки этот гомеоморфизм фиксирован. Образ вершины многоугольника при этом гомеоморфизме мы назовем вершиной клетки, а образ стороны многоугольника — стороной клетки.
Мы скажем, что двумерное многообразие F разложено на конечное множество клеток F1, F2,. Fn, если выполняются два условия:
1.эти клетки образуют покрытие многообразия F;
2.пересечение любых двух клеток Fi и Fj(i 
Пусть К — клеточное разложение двумерного многообразия. Точка х 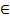
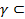
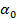
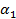
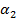
Число 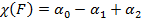
В топологических преобразованиях меняются многие свойства фигур (длина, площади, прямолинейность). Некоторые более сильные сохраняются.
Теорема Эйлера: Если 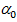


Док-во: пусть многогранник внутри пустой. Пусть
Одну грань вырежем останется поверхность ее растянем на плоскости.
Число вершин и ребер не изменилось, а граней станет на 1 меньше.
Трианвумеруем (величина не меняется) диагоналями разбиваем на треугольники. 2 типа треугольника: 1. С границей одной стороной; 2) с границей 2 сторонами.
Если отрежем треугольник 1-го типа, число граней уменьшится на 1, вершин на 1.
Если 2-го типа – вершин и граней уменьшится на 1, ребер на 2.
Теорема Эйлера позволяет установить если правильные многогранники.
Существует 5 типов:
Многогранник называется правильным если в гранях его лежит равные правильные многоугольники, а в вершине правильные n-гранные углы, m-угольники в гранях.


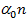
1) 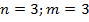
2) 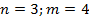
3) 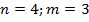
4) 
5) 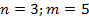
12. Линии и поверхности в Е3. Первая основная квадратичная форма поверхности и её приложения.
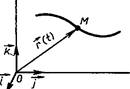
векторную функцию r(t) скалярного аргумента t, определенную в промежутке J. Эта функция имеет координаты x(t), y(t),z(t) в базисе i,j, k. Это значит, что r(t) = x(t)+ у (t)J+ z(t)k, причем x(t), y(t), z(t) — координаты точки М в момент времени t.
Простейшими линиями в пространстве Ез назовем любую прямую, отрезок и луч. Фигура 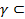
Если в пространстве Ез задана прямоугольная система координат Oijk, то элементарная линия 
Уравнения называются параметрическими уравнениями данной линии.
Линией (или кривой) называется фигура, которую можно покрыть конечным или счетным множеством элементарных линий.
Будем называть простейшей поверхностью в пространствеE3 любую из следующих фигур: плоскость, замкнутую полуплоскость, квадрат.
Элементарной поверхностью называется фигура, гомеоморфная какой-либо из простейших поверхностей.
Зададим в пространстве прямоугольную систему координат
Oijk и рассмотрим тот гомеоморфизм f :G->Fo, который переводит область G в элементарную поверхность F0. Если точка (u, v) 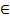
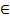
Пусть F0 — элементарная поверхность, заданная параметрическими уравнениями. Поверхность F0 называется гладкой класса C k (k — натуральное число), если правые части уравнений являются функциями, имеющими в области G непрерывные частные производные до порядка k включительно.
Дифференциал векторной функции r(u, v) в произвольной точке имеет вид dr = rudu + rvdv. Отсюда следует, что (dr) 2 = ф11 (du) 2 + ф12dudv + ф21 dvdu + ф22 (dv) 2
Квадратичная форма ф11 (du) 2 + 2ф12dudv + ф22 (dv) 2 называется первой квадратичной формой поверхности Fo или ее линейным элементом.
1.Квадратичная форма положительно определенная, так как если du и dv не обращаются в нуль одновременно
2.Касательное векторное подпространство Тм к поверхности F0 в ее точке М является двумерным евклидовым векторным пространством.
Рассмотрим на поверхности Fо гладкую линию 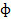

Так как 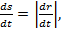
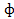
Отсюда следует, что
(ds) 2 = ф11 (du) 2 + 2ф12dudv + ф22 (dv) 2
Таким образом, значение первой квадратичной формы поверхности представляет собой квадрат дифференциала длины дуги гладкой линии, лежащей на поверхности, при бесконечно малом смещении точки вдоль этой линии.
Получаем формулу для вычисления длины дуги линии ф с концами в точках M1(t1) и М2(t2), где t1