какие множества чисел не пересекаются
Тест с ответами: “Теория множеств”
1. Множество, не содержащее ни одного элемента, называется:
а) пустым +
б) конечным
в) нулевым
2. Число всех подмножеств множества K= <7,9,11,13,15,17,19>равно:
а) 182
б) 128 +
в) 88
3. Множество решений уравнения записывается:
а) <-2,3>
б) (2;-3)
в) <2,-3>+
4. Мощность множества B= <0,1,2,3,5,9,27,38>равна:
а) 8 +
б) 18
в) 4
5. Правильная запись предложения «Y – множество действительных чисел, больших 3» – это:
а) Y=
б) Y=
в) Y=
7. Не пересекаются множества чисел:
а) простых и четных
б) простых и нечетных
в) простых и составных +
8. Пересечение множеств равносторонних и прямоугольных треугольников – это множество треугольников:
а) пустое множество +
б) равнобедренных
в) прямоугольных
9. Пересечение множеств прямоугольников и ромбов – это множество:
а) параллелограммов
б) прямоугольников
в) квадратов +
10. Пересекаются множества чисел:
а) четных и нечетных
б) простых и четных +
в) простых и составных
11. Мощность множества A= <-3,0,2,5,13>равна:
а) 5 +
б) 15
в) 2
14. Множество решений неравенства записывается в виде:
а) (1;0)
б) (0;1)
в) (-1;0) +
15. Число всех подмножеств множества E= <5,10,15,20,25,30>равно:
а) 64 +
б) 46
в) 164
16. Множество решений уравнения записывается:
а) <-4,3>
б) <-3,4>+
в) (3;-4)
17. Математический символ Ø обозначает:
а) нулевое множество
б) бесконечное множество
в) пустое множество +
18. Существует множество без элементов:
а) нет
б) да +
в) в любом множестве не менее 1 элемента
19. Если все элементы множества А входят в множество В, то можно сказать, что:
а) А – образ множества В
б) В – прообраз множества
в) А – подмножество В +
20. Множество, состоящее из определенного числа конкретных элементов, называется:
а) определенным
б) конкретным +
в) конечным
21. Если можно найти разность двух множеств, то можно найти их:
а) объединение +
б) произведение
в) сумму
22. При обозначении множеств используют:
а) только круглые скобки
б) только фигурные скобки +
в) иногда круглые, иногда фигурные, иногда одновременно оба вида скобок
23. При операциях на числовых множествах за универсальное множество берут:
а) все целые числа
б) только множество натуральных чисел
в) всё множество действительных чисел +
24. Как можно изобразить множество графически:
а) частью координатной плоскости
б) диаграммами Эйлера-Венна +
в) интервалом на числовой оси
25. При пересечении двух множеств получаем третье множество, которое:
а) всегда состоит из одного элемента
б) всегда не содержит элементов
в) может состоять из одного элемента +
26. Множества обозначаются:
а) малыми латинскими буквами
б) большими латинскими буквами +
в) кириллицей
27. Какой операции над множествами соответствует выражение:
“Элемент, принадлежащий полученному множеству, принадлежит множеству А И множеству В.”:
а) пересечение множеств +
б) перечисление множеств
в) дополнение множества
28. Какой операции над множествами соответствует выражение:
“Элемент, принадлежащий полученному множеству, принадлежит множеству А ИЛИ множеству В.”:
а) пересечение множеств
б) перечисление множеств
в) объединение множеств +
29. Если элемент x принадлежит множеству X, то записывают:
а) x ∈ Х +
б) x | X
в) x ⊂ X
30. Если множество А является частью множества В, то записывают:
а) A | B
б) А ⊂ В +
в) А ∈ B
Тест по теме «Элементы теории множеств»
по теме «Элементы теории множеств»
1.Множество, не содержащее ни одного элемента, называется:
1) нулевым; 2) пустым ; 3) бесконечным; 4) безэлементным.
2.Множество решений уравнения записывается:
3.Множество решений неравенства записывается в виде:
5. Для множеств A = <-3,5,8>и B = <1,5,9>справедливы утверждения:
1) AB=; 2) A=B; 3) A\B= ; 4) AB=A.
6.Не пересекаются множества чисел:
1) простых и нечетных;
2) простых и четных;
3) простых и составных ;
4) составных и нечетных.
7.Пересечение множеств прямоугольников и ромбов – это множество
1) квадратов ; 2) параллелограммов; 3) прямоугольников; 4) пустое множество.
8.Мощность множества A= <-3,0,2,5,13>равна:
9.Декартово произведение множеств A = <-1,2>и B = <0,-3>– это
10.Число всех подмножеств множества E = <5,10,15,20,25,30>равно
1) 6; 2) 30; 3) 32; 4) 64.
по теме «Элементы теории множеств»
1.Математический символ обозначает:
1) нулевое множество; 2) бесконечное множество; 3) пустое множество ; 4) безэлементное множество.
2.Множество решений уравнения записывается:
3.Множество решений неравенства записывается в виде:
5. Для множеств A = <-1,7,9>и B = <1,3,8>справедливы утверждения:
6. Пересекаются множества чисел:
1) четных и нечетных;
2) простых и составных;
3) простых и четных ;
4) положительных и отрицательных.
7. Пересечение множеств равносторонних и прямоугольных треугольников – это множество треугольников:
1) равнобедренных; 2) пустое множество ; 3) разносторонних; 4) прямоугольных.
8.Мощность множества B = <0,1,2,3,5,9,27,38>равна:
9.Декартово произведение множеств A = <0,-3>и B = <-1,2>– это
10.Число всех подмножеств множества K = <7,9,11,13,15,17,19>равно
1) 7; 2) 19; 3) 120; 4) 128.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Тест может быть использован учителями (преподавателями) для контроля знаний и умений обучающихся после изучения темы «Элементы теории множеств». Тест содержит два варианта, каждый из которых включает 10 вопросов. При составлении теста использовалось современное учебное пособие для СПО «Математика. Тесты» Кучер Т.П. (2019 год издания).
Номер материала: ДБ-784180
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Минпросвещения будет стремиться к унификации школьных учебников в России
Время чтения: 1 минута
В проекте КоАП отказались от штрафов для школ
Время чтения: 2 минуты
Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года
Время чтения: 1 минута
Российские адвокаты бесплатно проконсультируют детей 19 ноября
Время чтения: 2 минуты
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
Шойгу предложил включить географию в число вступительных экзаменов в вузы
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Пересечение, объединение и разность множеств
Пересечение множеств
Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:
Объединение множеств
Объединением – множеств A и B называют множество, содержащее те и только те элементы, которые входят хотя бы в одно из множеств, A или B:
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:
При рассмотрении целочисленных задач, универсум – это множество целых чисел.
При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Свойства операций пересечения и объединения
$(A \cap B) \cap C = A \cap (B \cap C)$
$(A \cup B) \cap C = (A \cap C) \cup (B \cap C)$
Взаимодействие с отрицанием, пустым множеством и универсумом
$A \cap \varnothing = \varnothing$
$A \cup \varnothing = A$
Разность множеств
Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A \cup B) = n(A)+ n(B)-n(A \cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.
Примеры
Пример 1. Найдите пересечение данных множеств:
Пересечение и объединение множеств
Урок 13. Информатика 3 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Пересечение и объединение множеств»
Вы знаете, ученик третьего класса Максим очень хотел объяснить вам эту тему, но немного приболел и прийти сегодня не смог. Но, благодаря Интернету, мы можем с ним связаться.
̶ Здравствуй Максим!
̶ Здравствуйте! Проверьте, чтобы ваши соседи по парте были готовы к уроку. И мы начинаем.
Прослушайте название пар множеств и попытайтесь заметить, что повторяется в каждой паре.
Животные и герои мультфильмов;
Материки и части света;
Ну, что заметили? Конечно, повторялся слово «и».
Если в названии множества есть союз «И», то каждый его элемент должен находиться на пересечении двух множеств, т.е. находиться одновременно в двух множествах. Другими словами мы можем сказать, что пересечение множеств – это их общая часть.
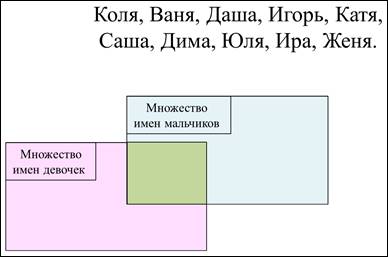
Необходимо разместить элементы по своим множествам.
Давайте посмотрим, что за элементы. Так это имена мальчиков и девочек: Коля, Ваня, Даша, Игорь, Катя, Саша, Дима, Юля, Ира, Женя. Будем размещать имена мальчиков в синий прямоугольник, а девочек – в розовый. Ага! Так ведь Сашей и Женей могут звать как мальчиков, так и девочек. Значит, эти два имени будут находиться сразу в двух множествах, т.е. на пересечении двух множеств.
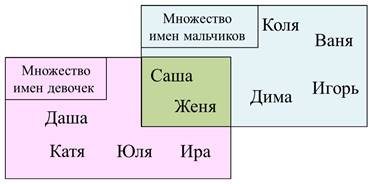
Итак, Коля, Ваня – это мальчики, помещаем эти элементы во множество имён мальчиков. Даша – имя девочки, помещаем в розовый прямоугольник, где находятся имена девочек. Игорь – имя мальчика, Катя – имя девочки. Саша, так могут звать и мальчика, и девочку, значит, этот элемент будет находиться на пересечении двух множеств. Дима – элемент из множества имён мальчиков. Юля, Ира, конечно элементы из множества имён девочек. И последнее имя, Женя, это имя могут иметь как девочки, так и мальчики. Значит, этот элемент будет находиться на пересечении двух множеств.
Теперь все имена находятся в своих множествах.
А сейчас я прочитаю названия ещё нескольких пар множеств, а вы попытайтесь заметить, что повторяется в этих парах.
Полевые или садовые цветы;
Попугаи или морские свинки;
Рабочие или выходные дни.
Заметили, что повторялось в парах множеств? Конечно, это слово «или».
Посмотрите ещё раз на названия множеств.
Например, яблоки или груши. А ведь эти множества можно объединить в одно с общим названием «фрукты» и все элементы будут располагаться в одном новом множестве.
Попугаи или морские свинки. Их можно объединить во множество с названием
«домашние животные» и все попугаи, и все морские свинки будут находиться в новом множестве.
Значит, если в названии множества есть слово «или», то его элемент может находиться в любом множестве и тогда происходит объединение множеств, т.е. эти множества объединяются.
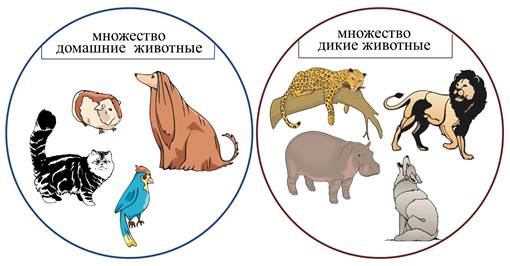
Давайте рассмотрим два множества: домашние животные, дикие животные.
Множество домашние животные содержат следующие элементы: собака, кошка, морская свинка, попугай.
Множество дикие животные состоит из следующих элементов: бегемот, леопард, волк, лев.
Какой общий признак у элементов этих двух множеств? Элементы каждого из них относятся с животному миру. Значит, можно, объединив эти множества, создать новое множество под названием животные. Теперь все элементы находятся в одном множестве.
А теперь, конечно, задание.
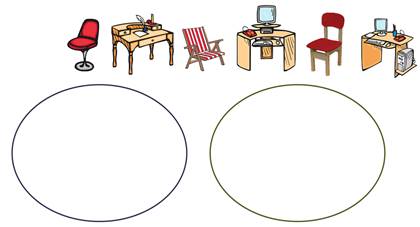
Распределить элементы по множествам, объединить их и придумать название для нового множества.
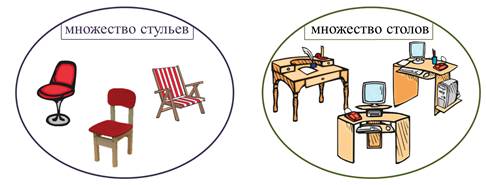
Итак, смотрим на элементы. Ага, у нас два множества: множество стульев и множество столов. Распределяем элементы по множествам. Все элементы стулья во множество стульев, а все элементы столы во множество столов.
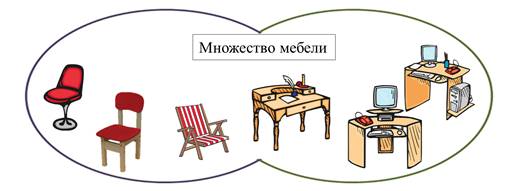
Объединяем множества. Какое название будет у нашего нового множества? Множество мебели.
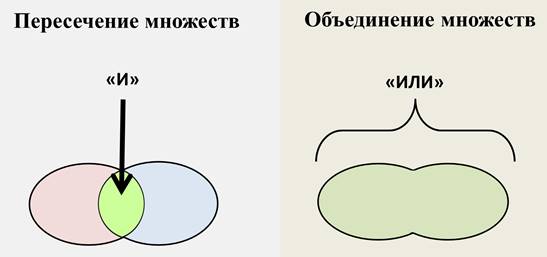
Давайте ещё раз определим разницу между пересечением и объединением множеств.
Если в названии множества есть слово «И», то это пересечение, и каждый элемент должен находиться на пересечении двух множеств.
Если в названии множества есть слово «или», то его элемент может находиться в любо области объединённых множеств.
Я надеюсь, что вы поняли разницу между пересечением и объединением множеств. А давайте проверим?
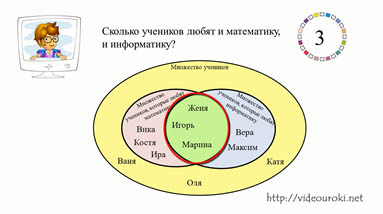
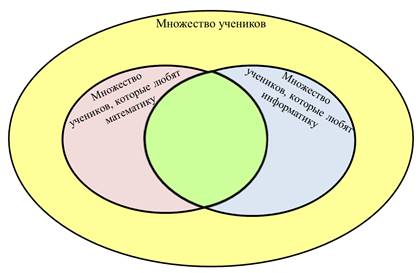
Итак, перед вами рисунок с тремя множествами.
Множество учеников, которые любят математику, множество учеников, которые любят информатику и множество всех учеников. Но, среди учеников есть и такие, которые любят и математику и информатику. Значит, эти два множества пересекаются и одновременно они являются подмножеством множества всех учеников. А теперь появляются элементы во множествах.
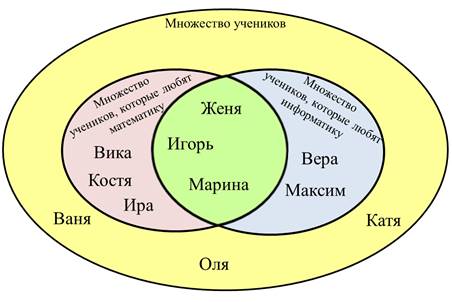
Используя полученные знания сегодня на уроке, будем отвечать на вопросы. А все ответы хранятся на этом рисунке, главное внимательно слушать вопросы и внимательно смотреть на рисунок.
Сколько учеников любят математику? Считаем их во множестве учеников, которые любят математику, и не забываем посчитать тех учеников, которые находятся на пересечении двух множеств учеников, которые любят и математику, и информатику. Считаем. Их шесть.
Сколько учеников любят информатику? Считаем их во множестве учеников, которые любят информатику и опять считаем тех учеников, которые находятся на пересечении двух множеств. Считаем. Их пять.
Сколько учеников любят и математику, и информатику? Будем считать тех учеников, которые находятся на пересечении двух множеств. Их три.
Сколько учеников любят или математику или информатику? Если используется слово «или», значит элементы находятся в любом месте множеств за исключением любителей двух предметов сразу. Значит, считаем учеников и в первом множестве и во втором, но не включаем тех, кто находится в пересечении. Их пять.
Сколько учеников любят только математику? Любят математику только те, которые находятся во множестве учеников, которые любят математику. Ученики, которые находятся на пересечении двух множеств, сюда относится не будут, т.к. они любят и математику, и информатику. Итак, считаем и получается, что 3 ученика любят только математику.
Сколько учеников любят только информатику? Опять, учеников, которые находятся на пересечении двух множеств, считать не будем. Любителей информатики двое.
Сколько учеников не любят математику? Надо посчитать их во множестве учеников, которые любят информатику, кроме тех, которые находятся на пересечении множеств, т.к. эти ученики любят информатику и математику. А так же надо посчитать тех учеников, которые находятся во множестве всех учеников, т.к. они не любят математику. Их всего 5.
Всем спасибо за отличную работу. Теперь я точно понял, что хочу быть учителем!
Тебе спасибо, Максим. Тему объяснил хорошо. До свидания! А мы ещё сделаем выводы.
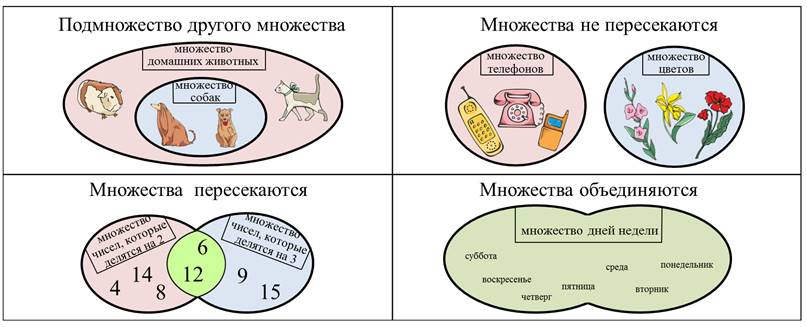
Множество – это объединение некоторых объектов (элементов) в группу по определённым признакам.
Множество может быть подмножеством другого множества. Например: множество собак является подмножеством множества домашние животные.
Множества могут пересекаться. Например: множество чисел, которые делятся на 2, и множество чисел, которые делятся на 3, пересекаются, т.к. числа, например, 6 и 12 делится и на 2, и на 3.
Множества могут и не пересекаться. Например: множество телефонов и множество цветов.
И множества могут объединяться. Например: множество рабочих дней недели и множество выходных можно объединить в одно множество дней недели.
Выводы сделаны, и я желаю вам успехов при выполнении заданий!