какие модели характеризуют индивидуальные особенности моделируемого объекта
(модуль) Теория анализа и статистика
Заочное отделение ФЭМ СПбГТИ(ТУ)
Модуль по Теории анализа и статистике тестирование онлайн, ответы на тесты по (модуль) Теории анализа и статистики. Выполняем тестирование он-лайн для студентов ФЭМ Технологического института по (модуль) Теории анализа и статистики. Стоимость прохождения он-лайн тестов за весь курс уточняйте при заказе (присылаете логин и пароль от личного кабинета, мы сообщим Вам стоимость).
Теория анализа и статистика (модуль)
ТАС. Лекция 1. Моделирование в экономике и его использование в развитии и формализации экономической теории
ТАС. Лекция 2. Математическая модель и ее основные элементы. Экзогенные и эндогенные переменные, параметры
ТАС. Лекция 3. Основные типы моделей в математической экономике
ТАС. Лекция 4. Линейные модели экономики. Основные понятия, терминология. Планирование выпуска на уровне отраслей
ТАС. Лекция 5. Модель Леонтьева «затраты-выпуск». Балансовый анализ. Планирование производства в динамике
ТАС. Лекция 6. Модель расширяющейся экономики Неймана. Магистральные траектории в линейных моделях экономики
ТАС. Лекция 7. Линейная модель обмена (модель международной торговли)
ТАС. Лекция 8. Функции и графики в экономическом моделировании. Понятие функциональной зависимости
ТАС. Промежуточный тест 1
ТАС. Лекция 9. Экономические задачи, решаемые методами дифференциального исчисления. Приращение величины, аргумента, функции
ТАС. Лекция 10. Понятие производной, ее геометрический и экономический смысл. Правила дифференцирования
ТАС. Лекция 11. Абсолютные и относительные величины в экономическом анализе
ТАС. Лекция 12. Соотношения между суммарными, средними и маржинальными (предельными) величинами
ТАС. Лекция 13. Функции суммарного, среднего и предельного дохода и издержек
ТАС. Лекция 14. Функция полезности. Задача потребительского выбора. Общая модель потребительского выбора
ТАС. Лекция 15. Понятие производственной функции. Формальные свойства производственных функций
ТАС. Лекция 16. Предельные (маржинальные) и средние значения производственной функции
ТАС. Лекция 17. Производственные функции в темповой записи. Эластичность замещения факторов. Производственная функция CES
ТАС. Лекция 18. Показатели экономической динамики. Понятие динамического равновесия в экономике
ТАС. Промежуточный тест 2
ТАС. Лекция 19. Примеры моделей экономической динамики. Модели макроэкономической динамики
ТАС. Лекция 20. Введение случайного компонента в экономическую модель. Стохастические модели и статистические данные
ТАС. Лекция 21. Экономические данные: перекрестные данные (cross-section data) и временные ряды (time series)
ТАС. Лекция 22. Построение теоретических моделей на основе экономических данных: статистические методы
ТАС. Лекция 23. Понятие генеральной совокупности и выборки (выборочной совокупности)
ТАС. Лекция 24. Дискретные и непрерывные случайные величины, их основные статистические характеристики
ТАС. Лекция 25. Выборочное наблюдение. Основные алгоритмы решения задач выборочного наблюдения
ТАС. Лекция 26. Индексная методология в экономической статистике
ТАС. Итоговый тест
ТАС. Варианты и указания для контрольной работы
ТАС. Контрольная работа Задание
ТАС. Доп. испытания
В перечень условных обозначений при разработке структурной экономико-математической модели входят:
1. только индексация
2. индексация, неизвестные и известные величины
3. неизвестные и известные величины
Какая группа функций преимущественно применяется в экономико-математическом моделировании?
— __________ функции.
Ответ:
Какие группы неизвестных величин может содержать экономико-математическая модель:
1. основные, вспомогательные и косвенные
2. основные, дополнительные и вспомогательные
3. основные, дополнительные и косвенные
Какие модели характеризуют индивидуальные особенности моделируемого объекта:
1. структурные и развернутые
2. развернутые
3. структурные
Критерий оптимальности – это:
1. математическое выражение, описывающее целевую функцию
2. экономическая категория, характеризующая цель решения задачи
3. экономический показатель, характеризующий особенности функционирования экономики
Критерий оптимальности при построении модели формализуется в виде:
1. целевой функции
2. ограничений задачи
3. сводных чисел
Модель межотраслевого баланса Леонтьева является:
1. моделью, учитывающей затраты на увеличение производства
2. статической моделью
3. динамической моделью
4. моделью, учитывающей внешнеэкономические затраты
Ограничения задачи подразделяются на:
1. основные, дополнительные и вспомогательные
2. главные и второстепенные
3. основные и дополнительные
При использовании условных обозначений необходимо соблюдать принцип:
1. значимости, экономичности и запоминаемости
2. значимости, последовательности, экономичности
3. последовательности, экономичности и запоминаемости
Экономико-математическая модель описывает:
1. лишь незначительную часть
2. все особенности функционирования объекта
3. только наиболее существенные
Для заказа он-лайн тестирования по теории анализа и статистики присылайте свой логин и пароль.
Понятие модели и моделирования
Сам по себе процесс моделирования в полной мере не формализован, большая роль в этом принадлежит опыту инженера. Но, тем не менее, рассматриваемый в теме процесс создания модели в виде шести этапов может стать основой для начинающих и с накоплением опыта может быть индивидуализирован.
1.1. Общее определение модели
Однако во многих случаях натурный эксперимент невозможен.
Например, наиболее полную оценку новому виду вооружения и способам его применения может дать война. Но не будет ли это слишком поздно?
Натурный эксперимент с новой конструкцией самолета может вызвать гибель экипажа.
Натурное исследование нового лекарства опасно для жизни человека.
Натурный эксперимент с элементами космических станций также может вызвать гибель людей.
Время подготовки натурного эксперимента и проведение мероприятий по обеспечению безопасности часто значительно превосходят время самого эксперимента. Многие испытания, близкие к граничным условиям, могут протекать настолько бурно, что возможны аварии и разрушения части или всего объекта.
Из сказанного следует, что натурный эксперимент необходим, но в то же время невозможен либо нецелесообразен.
Выход из этого противоречия есть и называется он » моделирование «.
Моделирование, в-третьих, это перенос полученных на модели сведений на оригинал или, иначе, приписывание свойств модели оригиналу. Чтобы такой перенос был оправдан, между моделью и оригиналом должно быть сходство, подобие.
Остановимся на основных целях моделирования.
Часто модель создается для применения в качестве средства обучения: модели-тренажеры, стенды, учения, деловые игры и т. п.
Гениальный полководец А. В. Суворов перед атакой крепости Измаил тренировал солдат на модели измаильской крепостной стены, построенной специально в тылу.
Наш знаменитый механик-самоучка И. П. Кулибин (1735-1818) создал модель одноарочного деревянного моста через р. Неву, а также ряд металлических моделей мостов. Они были полностью технически обоснованы и получили высокую оценку российскими академиками Л. Эйлером и Д. Бернулли. К сожалению, ни один из этих мостов не был построен.
1.2. Классификация моделей и моделирования
Каждая модель создается для конкретной цели и, следовательно, уникальна. Однако наличие общих черт позволяет сгруппировать все их многообразие в отдельные классы, что облегчает их разработку и изучение. В теории рассматривается много признаков классификации, и их количество не установилось. Тем не менее, наиболее актуальны следующие признаки классификации:
1.2.1. Классификация моделей и моделирования по признаку «характер моделируемой стороны объекта»
В соответствии с этим признаком модели могут быть:
Функциональные модели отображают только поведение, функцию моделируемого объекта. В этом случае моделируемый объект рассматривается как «черный ящик», имеющий входы и выходы. Физическая сущность объекта, природа протекающих в нем процессов, структура объекта остаются вне внимания исследователя, хотя бы потому, что неизвестны. При функциональном моделировании эксперимент состоит в наблюдении за выходом моделируемого объекта при искусственном или естественном изменении входных воздействий. По этим данным и строится модель поведения в виде некоторой математической функции.
1.2.2. Классификация моделей и моделирования по признаку «характер процессов, протекающих в объекте»
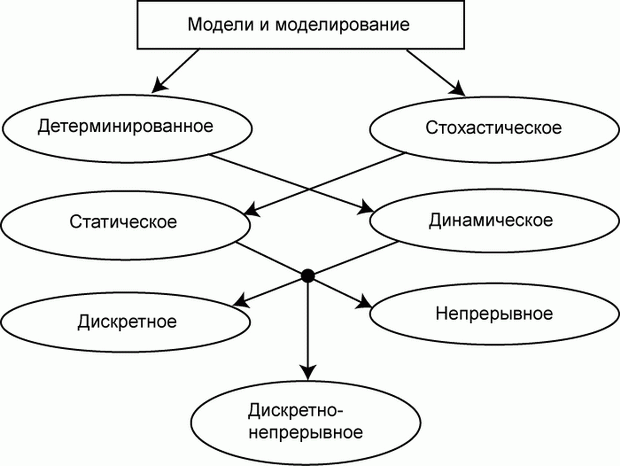
По этому признаку модели могут быть детерминированными или стохастическими, статическими или динамическими, дискретными или непрерывными или дискретно-непрерывными.
Детерминированные модели отображают процессы, в которых отсутствуют случайные воздействия.
Стохастические модели отображают вероятностные процессы и события.
Статические модели служат для описания состояния объекта в какой-либо момент времени.
Динамические модели отображают поведение объекта во времени.
Дискретные модели отображают поведение систем с дискретными состояниями.
Непрерывные модели представляют системы с непрерывными процессами.
Дискретно-непрерывные модели строятся тогда, когда исследователя интересуют оба эти типа процессов.
Очевидно, конкретная модель может быть стохастической, статической, дискретной или какой-либо другой, в соответствии со связями, показанными на рис. 1.1.
Сборник тестов (стр. 5 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 |
34. Что понимается под совокупными трудовыми затратами?
а) затраты живого и овеществленного сельскохозяйственного труда, заключенного в продукте
б) затраты живого и овеществленного труда, заключенного в продукте
35. Какое соотношение должно складываться между ростом производительности и оплаты труда?
а) темпы роста оплаты труда выше темпов роста производительности
б) темпы роста оплаты труда и производительности труда одинаковы
в) темпы роста производительности труда выше темпов роста оплаты
5. Тестовые задания по дисциплинам
«Экономико-математические методы и модели» и «Модельные программы предприятий АПК»
1. Укажите верное на ваш взгляд определение.
Экономико-математическая модель это:
а) система чисел характеризующих особенности функционирования экономических объектов или явлений;
б) концентрированные выражения существенных экономических взаимосвязей и закономерностей процесса функционирования экономической системы в математической форме;
в) математическое выражение отражающее существенные характеристики экономических явлений или процессов.
2. Сколько этапов содержит процесс моделирования?
3. Какие группы неизвестных величин может содержать экономико-математическая модель?
а) основные, дополнительные и косвенные;
б) основные, вспомогательные и косвенные;
в) основные, дополнительные и вспомогательные.
4. Критерий оптимальности это:
а) экономическая категория, характеризующая цель решения задачи;
б) математическое выражение, описывающее целевую функцию;
в) экономический показатель, характеризующий особенности функционирования экономики.
5. Критерий оптимальности при построении модели формализуется в виде:
а) ограничений задачи;
6. Экономико-математическая модель описывает:
а) все особенности функционирования объекта;
б) только наиболее существенные;
в) лишь незначительную часть.
7. В перечень условных обозначений при разработке структурной экономико-математической модели входят:
а) индексация, неизвестные и известные величины;
б) неизвестные и известные величины;
в) только индексация.
8. Ограничения задачи подразделяются на:
а) основные и дополнительные;
б) основные, дополнительные и вспомогательные;
в) главные и второстепенные.
9. Какие модели характеризуют индивидуальные особенности моделируемого объекта?
а) структурные и развёрнутые;
10. При использовании условных обозначений необходимо соблюдать принцип:
а) значимости, экономичности и запоминаемости;
б) значимости, последовательности, экономичности;
в) последовательности, экономичности и запоминаемости
11. Корреляционная модель это:
а) Математическое выражение типа уравнения, которое показывает, на сколько единиц изменяется результативный показатель при изменении факторного показателя на единицу;
б) система, формирующая взаимодействия результативных и факторных показателей экономического развития;
в) математическая форма, определяющая взаимозаменяемость ресурсов в процессе производства или распределения продукции.
12. Перед Вами формула, используемая для нахождения ошибки ассиметрии. Какое число необходимо подставить вместо,,х’’?
14. Перед Вами система уравнений для нахождения параметров корреляционной модели вида:
Какое выражение необходимо подставить в выделенном месте?
а)
б)
в)
15. Какая из перечисленных ниже зависимостей носит название Кобба-Дугласа?
а) 
б) 
в) 
16. Коэффициент парной корреляции изменяется:
17. Коэффициент множественной корреляции изменяется:
18. Критерий Фишера используется:
а) для оценки параметров корреляционные модели (КМ)
б) для оценки тесноты связи результативного и факторных признаков
в) для определения, насколько полно КМ выражает изучаемую закономерность
19. Правило «трех сигм» используется:
а) для оценки параметров корреляционной модели;
б) для нахождения ошибок в исходной информации;
в) для определения объема выборки
20. Скользящая переменная это:
а) добавка к минимальной границе скармливания отдельных видов кормов, вводимая на всё поголовье половозрастной группы животных, за счёт которой норма скармливания изменяется от минимума до максимума;
б) добавка корма к минимальной границе в расчете на единицу поголовья, в результате чего норма скармливания может изменяться до минимальной границы;
в) дополнительные корма для всего поголовья, за счет которых обеспечивается полноценное кормление животных в научно-обоснованных пропорциях
21. Чем отличаются ограничения по балансу основных кормов и побочных кормов?
а) содержанием правой части ограничения;
б) содержанием правой части и знаком ограничения;
в) знаком ограничения;
22. Содержит ли задача по оптимизации использования кормов в стойловый период ограничения:
а) по балансу кормов;
б) по использованию сельскохозяйственных угодий;
г) ограничения на скользящие переменные
23. Устойчивые количественные тенденции развития экономики выявляют с помощью:
а) оптимизационных моделей;
б) корреляционных моделей,
в) оптимизационных и корреляционных моделей.
24. На основе законов теории вероятностей строятся:
а) структурные модели;
в) стохастические модели;
г) детерминистические модели.
25. Форму связи результативного и факторных признаков в корреляционных моделях выбираем с использование следующих подходов:
а) имперического, графического и аналитического;
б) имперического, статистического и аналитического;
в) графического и логического;
г) графического и аналитического.
26. Цель решения задачи выражается количественно конкретным показателем называемым:
а) целевой функцией;
б) критерием оптимальности;
27. Основным свойством целевой функции является:
28. При построение модели оптимизации рационов кормления необходимо учитывать условия:
а) физиологические, производственные, территориальные;
б) экономические, производственные, территориальные;
в) физиологические, экономические, производственные;
г) физиологические, экономические, территориальные.
29. Использование «канадского» критерия оптимальности при оптимизации рационов кормления предусматривает:
а) минимизацию стоимости кормов рациона;
б) максимизацию условного чистого дохода;
в) максимизацию выхода продукции от скармливания кормов;
г) минимизацию кормовой площади для получения кормов рациона.
30. Скользящие переменные при комплексном внесении элементов питания минеральных удобрений используются:
а) для упрощения математической записи задачи;
б) для отражения особенностей внесения сложных удобрений;
в) для расчета дополнительного эффекта.
6. Тестовые задания по дисциплине
1. Сегментация рынка это…
а) Деление рынка на части (сегменты)
б) Классификация потенциальных потребителей в зависимости от особенностей спроса
в) Обеспечение адресности производимому товару
2. В сегментацию рынка по демографическим признакам включаются следующие критерии:
в) Численность населения
з) Чувствительность к цене
к) Эмоциональное отношение к товару
л) Уровень образования
м) Административное деление по регионам
3. Сколько этапов в процессе выбора целевого рынка?
а) Нет деления на этапы
4. Этот метод поиска оптимального числа сегментов предполагает последовательную поисковую работу. Метод не отличается быстротой, но и не требует существенных затрат. Укажите этот метод
5. Товарная стратегия предприятия это…
а) Создание нескольких разновидностей одного и того же товара
б) Выбор наиболее привлекательного для потребителей товара и концентрация на его производстве
в) Разработка направлений оптимизации товарной номенклатуры и определение наиболее оптимального ассортимента товаров
г) Создание новых или улучшенных товаров с целью максимизации прибыли предприятия.
7. Какие действия предприятия позволяют продлить жизненный цикл товара?
а) Новая рекламная компания
б) Повышение качества товара
г) Разработка принципиально нового товара
д) Выход на новый рынок
8. Модификация маркетинговых средств – это…
Понятие модели и моделирования
Сам по себе процесс моделирования в полной мере не формализован, большая роль в этом принадлежит опыту инженера. Но, тем не менее, рассматриваемый в теме процесс создания модели в виде шести этапов может стать основой для начинающих и с накоплением опыта может быть индивидуализирован.
1.1. Общее определение модели
Однако во многих случаях натурный эксперимент невозможен.
Например, наиболее полную оценку новому виду вооружения и способам его применения может дать война. Но не будет ли это слишком поздно?
Натурный эксперимент с новой конструкцией самолета может вызвать гибель экипажа.
Натурное исследование нового лекарства опасно для жизни человека.
Натурный эксперимент с элементами космических станций также может вызвать гибель людей.
Время подготовки натурного эксперимента и проведение мероприятий по обеспечению безопасности часто значительно превосходят время самого эксперимента. Многие испытания, близкие к граничным условиям, могут протекать настолько бурно, что возможны аварии и разрушения части или всего объекта.
Из сказанного следует, что натурный эксперимент необходим, но в то же время невозможен либо нецелесообразен.
Выход из этого противоречия есть и называется он » моделирование «.
Моделирование, в-третьих, это перенос полученных на модели сведений на оригинал или, иначе, приписывание свойств модели оригиналу. Чтобы такой перенос был оправдан, между моделью и оригиналом должно быть сходство, подобие.
Остановимся на основных целях моделирования.
Часто модель создается для применения в качестве средства обучения: модели-тренажеры, стенды, учения, деловые игры и т. п.
Гениальный полководец А. В. Суворов перед атакой крепости Измаил тренировал солдат на модели измаильской крепостной стены, построенной специально в тылу.
Наш знаменитый механик-самоучка И. П. Кулибин (1735-1818) создал модель одноарочного деревянного моста через р. Неву, а также ряд металлических моделей мостов. Они были полностью технически обоснованы и получили высокую оценку российскими академиками Л. Эйлером и Д. Бернулли. К сожалению, ни один из этих мостов не был построен.
1.2. Классификация моделей и моделирования
Каждая модель создается для конкретной цели и, следовательно, уникальна. Однако наличие общих черт позволяет сгруппировать все их многообразие в отдельные классы, что облегчает их разработку и изучение. В теории рассматривается много признаков классификации, и их количество не установилось. Тем не менее, наиболее актуальны следующие признаки классификации:
1.2.1. Классификация моделей и моделирования по признаку «характер моделируемой стороны объекта»
В соответствии с этим признаком модели могут быть:
Функциональные модели отображают только поведение, функцию моделируемого объекта. В этом случае моделируемый объект рассматривается как «черный ящик», имеющий входы и выходы. Физическая сущность объекта, природа протекающих в нем процессов, структура объекта остаются вне внимания исследователя, хотя бы потому, что неизвестны. При функциональном моделировании эксперимент состоит в наблюдении за выходом моделируемого объекта при искусственном или естественном изменении входных воздействий. По этим данным и строится модель поведения в виде некоторой математической функции.
1.2.2. Классификация моделей и моделирования по признаку «характер процессов, протекающих в объекте»
По этому признаку модели могут быть детерминированными или стохастическими, статическими или динамическими, дискретными или непрерывными или дискретно-непрерывными.
Детерминированные модели отображают процессы, в которых отсутствуют случайные воздействия.
Стохастические модели отображают вероятностные процессы и события.
Статические модели служат для описания состояния объекта в какой-либо момент времени.
Динамические модели отображают поведение объекта во времени.
Дискретные модели отображают поведение систем с дискретными состояниями.
Непрерывные модели представляют системы с непрерывными процессами.
Дискретно-непрерывные модели строятся тогда, когда исследователя интересуют оба эти типа процессов.
Очевидно, конкретная модель может быть стохастической, статической, дискретной или какой-либо другой, в соответствии со связями, показанными на рис. 1.1.
Понятие модели и моделирования
1.2.3. Классификация моделей и моделирования по признаку «способ реализации модели»
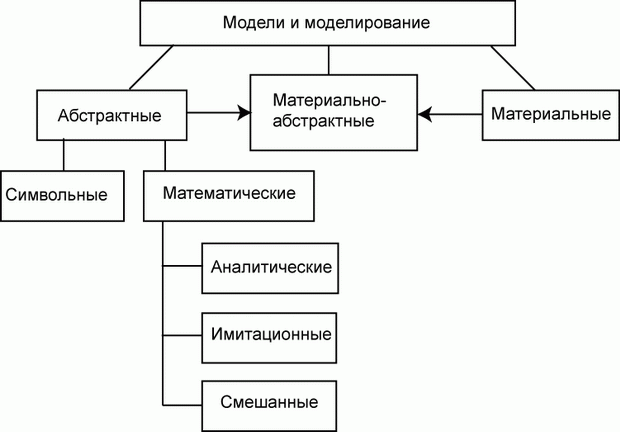
Согласно этому признаку модели делятся на два обширных класса:
Нередко в практике моделирования присутствуют смешанные, абстрактно-материальные модели.
Абстрактные модели представляют собой определенные конструкции из общепринятых знаков на бумаге или другом материальном носителе или в виде компьютерной программы.
Абстрактные модели, не вдаваясь в излишнюю детализацию, можно разделить на:
Символическая модель может иметь самостоятельное значение, но, как правило, ее построение является начальным этапом любого другого моделирования.
Математические модели могут быть:
Преобразование математических моделей по известным законам и правилам можно рассматривать как эксперименты. Решение на основе аналитических моделей может быть получено в результате однократного просчета безотносительно к конкретным значениям характеристик («в общем виде»). Это наглядно и удобно для выявления закономерностей. Однако для сложных систем построить аналитическую модель, достаточно полно отражающую реальный процесс, удается не всегда. Тем не менее, есть процессы, например, марковские, актуальность моделирования которых аналитическими моделями доказана практикой.
В чем заключается отличие имитационных и аналитических моделей?
В случае аналитического моделирования ЭВМ является мощным калькулятором, арифмометром. Аналитическая модель решается на ЭВМ.
Имитационные модели достаточно просто учитывают влияние случайных факторов. Для аналитических моделей это серьезная проблема. При наличии случайных факторов необходимые характеристики моделируемых процессов получаются многократными прогонами (реализациями) имитационной модели и дальнейшей статистической обработкой накопленной информации. Поэтому часто имитационное моделирование процессов со случайными факторами называют статистическим моделированием.
Если исследование объекта затруднено использованием только аналитического или имитационного моделирования, то применяют смешанное (комбинированное), аналитико-имитационное моделирование. При построении таких моделей процессы функционирования объекта декомпозируются на составляющие подпроцессы, и для которых, возможно, используют аналитические модели, а для остальных подпроцессов строят имитационные модели.
1.3. Этапы моделирования
Первый этап: уяснение целей моделирования. Вообще-то это главный этап любой деятельности. Цель существенным образом определяет содержание остальных этапов моделирования. Заметим, что различие между простой системой и сложной порождается не столько их сущностью, но и целями, которые ставит исследователь.
Обычно целями моделирования являются:
Третий этап: выбор языка программирования или моделирования, разработка алгоритма и программы модели. Модель может быть аналитической или имитационной, или их сочетанием. В случае аналитической модели исследователь должен владеть методами решения.
В истории математики (а это, впрочем, и есть история математического моделирования) есть много примеров тому, когда необходимость моделирования разного рода процессов приводила к новым открытиям. Например, необходимость моделирования движения привела к открытию и разработке дифференциального исчисления (Лейбниц и Ньютон) и соответствующих методов решения. Проблемы аналитического моделирования остойчивости кораблей привели академика Крылова А. Н. к созданию теории приближенных вычислений и аналоговой вычислительной машины.
Четвертый этап: планирование эксперимента. Математическая модель является объектом эксперимента. Эксперимент должен быть в максимально возможной степени информативным, удовлетворять ограничениям, обеспечивать получение данных с необходимой точностью и достоверностью. Существует теория планирования эксперимента, нужные нам элементы этой теории мы изучим в соответствующем месте дисциплины.
Пятый этап: выполнение эксперимента с моделью. Если модель аналитическая, то эксперимент сводится к выполнению расчетов при варьируемых исходных данных. При имитационном моделировании модель реализуется на ЭВМ с фиксацией и последующей обработкой получаемых данных. Эксперименты проводятся в соответствии с планом, который может быть включен в алгоритм модели. В современных системах моделирования такая возможность есть.
На этом рассмотрение последовательности моделирования закончим, сделав весьма важный вывод о необходимости документирования результатов каждого этапа. Это необходимо в силу следующих причин.
Во-первых, моделирование процесс итеративный, то есть с каждого этапа может осуществляться возврат на любой из предыдущих этапов для уточнения информации, необходимой на этом этапе, а документация может сохранить результаты, полученные на предыдущей итерации.
Во-вторых, в случае исследования сложной системы в нем участвуют большие коллективы разработчиков, причем различные этапы выполняются различными коллективами. Поэтому результаты, полученные на каждом этапе, должны быть переносимы на последующие этапы, то есть иметь унифицированную форму представления и понятное другим заинтересованным специалистам содержание.