какие наименьшие размеры выраженные целым числом сантиметров должен иметь прямоугольный лист бумаги
Ответы к странице 158 №767-774 ГДЗ к учебнику «Математика» 6 класс Мерзляк, Полонский, Якир
Ответы к параграфу 26. Цилиндр, конус, шар
Задание 767
Приведите примеры предметов, имеющих форму:
1) цилиндра;
2) конуса;
3) шара.
2) Колпак, морковь, стаканчик мороженого, пожарное ведро.
3) Яблоко, мяч, мыльный пузырь.
Задание 768
На рисунке 65 изображен цилиндр. Укажите:
1) образующую цилиндра;
2) радиус нижнего основания цилиндра;
3) радиус верхнего основания цилиндра.
2) OA − радиус нижнего основания цилиндра
3) O1B − радиус верхнего основания цилиндра
Задание 769
Радиус основания цилиндра равен 6 см, а его образующая − 8 см. Найдите площадь боковой поверхности цилиндра.
Задание 770
Найдите площадь боковой поверхности цилиндра, развертка которого изображена на рисунке 66 (длины отрезков даны в сантиметрах).
Задание 771
На рисунке 67 изображен конус. Укажите:
1) вершину конуса;
2) центр его основания;
3) образующую конуса;
4) радиус основания конуса;
5) высоту конуса.
2) O − центр основания конуса
3) MK − образующая конуса
4) OK − радиус основания конуса
5) OM − высота конуса
Задание 772
Радиус шара равен 6 см. Вычислите площадь сечения шара плоскостью, проходящей через центр шара.
Задание 773
Длина окружности, ограничивающей сечение шара плоскостью, проходящей через его центр, равна 12,56 см. Чему равен радиус шара?
Задание 774
Какие наименьшие размеры, выраженные целым числом сантиметров, должен иметь прямоугольный лист бумаги, чтобы им можно было обклеить боковую поверхность цилиндра с радиусом основания 5 см и высотой, равной диаметру основания?
Решение №2211 Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
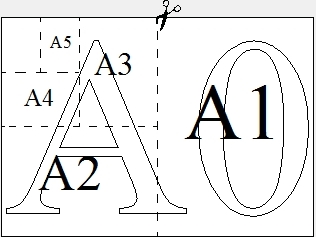
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2. И так далее. Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2. И так далее.
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
Источник: ОГЭ Ященко 2022 (50 вариантов)
Задание 1
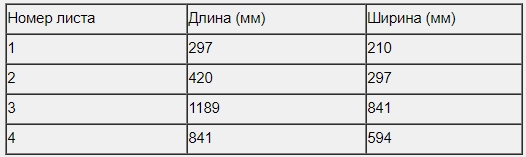
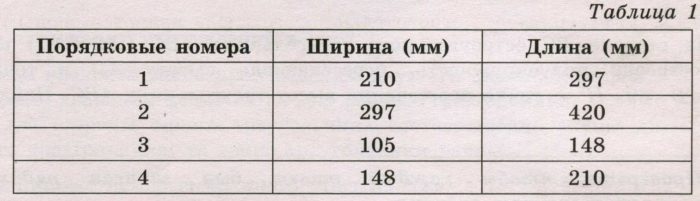
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Решение
Чем больше число стоит у буквы А, тем формат бумаги меньше по размеру, т.к. его больше раз разрезали.
Формат А4 – самый маленький, А3 – соседний к А4, больше А4 по одной из сторон в два раза.
А0 – самый большой, А1 – соседний к А0, меньше А0 по одной из сторон в два раза. Соотносим размеры из таблицы:
Ответ: 3421.
Задание 2
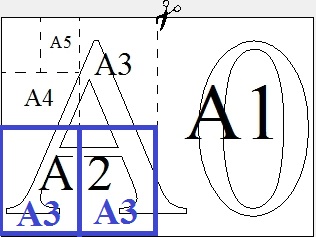
Сколько листов формата А3 получится из одного листа формата А2?
Решение
Из листа А2 получится 2 листа А3.
Ответ: 2.
Задание 3
Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.
Решение
Из первого задания знаем, что лист А1 имеет размеры 841 мм на 594 мм.
Переведём стороны в см (1см = 10 мм):
841 мм = 84,1 см
594 мм = 59,4 см
Найдём площадь листа А1:
SA1 = 84,1·59,4 = 4995,54 см 2
Ответ: 4995,54.
Задание 4
Найдите отношение большей стороны листа формата А2 к меньшей. Ответ округлите до десятых.
Решение
Лист А2 в два раза меньше листа А1 по большей стороне листа А1.
Лист А1 имеет размеры 841 мм на 594 мм. Найдём размеры сторон листа А2:
841/2 = 420,5 мм
594 мм
Найдём отношение большей стороны к меньшей стороне, округлив до десятых:
Ответ: 1,4.
Задание 5
Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.
Решение:
Способ 1
Лист А5 в два раза меньше листа А4 по большей стороне листа А4.
Лист А4 имеет размеры 297 мм на 210 мм (знаем из 1-го задания). Найдём размеры сторон листа А5:
297/2 = 148,5 мм
210 мм
Переведём стороны в метры (1 м = 100·10 = 1000 мм):
148,5 мм = 0,1485 м
210 мм = 0,210 = 0,21 м
Найдём площадь листа А5 в кв. м:
0,1485·0,21 = 0,031185 м 2
Найдём площадь 500 таких листов:
0,031185·500 = 15,5925 м 2
1 м 2 = 80 г, найдём массу пачки бумаги в граммах:
15,5925·80 = 1247,4 г
Но в ответах сборника подразумевают, что нужно решать Способом 2 :
Тогда площадь 500 листов А5 равна:
500/32 = 15,625 м 2
1 м 2 = 80 г, масса пачки листов равна:
Какие наименьшие размеры выраженные целым числом сантиметров должен иметь прямоугольный лист бумаги
Найдите ширину листа бумаги формата А0. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.
Установите соответствие между форматами и номерами листов. В ответ запишите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
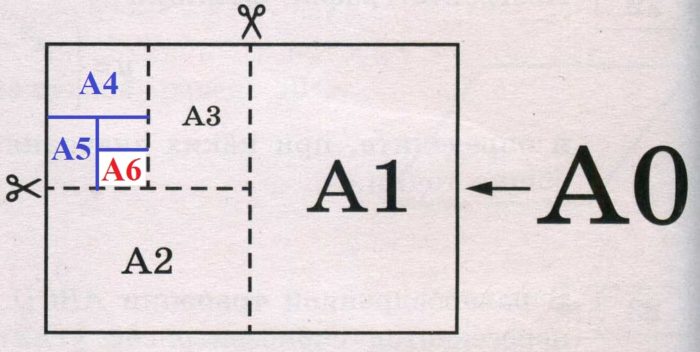
Пользуясь рисунком, можно сделать вывод, что формату А0 соответствует лист 3, формату А1 — лист 4, фомату А3 — лист 2, формату А4 — лист 1.
Сколько листов формата А3 получится из одного листа формата А2?
Исходя из рисунка, можно сделать вывод, что 2 листа формата А3 получится из одного листа формата А2.
Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.
Лист формата А1 является прямоугольником со сторонами 84,1 см и 59,4 см, поэтому его площадь равна
Приведём другое решение.
Примечание Дмитрия Гущина.
Нам неизвестно, какой ответ считают верным авторы задачи. В действительности точного ответа на вопрос задачи и вовсе нет, поскольку искомая площадь может быть найдена только приближенно. Разработчикам ОГЭ следовало бы уточнить формулировку этого задания, например, дав указание «Ответ дайте в квадратных сантиметрах, округлите до тысяч».
Решение №931 Общепринятые форматы листов бумаги обозначают буквой А и цифрой …
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Если лист формата А0 разрезать пополам, получаются два листа формата А1. Если лист А1 разрезать пополам, получаются два листа формата А2 и так далее.
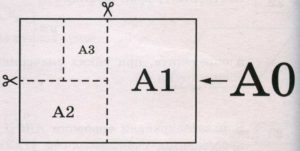
Отношение длины листа к его ширине у всех форматов, обозначенных буквой А, должно быть одно и то же, то есть листы должны быть подобны друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится). На практике размеры листа округляются до целого числа миллиметров.
В таблице 1 даны размеры листов бумаги четырёх форматов: от А3 до А6.
Задание 1
Для листов бумаги форматов А6, А5, А4 и А3 определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
Решение
Чем больше число стоит у буквы А, тем формат бумаги меньше по размеру, т.к. его больше раз разрезали.
Формат А6 – самый маленький, А3 – самый большой. Выбираем из Таблицы 1, размеры по возрастанию:
Ответ: 3412.
Задание 2
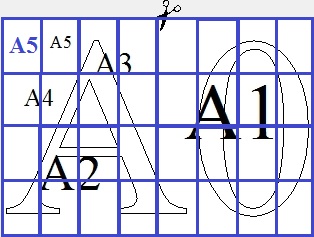
Сколько листов бумаги формата А6 получится при разрезании одного листа бумаги формата А0?
Решение
Дорежем начальный лист до А6 :
Можно посчитать по рисунку, или выразить:
A0 = 2· A1
A1 = 2· A2
A2 = 2· A3
A3 = 2· A4
A4 = 2· A5
A5 = 2· A6
Подставляем всё в A0:
A0 = 2·2·2·2·2·2·A6 = 64· A6
Из листа А0 получим 64 листа A6.
Ответ: 64.
Задание 3
Найдите длину меньшей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
Решение
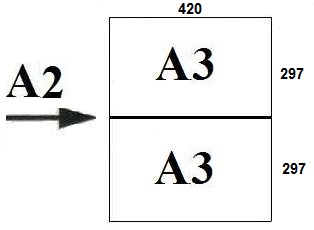
Из таблицы 1, знаем размер А3, а А2 это два листа А3, соединённых большей стороной:
Тогда у А2 стороны 420 и 297+297 = 594. Меньшая из них равна 420.
Ответ: 420.
Задание 4
Найдите площадь листа бумаги формата А5. Ответ дайте в квадратных сантиметрах.
Решение
Из таблицы 1, знаем размер А5:
Ширина = 148 мм
Длина = 210 мм
Площадь листа равна:
148·210 = 31080 мм 2
Переведём в см 2 :
1 см = 10 мм
1см 2 = 10·10 = 100 мм 2
31080/100 = 310,8 см 2
Ответ: 310,8.
Задание 5
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 10 пунктов на листе формата А4? Размер шрифта округляется до целого.
Решение:
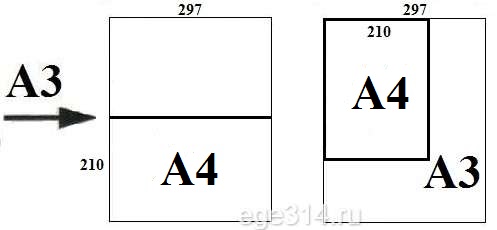
Из таблицы 1 знаем размеры A3 и A4. Перевернём лист А4 в положение в котором будем печатать на нём.
Сторона листа А3 больше стороны листа А4 в:
297/210 ≈ 1,414 раза
Тогда и шрифт на А3 будет во столько же раз больше:
1,414·10 = 14,14 ≈ 14 пунктов
Ответ: 14.
Задание 6*
Решение:
Лист формата А3 имеет размеры:
Ширина = 297 мм = 0,297 м
Длина = 420 мм = 0,420 м
Площадь одного такого листа:
0,297·0,420 = 0,12474 м 2
Площадь 250 таких листов:
0,12474·250 = 31,185 м 2
Какие наименьшие размеры выраженные целым числом сантиметров должен иметь прямоугольный лист бумаги
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А3, А5 и А6.
| Номер листа | Длина (мм) | Ширина (мм) |
|---|---|---|
| 1 | 210 | 148 |
| 2 | 594 | 420 |
| 3 | 148 | 105 |
| 4 | 420 | 297 |
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.
Установите соответствие между форматами и номерами листов. В ответ запишите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
Пользуясь рисунком, можно сделать вывод, что формату А0 соответствует лист 3, формату А1 — лист 4, фомату А3 — лист 2, формату А4 — лист 1.
Сколько листов формата А3 получится из одного листа формата А2?
Исходя из рисунка, можно сделать вывод, что 2 листа формата А3 получится из одного листа формата А2.
Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.
Лист формата А1 является прямоугольником со сторонами 84,1 см и 59,4 см, поэтому его площадь равна
Приведём другое решение.
Примечание Дмитрия Гущина.
Нам неизвестно, какой ответ считают верным авторы задачи. В действительности точного ответа на вопрос задачи и вовсе нет, поскольку искомая площадь может быть найдена только приближенно. Разработчикам ОГЭ следовало бы уточнить формулировку этого задания, например, дав указание «Ответ дайте в квадратных сантиметрах, округлите до тысяч».