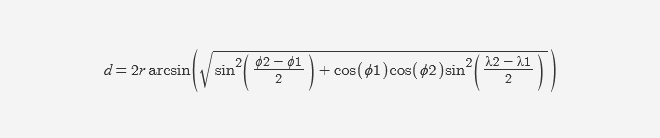php расстояние между точками php
Рассчитываем расстояние между двумя точками на поверхности Земли на PHP/JavaScript
Представим, что в вашем распоряжении две пары географических координат (долгота и широта), и ваша задача – рассчитать кратчайшее расстояние между ними. Что для этого нужно сделать и, соответственно, учесть?
Поскольку Земля имеет форму, приближенную к сфере, расстояние между двумя географическими объектами на ней мы будем искать по формуле Гаверсинуса, которая в преобразованном виде выглядит следующим образом:
r – радиус Земли в километрах;
φ1, φ2 – широта в радианах;
λ1, λ2 – долгота в радианах;
На основе ее составим две (по одной из указанных языков программирования) несложные функции, которые помогут нам получить нужный результат.
Как рассчитать расстояние между двумя координатами на PHP?
Итак, формула у нас есть, просто переведем ее в код и для удобства упакуем в некую функцию.
Вид всего этого будет следующий:
В нем мы (в виде широта_1, долгота_1, широта_2, долгота_2) передаем известные координаты объектов и получаем кратчайшее расстояние между ними.
Поскольку Земля – не идеальная сфера, значение радиуса мы берем усредненное – 6371 километр, а потому в итоговом результате будет присутствовать погрешность в 0.5% (если верить Википедии).
Все координаты перед началом расчета мы переводим из градусов в радианы через функцию deg2rad.
Последовательность передаваемых пар координат не имеет значения.
Как рассчитать расстояние между двумя координатами на JavaScript?
Предыдущий вариант из PHP по определению расстояния между двумя точками в JavaScript будет выглядеть следующим образом:
Согласитесь, не такая уж и сложная, но определенно полезная функция.
Измерение расстояния между двумя координатами в PHP
Привет, мне нужно рассчитать расстояние между двумя точками, имеющими широту и долготу.
Я бы не хотел обращаться к внешнему API.
Я попытался реализовать формулу Хаверсина в PHP:
Тестируя это с некоторыми заданными точками, которые имеют общедоступные расстояния, я не получаю надежного результата.
Я не понимаю, есть ли ошибка в исходной формуле или в моей реализации
12 ответов
Не так давно я написал пример формулы гаверсина и опубликовал его на своем сайте:
Как правильно указал TreyA, формула Хаверсина имеет слабые места с противоположными точками из-за ошибок округления (хотя она стабильно на малых расстояниях). Чтобы их обойти, вы можете использовать вместо них формулу Винсенти.
Один из самых простых способов:
Он будет округлен до 2 десятичных знаков.
Множитель изменяется в каждой координате из-за теории расстояния большого круга, как написано здесь:
И вы можете вычислить ближайшее значение, используя эту формулу, описанную здесь:
Здравствуйте, здесь Код для определения расстояния и времени с использованием двух разных широт и долготы
Для точных значений сделайте это так:
Попробуйте эту функцию, чтобы вычислить расстояние между точками широты и долготы.
Затем используйте функцию как
Надеюсь, это поможет
Попробуйте, это дает потрясающие результаты
Довольно старый вопрос, но для тех, кто интересуется кодом PHP, который возвращает те же результаты, что и Google Maps, следующее выполняет свою работу:
Я тестировал с разными координатами, и он отлично работает.
Я думаю, что это должно быть быстрее, чем некоторые альтернативы. Но не проверял.
Подсказка: Google Maps использует 6378137 в качестве радиуса Земли. Так что использование его с другими алгоритмами тоже может сработать.
Для тех, кто любит короче и быстрее (не вызывая deg2rad ()).
Измерение расстояния между двумя координатами в PHP
Привет, мне нужно рассчитать расстояние между двумя точками, имеющими lat и long.
Я хотел бы избежать любого вызова внешнего API.
Я попытался реализовать Формулу Хаверсина в PHP:
Испытывая это с некоторыми заданными точками, которые имеют общественные расстояния, я не получаю надежный результат.
Я не понимаю, есть ли ошибка в исходной формуле или в моей реализации
Недавно я написал пример формулы haversine и опубликовал ее на своем веб-сайте:
Как правильно указал TreyA, формула Хаверсина имеет слабости с антиподальными точками из-за ошибок округления (хотя она устойчива на малых расстояниях). Чтобы обойти их, вы могли бы использовать формулу Винченти.
Я нашел этот код, который дает мне надежные результаты.
Вот результаты теста:
Здесь простой и совершенный код для вычисления расстояния между двумя широтами и долготой. Ниже приведен следующий код: http://www.codexworld.com/distance-between-two-addresses-google-maps-api-php/
Для тех, кто любит короче и быстрее (не вызывая deg2rad ()).
Для точных значений сделайте так:
Хм, я думаю, это должно сделать это …
Осмелюсь … Я забыл деградировать все значения в круг-функциях …
Попробуйте это дает потрясающие результаты
Множитель изменяется при каждой координате из-за большой теории расстояния круга, как написано здесь:
и вы можете рассчитать ближайшее значение, используя следующую формулу:
ключ преобразует каждую градус – минута – второе значение во все значения градуса:
Привет здесь Код для получения расстояния и времени с использованием двух разных латов и длинных
Вы можете проверить, что Example Below Link получает время между двумя разными местоположениями, используя широту и долготу в php
Расчет времени маршрута по координатам с использованием open street maps. язык PHP
Если расстояние между двумя точками слишком маленькое, то возвращается длинна маршрута и время нулями. Подскажите что делать?
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Как подключить географические карты типа Google Maps или Open street maps в своё приложение
Всем доброго времени суток. Вопрос такой: как подключить географические карты типа Google Maps или.
Google Maps API. Расчет времени и расстояния пути. За сколько сделаете?
Здравствуйте. Пытался разобраться в Google api, но не очень получилось, да. Вообщем, кто может.
Open street map
Здравствуйте! Подскажите, пожалуйста, в каком приложении можно работать с osm, если нужно.
Расчет скорости автомобиля по GPS-координатам и времени их получения
Добрый день! Может кто реализовывал эту функцию на SQL, поделитесь пожалуйста.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Open Street Map navigation
Добрый день. возникла необходимость сделать в приложении прокладку маршрута по oms картам, третий.
Прорисовка маршрута на google maps
Здравствуйте. На форме подключил гугл мапс через библиотеку Gmap.dll сделал метки, как прорисовать.
Google maps, построение маршрута между двумя точками
кто может поделиться рабочим примером построения маршрута между двумя точками для android studio?
Расчет расстояний между городами по их координатам
Расчет расстояний между точками по их координатам на плоскости элементарен, на поверхности Земли — немного посложнее: мы рассмотрим измерение расстояния и начального азимута между точками без проекционных преобразований.
Для начала разберемся в терминологии.
Введение
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения.
Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут отличен от постоянного, следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.
Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или π*R, где R – радиус сферы.
На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.
Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.
Формулы
Существует три способа расчета сферического расстояния большого круга.
1. Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением.
φ1, λ1; φ2, λ2 — широта и долгота двух точек в радианах
Δλ — разница координат по долготе
Δδ — угловая разница
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
2. Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
3. Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.