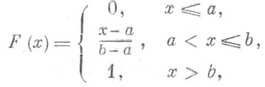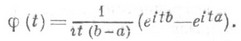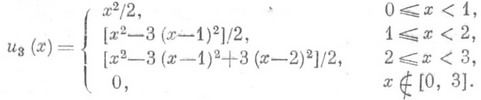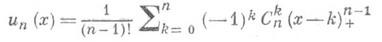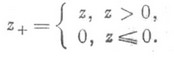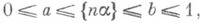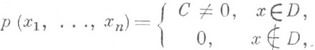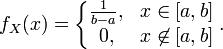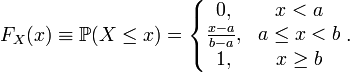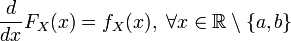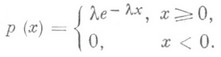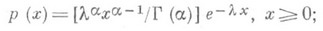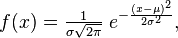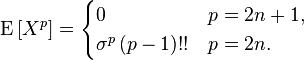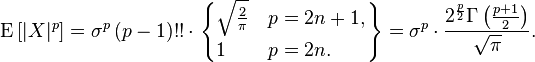Сколько параметров имеет равномерное распределение
Сколько параметров имеет равномерное распределение
13.5.3 тБЧОПНЕТОПЕ ТБУРТЕДЕМЕОЙЕ
оБ РТБЛФЙЛЕ ЬФП ТБУРТЕДЕМЕОЙЕ ЧУФТЕЮБЕФУС ФПЗДБ, ЛПЗДБ УТЕДЙ РТЙОЙНБЕНЩИ УМХЮБКОЩНЙ ЧЕМЙЮЙОБНЙ ЪОБЮЕОЙК ОЕФ ЛБЛЙИ МЙВП РТЕДРПЮФЙФЕМШОЩИ. ч ЮБУФОПУФЙ, ПВЩЮОП УЮЙФБАФ, ЮФП УПВЩФЙС, РТПЙУИПДСЭЙЕ Ч РТПЙЪЧПМШОЩЕ НПНЕОФЩ ЧТЕНЕОЙ У ТБЧОПК ЧЕТПСФОПУФША НПЗХФ РТПЙУИПДЙФШ Ч МАВПК НПНЕОФ ЧТЕНЕОЙ.
 |  |
| тЙУ 1. | тЙУ 2. |
оБКДЕН ЪОБЮЕОЙЕ РПУФПСООПК у ЙЪ ХУМПЧЙС, ЮФП РМПЭБДШ, ПЗТБОЙЮЕООБС ЛТЙЧПК ТБУРТЕДЕМЕОЙС, ТБЧОБ ЕДЙОЙГЕ.

пФУАДБ 
оБКДЕН ЧЩТБЦЕОЙЕ ЖХОЛГЙЙ ТБУРТЕДЕМЕОЙС F(И) ДМС ТБЧОПНЕТОПЗП ЪБЛПОБ ТБУРТЕДЕМЕОЙС
фБЛЙН ПВТБЪПН, ЙНЕЕН
зТБЖЙЛ ЖХОЛГЙЙ F(x) ЙЪПВТБЦЕО ОБ ТЙУХОЛЕ 2.
пРТЕДЕМЙН ПУОПЧОЩЕ ЮЙУМПЧЩЕ ИБТБЛФЕТЙУФЙЛЙ УМХЮБКОПК ЧЕМЙЮЙОЩ и, ЙНЕАЭЕК ТБЧОПНЕТОПЕ ТБУРТЕДЕМЕОЙЕ.

йФБЛ, НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ ТБЧОПНЕТОПЗП ТБУРТЕДЕМЕОЙС ОБИПДЙФУС РПУЕТЕДЙОЕ ЙОФЕТЧБМБ 

нПДЩ ТБЧОПНЕТОПЕ ТБУРТЕДЕМЕОЙЕ ОЕ ЙНЕЕФ.
дЙУРЕТУЙА УМХЮБКОПК ЧЕМЙЮЙОЩ и ОБИПДЙН РП ЖПТНХМЕ
фП ЕУФШ 

чЕТПСФОПУФШ РПРБДБОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ и, ЙНЕАЭЕК ТБЧОПНЕТОПЕ ТБУРТЕДЕМЕОЙЕ, ОБ ПФТЕЪПЛ 

Равномерное распределение непрерывной случайной величины
Равномерное распределение, плотность вероятности, функция распределения равномерно распределённой случайной величины
Равномерным распределением непрерывной случайной величины называется распределение, в котором значения случайной величины с двух сторон ограничены и в границах интервала имеют одинаковую вероятность. Это означает, что в в данном интервале плотность вероятности постоянна.
Таким образом, при равномерном распределении плотность вероятности имеет вид
Значения f(x) в крайних точках a и b участка (a, b) не указываются, так как вероятность попадания в любую из этих точек для непрерывной случайной величины равна нулю.
Кривая равномерного распределения имеет вид прямоугольника, опирающегося на участок (a, b) (рисунок ниже), в связи с чем равномерное распределение иногда называют «прямоугольным».
Эта вероятность находится по формуле
и геометрически представляет собой площадь, дважды заштрихованную на рисунке ниже и опирающуюся на часть (α, β) участка (a, b) :
Функция распределения F(x) непрерывной случайной величины при равномерном распределении имеет вид
Характеристики равномерного распределения
Характеристики равномерного распределения:
Решение примеров на равномерное распределение
Пример 1. Наблюдения показали, что вес ящика, предназначенного для транспортировки овощей, является равномерно распределённой случайной величиной в интервале от 985 г. до 1025 г. Случайно выбран один ящик. Найти характеристики равномерно распределённой случаной величины при условиях, которые будут указаны в решении.
Решение. Найдём вероятность того, что вес данного ящика будет в интервале от 995 г. до 1005 г. :

Найдём среднее значение непрерывной случайной величины:

Найдём стандартное отклонение:

Определим, у скольки процентов ящиков вес находится на удалении одного стандартного отклонения от среднего значения (т. е. в интервале 

Решение. Найдём плотность распределения f(x) :
Найдём математическое ожидание случайной величины:
Найдём вероятность того, что пассажиру придётся ждать поезда не больше полминуты:
Решение. Найдём стандартное отклонение:
Непрерывное равномерное распределение
Связанные понятия
Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
В математике и физике, выборка по уровням это разновидность выборки методом случайных блужданий, основывающаяся на том факте что для выборки функции с заданным распределением достаточно производить равномерноую выборку из области под графиком плотности вероятности.
Случайная перестановка — это случайное упорядочение множества объектов, то есть случайная величина, элементарными событиями которой являются перестановки. Использование случайных перестановок зачастую является базой в областях, использующих рандомизированные алгоритмы. К таким областям относятся теория кодирования, криптография и моделирование. Хорошим примером случайной перестановки является тасование колоды карт.
В теории вероятностей и статистике, о наборе случайных величин говорят, что они являются независимыми (и) одинаково распределёнными, если каждая из них имеет такое же распределение, что и другие, и все величины являются независимыми в совокупности. Фраза «независимые одинаково распределённые» часто сокращается аббревиатурой i.i.d. (от англ. independent and identically-distributed), иногда — «н.о.р».
Не путать с «симплекс-методом» — методом оптимизации произвольной функции. См. Метод Нелдера — МидаСимплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве.
Главным образом, интерес к вопросу распространения волн в случайно-неоднородных средах (какой является, например, атмосфера) можно объяснить бурным развитием спутниковых технологий. В этом случае становится важной задача расчета характеристик (например, амплитуды) волны прошедшей через среду и установления их связей с параметром неоднородности среды. Важную роль здесь и играет функция Грина для случайно-неоднородной среды, зная которую можно определить эти характеристики. Рассматривается прохождение.
РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ
Р. р. на отрезке числовой прямой (прямоугольное распределение). Р. р. на каком-либо отрезке [ а, b], а 2 /12. Функция распределения задается формулой
( Х n являются цифрами в двоичном разложении X). Случайное число Xимеет Р. р. на отрезке [0,1]. Этот факт имеет важные статистич. приложения, см., напр., Случайные и псевдослучайные числа.
для 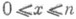

Распределение суммы 
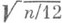
P.p. на отрезке как предельное распределение. Ниже приводятся типичные примеры возникновения Р. р. на [0,1] в качестве предельного.
2) Пусть параметры 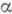
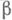

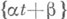
3) Р. р. встречается как предельное распределение дробных долей нек-рых функций g(n) натурального аргумента п. Напр., при иррациональном a. доля тех 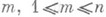
имеет пределом при 
Р. р. на под множествах 

где Собратна k-мерному объему (или лебеговой мере) области D.
Рассматривают также и Р. р. на поверхностях. Так, «случайное направление» (напр., в 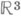
Роль Р. р. на алгебраич. группах играет нормированная Хаара мера.
Лит.:[1] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 2, М., 1967.
Смотреть что такое «РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ» в других словарях:
Равномерное распределение — Равномерное распределение: Дискретное равномерное распределение; Непрерывное равномерное распределение … Википедия
РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ — (прямоугольное распределение) распределение вероятностей случайной величины Х, принимающей значение из интервала (а h, a + h) с постоянной плотностью вероятности … Большой Энциклопедический словарь
РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ — (uniform distribution) Частота (frequency) распределения, при которой переменная равновероятно принимает любое значение между известными пределами. Если переменная х лежит между нижним пределом а и верхним пределом b, при равномерном… … Экономический словарь
равномерное распределение — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN even distribution … Справочник технического переводчика
равномерное распределение — 1.36. равномерное распределение; прямоугольное распределение а) Распределение вероятностей непрерывной случайной величины, плотность распределения вероятности которой постоянна на конечном интервале [а, b] и равна нулю вне его. b) Распределение… … Словарь-справочник терминов нормативно-технической документации
равномерное распределение — (прямоугольное распределение), распределение вероятностей случайной величины X, принимающей значение из интервала (а h, а+h) с постоянной плотностью вероятности: * * * РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ (прямоугольное… … Энциклопедический словарь
РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ — (прямоугольное распределение), распределение вероятностей случайной величины X, принимающей значение из интервала (a h, a+h) с пост. плотностью вероятности … Естествознание. Энциклопедический словарь
равномерное распределение — tolygusis skirstinys statusas T sritis fizika atitikmenys: angl. uniform distribution vok. gleichförmige Verteilung, f rus. равномерное распределение, m pranc. loi rectangulaire, f; loi uniforme, f … Fizikos terminų žodynas
равномерное распределение — (1) Распределение вероятностей непрерывной случайной величины, плотность вероятности которой постоянна на конечном интервале [a,b] и равна нулю вне его. (2) Распределение вероятностей дискретной случайной величины X, такое что Pr
Равномерное распределение — прямоугольное распределение, специальный вид распределения вероятностей случайной величины Х, принимающей значения из интервала (а h, a + h); характеризуется плотностью вероятности (См. Плотность вероятности): … … Большая советская энциклопедия
Билет №22.Равномерное распределение.Параметры распределения,числовые характеристики



Интегрируя определённую выше плотность, получаем:
Так как плотность равномерного распределения разрывна в граничных точках отрезка [a,b]\!, то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:
Билет №23.Показательное распределение.Параметры распределения,числовые характеристики.
Показательное распределение-непрерывное распределение вероятностей случайной величины X, задаваемое плотностью
характеристич. функция: (1-it/l)-1.
П. р. входит в семейство распределений, называемых гамма-распределениями и задаваемых плотностью
Билет №24.Нормальное распределение.Параметры распределния,числовые хар-ки.Правило трех сигм,Стандартное нормальное распределение.Связь нормального распределения общего вида со стандартным норм распределением
Нормальное распределение,также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса:
где параметр μ — математическое ожидание, медиана и мода распределения, а параметр σ — стандартное отклонение (σ² — дисперсия) распределения.
Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в многомерном нормальном распределении.
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1.
Важное значение нормального распределения во многих областях науки, например, в математической статистике и статистической физике вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования.
Моментами и абсолютными моментами случайной величины X называются математические ожидания Xp и 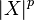
Если 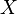
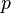
Здесь 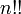
Центральные абсолютные моменты для неотрицательных целых p таковы:
Правило трёх сигм( 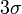
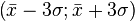
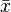
Если же истинная величина 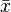
Билет №25.Закон больших чисел.Лемма о среднем арифметическом случайных величин.Теорема Бернулли.Центральная предельная теорема.
Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.
Всегда найдётся такое конечное число испытаний, при котором с любой заданной наперёд вероятностью меньше 1 относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.
Общий смысл закона больших чисел — совместное действие большого числа одинаковых и независимых случайных факторов приводит к результату, в пределе не зависящему от случая.
На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.