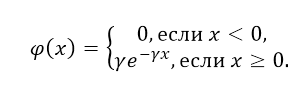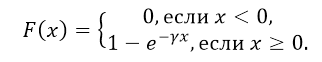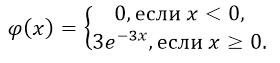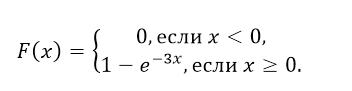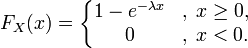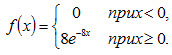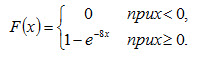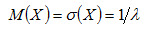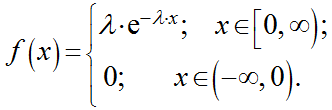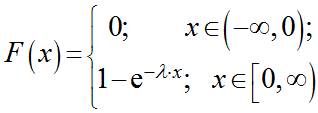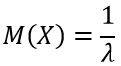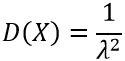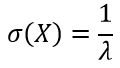Случайная величина имеет показательное распределение с параметром

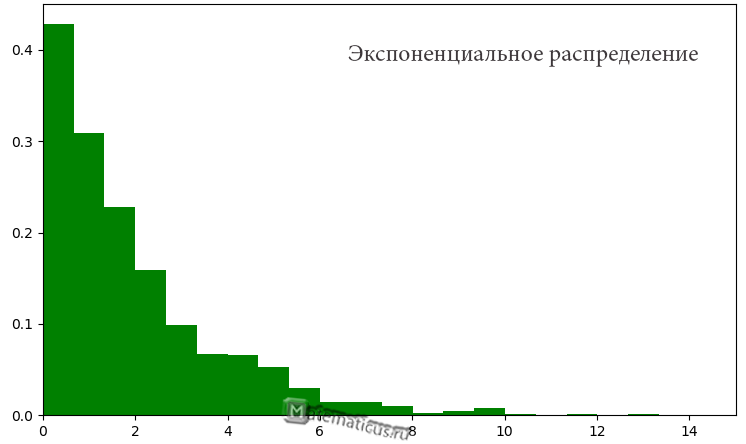
Показательное распределение

Вы будете перенаправлены на Автор24

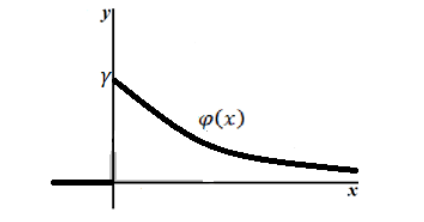
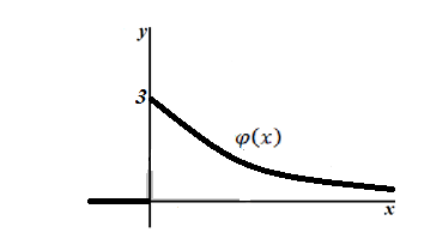
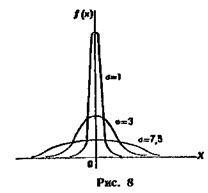
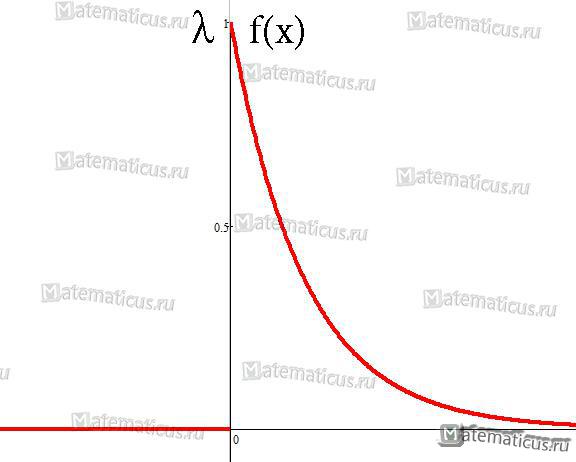
График плотности показательного распределения имеет вид (рис. 1):

Рисунок 2. График плотности показательного распределения.

Функция показательного распределения

Как нетрудно проверить, функция показательного распределения имеет вид:

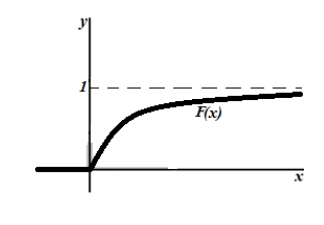
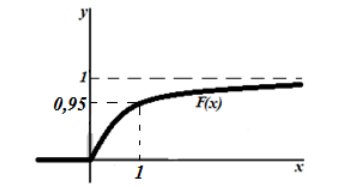
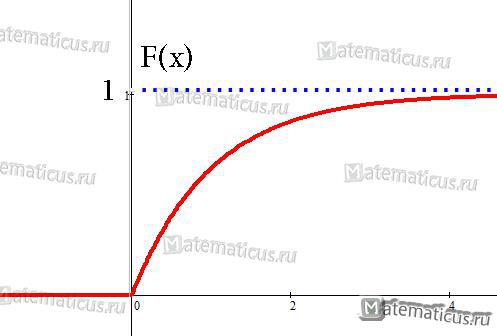
График функции показательного распределения имеет вид:

Рисунок 4. График функции показательного распределения.

Вероятность попадания случайной величины при показательном распределении

Пример задачи на показательное распределение

Найти плотность распределения и построить её график.

Найти функцию распределения и построить её график.

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение данного распределения.

Источник

Показательное распределение

Показательное распределение

Плотность вероятности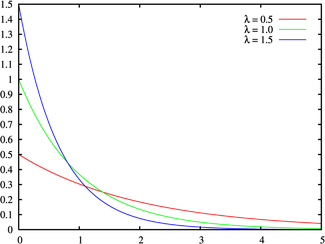
Функция распределения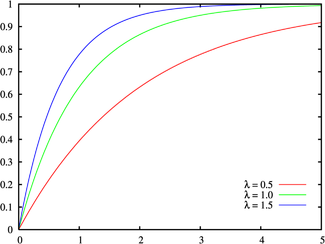
Параметры	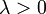— интенсивность или обратный коэффициент масштаба
Носитель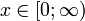
Плотность вероятности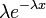
Функция распределения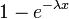
Математическое ожидание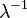
Медиана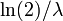
Мода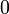
Дисперсия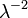
Коэффициент асимметрии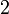
Коэффициент эксцесса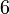
Информационная энтропия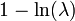
Производящая функция моментов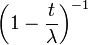
Характеристическая функция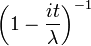

Показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Содержание

Определение

.

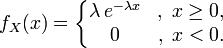
Иногда семейство экспоненциальных распределений параметризуют обратным параметром 1 / λ :

.

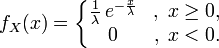
Оба способа одинаково естественны, и необходима лишь договорённость, какой из них используется.

В этой статье для определённости будем предполагать, что плотность экспоненциальной случайной величины X задана первым уравнением, и будем писать: .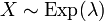

Функция распределения

Моменты

Несложным интегрированием находим, что производящая функция моментов для экспоненциального распределения имеет вид:

,

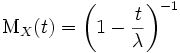
откуда получаем все моменты:

.

, .

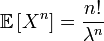
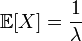
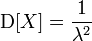
Отсутствие памяти

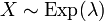
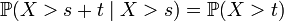
Пусть . Тогда .

Пример. Пусть автобусы приходят на остановку случайно, но с некоторой фиксированной средней интенсивностью. Тогда количество времени, уже затраченное пассажиром на ожидание автобуса, не влияет на время, которое ему ещё придётся прождать.

Связь с другими распределениями

Вероятностные распределения Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | Колмогорова | Коши | Лапласа | логнормальное | Лоренца | нормальное (Гаусса) | равномерное | Парето | Стьюдента | Фишера | хи-квадрат | экспоненциальное | Эрланга многомерное нормальное

править

Смотреть что такое «Показательное распределение» в других словарях:

показательное распределение — экспоненциальное распределение — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы экспоненциальное распределение EN exponential distribution … Справочник технического переводчика

Показательное распределение — распределение вероятностей на действительной прямой с плотностью вероятностей (См. Плотность вероятности) р (х), равной при х ≥ 0 показательной функции λe λx, λ > 0 [отсюда название П. р.] и при х … Большая советская энциклопедия

ОТРИЦАТЕЛЬНОЕ ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ — то же, что показательное распределение … Математическая энциклопедия

РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ — одно из основных понятий вероятностей теории и математической статистики. При современном подходе в качестве математич. модели изучаемого случайного явления берется соответствующее вероятностное пространство, где W множество элементарных … Математическая энциклопедия

Экспоненциальное распределение — Показательное распределение Плотность вероятности Функция распределения … Википедия

НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ — распределение вероятностей, не имеющее атомов. Если атомы суть отдельные точки, то Н. р. противоположно дискретному распределению (см. также Атомическое распределение). Вместе с дискретным распределением Н. р. образует основные типы распределений … Математическая энциклопедия

ЭРЛАНГА РАСПРЕДЕЛЕНИЕ — эрланговское распределение, сосредоточенное на распределение вероятностей с плотностью где целое и действительное параметры. Характеристич. функция Э. р. имеет вид а математич. ожидание и дисперсия соответственно и … Математическая энциклопедия

ЛАПЛАСА РАСПРЕДЕЛЕНИЕ — непрерывное распределение вероятностей с плотностью где параметр сдвига, а a>0, масштабный параметр. Плотность Л. р. симметрична относительно точки x=b, производная плотности имеет разрыв при x=b. Характеристич. функция Л. р. с параметрами a и … Математическая энциклопедия

ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ — то же, что показательное распределение … Математическая энциклопедия

Источник

Случайная величина имеет показательное распределение с параметром

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

. (4.14)

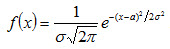
Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и σ (σ >0).

Нормированным называют нормальное распределение с параметрами а=0 и σ =1.

Плотность нормированного распределения

. (4.15)

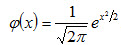
Эта функция табулирована (см. приложение 1).

Замечание 2. Функция F(x) общего нормального распределения

, (4.16)

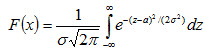
а функция нормированного распределения

. (4.17)

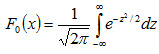
Функция F₀(x) табулирована. Легко проверить, что

.

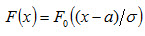
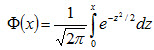
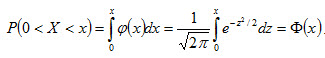
Замечание 3. Вероятность попадания нормированной нормальной величины Х в интервал (0, x) можно найти, пользуясь функцией Лапласа . Действительно,

.

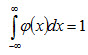
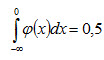
Замечание 4. Учитывая, что (свойство 2), и, следовательно, в силу симметрии φ(x) относительно нуля

, а значит, и P (-∞ 0 при х а.

Следовательно, при х = а функция имеет максимум равный .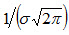

5. Разность х-а содержится в аналитическом выра­жении функции в квадрате, т. е. график функции симметричен относительно прямой х = а.

6. Исследуем функцию на точки перегиба. Найдем вторую производную:

.

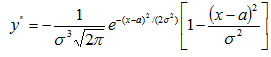
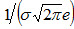
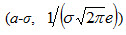
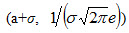
Легко видеть, что при х=а+σ и х=а— σ вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции равно ). Таким образом, точки графика (а-σ, ) и (а+σ, ) являются точками перегиба.

Как влияют на форму и расположение нормальной кривой значения параметров а и σ?

При а = 0 и σ = 1 нормальную кривую 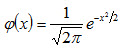называют нормированной.

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью

(4.20)

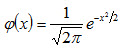
Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока (показательный закон надежности).

Функция распределения показательного закона:

(4.21)

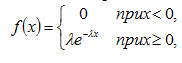
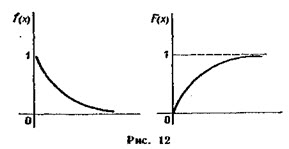
Графики плотности и функции распределения показательного закона:

Пример 1. Написать плотность и функцию распределения показательного закона, если параметр λ = 8.

Очевидно, искомая плотность распределения

Искомая функция распределения

Вероятность попадания в интервал (а, b) непрерывной случайной величины X, распределенной по показательному закону,

Пример 2. Непрерывная случайная величина X распределена по показательному закону

Числовые характеристики показательного распределения

Математическое ожидание показательного распределения равно обратной величине параметра λ:

. (4.23)

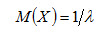
Дисперсия показательного распределения равна

. (4.24)

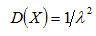
Среднее квадратическое отклонение показательного распределения равно

. (4.25)

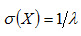
Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.

Пример 3. Непрерывная случайная величина X распределена по показательному закону

Источник

Равномерный и показательный законы распределения непрерывной случайной величины

Как было сказано ранее, примерами распределений вероятностей непрерывной случайной величины Х являются:

Дадим понятие равномерного и показательного законов распределения, формулы вероятности и числовые характеристики рассматриваемых функций.

Показатель	Раномерный закон распределения	Показательный закон распределения
Определение	Равномерным называется распределение вероятностей непрерывной случайной величины X, плотность которого сохраняет постоянное значение на отрезке [a;b] и имеет вид	Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью, имеющей вид
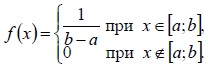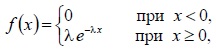		где λ – постоянная положительная величина
Функция распределения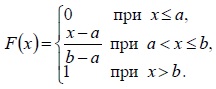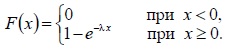
Вероятность попадания в интервал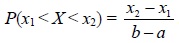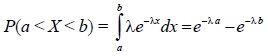
Математическое ожидание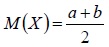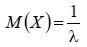
Дисперсия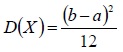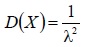
Среднее квадратическое отклонение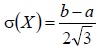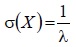

Примеры решения задач по теме «Равномерный и показательный законы распределения»

Задача 1.

Автобусы идут строго по расписанию. Интервал движения 7 мин. Найти: а) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее двух минут; б) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус не менее трех минут; в) математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания пассажира.

Решение. 1. По условию задачи непрерывная случайная величина X= <время ожидания пассажира>равномерно распределена между приходами двух автобусов. Длина интервала распределения случайной величины Х равна b-a=7, где a=0, b=7.

4. Находим для показательного распределения:

Другие статьи по данной теме:

Список использованных источников

2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна

Источник

Показательный (экспоненциальный) закон распределения

Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения, если её плотность вероятности имеет вид:

График плотности распределения случайной величины по показательному (экспоненциальному) закону

Функция распределения F(X) случайной величины X, распределенной по показательному закону, выражается формулой:

График функции распределения случайной величины по показательному (экспоненциальному) закону

λ — параметр распределения.

Математическое ожидание равно:

Дисперсия равна:

Среднеквадратическое отклонение (СКО) равно:

Вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a, b), находится по формуле:

P(a −λa −e −λb

Показательное распределение применяют в теории массового обслуживания и надёжности, для моделирования времени безотказной работы, длительности безаварийной работы приборов и машин, демографии и т. д. Пример, устройство после включения ломается через короткий промежуток времени.

Случайная величина X – время работы лампы накаливания. Случайная величина подчинена показательному распределению. Определить вероятность того, что время работы лампы накаливания будет не меньше 800 часов, если среднее время работы лампы накаливания 400 часов.

В соответствии с условием задачи, математическое ожидание M(x) случайной величины X равно 400 часам, отсюда следует, что

Подставляя в формулу выше, получаем вероятность

Источник