Согласно методу наименьших квадратов в качестве оценок параметров следует использовать
Согласно методу наименьших квадратов в качестве оценок параметров следует использовать
2.2. Оценка параметров линейной модели по методу наименьших квадратов (МНК)
Этот метод и многочисленные его модификации являются основными и в эконометрике. Поэтому при изучении данного курса ему нужно уделить особое внимание.
2.2.1. Критерий наименьших квадратов. Сравнение с другими возможными критериями
Запишем уравнение для отдельных наблюдений (реализаций) в парной линейной регрессии
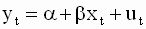 |
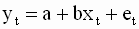 |
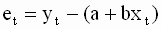 |
Уравнение ( 2.6 ) выражает эмпирическую взаимосвязь между переменными модели и его можно записать только относительно конкретных наблюдений. Подчеркнем, что ошибки модели являются наблюдаемыми величинами, поскольку их можно определить исходя из наблюдений переменных модели.
В методе наименьших квадратов оценки a и b параметров модели строятся так, что бы минимизировать сумму квадратов ошибок (остатков) модели по всем наблюдениям. Таким образом, критерий (целевая функция) наименьших квадратов записывается в виде
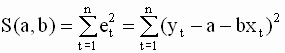 |
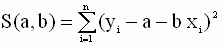 |
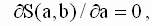 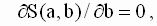 |
которую необходимо решить относительно переменных a и b. По правилам вычисления производных получим следующие выражения:
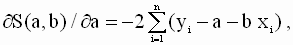 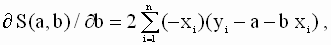 |
так что значения параметров a и b, минимизирующие квадратичную форму ( 2.8 ), удовлетворяют соотношениям
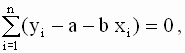 | ||||||||||||||||||||
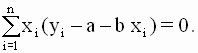 |
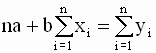 | ||||||||||||||||||
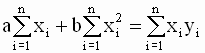 |
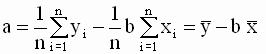 |
где 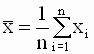
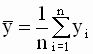
Подставив выражение для a во второе уравнение системы, получим
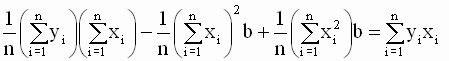 , , |
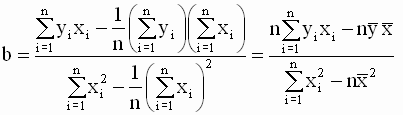 , , |
Таким образом, мы получили следующие соотношения для оценок параметров модели
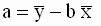 , , |
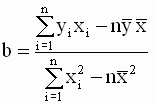 |
Однако, в теоретических исследованиях и практических расчетах чаще используют другую, более удобную эквивалентную форму записи уравнений для оценок. Эта форма получается, если использовать следующие соотношения
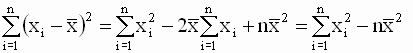 |
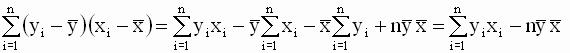 |
Эти соотношения позволяют получить новую форму записи выражения для b (в отклонениях от выборочных средних значений)
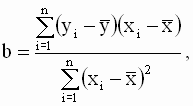 |
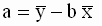 |
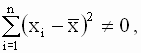 |
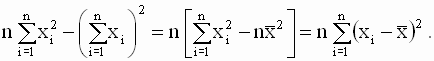 |
Выражение для коэффициента b часто записывают также, используя понятия выборочной вариации (дисперсии) и выборочной ковариации.
Выборочная вариация определяется соотношением вида
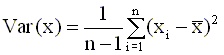 |
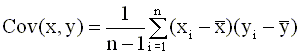 |
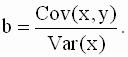 |
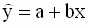 |
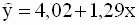 |
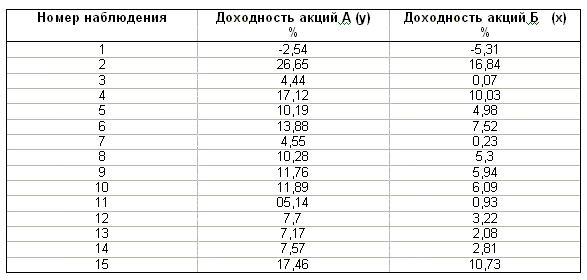
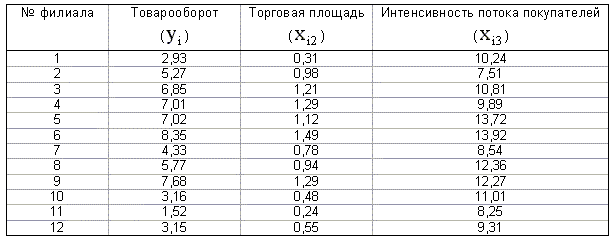
Торговое предприятие имеет несколько филиалов. Исследуем зависимость годового товарооборота отдельного филиала от: а) размера торговой площади; б) среднедневной интенсивности потока покупателей. Поскольку мы пока не умеем строить модели множественной регрессии, построим две «частные» модели парной регрессии.
Таблица 1.2
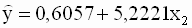 |
Для второй регрессии получаем следующие оценки: a=-2,0394, b=0,6846. Ее уравнение
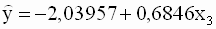 |
Дайте интерпретацию параметров регрессий примера 2.2.
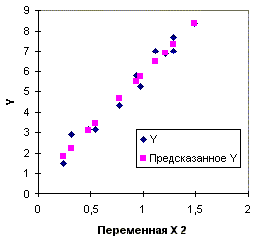
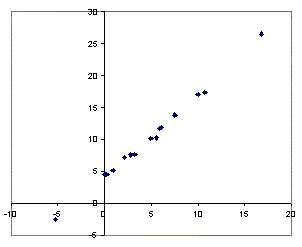
Рис.2.5а. Диаграмма рассеяния и линия
регрессии (первая модель, пример 2.2)
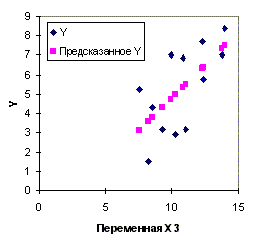
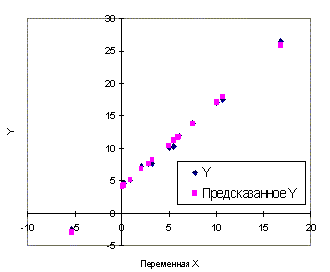
Рис.2.5б. Диаграмма рассеяния и линия
регрессии (вторая модель, пример 2.2)
Глава 3 Оценка параметров
Цель любого физического эксперимента — проверить, выполняется ли некоторая теоретическая закономерность ( модель ), а также получить или уточнить её параметры. Поскольку набор экспериментальных данных неизбежно ограничен, а каждое отдельное измерение имеет погрешность, можно говорить лишь об оценке этих параметров. В большинстве случаев измеряется не одна величина, а некоторая функциональная зависимость величин друг от друга. В таком случае возникает необходимость построить оценку параметров этой зависимости.
Для построения оценки нужны следующие компоненты
процедура построения оценки параметров по измеренным данным («оценщик»):
Рассмотрим самые распространенные способы построения оценки.
3.1 Метод минимума хи-квадрат
Обозначим отклонения результатов некоторой серии измерений от теоретической модели y = f ( x | θ ) как
где θ — некоторый параметр (или набор параметров), для которого требуется построить наилучшую оценку. Нормируем Δ y i на стандартные отклонения σ i и построим сумму
Можно показать (см. [ 5 ] ), что оценка по методу хи-квадрат является состоятельной, несмещенной и, если данные распределены нормально, имеет максимальную эффективность (см. приложение 5.2 ).
3.2 Метод максимального правдоподобия.
Рассмотрим кратко один из наиболее общих методов оценки параметров зависимостей — метод максимума правдоподобия.
Сделаем два ключевых предположения:
зависимость между измеряемыми величинами действительно может быть описана функцией y = f ( x | θ ) при некотором θ ;
все отклонения Δ y i результатов измерений от теоретической модели являются независимыми и имеют случайный (не систематический!) характер.
3.3 Метод наименьших квадратов (МНК).
Оценка по методу наименьших квадратов (МНК) удобна в том случае, когда не известны погрешности отдельных измерений. Однако тот факт, что метод МНК игнорирует информацию о погрешностях, является и его основным недостатком. В частности, это не позволяет определить точность оценки (например, погрешности коэффициентов прямой σ k и σ b ) без привлечения дополнительных предположений (см. п. 3.6.2 и 3.6.3 ).
3.4 Проверка качества аппроксимации
В теории вероятностей доказывается (см. [ 4 ] или [ 5 ] ), что ожидаемое среднее значение (математическое ожидание) суммы χ 2 в точности равно числу степеней свободы:
3.5 Оценка погрешности параметров
Легко убедиться, что:
Вероятностное содержание этого интервала будет равно 68% (его еще называют 1– σ интервалом). Отклонение χ 2 на 2 будет соответствовать уже 95% доверительному интервалу.
3.6 Методы построения наилучшей прямой
3.6.1 Метод наименьших квадратов
Пусть сумма квадратов расстояний от точек до прямой минимальна:
Данный метод построения наилучшей прямой называют методом наименьших квадратов (МНК).
Напомним, что угловые скобки означают усреднение по всем экспериментальным точкам:
Эти соотношения и есть решение задачи о построении наилучшей прямой методом наименьших квадратов.
3.6.2 Погрешность МНК в линейной модели
Пользуясь в этих предположениях формулами для погрешностей косвенных измерений (см. раздел ( 2.6 )) можно получить следующие соотношения:
В частном случае y = k x :
3.6.3 Недостатки и условия применимости МНК
Формулы ( 3.7 ) (или ( 3.6 )) позволяют провести прямую по любому набору экспериментальных данных, а полученные выше соотношения — вычислить соответствующую среднеквадратичную ошибку для её коэффициентов. Однако далеко не всегда результат будет иметь физический смысл. Перечислим ограничения применимости данного метода.
В первую очередь метод наименьших квадратов — статистический, и поэтому он предполагает использование достаточно большого количества экспериментальных точек (желательно 10″ display=»inline»> n > 10 ).
Наконец, стоит предостеречь от использования любых аналитических методов «вслепую», без построения графиков. В частности, МНК не способен выявить такие «аномалии», как отклонения от линейной зависимости, немонотонность, случайные всплески и т.п. Все эти случаи требуют особого рассмотрения и могут быть легко обнаружены визуально при построении графика.
3.6.4 Метод хи-квадрат построения прямой
Пусть справедливы те же предположения, что и для метода наименьших квадратов, но погрешности σ i экспериментальных точек различны. Метод минимума хи-квадрат сводится к минимизации суммы квадратов отклонений, где каждое слагаемое взято с весом w i = 1 / σ i 2 :
Этот метод также называют взвешенным методом наименьших квадратов.
Определим взвешенное среднее от некоторого набора значений < x i >как
где W = ∑ i w i — нормировочная константа.
Повторяя процедуру, использованную при выводе ( 3.7 ), нетрудно получить (получите) совершенно аналогичные формулы для искомых коэффициентов:
Математика на пальцах: методы наименьших квадратов
Я математик-программист. Самый большой скачок в своей карьере я совершил, когда научился говорить:«Я ничего не понимаю!» Сейчас мне не стыдно сказать светилу науки, что мне читает лекцию, что я не понимаю, о чём оно, светило, мне говорит. И это очень сложно. Да, признаться в своём неведении сложно и стыдно. Кому понравится признаваться в том, что он не знает азов чего-то-там. В силу своей профессии я должен присутствовать на большом количестве презентаций и лекций, где, признаюсь, в подавляющем большинстве случаев мне хочется спать, потому что я ничего не понимаю. А не понимаю я потому, что огромная проблема текущей ситуации в науке кроется в математике. Она предполагает, что все слушатели знакомы с абсолютно всеми областями математики (что абсурдно). Признаться в том, что вы не знаете, что такое производная (о том, что это — чуть позже) — стыдно.
Но я научился говорить, что я не знаю, что такое умножение. Да, я не знаю, что такое подалгебра над алгеброй Ли. Да, я не знаю, зачем нужны в жизни квадратные уравнения. К слову, если вы уверены, что вы знаете, то нам есть над чем поговорить! Математика — это серия фокусов. Математики стараются запутать и запугать публику; там, где нет замешательства, нет репутации, нет авторитета. Да, это престижно говорить как можно более абстрактным языком, что есть по себе полная чушь.
Знаете ли вы, что такое производная? Вероятнее всего вы мне скажете про предел разностного отношения. На первом курсе матмеха СПбГУ Виктор Петрович Хавин мне определил производную как коэффициент первого члена ряда Тейлора функции в точке (это была отдельная гимнастика, чтобы определить ряд Тейлора без производных). Я долго смеялся над таким определением, покуда в итоге не понял, о чём оно. Производная не что иное, как просто мера того, насколько функция, которую мы дифференцируем, похожа на функцию y=x, y=x^2, y=x^3.
Я сейчас имею честь читать лекции студентам, которые боятся математики. Если вы боитесь математики — нам с вами по пути. Как только вы пытаетесь прочитать какой-то текст, и вам кажется, что он чрезмерно сложен, то знайте, что он хреново написан. Я утверждаю, что нет ни одной области математики, о которой нельзя говорить «на пальцах», не теряя при этом точности.
Задача на ближайшее время: я поручил своим студентам понять, что такое линейно-квадратичный регулятор. Не постесняйтесь, потратьте три минуты своей жизни, сходите по ссылке. Если вы ничего не поняли, то нам с вами по пути. Я (профессиональный математик-программист) тоже ничего не понял. И я уверяю, в этом можно разобраться «на пальцах». На данный момент я не знаю, что это такое, но я уверяю, что мы сумеем разобраться.
Итак, первая лекция, которую я собираюсь прочитать своим студентам после того, как они в ужасе прибегут ко мне со словами, что линейно-квадратичный регулятор — это страшная бяка, которую никогда в жизни не осилить, это методы наименьших квадратов. Умеете ли вы решать линейные уравнения? Если вы читаете этот текст, то скорее всего нет.
Итак, даны две точки (x0, y0), (x1, y1), например, (1,1) и (3,2), задача найти уравнение прямой, проходящей через эти две точки:
Эта прямая должна иметь уравнение типа следующего:
Здесь альфа и бета нам неизвестны, но известны две точки этой прямой:
Можно записать это уравнение в матричном виде:
Тут следует сделать лирическое отступление: что такое матрица? Матрица это не что иное, как двумерный массив. Это способ хранения данных, более никаких значений ему придавать не стоит. Это зависит от нас, как именно интерпретировать некую матрицу. Периодически я буду её интерпретировать как линейное отображение, периодически как квадратичную форму, а ещё иногда просто как набор векторов. Это всё будет уточнено в контексте.
Давайте заменим конкретные матрицы на их символьное представление:
Тогда (alpha, beta) может быть легко найдено:
Более конкретно для наших предыдущих данных:
Что ведёт к следующему уравнению прямой, проходящей через точки (1,1) и (3,2):
Окей, тут всё понятно. А давайте найдём уравнение прямой, проходящей через три точки: (x0,y0), (x1,y1) и (x2,y2):
Ой-ой-ой, а ведь у нас три уравнения на две неизвестных! Стандартный математик скажет, что решения не существует. А что скажет программист? А он для начала перепишет предыдующую систему уравнений в следующем виде:
И дальше постарается найти решение, которое меньше всего отклонится от заданных равенств. Давайте назовём вектор (x0,x1,x2) вектором i, (1,1,1) вектором j, а (y0,y1,y2) вектором b:
В нашем случае векторы i,j,b трёхмерны, следовательно, (в общем случае) решения этой системы не существует. Любой вектор (alpha\*i + beta\*j) лежит в плоскости, натянутой на векторы (i, j). Если b не принадлежит этой плоскости, то решения не существует (равенства в уравнении не достичь). Что делать? Давайте искать компромисс. Давайте обозначим через e(alpha, beta) насколько именно мы не достигли равенства:
И будем стараться минимизировать эту ошибку:
Очевидно, что ошибка минимизируется, когда вектор e ортогонален плоскости, натянутой на векторы i и j.
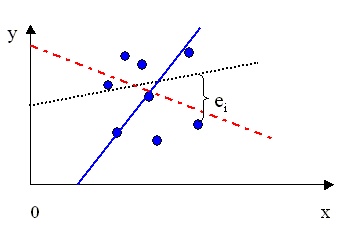
Иными словами: мы ищем такую прямую, что сумма квадратов длин расстояний от всех точек до этой прямой минимальна:
UPDATE: тут у меня косяк, расстояние до прямой должно измеряться по вертикали, а не ортогональной проекцией. Вот этот комментатор прав.
Совсеми иными словами (осторожно, плохо формализовано, но на пальцах должно быть ясно): мы берём все возможные прямые между всеми парами точек и ищем среднюю прямую между всеми:
Иное объяснение на пальцах: мы прикрепляем пружинку между всеми точками данных (тут у нас три) и прямой, что мы ищем, и прямая равновесного состояния есть именно то, что мы ищем.
Минимум квадратичной формы
Итак, имея данный вектор b и плоскость, натянутую на столбцы-векторы матрицы A (в данном случае (x0,x1,x2) и (1,1,1)), мы ищем вектор e с минимум квадрата длины. Очевидно, что минимум достижим только для вектора e, ортогонального плоскости, натянутой на столбцы-векторы матрицы A:
Иначе говоря, мы ищем такой вектор x=(alpha, beta), что:
Напоминаю, что этот вектор x=(alpha, beta) является минимумом квадратичной функции ||e(alpha, beta)||^2:
Тут нелишним будет вспомнить, что матрицу можно интерпретирвать в том числе как и квадратичную форму, например, единичная матрица ((1,0),(0,1)) может быть интерпретирована как функция x^2 + y^2:
Вся эта гимнастика известна под именем линейной регрессии.
Уравнение Лапласа с граничным условием Дирихле
Теперь простейшая реальная задача: имеется некая триангулированная поверхность, необходимо её сгладить. Например, давайте загрузим модель моего лица:
Изначальный коммит доступен здесь. Для минимизации внешних зависимостей я взял код своего софтверного рендерера, уже подробно описанного на хабре. Для решения линейной системы я пользуюсь OpenNL, это отличный солвер, который, правда, очень сложно установить: нужно скопировать два файла (.h+.c) в папку с вашим проектом. Всё сглаживание делается следующим кодом:
X, Y и Z координаты отделимы, я их сглаживаю по отдельности. То есть, я решаю три системы линейных уравнений, каждое имеет количество переменных равным количеству вершин в моей модели. Первые n строк матрицы A имеют только одну единицу на строку, а первые n строк вектора b имеют оригинальные координаты модели. То есть, я привязываю по пружинке между новым положением вершины и старым положением вершины — новые не должны слишком далеко уходить от старых.
Ещё раз: переменными являются все вершины, причём они не могут далеко отходить от изначального положения, но при этом стараются стать похожими друг на друга.
Всё бы было хорошо, модель действительно сглажена, но она отошла от своего изначального края. Давайте чуть-чуть изменим код:
В нашей матрице A я для вершин, что находятся на краю, добавляю не строку из разряда v_i = verts[i][d], а 1000*v_i = 1000*verts[i][d]. Что это меняет? А меняет это нашу квадратичную форму ошибки. Теперь единичное отклонение от вершины на краю будет стоить не одну единицу, как раньше, а 1000*1000 единиц. То есть, мы повесили более сильную пружинку на крайние вершины, решение предпочтёт сильнее растянуть другие. Вот результат:
Давайте вдвое усилим пружинки между вершинами:
Логично, что поверхность стала более гладкой:
А теперь ещё в сто раз сильнее:
Что это? Представьте, что мы обмакнули проволочное кольцо в мыльную воду. В итоге образовавшаяся мыльная плёнка будет стараться иметь наименьшую кривизну, насколько это возможно, касаясь-таки границы — нашего проволочного кольца. Именно это мы и получили, зафиксировав границу и попросив получить гладкую поверхность внутри. Поздравляю вас, мы только что решили уравнение Лапласа с граничными условиями Дирихле. Круто звучит? А на деле всего-навсего одну систему линейных уравнений решить.
Уравнение Пуассона
Давайте ещё крутое имя вспомним.
Предположим, что у меня есть такая картинка:
Всем хороша, только стул мне не нравится.
Разрежу картинку пополам: 
И выделю руками стул:
Затем всё, что белое в маске, притяну к левой части картинки, а заодно по всей картинке скажу, что разница между двумя соседними пикселями должна равняться разнице между двумя соседними пикселями правой картинки:
Код и картинки доступны здесь.
Пример из жизни
Я специально не стал делать вылизанные результаты, т.к. мне хотелось всего-навсего показать, как именно можно применять методы наименьших квадратов, это обучающий код. Давайте я теперь дам пример из жизни:
У меня есть некоторое количество фотографий образцов ткани типа вот такой:
Моя задача сделать бесшовные текстуры из фотографий вот такого качества. Для начала я (автоматически) ищу повторяющийся паттерн:
Если я вырежу прямо вот этот четырёхугольник, то из-за искажений у меня края не сойдутся, вот пример четыре раза повторённого паттерна:
Вот фрагмент, где чётко видно шов:
Поэтому я вырезать буду не по ровной линии, вот линия разреза:
А вот повторённый четыре раза паттерн:
И его фрагмент, чтобы было виднее:
Уже лучше, рез шёл не по прямой линии, обойдя всякие завитушки, но всё же шов виден из-за неравномерности освещения на оригинальной фотографии. Вот тут-то и приходит на помощь метод наименьших квадратов для уравнения Пуассона. Вот конечный результат после выравнивания освещения:
Текстура получилась отлично бесшовной, и всё это автоматически из фотографии весьма посредственного качества. Не бойтесь математики, ищите простые объяснения, и будет вам инженерное счастье.
- Современный php новые возможности и передовой опыт джош локхарт
- Согласно параметрам безопасности интернета один или несколько файлов потенциально опасны windows 10
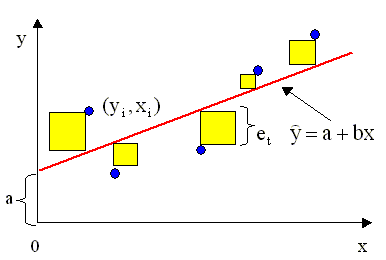
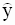 зависимой переменной y уравнением
зависимой переменной y уравнением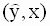 . Эмпирический коэффициент b является частной производной ( 2.19 ) по независимой переменной x (регрессору). Следовательно можно дать следующую интерпретацию коэффициента b: изменение величины независимой переменной x на единицу при фиксированном значении параметра a приведет к изменению оценки переменной y на величину коэффициента b.
. Эмпирический коэффициент b является частной производной ( 2.19 ) по независимой переменной x (регрессору). Следовательно можно дать следующую интерпретацию коэффициента b: изменение величины независимой переменной x на единицу при фиксированном значении параметра a приведет к изменению оценки переменной y на величину коэффициента b.